10 Principles of Reliable Data Transport Part 2

10. Principles of Reliable Data Transport – Part 2 n n Basic concepts Stop-and-wait protocol Go-Back-N protocol Selective Repeat protocol Roch Guerin (with adaptations from Jon Turner and John De. Hart, and material from Kurose and Ross)

Improving RDT 3. 0 n Basic goal is to be able to transmit non-stop under normal (no errors) operation » first ack must arrive before the sender finishes transmission of Nth packet n To enable more efficient operation, we want a protocol that can keep transmitting while waiting for acks, i. e. , one that pipelines transmissions » sender can transmit up to N packets while waiting for acks • each packet labeled with sequence # from set of S>N sequence #s » receiver sends acks with sequence numbers n Two major variants » go-back-N (cumulative ack) and selective repeat (specific ack) 2
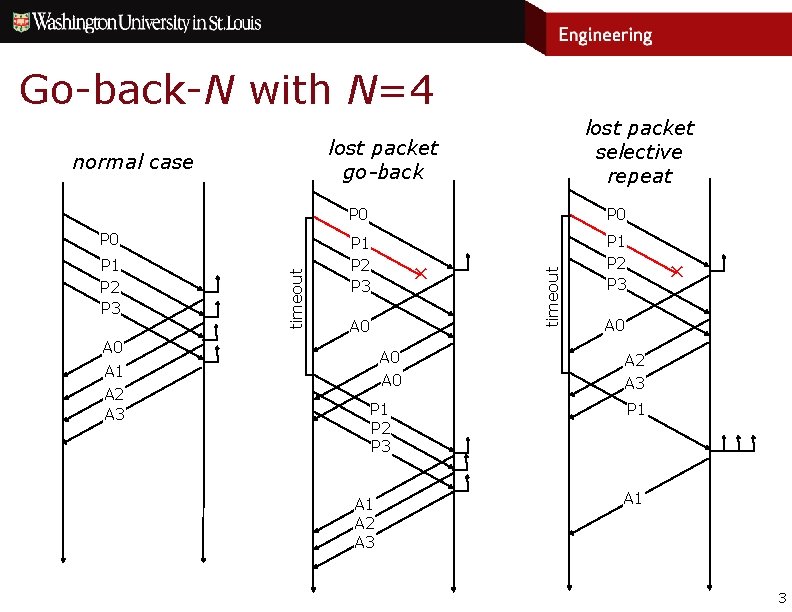
Go-back-N with N=4 lost packet go-back timeout P 0 P 0 P 1 P 2 P 3 A 0 A 1 A 2 A 3 ✕ A 0 P 1 P 2 P 3 A 1 A 2 A 3 timeout normal case P 1 P 2 P 3 lost packet selective repeat ✕ A 0 A 2 A 3 P 1 A 1 3

Go-Back-N Operation Sender variables Receiver variables » Send window size: SWS=N » Last pkt sent: LPS » Last ack received: LAR n Allow pkt transmissions as long as LPS-LAR ≤ SWS » Receive window size: RWS (= 1) » Last pkt received: LPR » Latest acceptable pkt: LAP n » i. e. , LAP = RWS +LPR (RWS=1 only one acceptable pkt) » If LPS-LAR ≤ SWS, send next pkt with SN = LPS+1 n ACK for pkt number X>LAR updates LAR to X (slides the window) » Note that X ≠ LAR+1 is OK (cumulative ACKs acknowledge all pkts up to X) Need: LAP-LPR ≤ RWS n When pkt SN arrives (with RWS=1) » If SN !=LPR+1, discard pkt • Only accepts packets in order » Else accept pkt and set LPR = SN » Send (cumulative) ACK for LPR • It is a cumulative ACK but it is always just 1 more than last ACK sent! 4
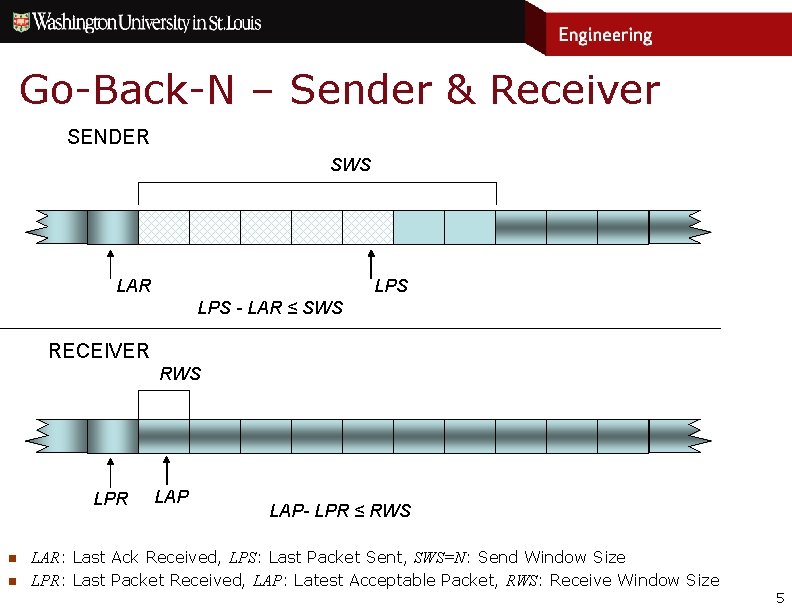
Go-Back-N – Sender & Receiver SENDER SWS LAR LPS - LAR ≤ SWS RECEIVER RWS LPR n n LAP- LPR ≤ RWS LAR: Last Ack Received, LPS: Last Packet Sent, SWS=N: Send Window Size LPR: Last Packet Received, LAP: Latest Acceptable Packet, RWS: Receive Window Size 5

Buffering & Numbering Packets Sender 7 0 n 1 2 6 5 4 3 copies of n unacked packets ready to send 4 n n Protocol uses sequence numbers 0…S– 1=2 m-1 Re-use sequence numbers in circular fashion » all sequence number arithmetic is modulo S n Window size SWS specifies number of pkts that can be unacknowledged n How big should S be? Obviously) S ≥ SWS » Suppose S=4 (Seq. Num. field {0, …, 3}) and SWS = 4 • Sender transmit frames 0, …, 3 • Arrive successfully, but all ACKs are lost • Sender retransmits 0, …, 3 (after timeout) • Receiver expects new 0, …, 3, gets second incarnation of old 0, …, 3, incorrectly accepts as new In general, we need » S ≥ RWS + SWS 6
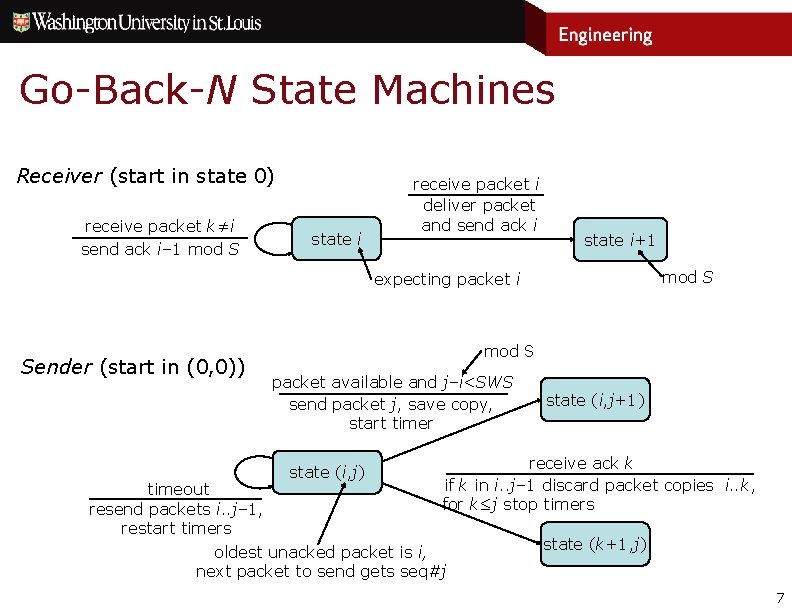
Go-Back-N State Machines Receiver (start in state 0) receive packet k≠i send ack i– 1 mod S state i receive packet i deliver packet and send ack i state i+1 mod S expecting packet i Sender (start in (0, 0)) timeout resend packets i. . j– 1, restart timers mod S packet available and j–i<SWS send packet j, save copy, start timer state (i, j) state (i, j+1) receive ack k if k in i. . j– 1 discard packet copies i. . k, for k≤j stop timers oldest unacked packet is i, next packet to send gets seq#j state (k+1, j) 7

Go-Back-N Performance n Performance depends on » Time-out value (timer starts when last bit of packet is sent) • Assume tout = ( - 1)tpkt ≥ RTT – As RTT increases, tout would increase • tpkt : transmission time of packet » Value of window size N • Assume N is large enough to keep the pipe full in the absence of losses, i. e. , (N– 1)tpkt > RTT » Impact and frequency of retransmissions n Expected Time for a Successful Packet Transmission: Tsucc » We need to know: • Time for the initial transmission: tpkt • Expected number of retransmissions: E[R] • Time for a single retransmission: Tr n Tsucc = E[R] Tr + tpkt 8

Go-Back-N Performance n Let Tr be the time spent for one retransmission » Tr = tpkt + tout = tpkt n Time spent per packet: T = RTr + tpkt » R is number of retransmissions (geometrically distributed) » E[R]=q/(1 -q), where q is the pkt loss probability n Expected time for successful packet transmission » Next pages show we get to the above equation n 100% throughput if tpkt = Tsucc » Achievable when q=0 (no pkt or ACK losses) » For a given value of q, throughput decreases as , i. e. , RTT, increases 9

Retransmissions as a Geometrically Distributed Random Variable n n Packet loss probability: q (we can ignore ack losses) R retransmissions means that packet transmissions fail R times before succeeding » P(R retransmissions) = q. R(1–q) n n E[R] = {R=0 to ∞}Rq. R(1–q) = q(1–q) {R=0 to ∞}Rq. R-1 = q(1–q)/(1–q)2 =q/(1–q) So a successful transmission requires one original transmission plus R retransmissions, for a total time of tpkt + R (tout + tpkt), or on average tpkt + tpkt x q/(1–q) = tpktx(1 + ( – 1)q)/(1–q) 10
![Go-Back-N Performance (continued) n Derivation of Tsucc » Tsucc = E[R] Ttotal + tpkt Go-Back-N Performance (continued) n Derivation of Tsucc » Tsucc = E[R] Ttotal + tpkt](http://slidetodoc.com/presentation_image_h/a74c95ee82c067cc509324221db7b980/image-11.jpg)
Go-Back-N Performance (continued) n Derivation of Tsucc » Tsucc = E[R] Ttotal + tpkt » E[R] = q/(1 -q) and Ttotal = tpkt » Tsucc = (q/(1 -q)) tpkt + tpkt (1 -q)/(1 -q) » Tsucc = (q tpkt /(1 -q)) + (tpkt - qtpkt )/(1 -q) » Tsucc = (q tpkt + tpkt - qtpkt )/(1 -q) » Tsucc = tpkt (q + 1 - q)/(1 -q) » Tsucc = (1 + ( - 1)q) tpkt /(1 -q) 11

Receive Buffer in Selective Repeat waiting for packet 1 7 0 1 2 6 5 n 4 3 Receiver maintains buffer of up to RWS=SWS=N packets » On receiving packet i, send ack i » If arriving packet is in window range and no previous copy is in buffer, store new packet » If arriving packet is next one expected • deliver it and all other packets up until the first “hole” in buffer • advance window to location of first hole n Correct operation calls for in-order packet delivery and S≥ 2 N (S is the number of sequence numbers) » Why? 12
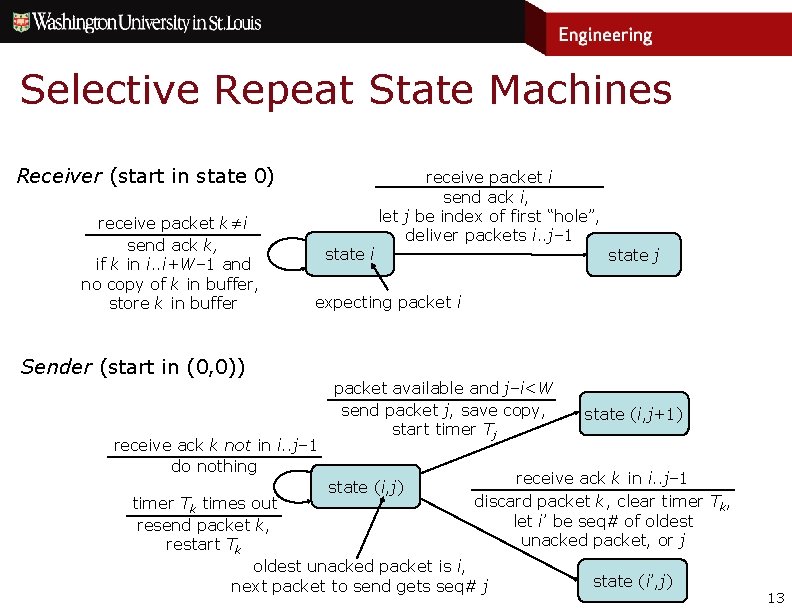
Selective Repeat State Machines Receiver (start in state 0) receive packet k≠i send ack k, if k in i. . i+W– 1 and no copy of k in buffer, store k in buffer state i receive packet i send ack i, let j be index of first “hole”, deliver packets i. . j– 1 state j expecting packet i Sender (start in (0, 0)) receive ack k not in i. . j– 1 do nothing packet available and j–i<W send packet j, save copy, start timer Tj state (i, j) state (i, j+1) receive ack k in i. . j– 1 discard packet k, clear timer Tk, let i’ be seq# of oldest unacked packet, or j timer Tk times out resend packet k, restart Tk oldest unacked packet is i, next packet to send gets seq# j state (i’, j) 13

Exercises 1. Draw a time-space diagram for the go-back-N protocol with N=3, S=6, assuming that five packets are sent, and the second and fifth packets are lost the first time they are sent. Show the states of the sender and receiver. 14
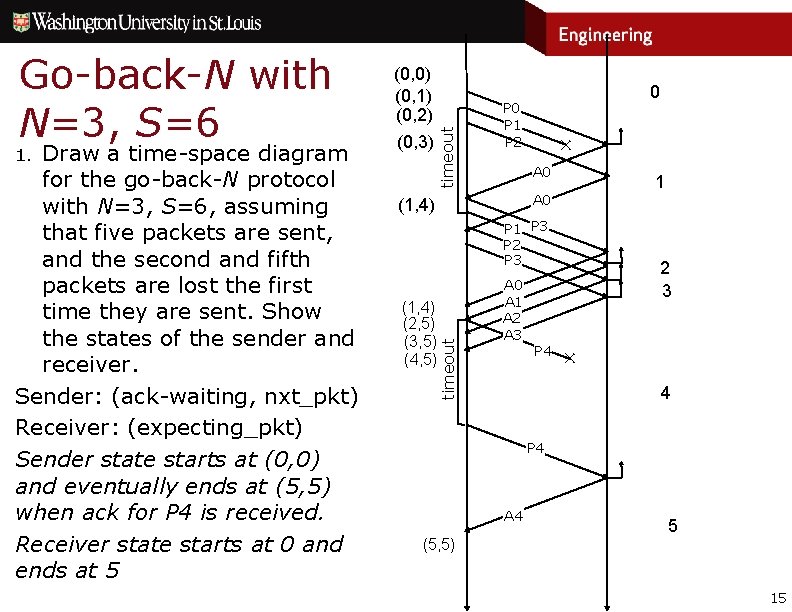
(0, 3) timeout Draw a time-space diagram for the go-back-N protocol with N=3, S=6, assuming that five packets are sent, and the second and fifth packets are lost the first time they are sent. Show the states of the sender and receiver. Sender: (ack-waiting, nxt_pkt) Receiver: (expecting_pkt) Sender state starts at (0, 0) and eventually ends at (5, 5) when ack for P 4 is received. Receiver state starts at 0 and ends at 5 1. (0, 0) (0, 1) (0, 2) 0 P 1 P 2 ✕ A 0 (1, 4) P 1 P 3 P 2 P 3 (1, 4) (2, 5) (3, 5) (4, 5) timeout Go-back-N with N=3, S=6 A 0 A 1 A 2 A 3 1 2 3 P 4 ✕ 4 P 4 A 4 5 (5, 5) 15

Exercises 2. Consider a link that uses go-back-N with S=10, N=5. Suppose 4 packets have been sent and 2 acks have been received. What is the smallest possible number of packets that could still be in the send buffer? What is the largest number? 16

Exercises 2. Consider a link that uses go-back-N with S=10, N=5. Suppose 4 packets have been sent and 2 acks have been received. What is the smallest possible number of packets that could still be in the send buffer? What is the largest number? Consider a scenario, where the first and second packets are lost. This will trigger ACKs when the third and fourth packets arrive, acknowledging receipt of the packet before the first (or the SYN packet). Under such a scenario, the two acks will not be for any of the four packets that have been sent, so that the sender will still have all four in its send buffer. In the best case, the two acks are for the 3 rd and 4 th packets and there are zero packets left in the send buffer (acks for packets 1 and 2 were lost). 17

Exercises 3. Draw a time-space diagram for the selective repeat protocol with N=3, S=6, assuming that five packets are sent, and the second and fifth packets are lost the first time they are sent. Show when each packet is delivered and the states of the sender and receiver at each step. 18
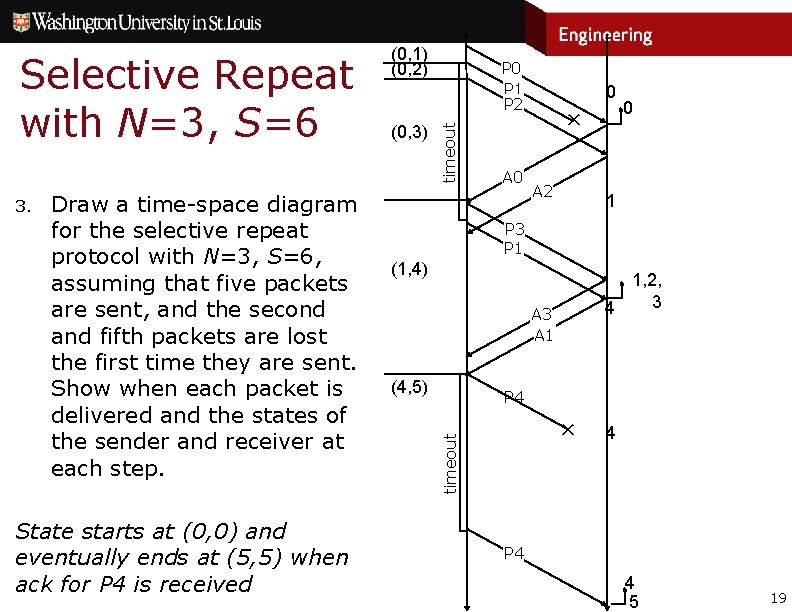
3. Draw a time-space diagram for the selective repeat protocol with N=3, S=6, assuming that five packets are sent, and the second and fifth packets are lost the first time they are sent. Show when each packet is delivered and the states of the sender and receiver at each step. State starts at (0, 0) and eventually ends at (5, 5) when ack for P 4 is received timeout (0, 3) P 0 P 1 P 2 A 0 0 ✕ A 2 0 1 P 3 P 1 (1, 4) 1, 2, 3 4 A 3 A 1 (4, 5) P 4 ✕ timeout Selective Repeat with N=3, S=6 (0, 1) (0, 2) 4 P 4 4 5 19

Exercises 4. Consider a link that uses selective repeat with S=10, N=5. Suppose 4 packets have been sent and 2 acks have been received. What is the smallest possible number of packets that could still be in the send buffer? What is the largest number? 20

Exercises 4. Consider a link that uses selective repeat with S=10, N=5. Suppose 4 packets have been sent and 2 acks have been received. What is the smallest possible number of packets that could still be in the send buffer? What is the largest number? With selective repeat, packets are acked individually. So in all cases, the receipt of two ACKs identifies two packets (out of four) that have been received. Hence, there will then be two packets in the sender’s send buffer (even if all four packets were successfully received). Note that in practice, selective acknowledgments are used in combination with cumulative ACKs, e. g. , through the use of a SACK option as in TCP (see RFC 2018). This helps overcome the fragility problem caused by requiring that each packet be individually acked. In particular, TCP’s SACK option allows the receiver to inform the sender of multiple (up to 4) non-contiguous blocks of data it received. It is used in combination with regular ACKs. 21
- Slides: 21