10 Firstorder Logic Limitation of propositional logic A








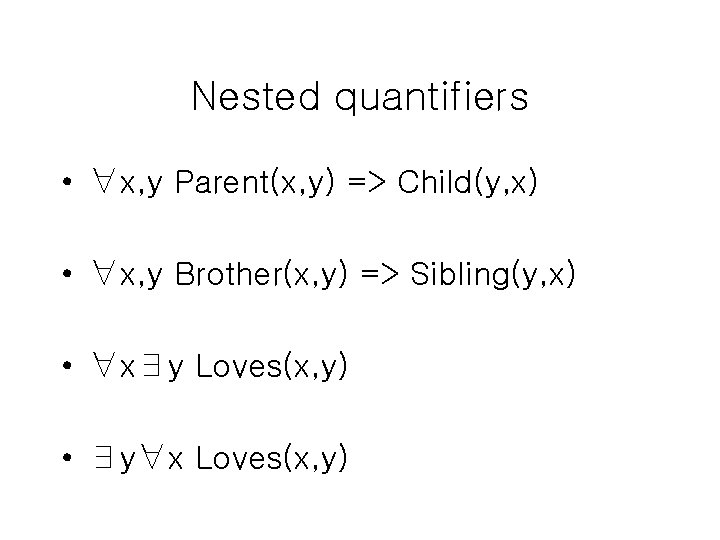


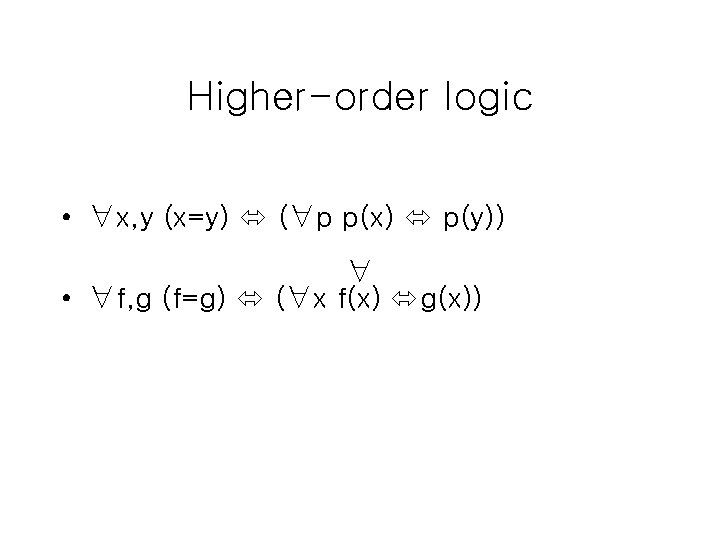








- Slides: 20

10주 강의 First-order Logic

Limitation of propositional logic • A very limited ontology • to need to the representation power • first-order logic

First-order logic • A stronger set of ontological commitments • A world in FOL consists of objects, properties, relations, functions • Objects people, houses, number, colors, Bill Clinton • Relations brother of, bigger than, owns, love • Properties red, round, bogus, prime • Functions father of, best friend, third inning of

Examples • “One plus two equals three” – objects : : one, two, three, one plus two – Relation : : equal – Function : : plus • “Squares neighboring the wumpus are smelly – Objects : : wumpus, square – Property : : smelly – Relation : : neighboring


Syntax and Semantics Sentence Atomic. Sentence | Sentence Connective Sentence | Auantifier Variable, …Sentence | (Sentence) Atomic. Sentence Predicate(Term, …) | Term=Term Function (Term, …) | Constant | Variable Connective | | | Quantifier | Constant A | X 1 | John | … Variable a | x | s | … Predicate Before | Han. Color | Raining | … Function Mother | Left. Leg. Of | … Figure 7. 1 The syntax of first-order logic (with equality) in BNF (Backus-Naur Form).

예 • • • Constant symbols : : A, B, John, Predicate symbols : : Round, Brother Function symbols : : Cosine, Father. Of Terms : : King John, Richard’s left leg Atomic sentences : : Brother(Richard, John), Married(Father. Of(Richard), Mother. Of(John)) • Complex sentences : : Older(John, 30)=>~younger(John, 30)

Quantifiers • World = {a, b, c} • Universal quantifier (∀) ∀x Cat(x) => Mammal(x) Cat(a) => Mammal(a) & Cat(a) => Mammal(a) • Existential quantifier (∃) ∃x Sister(x, Sopt) & Cat(x)
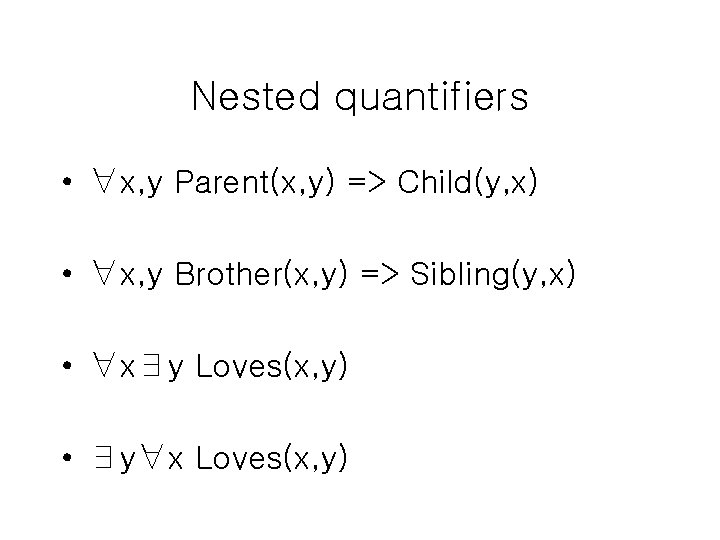
Nested quantifiers • ∀x, y Parent(x, y) => Child(y, x) • ∀x, y Brother(x, y) => Sibling(y, x) • ∀x∃y Loves(x, y) • ∃y∀x Loves(x, y)

De Morgan’s Rule ∀x ~P ~∃x P ~P&~Q ~(P v Q) ~∀x P ∃x ~P ~(P&Q) ~P v ~Q ∀x P ~∃x ~P P&Q ~(~P v ~ Q) ∃x P ~∀x ~P P v Q ~(~P&~Q)

Equality • Identity relation • Father(John) = Henry • ∃x, y Sister(Spot, x) & Sister(Spot, y) & ~(x=y) ≠ ∃x, y Sister(Spot, x) & Sister(Spot, y)
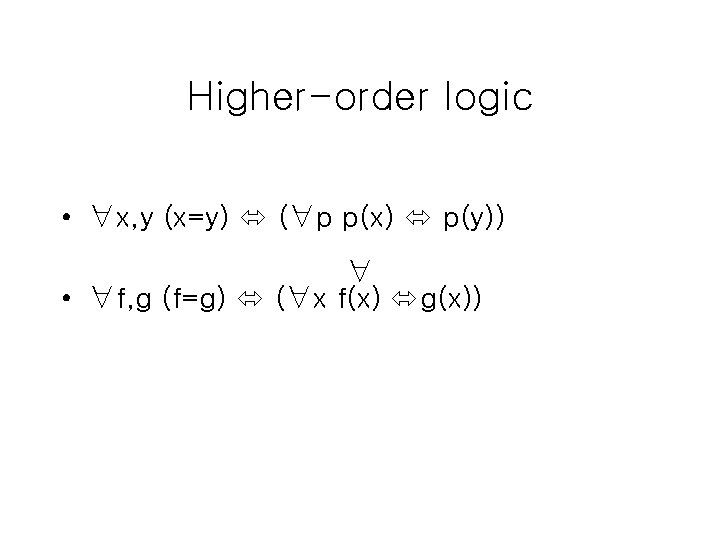
Higher-order logic • ∀x, y (x=y) (∀p p(x) p(y)) ∀ • ∀f, g (f=g) (∀x f(x) g(x))

-expression • x, y x 2 – y 2 • -expression can be applied to arguments to yield a logical term in the same way that a function can be • ( x, y x 2 – y 2)(25, 24) = 252 -242 = 49 • x, y Gender(x) ≠Gender(y) & Address(x) = Address(y)

∃! (The uniqueness quantifier) • ∃!x King(x) • ∃x King(x) & ∀y King(y) => x=y world를 고려하여 보여주면 => object가 1, 2, 3개일 때 {a} w 0 king={}, w 1 king={a} w 1만 model {a, b} w 0 king={}, w 1 king={a}, w 2 {b}, w 3 {a, b} w 1, w 2만 model

Representation of sentences by FOPL • One’s mother is one’s female parent ∀m, c Mother(c)=m Female(m) & Parent(m) • One’s husband is one’s male spouse ∀w, h Husband(h, w) Male(h) & Spouse(h, w) • Male and female are disjoint categories ∀x Male(x) ~Female(x) • A grandparent is a parent of one’s parent ∀g, c Grandparent(g, c) ∃p parent(g, p) & parent(p, g)

Representation of sentences by FOPL • A sibling is another child of one’s parents ∀x, y Sibling(x, y) x≠y & ∃p Parent(p, x) & Parent(p, y) • Symmetric relations ∀x, y Sibling(x, y) Sibling(y, x)

The domain of sets (I) • The only sets are the empty set and those made by adjoining something to a set : ∀s Set(s) (s=Empty. Set) v (∃x, s 2 Set(s 2) & s=Adjoin(x, s 2)) • The empty set has no elements adjoined into it. ~∃x, s Adjoin(x, s)=Empty. Set • Adjoining an element already in the set has no effect ∀x, s Member(x, s) s=Adjoin(x, s) • The only members of a set are the elements that were adjoined into it ∀x, s Member(x, s) ∃y, s 2 (s=Adjoin(y, s 2) & (x=y v Member(x, s)))

The domain of sets (II) • A set is a subset of another if and only if all of the first set’s are members of the second set : ∀s 1, s 2 Subset(s 1, s 2) (∀x Member(x, s 1) => member(x, s 2)) • Two sets are equal if and only if each is a subset of the other: ∀s 1, s 2 (s 1=s 2) (Subset(s 1, s 2) & Subset(s 2, s 1))

The domain of sets (III) • An object is a member of the intersection of two sets if and only if it is a member of each of sets : ∀x, s 1, s 2 Member(x, Intersection(s 1, s 2)) Member(x, s 1) & Member(x, s 2) • An object is a member of the union of two sets if and only if it is a member of either set : ∀x, s 1, s 2 Member(x, Union(s 1, s 2)) Member(x, s 1) v Member(x, s 2)

Asking questions and getting answers • Tell(KB, (∀m, c Mother(c)=m Female(m) & Parent(m, c))) • …… • Tell(KB, (Female(Maxi) & Parent(Maxi, Spot) & Parent(Spot, Boots))) • • Ask(KB, Grandparent(Maxi, Boots) Ask(KB, ∃x Child(x, Spot)) Ask(KB, ∃x Mother(x)=Maxi) Substitution, unification, {x/Boots}