10 Chapter 10 Metric Path Planning 10 Objectives

10 Chapter 10: Metric Path Planning

10 Objectives • Define Cspace, path relaxation, digitization bias, subgoal obsession, termination condition • Explain the difference between graph and wavefront planners • Represent an indoor environment with a GVG, a regular grid, or a quadtree, and create a graph suitable for path planning • Apply A* search • Apply wavefront propagation • Explain the differences between continuous and event-driven replanning Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 2
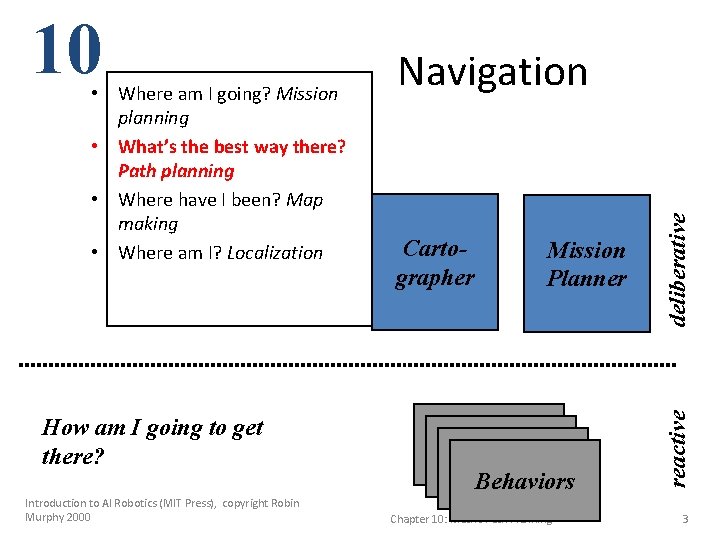
How am I going to get there? Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Cartographer Mission Planner Behaviors Chapter 10: Metric Path Planning deliberative • Where am I going? Mission planning • What’s the best way there? Path planning • Where have I been? Map making • Where am I? Localization Navigation reactive 10 3

10 Overview • Metric Path Planning vs Topological Methods – Metric methods generally favor techniques which produce an optimal according to some measure of best. – While the later produce a route with identifiable landmarks – Metrics Decompose the path into sub-goals consisting of way-points. E. g. coordinates(x, y) – Topological focuses on subgoals which are gateways – Metric methods are compatible with deliberation while Topological are compatible with reactive Ø Metric Path Planners have two components 1. Representation : salient features, relevant configuration space Popular: Regular grids, 2. Algorithm: two types a. those which treat path planning as a graph search problem b. “ “ “ graphics coloring problem. Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 4
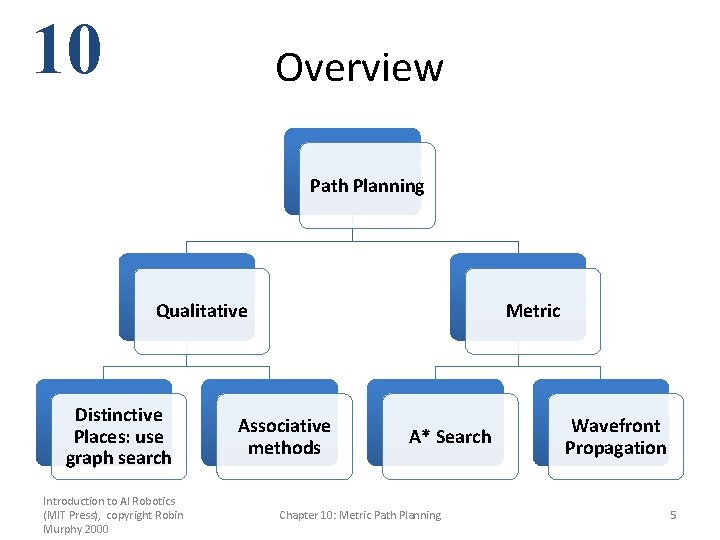
10 Overview Path Planning Qualitative Distinctive Places: use graph search Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Metric Associative methods A* Search Chapter 10: Metric Path Planning Wavefront Propagation 5

10 Spatial Memory • What’s the Best Way There? depends on the representation of the world • A robot’s world representation and how it is maintained over time is its spatial memory – – Attention Reasoning Path planning Information collection • Two forms – Route (or qualitative) – Layout (or metric) • Layout leads to Route, but not the other way Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 6

10 Representing Area/Volume in Path Planning • In Quantitative or metric maps: – Rep: Many different ways to represent an area or volume of space • Looks like a “bird’s eye” view, position & viewpoint independent – Algorithms • Graph or network algorithms • Wavefront or graphics-derived algorithms Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 7

10 Metric Maps • Motivation for having a metric map is often path planning (others include reasoning about space…) • Determine a path from one point to goal – Generally interested in “best” or “optimal” – What are measures of best/optimal? – Relevant: occupied or empty • Path planning assumes an a priori map of relevant aspects – Only as good as last time map was updated Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 8
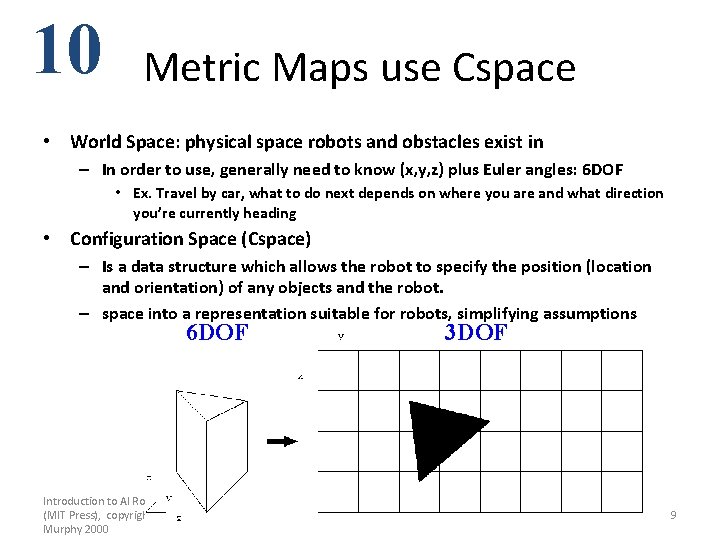
10 Metric Maps use Cspace • World Space: physical space robots and obstacles exist in – In order to use, generally need to know (x, y, z) plus Euler angles: 6 DOF • Ex. Travel by car, what to do next depends on where you are and what direction you’re currently heading • Configuration Space (Cspace) – Is a data structure which allows the robot to specify the position (location and orientation) of any objects and the robot. – space into a representation suitable for robots, simplifying assumptions 6 DOF Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 3 DOF Chapter 10: Metric Path Planning 9

10 Major Cspace Representations • Idea: reduce physical space to a cspace representation which is more amenable for storage in computers and for rapid execution of algorithms • Major types – Meadow Maps – Generalized Voronoi Graphs (GVG) – Regular grids, quadtrees Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 10
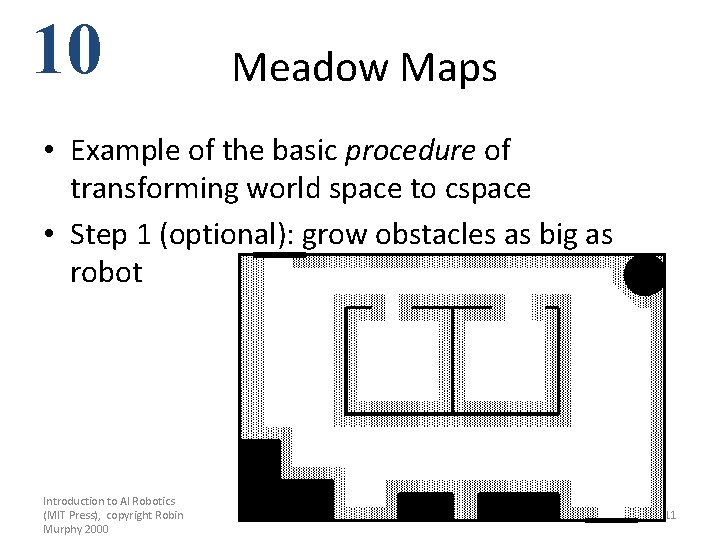
10 Meadow Maps • Example of the basic procedure of transforming world space to cspace • Step 1 (optional): grow obstacles as big as robot Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 11
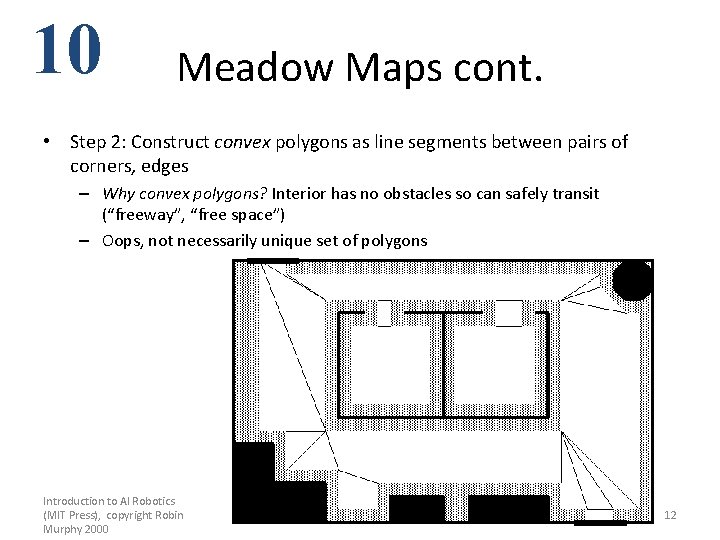
10 Meadow Maps cont. • Step 2: Construct convex polygons as line segments between pairs of corners, edges – Why convex polygons? Interior has no obstacles so can safely transit (“freeway”, “free space”) – Oops, not necessarily unique set of polygons Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 12
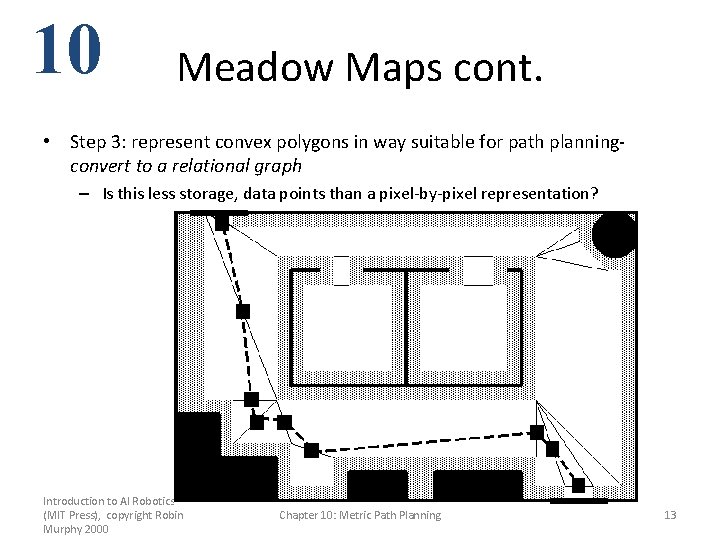
10 Meadow Maps cont. • Step 3: represent convex polygons in way suitable for path planningconvert to a relational graph – Is this less storage, data points than a pixel-by-pixel representation? Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 13

10 Problems with Meadow Maps • Not unique generation of polygons • Could you actually create this type of map with sensor data? • How does it tie into actually navigating the path? – How does robot recognize “right” corners, edges and go to “middle”? – What about sensor noise? Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 14
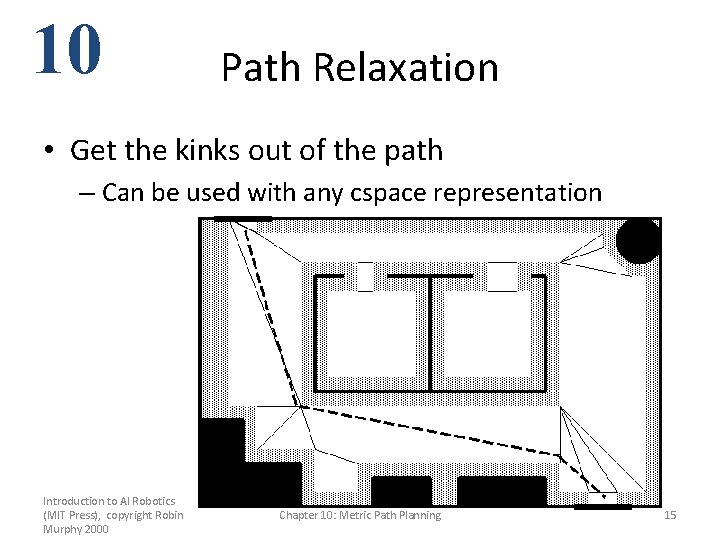
10 Path Relaxation • Get the kinks out of the path – Can be used with any cspace representation Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 15
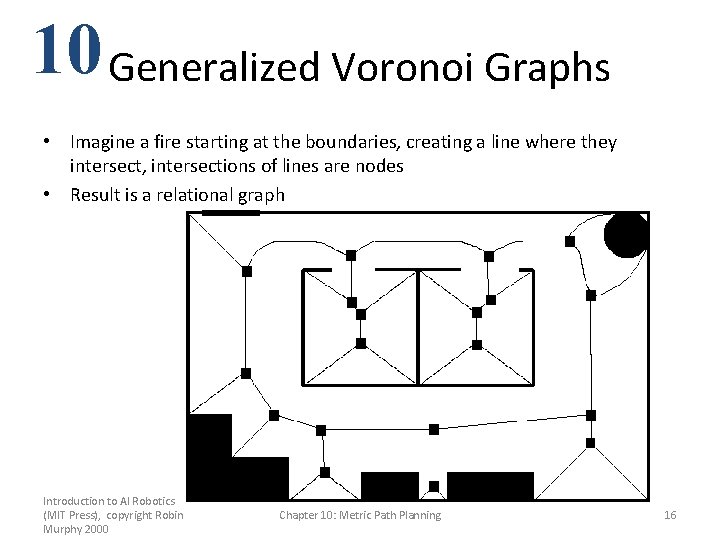
10 Generalized Voronoi Graphs • Imagine a fire starting at the boundaries, creating a line where they intersect, intersections of lines are nodes • Result is a relational graph Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 16

10 Regular Grids • Bigger than pixels, but same idea – Often on order of 4 inches square – Make a relational graph by each element as a node, connecting neighbors (4 connected, 8 -connected) – Moore’s law effect: fast processors, cheap hard drives, who cares about overhead anymore? Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 17

10 Problems with GVG and Regular Grids • GVG – Sensitive to sensor noise – Path execution: requires robot to be able to sense boundaries • Grids – World doesn’t always line up on grids – Digitalization bias: left over space marked as occupied Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 18

10 Summary of Representations • Metric path planning requires – Representation of world space, usually try to simplify to cspace – Algorithms which can operate over representation to produce best/optimal path • Representation – Usually try to end up with relational graph – Regular grids are currently most popular in practice, GVGs are interesting – Tricks of the trade • Grow obstacles to size of robot to be able to treat holonomic robots as point • Relaxation (string tightening) • Metric methods often ignore issue of – how to execute a planned path – Impact of sensor noise or uncertainty, localization Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 19

10 Algorithms • For Path planning – A* for relational graphs – Wavefront for operating directly on regular grids • For Interleaving Path Planning and Execution Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 20

10 Motivation for A* • Single Source Shortest Path algorithms are exhaustive, visiting all edges – Can’t we throw away paths when we see that they aren’t going to the goal, rather than follow all branches? • This means having a mechanism to “prune” branches as we go, rather than after full exploration • Algorithms which prune earlier (but correctly) are preferred over algorithms which do it later. Issue -> the mechanism for pruning Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 21

10 A* • Similar to breadth-first: at each point in the time the planner can only “see” it’s node and 1 set of nodes “in front” • Idea is to rate the choices, choose the best one first, throw away any choices whenever you can f*(n)=g*(n)+h*(n) • f*(n) is the “goodness” of the path from Start to n • g*(n) is the “cost” of going from the Start to node n • H*(n) is the cost of going from n to the Goal – H is for “heuristic function” because must have a way of guessing the cost of n to Goal since can’t see the path between n and the Goal Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 22

10 A* Heuristic Function f*(n)=g*(n)+h*(n) • G*(n) is easy: just sum up the path costs to n • H*(n) is tricky – But path planning requires an a priori map – Metric path planning requires a METRIC a priori map – Therefore, know the distance between Initial and Goal nodes, just not the optimal way to get there – H*(n)= distance between n and Goal Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 23
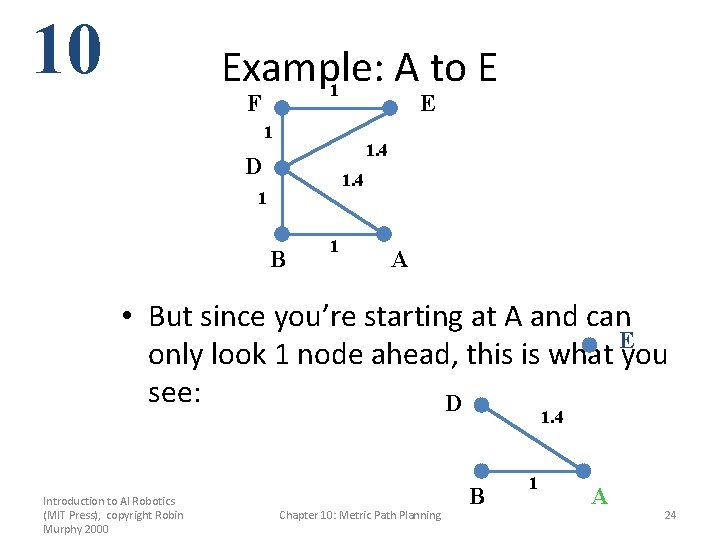
10 Example: A to E 1 F E 1 1. 4 D 1. 4 1 B 1 A • But since you’re starting at A and can E only look 1 node ahead, this is what you see: D 1. 4 Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning B 1 A 24
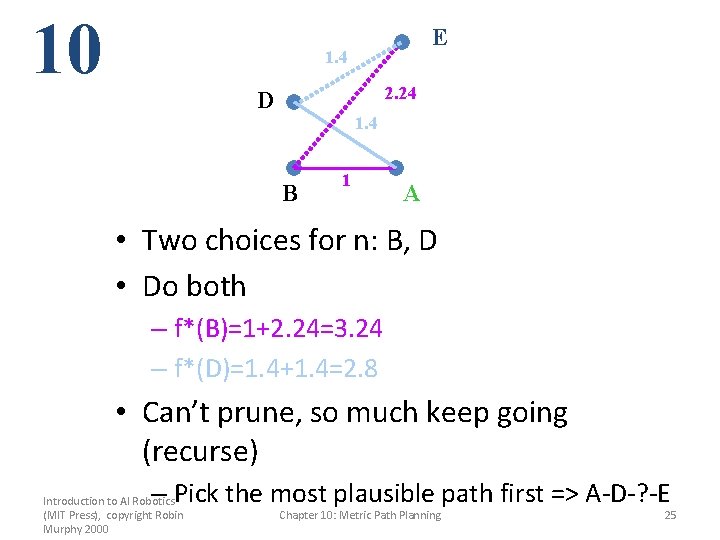
10 E 1. 4 2. 24 D 1. 4 B 1 A • Two choices for n: B, D • Do both – f*(B)=1+2. 24=3. 24 – f*(D)=1. 4+1. 4=2. 8 • Can’t prune, so much keep going (recurse) – Pick the most plausible path first => A-D-? -E Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 25
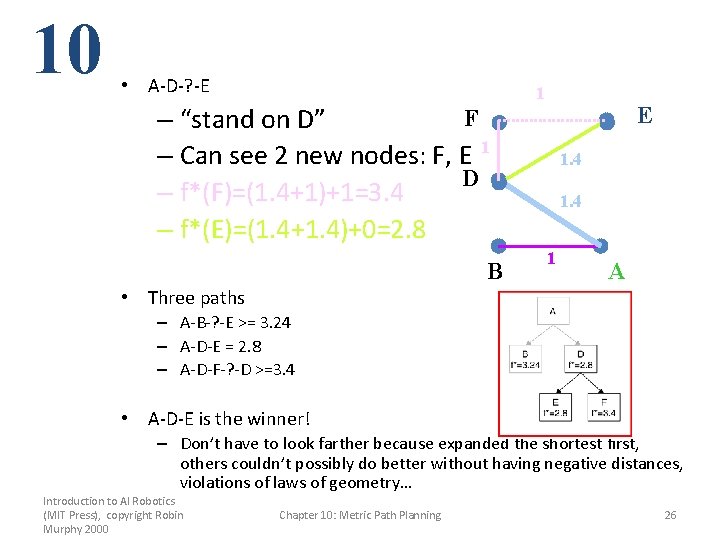
10 • A-D-? -E F – “stand on D” – Can see 2 new nodes: F, E 1 D – f*(F)=(1. 4+1)+1=3. 4 – f*(E)=(1. 4+1. 4)+0=2. 8 B 1 E 1. 4 1 A • Three paths – A-B-? -E >= 3. 24 – A-D-E = 2. 8 – A-D-F-? -D >=3. 4 • A-D-E is the winner! – Don’t have to look farther because expanded the shortest first, others couldn’t possibly do better without having negative distances, violations of laws of geometry… Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 26

10 Wavefront Planners Idea: • Considers the Cspace to be a conductive material with heat radiating out from the initial node to the goal node. • Obstacles have conductivity 0. 0 • Open area infinite conductivity but undesirable terrains, which are traversable are given lower conductivity • Consider Region coloring in graphics, where color spreads out to neighboring pixels Result: • A map which looks like a potential field Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 27
10 Wavefront Planners Well suited for grid types of representations Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 28

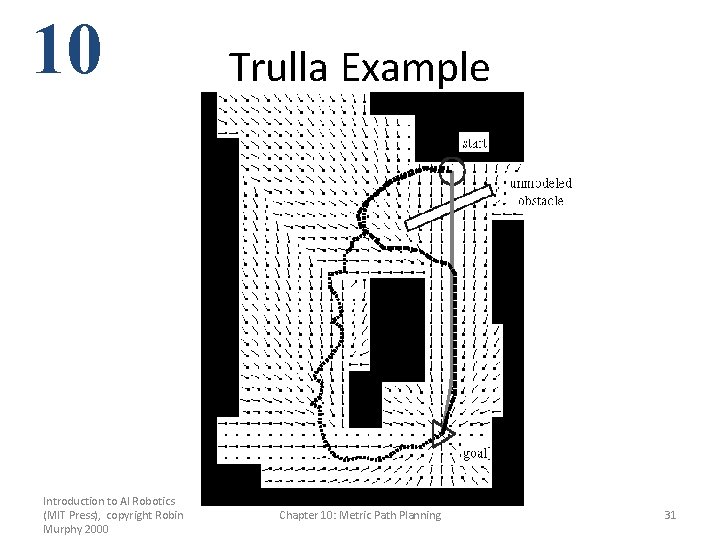
10 Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Trulla Chapter 10: Metric Path Planning 29

10 Interleaving Path Planning and Reactive Execution • Most Path Planning algorithms are employed in strictly plan once, then reactively execute styles. • Graph-based planners generate a path and subpaths or subsegments • Recall NHC, Au. RA – Pilot looks at current subpath, instantiates behaviors to get from current location to subgoal • What happens if blocked? What happens if avoid an obstacle and actually is now closer to the next subgoal? – Causes Subgoal obsession • When does the robot think it has reached (x, y)? What about encoder error? – Need a Termination condition, usually +/- width of robot Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 30
10 Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Trulla Example Chapter 10: Metric Path Planning 31

10 Two Example Approaches • If compute all possible paths in advance, not a problem – Shortest path between pairs will be part of shortest path to more distant pairs • D* – Tony Stentz – Run A* over all possible pairs of nodes – Dynamically repair A* paths affected by the changes in the map • Trulla – Ken Hughes – By-product of wave propagation style is path to everywhere Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 32

10 Summary • Metric path planners – graph-based (A* is best known) – Wavefront • Graph-based generate paths and subgoals. – Good for NHC styles of control – In practice leads to: • Subgoal obsession • Termination conditions • Planning all possible paths helps with subgoal obsession – What happens when the map is wrong, things change, missed opportunities? How can you tell when the map is wrong or that’s it worth the computation? Introduction to AI Robotics (MIT Press), copyright Robin Murphy 2000 Chapter 10: Metric Path Planning 33
- Slides: 33