10 7 Stationary waves in an open pipe



- Slides: 9

10. 7 Stationary waves in an open pipe © Manhattan Press (H. K. ) Ltd. 1

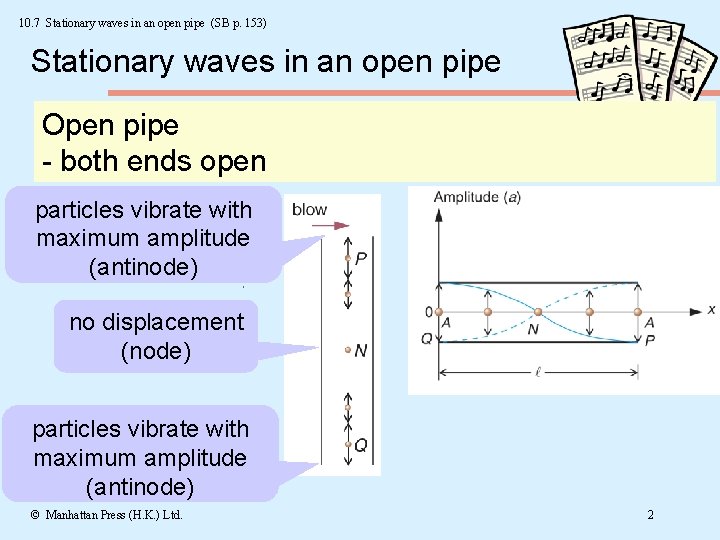
10. 7 Stationary waves in an open pipe (SB p. 153) Stationary waves in an open pipe Open pipe - both ends open particles vibrate with maximum amplitude (antinode) no displacement (node) particles vibrate with maximum amplitude (antinode) © Manhattan Press (H. K. ) Ltd. 2

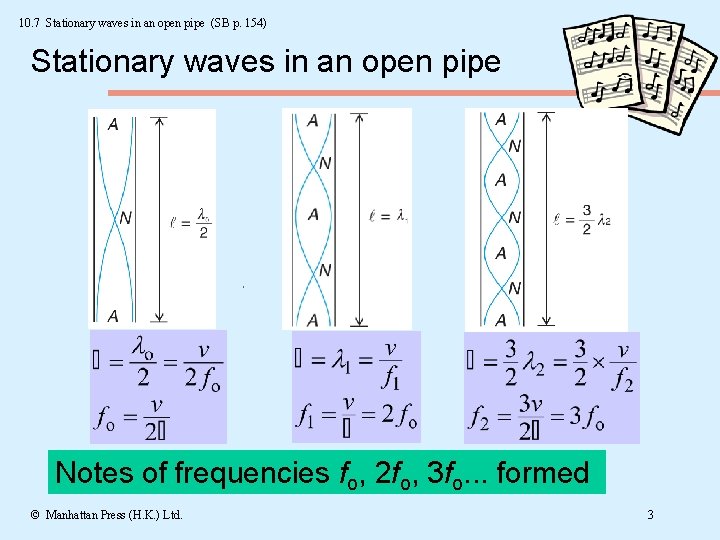
10. 7 Stationary waves in an open pipe (SB p. 154) Stationary waves in an open pipe Notes of frequencies fo, 2 fo, 3 fo. . . formed © Manhattan Press (H. K. ) Ltd. 3

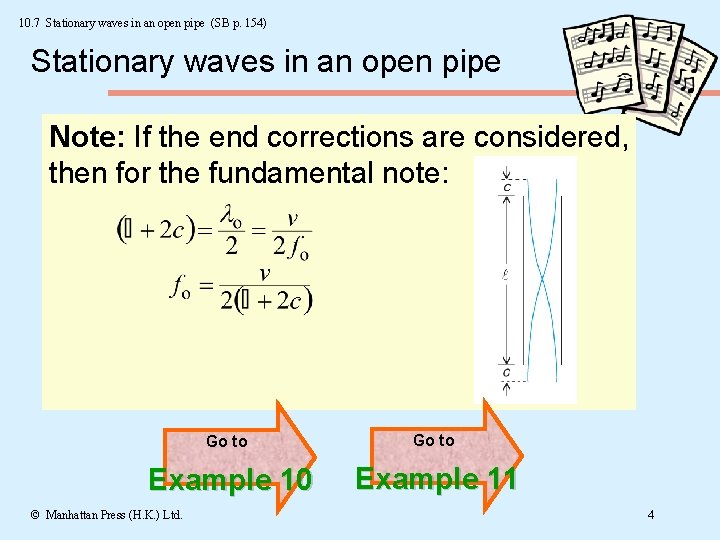
10. 7 Stationary waves in an open pipe (SB p. 154) Stationary waves in an open pipe Note: If the end corrections are considered, then for the fundamental note: Go to Example 10 Example 11 © Manhattan Press (H. K. ) Ltd. 4

End © Manhattan Press (H. K. ) Ltd. 5

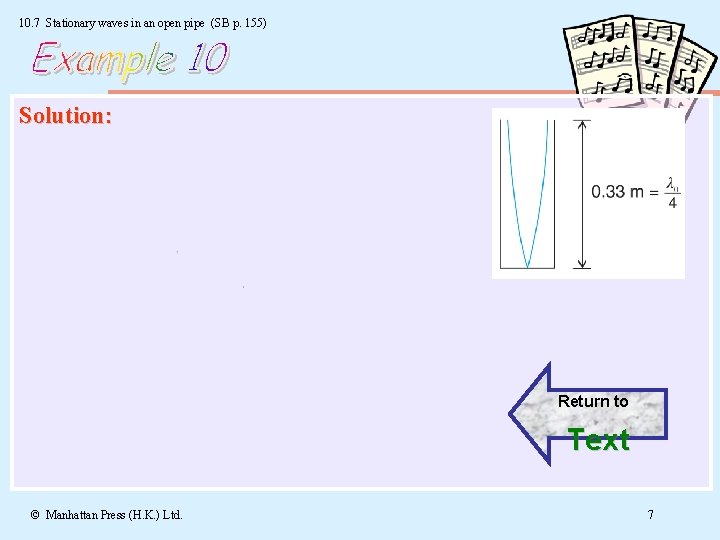
10. 7 Stationary waves in an open pipe (SB p. 155) Q: An organ pipe is 0. 33 m long, open at one end and closed at the other. Assuming that end corrections are negligible and the speed of sound is 330 m s– 1, calculate (a) the frequencies of the fundamental and the first overtone, and (b) the length of a pipe which is open at both ends and has a fundamental frequency equal to the difference of the frequencies calculated in (a). Solution © Manhattan Press (H. K. ) Ltd. 6

10. 7 Stationary waves in an open pipe (SB p. 155) Solution: Return to Text © Manhattan Press (H. K. ) Ltd. 7

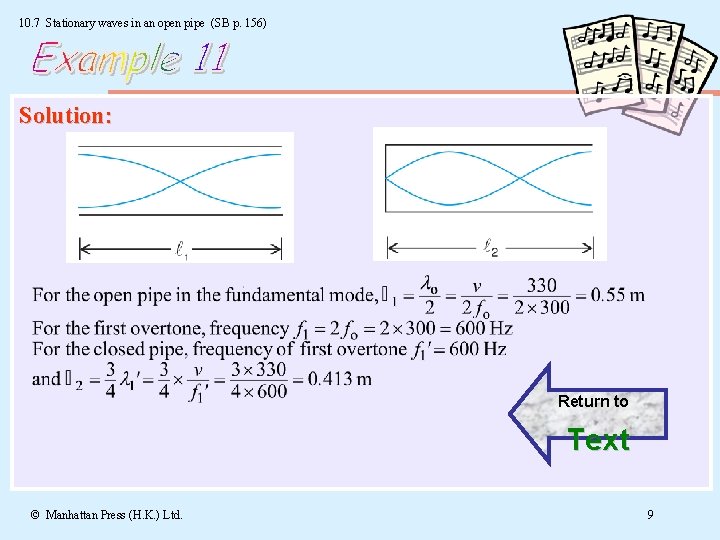
10. 7 Stationary waves in an open pipe (SB p. 156) Q: An open pipe has a fundamental frequency of 300 Hz. The first overtone of a closed pipe has the same frequency as the first overtone of the open pipe. What is the length of each pipe? Assume that end corrections are negligible and the speed of sound in air is 330 m s– 1. Solution © Manhattan Press (H. K. ) Ltd. 8

10. 7 Stationary waves in an open pipe (SB p. 156) Solution: Return to Text © Manhattan Press (H. K. ) Ltd. 9