10 5 Hyperbolas Hyperbola Hyperbolas Has two smooth

10 – 5 Hyperbolas

Hyperbola

Hyperbolas • Has two smooth branches • The turning point of each branch is the vertex • Transverse Axis: segment connecting the two vertices • The two foci lie on the axis of symmetry • The center of the hyperbola is the midpoint between the two vertices or the foci • The Conjugate Axis and the Transverse Axis determine a rectangle that lies between the vertices, and the diagonals of the rectangle determine the asymptotes

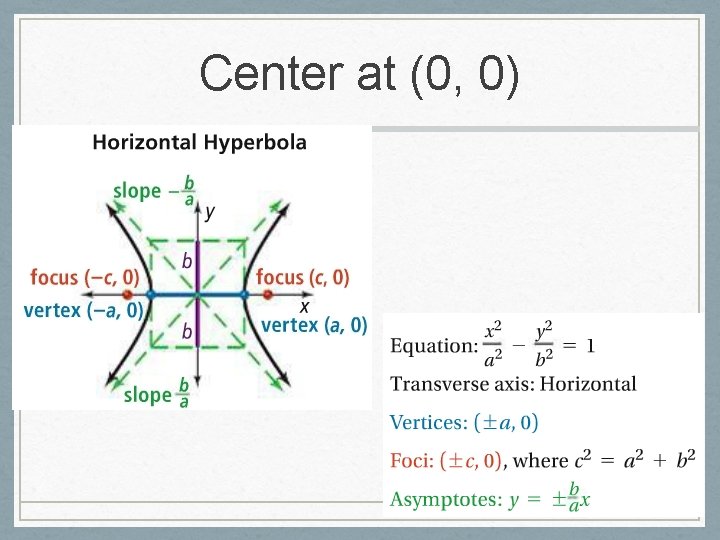
Center at (0, 0)

Vertical; Center (0, 0)

Writing and Graphing • A hyperbola centered at (0, 0) has vertices (± 4, 0) and one focus (5, 0) • What is the standard form equation? • Sketch the Hyperbola • A hyperbola centered at (0, 0) has vertices (0, ± 4) and one focus (0, 5) • What is the standard form equation? • Sketch the Hyperbola

Analyzing • What are the vertices, foci, and asymptotes of the hyperbola • 9 y 2 – 7 x 2 = 63 • 9 x 2 – 4 y 2 = 36

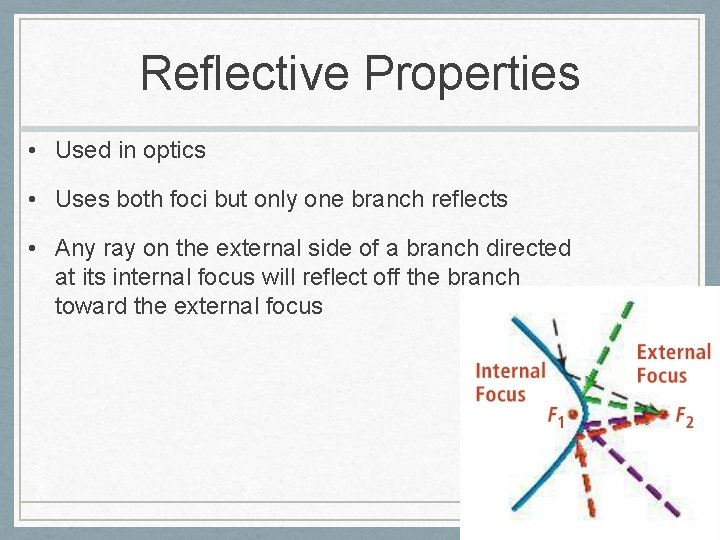
Reflective Properties • Used in optics • Uses both foci but only one branch reflects • Any ray on the external side of a branch directed at its internal focus will reflect off the branch toward the external focus

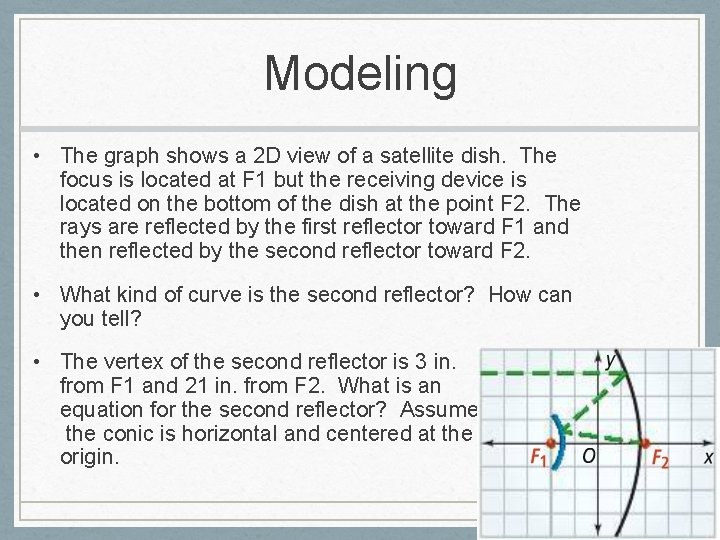
Modeling • The graph shows a 2 D view of a satellite dish. The focus is located at F 1 but the receiving device is located on the bottom of the dish at the point F 2. The rays are reflected by the first reflector toward F 1 and then reflected by the second reflector toward F 2. • What kind of curve is the second reflector? How can you tell? • The vertex of the second reflector is 3 in. from F 1 and 21 in. from F 2. What is an equation for the second reflector? Assume the conic is horizontal and centered at the origin.

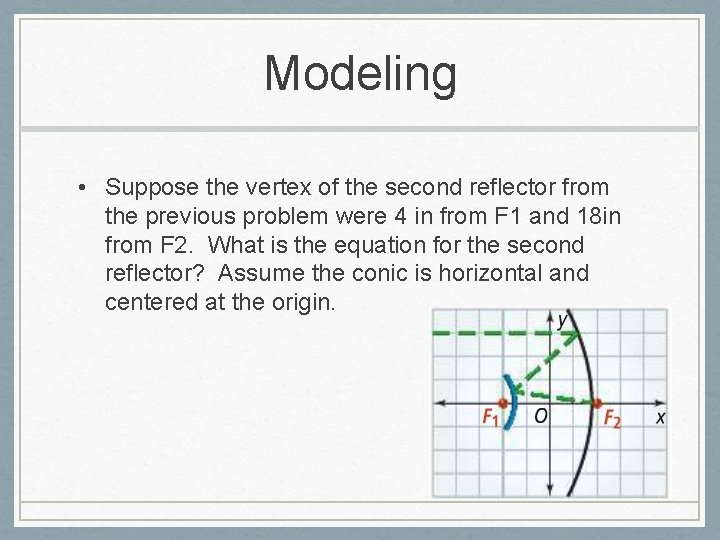
Modeling • Suppose the vertex of the second reflector from the previous problem were 4 in from F 1 and 18 in from F 2. What is the equation for the second reflector? Assume the conic is horizontal and centered at the origin.

Homework • Pg. 650 • # 8 – 30 even, 42 • 13 problems