10 4 The Pendulum Period of a Simple





- Slides: 8

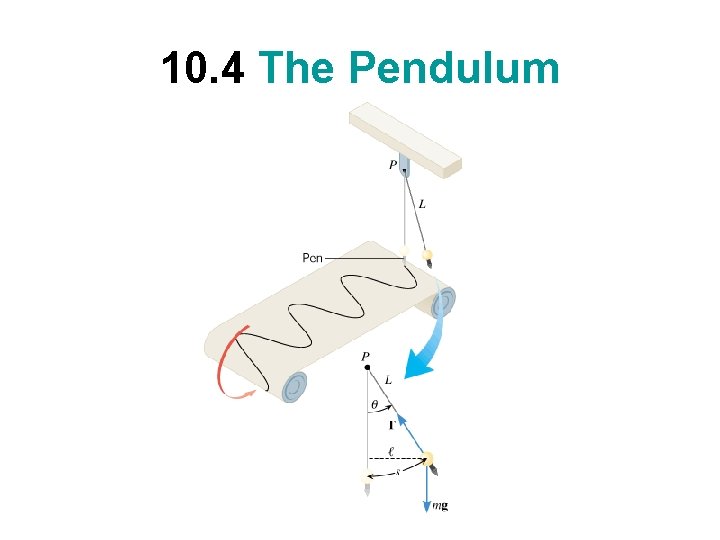
10. 4 The Pendulum

Period of a Simple Pendulum

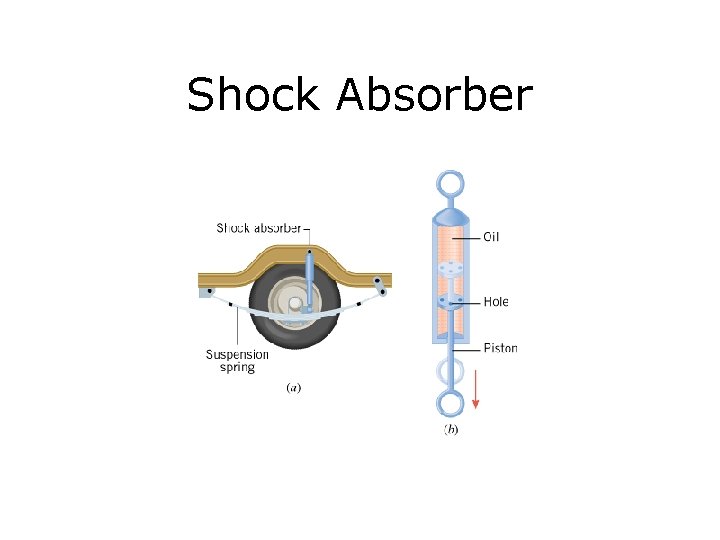
10. 5. Damped Harmonic Motion In simple harmonic motion, an object oscillates with a constant amplitude. In the presence of energy dissipation, the amplitude of oscillation decreases as time passes, and the motion is referred to as damped harmonic motion.

Shock Absorber

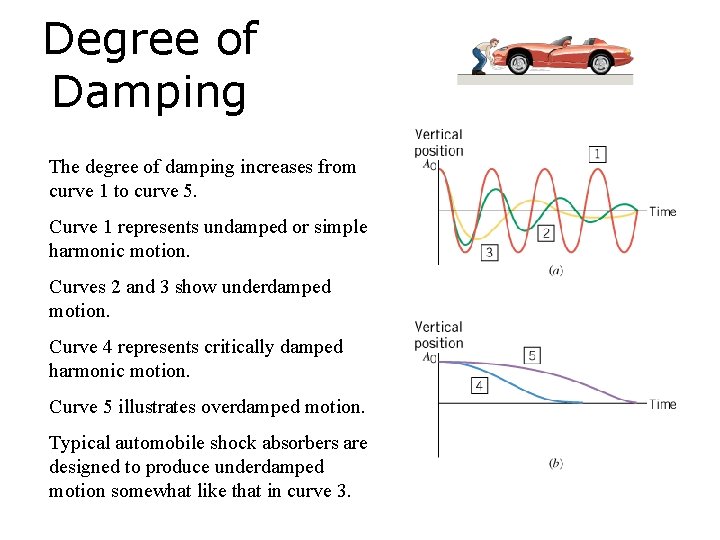
Degree of Damping The degree of damping increases from curve 1 to curve 5. Curve 1 represents undamped or simple harmonic motion. Curves 2 and 3 show underdamped motion. Curve 4 represents critically damped harmonic motion. Curve 5 illustrates overdamped motion. Typical automobile shock absorbers are designed to produce underdamped motion somewhat like that in curve 3.

10. 6 Driven Harmonic Motion and Resonance To set an object on an ideal spring into simple harmonic motion, some agent must apply a force that stretches or compresses the spring initially. Suppose that this force is applied at all times, not just for a brief initial moment. The resulting motion is known as driven harmonic motion, because the additional force drives or controls the behavior of the object to a large extent. The additional force is identified as the driving force.

Resonance occurs when the frequency of the driving force (blue arrows) matches a frequency at which the object naturally vibrates. The red arrows represent the velocity of the object.

Greatest Tides in the World Figure 10. 27 The Bay of Fundy at (a) high tide and (b) low tide. In some places the water level changes by almost 15 m. This phenomenon is partly due to resonance. The time, or period, that it takes for the tide to flow into and ebb out of a bay depends on the size of the bay, the topology of the bottom, and the configuration of the shoreline. The ebb and flow of the water in the Bay of Fundy has a period of 12. 5 hours, which is very close to the lunar tidal period of 12. 42 hours. The tide then “drives” water into and out of the Bay of Fundy at a frequency (once per 12. 42 hours) that nearly matches the natural frequency of the bay (once per 12. 5 hours). The result is the extraordinary high tide in the bay.