10 4 Pascals Triangle and the Binomial Theorem

10. 4 – Pascal’s Triangle and the Binomial Theorem

FACTORIALS, COMBINATIONS Factorial is denoted by the symbol “!”. The factorial of a number is calculated by multiplying all integers from the number to 1. Formal Definition The symbol n!, is define as the product of all the integers from n to 1. In other words, n! = n(n - 1)(n – 2)(n – 3) · · · 3 · 2 · 1 Also note that by definition, 0! = 1 Example #9

Combinations Definition Combinations give the number of ways x element can be selected from n distinct elements. The total number of combinations is given by, and is read as “the number of combinations of n elements selected x at a time. ” The formula for the number of combinations for selecting x from n distinct elements is, Note:

Combinations Example #10

The Binomial Theorem Strategy only: how do we expand these? 1. 3. (x + 2)2 (x – 3)3 2. 4. (2 x + 3)2 (a + b)4

The Binomial Theorem Solutions 1. (x + 2)2 = x 2 + 2(2)x + 22 = x 2 + 4 x + 4 2. (2 x + 3)2 = (2 x)2 + 2(3)(2 x) + 32 = 4 x 2 + 12 x + 9 3. (x – 3)3 = (x – 3)2 = (x – 3)(x 2 – 2(3)x + 32) = (x – 3)(x 2 – 6 x + 9) = x(x 2 – 6 x + 9) – 3(x 2 – 6 x + 9) = x 3 – 6 x 2 + 9 x – 3 x 2 + 18 x – 27 = x 3 – 9 x 2 + 27 x – 27 4. (a + b)4 = (a + b)2 = (a 2 + 2 ab + b 2) = a 2(a 2 + 2 ab + b 2) + 2 ab(a 2 + 2 ab + b 2) + b 2(a 2 + 2 ab + b 2) = a 4 + 2 a 3 b + a 2 b 2 + 2 a 3 b + 4 a 2 b 2 + 2 ab 3 + b 4 = a 4 + 4 a 3 b + 6 a 2 b 2 + 4 ab 3 + b 4 5. (a + b)5

THAT is a LOT of work! Isn’t there an easier way?

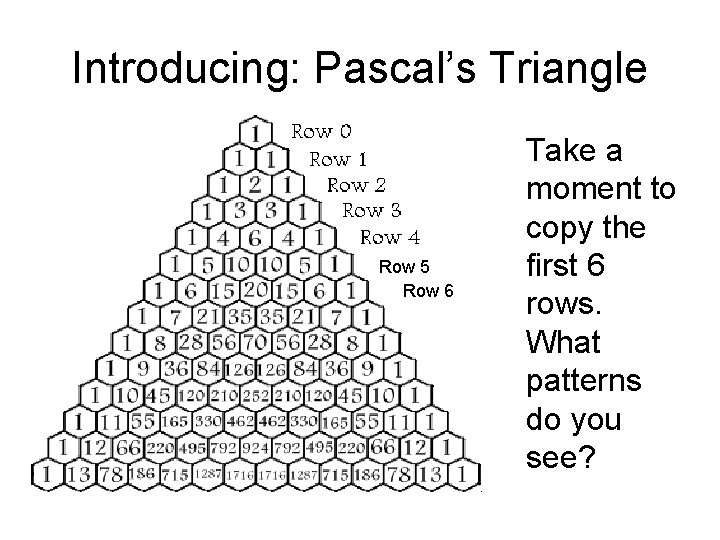
Introducing: Pascal’s Triangle Row 5 Row 6 Take a moment to copy the first 6 rows. What patterns do you see?

The Binomial Theorem Use Pascal’s Triangle to expand (a + b)5. Use the row that has 5 as its second number. The exponents for a begin with 5 and decrease. 1 a 5 b 0 + 5 a 4 b 1 + 10 a 3 b 2 + 10 a 2 b 3 + 5 a 1 b 4 + 1 a 0 b 5 The exponents for b begin with 0 and increase. In its simplest form, the expansion is a 5 + 5 a 4 b + 10 a 3 b 2 + 10 a 2 b 3 + 5 ab 4 + b 5. Row 5

The Binomial Theorem Use Pascal’s Triangle to expand (x – 3)4. First write the pattern for raising a binomial to the fourth power. 1 4 6 4 1 Coefficients from Pascal’s Triangle. (a + b)4 = a 4 + 4 a 3 b + 6 a 2 b 2 + 4 ab 3 + b 4 Since (x – 3)4 = (x + (– 3))4, substitute x for a and – 3 for b. (x + (– 3))4 = x 4 + 4 x 3(– 3) + 6 x 2(– 3)2 + 4 x(– 3)3 + (– 3)4 = x 4 – 12 x 3 + 54 x 2 – 108 x + 81 The expansion of (x – 3)4 is x 4 – 12 x 3 + 54 x 2 – 108 x + 81.

The Binomial Theorem For any positive integer, n

The Binomial Theorem Use the Binomial Theorem to expand (x – y)9. Write the pattern for raising a binomial to the ninth power. (a + b)9 = 9 C 0 a 9 + 9 C 1 a 8 b + 9 C 2 a 7 b 2 + 9 C 3 a 6 b 3 + 9 C 4 a 5 b 4 + 9 C 5 a 4 b 5 + 9 C 6 a 3 b 6 + 9 C 7 a 2 b 7 + 9 C 8 ab 8 + 9 C 9 b 9 Substitute x for a and –y for b. Evaluate each combination. (x – y)9 = 9 C 0 x 9 + 9 C 1 x 8(–y) + 9 C 2 x 7(–y)2 + 9 C 3 x 6(–y)3 + 9 C 4 x 5(–y)4 + 9 C 5 x 4(–y)5 + 9 C 6 x 3(–y)6 + 9 C 7 x 2(–y)7 + 9 C 8 x(–y)8 + 9 C 9(–y)9 = x 9 – 9 x 8 y + 36 x 7 y 2 – 84 x 6 y 3 + 126 x 5 y 4 – 126 x 4 y 5 + 84 x 3 y 6 – 36 x 2 y 7 + 9 xy 8 – y 9 The expansion of (x – y)9 is x 9 – 9 x 8 y + 36 x 7 y 2 – 84 x 6 y 3 + 126 x 5 y 4 – 126 x 4 y 5 + 84 x 3 y 6 – 36 x 2 y 7 + 9 xy 8 – y 9.

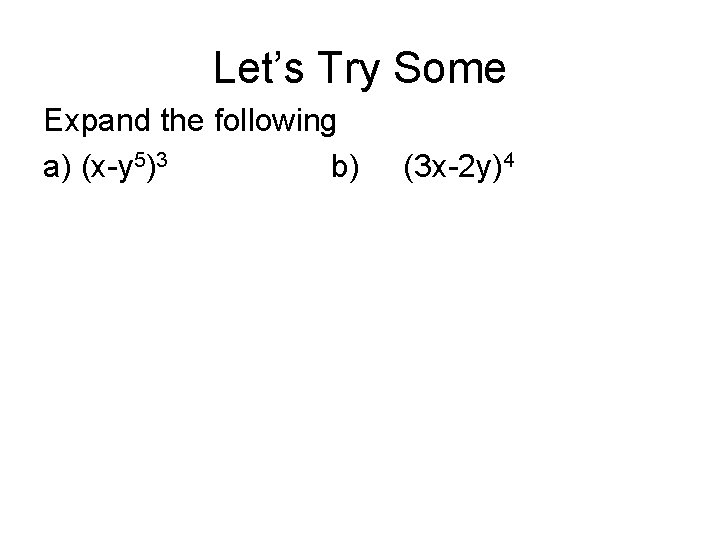
Let’s Try Some Expand the following a) (x-y 5)3 b) (3 x-2 y)4

Let’s Try Some Expand the following (x-y 5)3

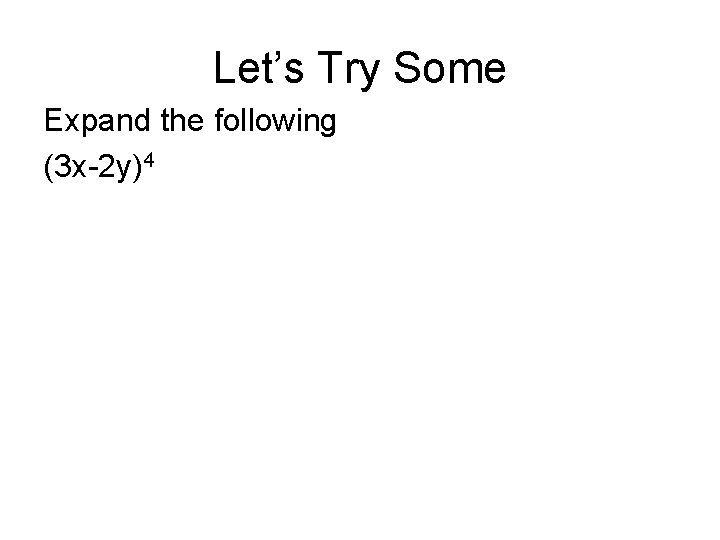
Let’s Try Some Expand the following (3 x-2 y)4

Let’s Try Some Expand the following (3 x-2 y)4