10 3 The gas law v Four variables

10. 3 The gas law v Four variables are needed to define the physical condition or state of a gas, temperature, T, pressure, P, volume, V and amount of gas (in mole), n. v The equations that express the relationships among T, P, V and n are known as the gas laws. The pressure-volume relationship: Boyle's law Boyle’s law states that the volume (V) of a fixed quantity of gas maintained at constant temperature (T) is inversely proportional to the pressure (P). 1 V P 1 V = constant P PV = constant (k)

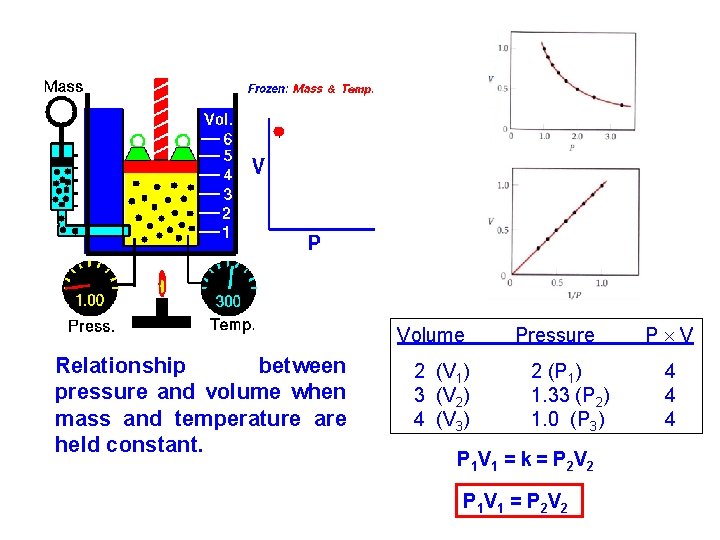
Volume Relationship between pressure and volume when mass and temperature are held constant. 2 (V 1) 3 (V 2) 4 (V 3) Pressure 2 (P 1) 1. 33 (P 2) 1. 0 (P 3) P 1 V 1 = k = P 2 V 2 P 1 V 1 = P 2 V 2 P V 4 4 4

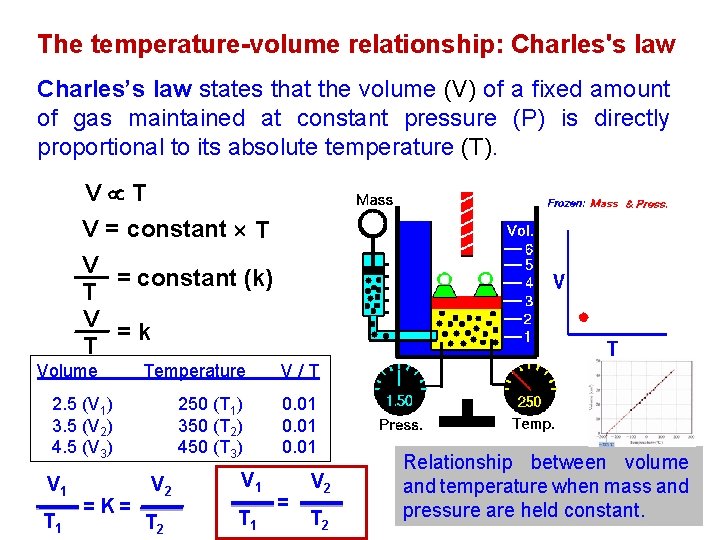
The temperature-volume relationship: Charles's law Charles’s law states that the volume (V) of a fixed amount of gas maintained at constant pressure (P) is directly proportional to its absolute temperature (T). V T V = constant (k) T V =k T Volume Temperature V/T 250 (T 1) 350 (T 2) 450 (T 3) 0. 01 2. 5 (V 1) 3. 5 (V 2) 4. 5 (V 3) V 1 T 1 = K= V 2 V 1 T 2 T 1 = V 2 T 2 Relationship between volume and temperature when mass and pressure are held constant.

The quantity-volume-amount relationship: Avogadro’s law Avogadro’s hypothesis: Equal volumes of gases at the same temperature and pressure contain equal numbers of molecules. Avogadro’s law: The volume (V) of a gas maintained at constant temperature (T) and pressure (P) is directly proportional to the number of moles (n) of the gas. V n V = constant n V=kn

10. 4 The ideal gas equation Boyle’s law : V 1 P (constant n, T) Chales’s law : V T (constant n, P) Avogadro’s law : V n (constant P, T) Combine all the three to form a single n. T V P If the proportionality constant is called "R", then it becomes: n. T V=R P Rearranging to a more familiar form: PV = n. RT ideal gas equation

• An "ideal gas" is one whose physical behavior is accurately described by the ideal-gas equation • The constant R is called the gas constant • The value and units of R depend on the units used in determining P, V, n and T • Temperature, T, must always be expressed on an kelvin temperature scale (K) • The quantity of gas, n, is normally expressed in moles • The units chosen for pressure and volume are typically atmospheres (atm) and liters (l), however, other units may be chosen • 273 K (0 C) and 1 atm are called standard temperature and pressure (STP)

Example: If a particular tennis ball has a volume of 144 cm 3 and contains 0. 33 g of N 2, what is the pressure inside the ball at 24 C? 144 cm 3 V= =0. 144 L 1000 1 mol N 2 n = 0. 33 g N 2 =0. 0118 mol 28 g N 2 T = 24 +273 =297 K R = 0. 08206 L-atom/mol-K P= n. RT V = P=? (0. 0118 mol) ( 0. 08206 L. atm / K. mol) (297 K) = 2 atm ( 0. 144 L )

Relating the ideal-gas equation and the gas laws PV = n. RT PV R= n. T P 2 V 2 P 1 V 1 =R= n 2 T 2 n 1 T 1 Usually amount of gas does not change, n 1 = n 2 P 2 V 2 P 1 V 1 = T 2 T 1 Combined gas law

Example 1: A gas initially at 4. 0 L, 1. 2 atm, and 66 C undergoes a change so that its final volume and temperature become 1. 7 L and 42 C. What is its final pressure ? Assume the number of moles remains unchanged P 1 V 1 T 1 P 2 V 2 = T 2 P 1= 1. 2 atm V 2= 1. 7 L T 2= 42+273 =315 K V 1= 4. 0 L T 1= 66+273 =339 K P 2= ? atm P 1 V 1 T 2 1. 2 atm 4. 0 L 315 K P 2 = = 339 K 1. 7 L T 1 V 2 = 2. 62 atm

10. 5 Further applications of the ideal-gas equation Gas densities and molar mass Density is defined as mass per unit volume m m = mass in gram d= V M = molar mass m number of mole, n = M Ideal gas equation, PV = n. RT PV n= RT PV m = M RT PM m = RT V d = PM RT or M = d. RT P

Example : Calculate the average molar mass of dry air if it has a density of 1. 17 g/L at 21 C and 740. 0 torr. M = d. RT P d = 1. 17 g/L P = 740. 0 torr= 740. 0/760 = 0. 974 atm T = (21+273)= 294 K R = 0. 0821 L. atm / K. mol M = d. RT P = 1. 17 g/L 0. 08206 L. atm/K. mol 294 K = 29. 28 g/mol 0. 974 atm

Volumes of gases in chemical reactions Example : Following the reaction if an air bag of has a volume of 36 L and is to be filled with nitrogen gas at a pressure of 1. 15 atom at a temperature of 26. 0 C, how many grams of Na. N 3 must be decomposed? 2 Na. N 3(s) 2 Na(s) + 3 N 2(g) V = 36. 0 L T = (26+273)= 299 K PV n= RT = P = 1. 15 atm R = 0. 0821 L. atm / K. mol (1. 15 atm 36. 0 L ( 0. 08206 L. atm / K. mol) 299 K ( ( = 1. 69 mol N 2 2 mol = 1. 12 Na. N 3 mol 3 N 2 Na. N 3 65 g Na. N 3 (1. 12 mol Na. N ) = 72. 8 Gram Na. N 3= 3 1 mol Na. N 3 Na. N ( ( Mole Na. N 3 = (1. 69 mol N 2) 3 mol g

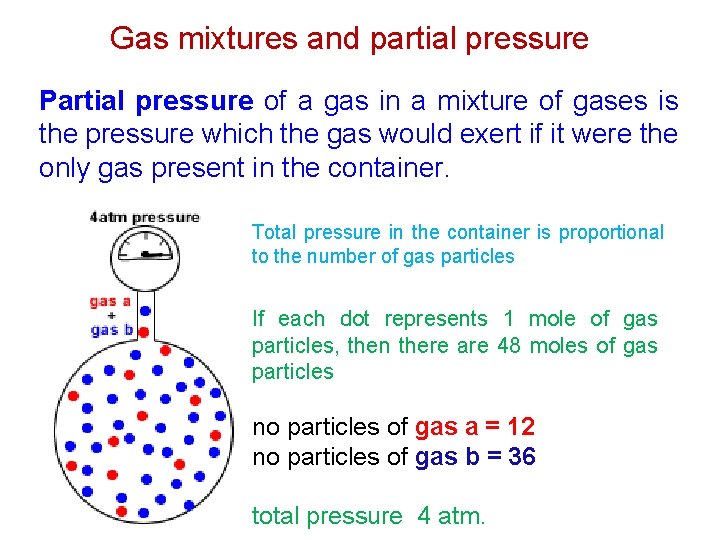
Gas mixtures and partial pressure Partial pressure of a gas in a mixture of gases is the pressure which the gas would exert if it were the only gas present in the container. Total pressure in the container is proportional to the number of gas particles If each dot represents 1 mole of gas particles, then there are 48 moles of gas particles no particles of gas a = 12 no particles of gas b = 36 total pressure 4 atm.

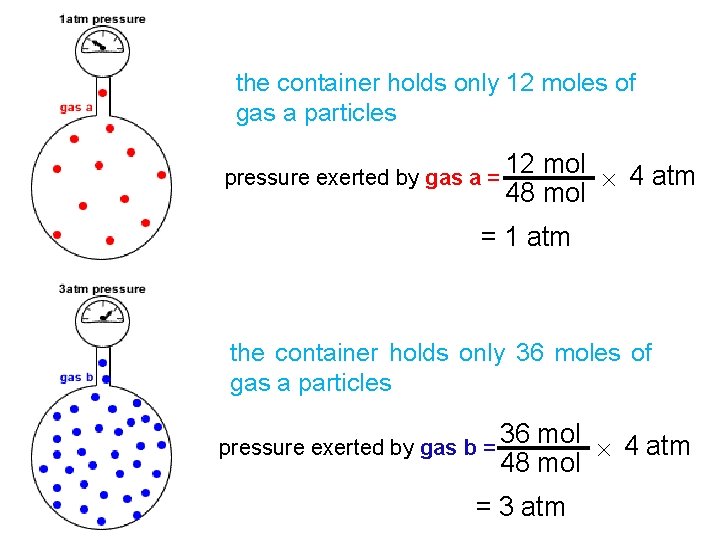
the container holds only 12 moles of gas a particles pressure exerted by gas a = 12 mol 4 atm 48 mol = 1 atm the container holds only 36 moles of gas a particles pressure exerted by gas b = 36 mol 4 atm 48 mol = 3 atm

Dalton’s Law of Partial Pressure Dalton's Law of Partial Pressures states that the total pressure of a mixture of gases equals the sum of the pressures that each would exert if it were present alone. Ptotal = = Pgas a + + Pgas b

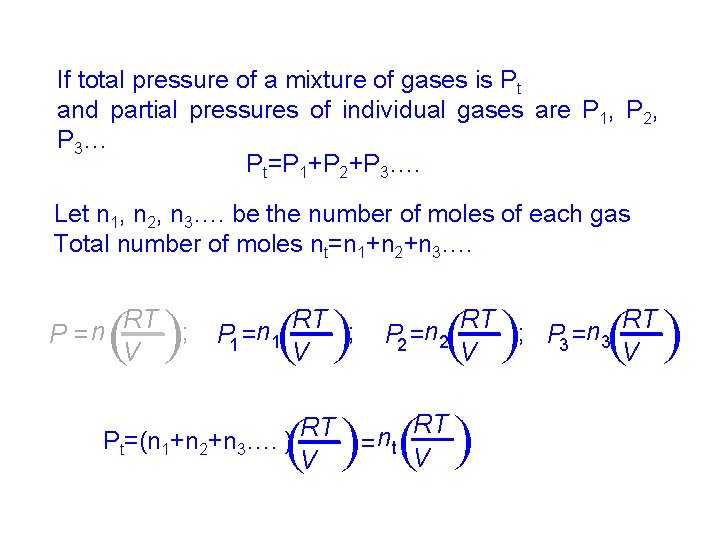
If total pressure of a mixture of gases is Pt and partial pressures of individual gases are P 1, P 2, P 3… Pt=P 1+P 2+P 3…. Let n 1, n 2, n 3…. be the number of moles of each gas Total number of moles nt=n 1+n 2+n 3…. ( RT n = t V ( ( ( RT Pt=(n 1+n 2+n 3…. ) V ( ( RT RT ; P 3 =n 3 P 2 =n 2 V V ( ( RT ; P 1 =n 1 V ( ( RT ; n P= V

Example : What is the total pressure exerted by a mixture of 2. 0 g of H 2 and 8. 0 g of N 2 at 273 K in a 10. 0 L velsel? Mole N 2 = (8. 0 g N 2) ( ( PH = n. H RT 2 2 V = ( ( 1 mol H 2 H 2 2 g ( ( Mole H 2 = (2. 0 g H 2) = 1 mol H 2 1 mol = 0. 286 mol N 28 g 2 N 2 (1 mol) ( 0. 08206 L. atm / K. mol) 273 K = 2. 24 atm 10. 0 L PN = n N RT = (0. 286 mol) ( 0. 08206 L. atm / K. mol) 273 K = 0. 64 atm 2 2 V 10. 0 L Pt= PH 2+ PN 2 = 2. 24 + 0. 64 = 2. 88 atm

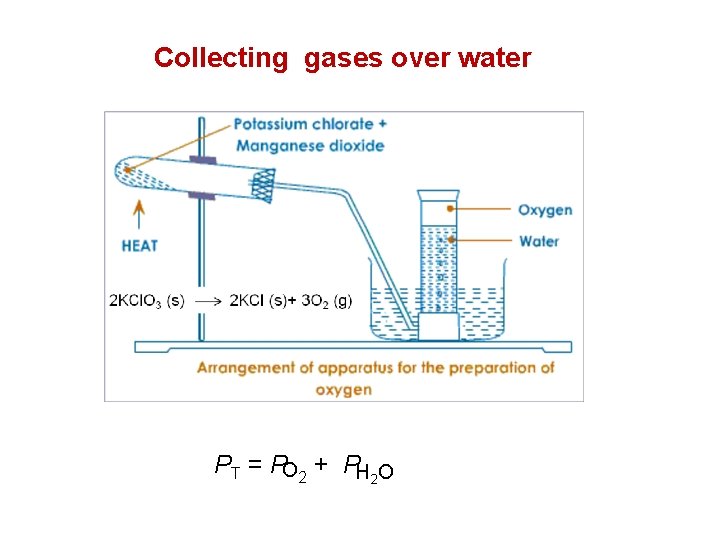
Collecting gases over water PT = PO 2 + PH 2 O

Example 2: Oxygen gas generated by the decomposition of potassium chlorate is collected over water. The volume of oxygen collected at 24 C and atmospheric pressure of 762 mm. Hg is 128 m. L. Calculate the mass (in grams) of oxygen gas obtained. The pressure of the water vapor at 24 C is 22. 4 mm. Hg. PT = PO 2 + PH 2 O P O 2 = P T - PH O = 762 mm. Hg – 22. 4 mm. Hg 2 =739. 6 mm. Hg = 739. 6 mm. Hg P = 0. 973 atm T = 273 + 24 = 297 K number of mole, n = V = 128 m. L = 0. 128 L M = molar mass = 32 g / mol R = 0. 08206 L. atm /K. mol m =mass in gram ? PV = n. RT = m= 1 atm = 0. 973 atm 760 mm. Hg m RT M PVM 0. 973 atm 0. 128 L 32 g / mol = 0. 163 g = RT 0. 0821 L. atm / K. mol 297 K m M