10 29 11 25 12 29 13 14

2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 2

PROPERTIES OF KITES AND TRAPEZOIDS Section 6 -5 Geometry Pre. AP, Revised © 2013

DEFINITIONS A. Kite is a quadrilateral with exactly two pairs of congruent consecutive sides.

PROPERTIES OF KITES A. A kite is a quadrilateral that has two pairs of

KITES If a quadrilateral is a kite, then the nonvertex angles are congruent. 2/19/2021

KITES If a quadrilateral is a kite, then the diagonal connecting the vertex angles

KITES If a quadrilateral is a kite, then a diagonal bisects the opposite non-congruent

EXAMPLE 1 In kite ABCD, m DAB = 54°, and m CDF = 52°.

EXAMPLE 2 In kite ABCD, m DAB = 54°, and m CDF = 52°.

YOUR TURN In kite PQRS, m PQR = 78°, and m TRS = 59°.

PROPERTIES OF TRAPEZOIDS A. The parallel sides are called bases B. The non-parallel sides

TRAPEZOIDS A. If a quadrilateral is a trapezoid, then the consecutive angles between the

MIDSEGMENT TRAPEZOIDS B. A midsegment of a trapezoid is a segment that connects the

TRAPEZOIDS C. If a trapezoid is isosceles, then each pair of base angles is

TRAPEZOIDS D. The midsegment of a trapezoid is parallel to each base and its

EXAMPLE 3 KP = 21. 9 m and FM = 32. 7 m. Solve

EXAMPLE 4 Find the value of a so that PQRS is isosceles. S P

YOUR TURN Find the value of x so that PQST is isosceles. 2/19/2021 6:

EXAMPLE 5 Find EH. 1 16. 5 = 2 (25 + EH) 33 =

YOUR TURN Solve for LP 2/19/2021 6: 36 PM 6 -5: Conditions of Special

ASSIGNMENT Pg 432: 14 -25, 27 -36 all (omit 34) 2/19/2021 6: 36 PM

Slides: 22

Download presentation

10) 29 11) 25 12) 29 13) 14. 5 14) 31. 5 PAGE 412 20) 21) 15) 18) 22) 19) 24) Always 25) Sometimes 26) Sometimes 27) Sometimes 28) Always 29) Always 30) Always 31) Sometimes 23) 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 1

2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 2

DEFINITIONS A. Kite is a quadrilateral with exactly two pairs of congruent consecutive sides. B. Trapezoid is a quadrilateral with exactly one pair of parallel sides 1. Each parallel side is called a base 2. Base angles of a trapezoid are two consecutive angles whose common side is a base 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 4

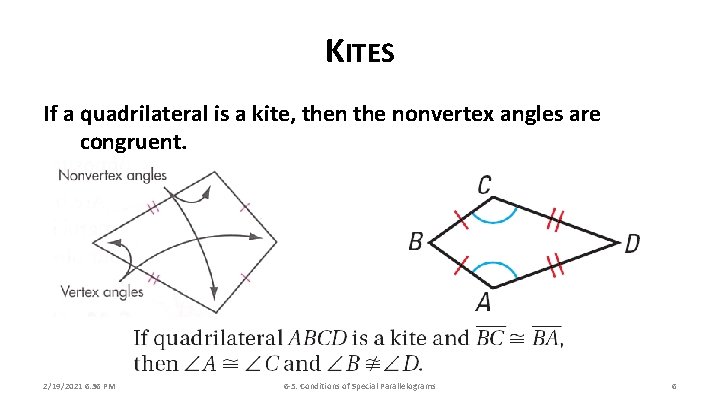
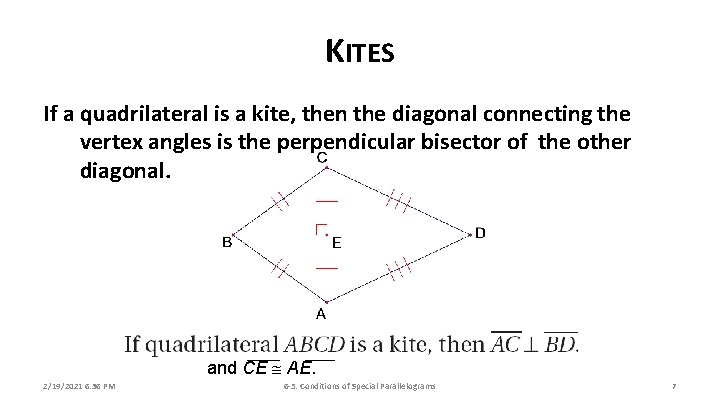
PROPERTIES OF KITES A. A kite is a quadrilateral that has two pairs of consecutive congruent sides, but opposite sides are not congruent. B. Just as in an isosceles triangle, the angles between each pair of congruent sides are vertex angles. The other pair of angles are nonvertex angles. C. If a quadrilateral is a kite, then its diagonals are perpendicular D. If a quadrilateral is a kite, then exactly one pair of opposite angles are congruent 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 5

KITES If a quadrilateral is a kite, then the nonvertex angles are congruent. 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 6

KITES If a quadrilateral is a kite, then the diagonal connecting the vertex angles is the perpendicular bisector of the other diagonal. and CE AE. 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 7

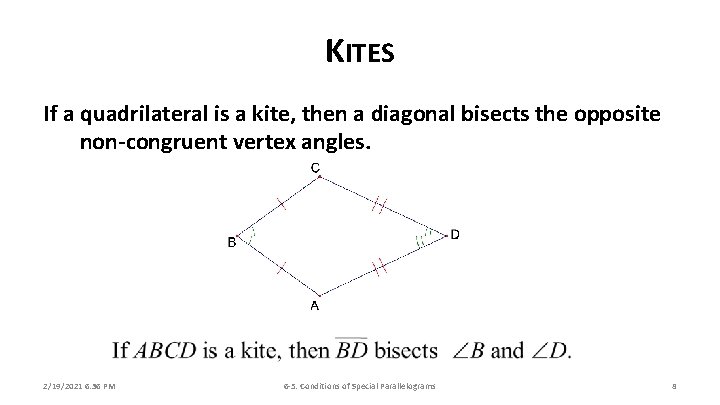
KITES If a quadrilateral is a kite, then a diagonal bisects the opposite non-congruent vertex angles. 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 8

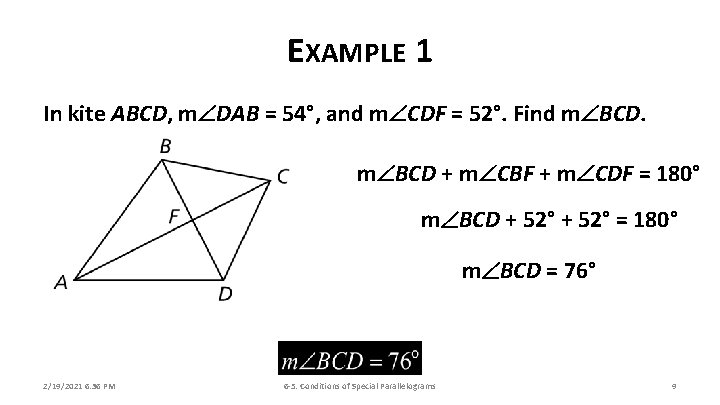
EXAMPLE 1 In kite ABCD, m DAB = 54°, and m CDF = 52°. Find m BCD + m CBF + m CDF = 180° m BCD + 52° = 180° m BCD = 76° 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 9

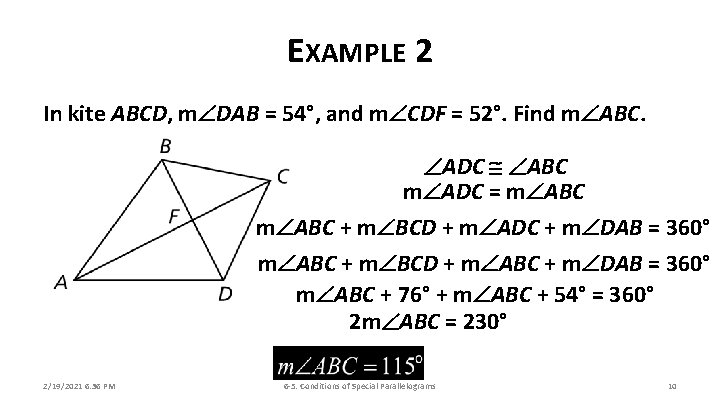
EXAMPLE 2 In kite ABCD, m DAB = 54°, and m CDF = 52°. Find m ABC. ADC ABC m ADC = m ABC + m BCD + m ADC + m DAB = 360° m ABC + m BCD + m ABC + m DAB = 360° m ABC + 76° + m ABC + 54° = 360° 2 m ABC = 230° 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 10

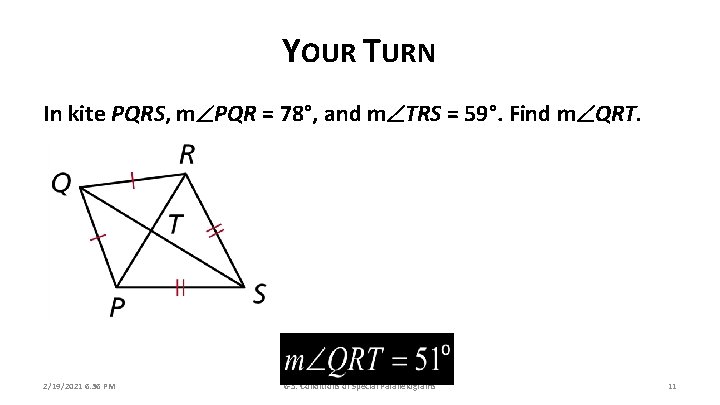
YOUR TURN In kite PQRS, m PQR = 78°, and m TRS = 59°. Find m QRT. 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 11

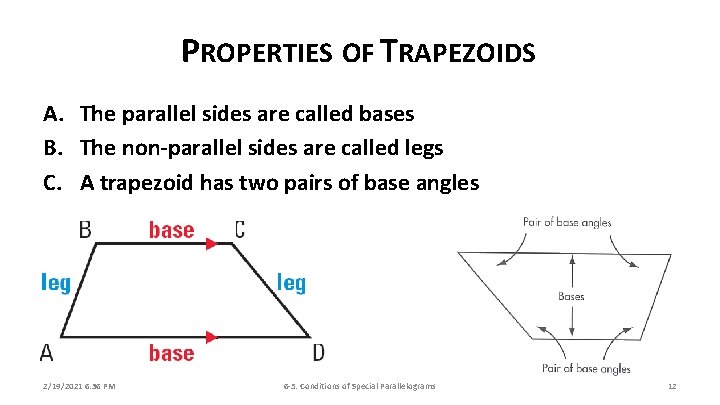
PROPERTIES OF TRAPEZOIDS A. The parallel sides are called bases B. The non-parallel sides are called legs C. A trapezoid has two pairs of base angles 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 12

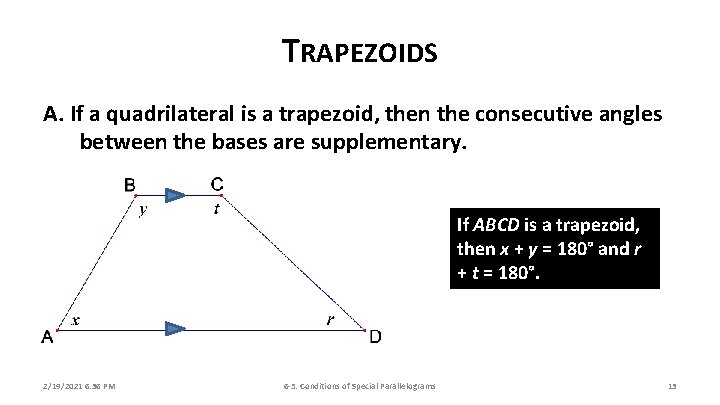
TRAPEZOIDS A. If a quadrilateral is a trapezoid, then the consecutive angles between the bases are supplementary. If ABCD is a trapezoid, then x + y = 180° and r + t = 180°. 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 13

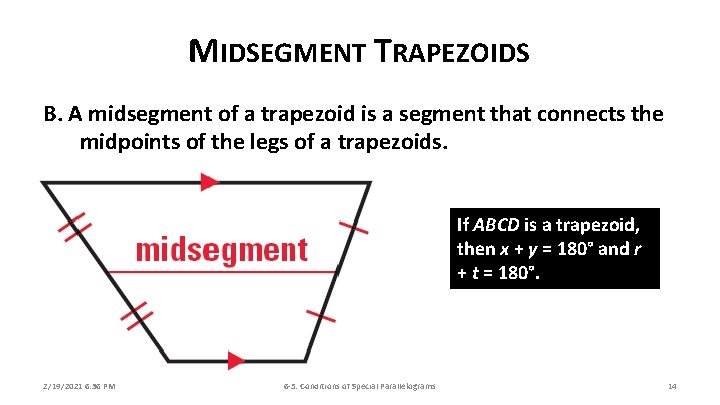
MIDSEGMENT TRAPEZOIDS B. A midsegment of a trapezoid is a segment that connects the midpoints of the legs of a trapezoids. If ABCD is a trapezoid, then x + y = 180° and r + t = 180°. 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 14

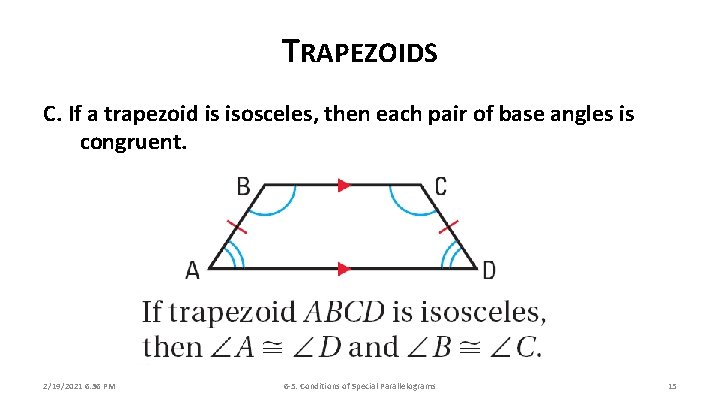
TRAPEZOIDS C. If a trapezoid is isosceles, then each pair of base angles is congruent. 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 15

TRAPEZOIDS D. The midsegment of a trapezoid is parallel to each base and its length is one half the sum of the lengths of the bases. If 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 16

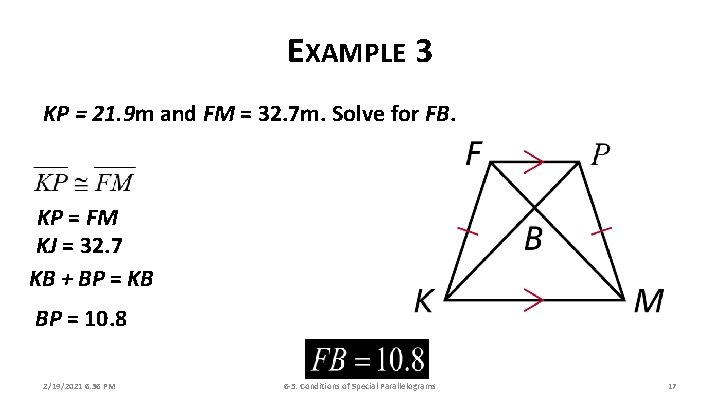
EXAMPLE 3 KP = 21. 9 m and FM = 32. 7 m. Solve for FB. KP = FM KJ = 32. 7 KB + BP = KB BP = 10. 8 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 17

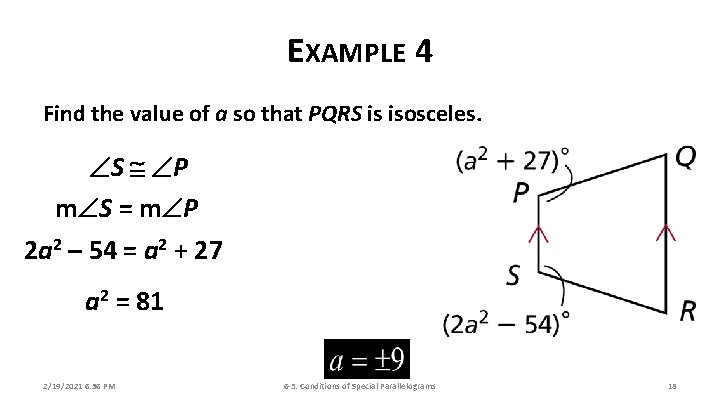
EXAMPLE 4 Find the value of a so that PQRS is isosceles. S P m S = m P 2 a 2 – 54 = a 2 + 27 a 2 = 81 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 18

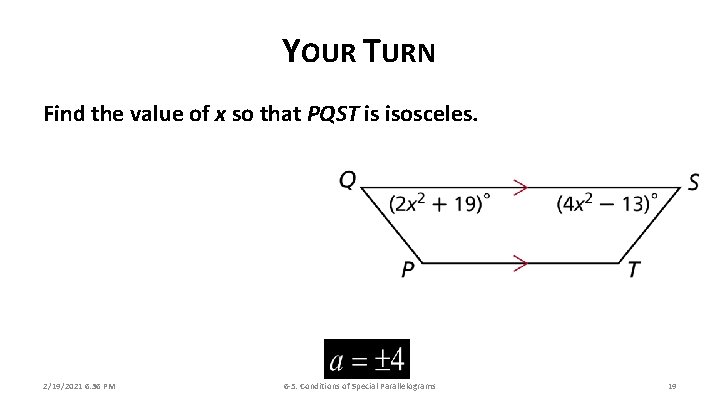
YOUR TURN Find the value of x so that PQST is isosceles. 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 19

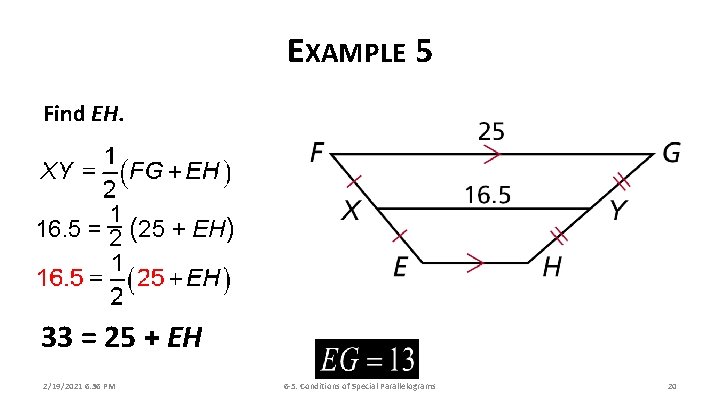
EXAMPLE 5 Find EH. 1 16. 5 = 2 (25 + EH) 33 = 25 + EH 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 20

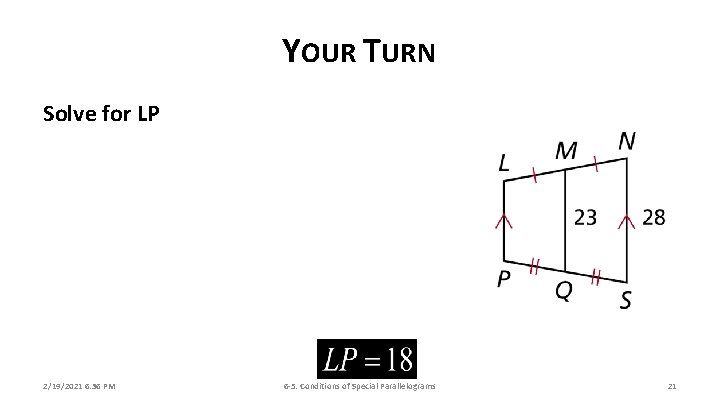
YOUR TURN Solve for LP 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 21

ASSIGNMENT Pg 432: 14 -25, 27 -36 all (omit 34) 2/19/2021 6: 36 PM 6 -5: Conditions of Special Parallelograms 22