10 2 Stationary waves on a stretched string

10. 2 Stationary waves on a stretched string © Manhattan Press (H. K. ) Ltd. 1

10. 2 Stationary waves on a stretched string (SB p. 131) Stationary waves on a stretched string Stringed instruments sound by - resonance of stretched strings © Manhattan Press (H. K. ) Ltd. 2

10. 2 Stationary waves on a stretched string (SB p. 131) Stationary waves on a stretched string Note: 1. The nature and speed of waves formed in strings are different from those formed in air. The waves formed in strings are transverse waves, while those formed in air are longitudinal waves. 2. Stationary waves can be formed in stretched strings and closed/open pipes. Once they propagate into the air, they become progressive waves. Both the speed and wavelength are changed. Only their frequency remains unchanged. © Manhattan Press (H. K. ) Ltd. 3

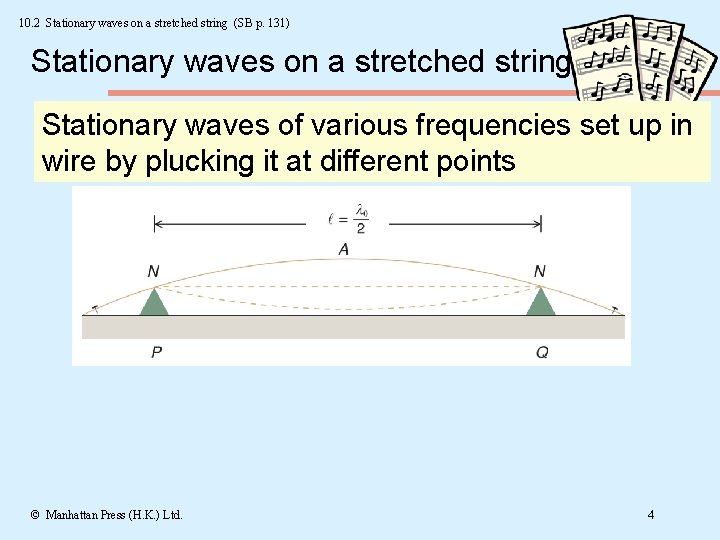
10. 2 Stationary waves on a stretched string (SB p. 131) Stationary waves on a stretched string Stationary waves of various frequencies set up in wire by plucking it at different points © Manhattan Press (H. K. ) Ltd. 4

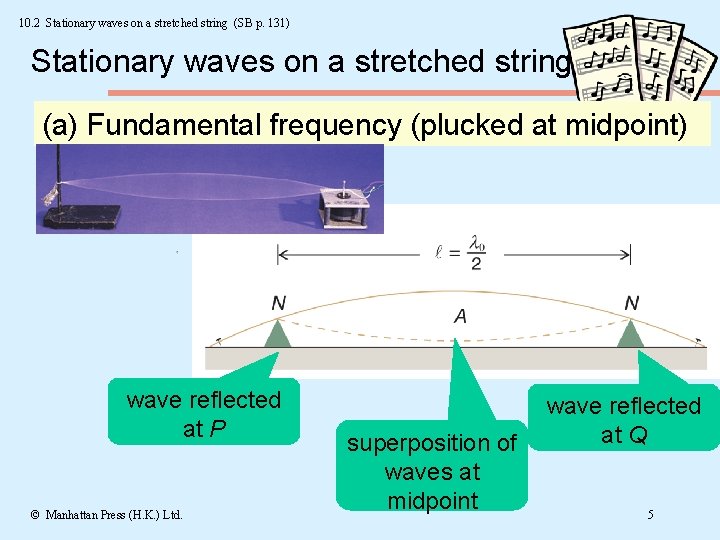
10. 2 Stationary waves on a stretched string (SB p. 131) Stationary waves on a stretched string (a) Fundamental frequency (plucked at midpoint) wave reflected at P © Manhattan Press (H. K. ) Ltd. superposition of waves at midpoint wave reflected at Q 5

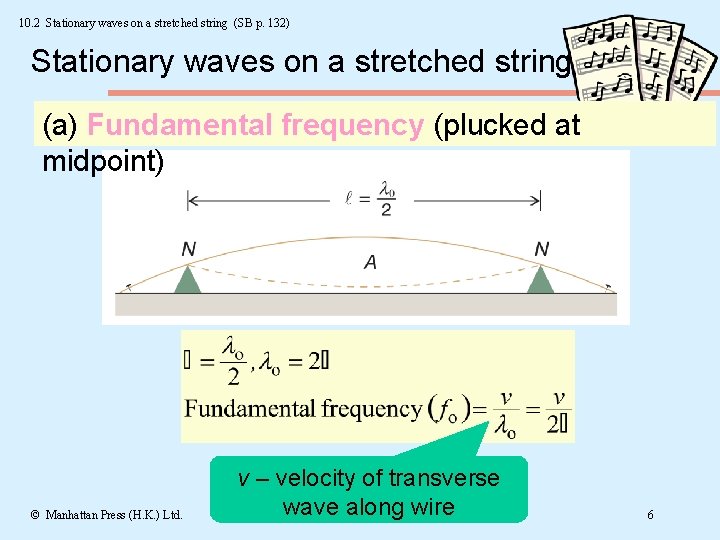
10. 2 Stationary waves on a stretched string (SB p. 132) Stationary waves on a stretched string (a) Fundamental frequency (plucked at midpoint) © Manhattan Press (H. K. ) Ltd. v – velocity of transverse wave along wire 6

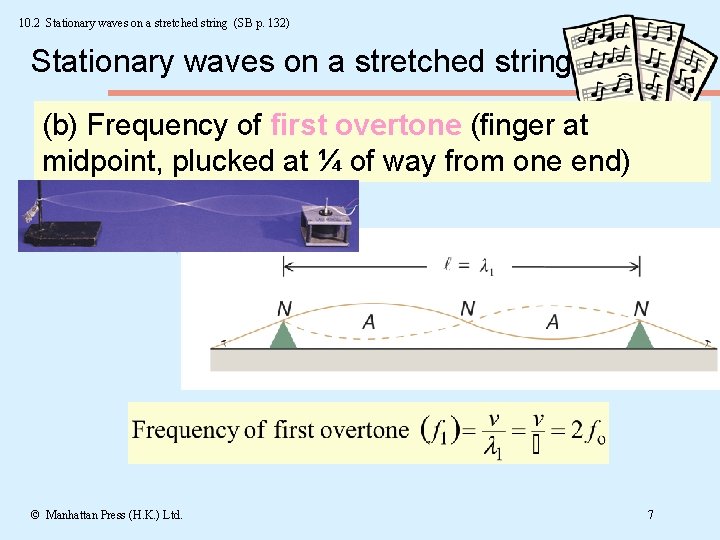
10. 2 Stationary waves on a stretched string (SB p. 132) Stationary waves on a stretched string (b) Frequency of first overtone (finger at midpoint, plucked at ¼ of way from one end) © Manhattan Press (H. K. ) Ltd. 7

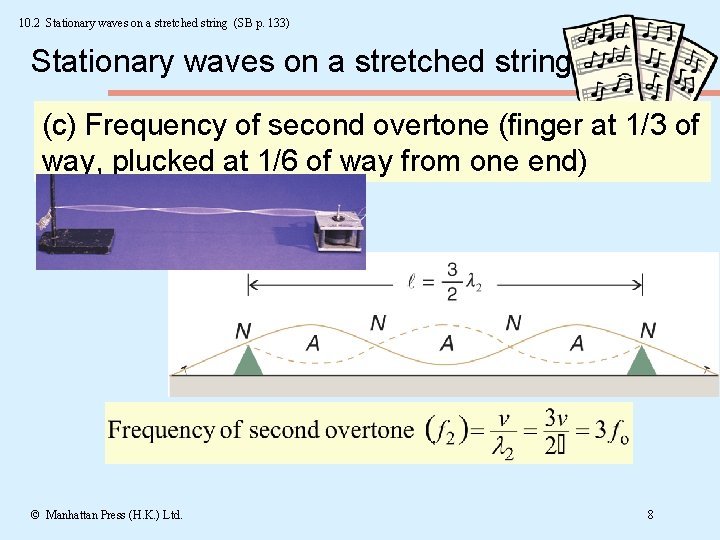
10. 2 Stationary waves on a stretched string (SB p. 133) Stationary waves on a stretched string (c) Frequency of second overtone (finger at 1/3 of way, plucked at 1/6 of way from one end) © Manhattan Press (H. K. ) Ltd. 8

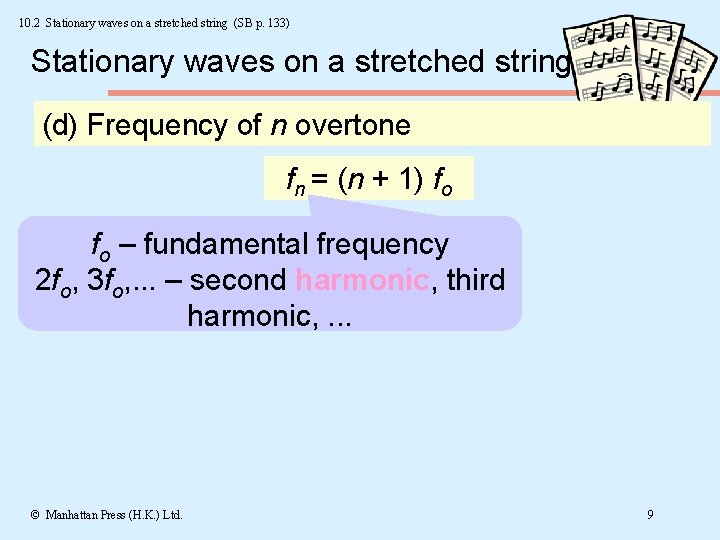
10. 2 Stationary waves on a stretched string (SB p. 133) Stationary waves on a stretched string (d) Frequency of n overtone fn = (n + 1) fo fo – fundamental frequency 2 fo, 3 fo, . . . – second harmonic, third harmonic, . . . © Manhattan Press (H. K. ) Ltd. 9

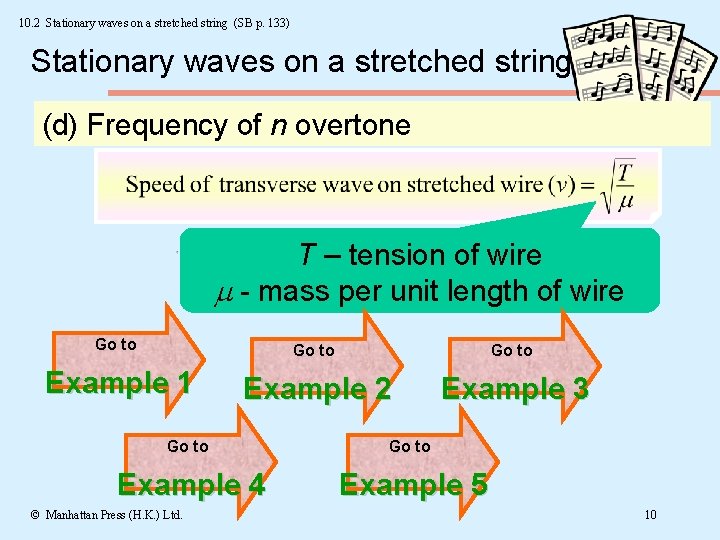
10. 2 Stationary waves on a stretched string (SB p. 133) Stationary waves on a stretched string (d) Frequency of n overtone T – tension of wire - mass per unit length of wire Go to Example 1 Example 2 Example 3 Go to Example 4 Example 5 © Manhattan Press (H. K. ) Ltd. 10

End © Manhattan Press (H. K. ) Ltd. 11

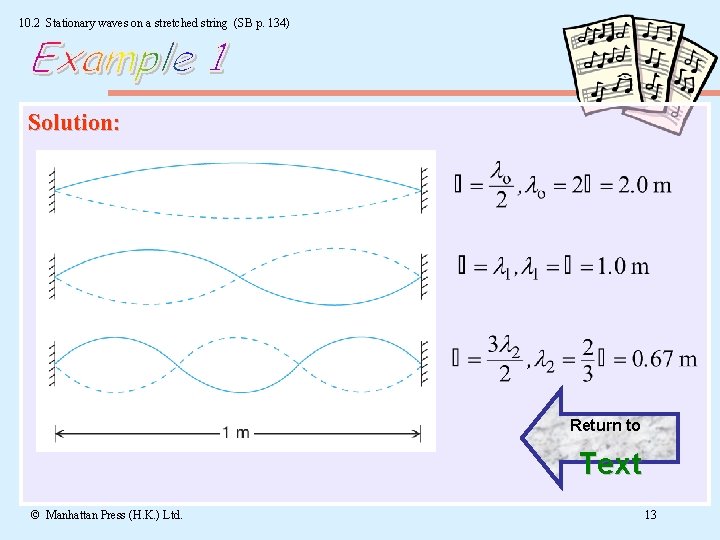
10. 2 Stationary waves on a stretched string (SB p. 134) Q: A wire stretched between two points 1. 0 m apart is plucked near one end. What will be three longest wavelengths shown on the vibrating wire? Solution © Manhattan Press (H. K. ) Ltd. 12

10. 2 Stationary waves on a stretched string (SB p. 134) Solution: Return to Text © Manhattan Press (H. K. ) Ltd. 13

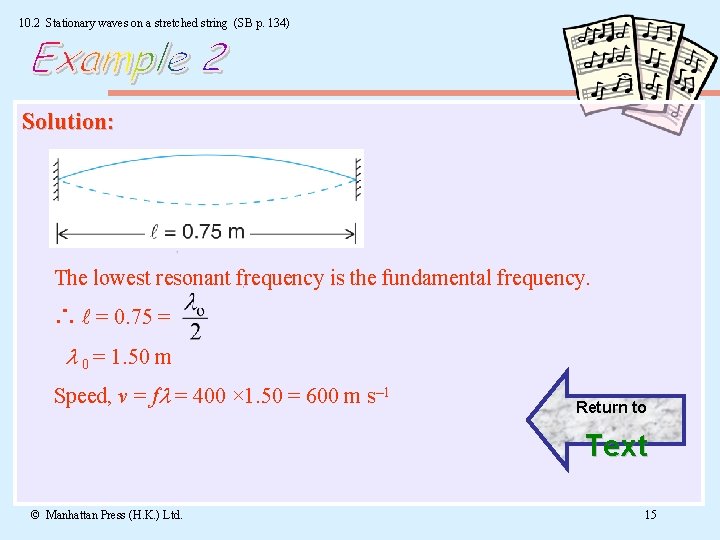
10. 2 Stationary waves on a stretched string (SB p. 134) Q: The lowest resonant frequency for a guitar string of length 0. 75 m is 400 Hz. Calculate the speed of a transverse wave on the string. Solution © Manhattan Press (H. K. ) Ltd. 14

10. 2 Stationary waves on a stretched string (SB p. 134) Solution: The lowest resonant frequency is the fundamental frequency. ∴ l = 0. 75 = 0 = 1. 50 m Speed, v = f = 400 × 1. 50 = 600 m s– 1 Return to Text © Manhattan Press (H. K. ) Ltd. 15

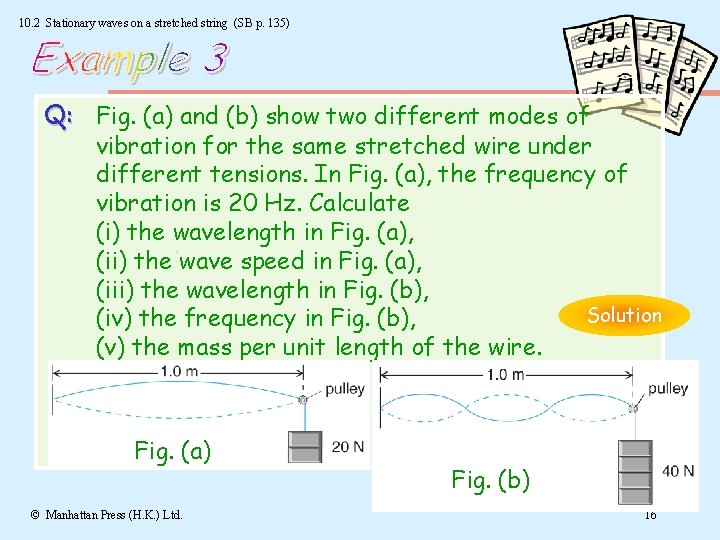
10. 2 Stationary waves on a stretched string (SB p. 135) Q: Fig. (a) and (b) show two different modes of vibration for the same stretched wire under different tensions. In Fig. (a), the frequency of vibration is 20 Hz. Calculate (i) the wavelength in Fig. (a), (ii) the wave speed in Fig. (a), (iii) the wavelength in Fig. (b), Solution (iv) the frequency in Fig. (b), (v) the mass per unit length of the wire. Fig. (a) © Manhattan Press (H. K. ) Ltd. Fig. (b) 16

10. 2 Stationary waves on a stretched string (SB p. 135) Solution: Return to Text © Manhattan Press (H. K. ) Ltd. 17

10. 2 Stationary waves on a stretched string (SB p. 136) Q: The key on a piano corresponding to a note of frequency 440 Hz is pressed down very lightly so that the string is free to vibrate. When the key corresponding to a note of frequency 220 Hz is struck, it is found that the 440 Hz string emits a note of frequency 220 Hz. (a) Explain briefly the observation. (b) If the 110 Hz string is also free to vibrate, what frequencies, if any, would it Solution emit when the 220 Hz key is struck? © Manhattan Press (H. K. ) Ltd. 18

10. 2 Stationary waves on a stretched string (SB p. 136) Solution: (a) When the key corresponding to the frequency of 220 Hz is struck, the 440 Hz string is forced into vibration. It vibrates with the same frequency as that which causes the vibration. Hence a note of frequency 220 Hz is emitted. (b) If the 110 Hz string is free to vibrate, it would also be forced into vibrating with the forced frequency 220 Hz or multiples of this frequency, i. e. 440 Hz, 660 Hz, . . . Return to Text © Manhattan Press (H. K. ) Ltd. 19

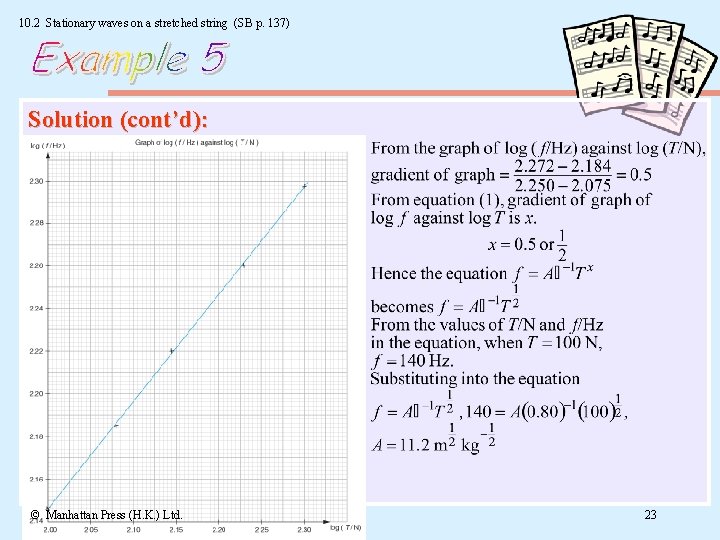
10. 2 Stationary waves on a stretched string (SB p. 136) Q: The fundamental frequency of vibration f of a wire of length l stretched by a force T is given by f = Al – 1 T x where A is a constant characteristic of the wire. The following readings of f were obtained for a wire of length 0. 80 m under the tensions T stated. T/N f/Hz 100 140 120 153 140 166 170 182 200 198 (a) Explain briefly one method of measuring such frequencies without using a tuning fork. (b) By a graphical method, or otherwise, find the values of A and x in the equation. © Manhattan Press (H. K. ) Ltd. 20

10. 2 Stationary waves on a stretched string (SB p. 137) Q: The same wire was attached at one end to a vibrator, the arm of which produced a small transverse motion. The other end passed over a pulley so that the length of wire between the vibrator arm and the pulley was 0. 80 m. A mass of 16 kg was attached to the free end of the wire. It was found that for a number of frequencies of the vibrator, the wire vibrated with large amplitude at certain points along its length. (c) Explain briefly why this happened. (d) Find the three lowest frequencies at which the effect was observed, and sketch the appearance of the vibrating wire in each case. © Manhattan Press (H. K. ) Ltd. 21 Solution

10. 2 Stationary waves on a stretched string (SB p. 137) Solution: (a) The frequency f can be measured using a xenon stroboscope. The frequency of the xenon stroboscope is increased from zero until the vibration of the wire is frozen. When this happens, the frequency of the vibration of the wire f is equal to the frequency of the stroboscope. (b) We have: f = Al – 1 Tx Taking log, log f = log (Al – 1 ) + x log T. . . (1) log (T/N) 2. 000 2. 079 2. 146 2. 230 2. 301 log (f/Hz) 2. 146 2. 185 2. 220 2. 260 2. 297 © Manhattan Press (H. K. ) Ltd. 22

10. 2 Stationary waves on a stretched string (SB p. 137) Solution (cont’d): © Manhattan Press (H. K. ) Ltd. 23

10. 2 Stationary waves on a stretched string (SB p. 139) Return to Solution (cont’d): Text (c) When the end of the wire attached to the vibrator vibrates, a transverse wave travels along the wire to the other end. At the pulley, the wave is reflected. The superposition of the incident and reflected waves produces a stationary wave on the stretched wire. The lowest frequency of the vibrator when this occurs (fo) = v/2 l where v = speed of the transverse wave along the wire and l = length of the wire. Other frequencies when this occurs are 2 fo, 3 fo, . . . (d) The fundamental frequency is given by The frequencies of the first and second overtones are 354 Hz and 531 Hz respectively. © Manhattan Press (H. K. ) Ltd. 24