10 2 Arithmetic Sequences Series Objectives Find nth

10. 2 Arithmetic Sequences & Series Objectives: -Find nth terms and arithmetic means of arithmetic sequences - Find sums of n terms of arithmetic series

Recursive Formula �

Definitions Arithmetic sequence: when the difference between consecutive terms is constant. Common Difference: denoted d, the constant difference between terms. *To find the common difference, subtract any term from its previous term. * To find the next term in the sequence, ADD the common difference to the given term.

Example 1: Determine the common difference and the next four terms of the arithmetic sequence. A)– 53, – 36, – 19, …. …. B) 74, 68, 62, 56,

Equations �

Example 2: Find both an explicit formula and a recursive formula for the nth term of the arithmetic sequence. A) 14, 3, – 8, …. B) 15, 33, 51, ….

Example 3: A) Find the 41 st term of the arithmetic sequence 11, 4, – 3, – 10, ….

Example 3: B) Find the first term of the arithmetic sequence for which a 44 = 229 and d = 8.

Example 3: C) Find d of the arithmetic sequence for which a 1 = 75 and a 38 = 56. 5 D) Find n if an = 336, a 1 = 18, and d = 6.

Example 3: E) Given a 8 = 25 and a 20 = 61, find a 53 for the arithmetic sequence.

Arithmetic Mean �

Example 4: A) Write an arithmetic sequence that has five arithmetic means between 6. 2 and – 1. 6.

Example 4: B) Write an arithmetic sequence that has five arithmetic means between 16. 2 and 14. 7.

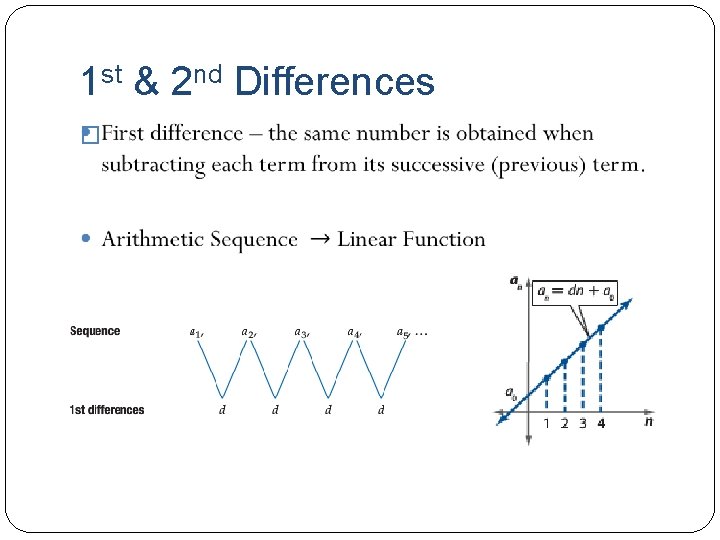
1 st & 2 nd Differences �

1 st & 2 nd Differences �If first differences are NOT the same, then not arithmetic. �Second difference – the same number is obtained when consecutive first differences are subtracted from one another. �Quadratic Function

Example 5: A) Find a quadratic model for the sequence 0, 5, 12, 21, 32, 45, ….

Example 5: B) Find a quadratic model for the sequence 10, 14, 22, 34, 50, ….

Arithmetic Series - The indicated sum of the terms of an arithmetic sequence. Sequence: 1, 2, 3, 4 4 Series: 1 + 2 + 3 +

Example 6: A) Find the sum of – 3 + 2 + 7 + 12 + … + 157.

Example 6: B) Find the 17 th partial sum of the arithmetic series 53 + 31 + 9 + ….

Example 6: C)

Example 7: A) An artist receives royalties for all CDs of his music that are sold. For the first 10, 000 CDs sold, the artist receives $10, 000. He receives $12, 500 for the next 10, 000 CDs, $15, 000 for the next 10, 000 CDs, and so on. How much money will he receive in total, if 500, 000 of his CDs are sold?

Example 7: B) A toy manufacturer wants to make a profit of $50, 000 the first year, $62, 000 the second year, $74, 000 the third year, and so on. His goal is to make a profit of at least $500, 000 selling toys. How many years will it take for the manufacturer to reach his goal?

Example 8: SALES Anna sells clothing in a store at a mall. Her commission on the sale of new seasonal merchandise is $3. 50 per item costing at least $25. To encourage an increase in sales, the store manager promises a $0. 05 increase in commission for each additional item sold. Thus, on the sale of the next item, Anna will earn $3. 55 in commission. On the sale of the third item, Anna will earn $3. 60, and so on. How many items worth $25 or more will Anna need to sell for her total commission on new merchandise to be at least $1000?

Example 9: Consider the arithmetic series 20 + 18 + 16 + 14 + …. a) Write the series using summation notation. b) Find S 25 c) Find n such that Sn = – 760

Example 10: Consider the arithmetic series 100 + 110 + 120 + 130 + … a) Write the series using summation notation. b) Find S 18 = 600 c) Find n such that Sn

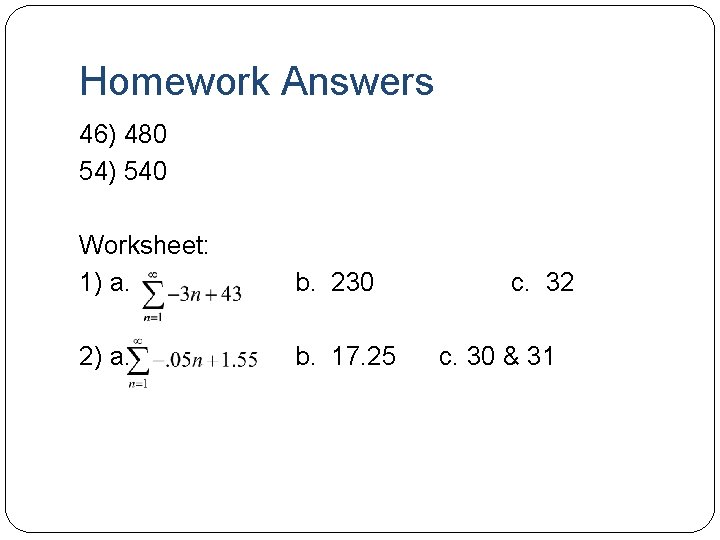
Homework Answers 46) 480 54) 540 Worksheet: 1) a. b. 230 2) a. b. 17. 25 c. 32 c. 30 & 31