10 1 RightAngle Trigonometry Warm Up Given the

10 -1 Right-Angle Trigonometry Warm Up Given the measure of one of the acute angles in a right triangle, find the measure of the other acute angle. 1. 45° 2. 60° 3. 24° 4. 38° Find the unknown length for each right triangle with legs a and b and hypotenuse c. 5. b = 12, c =13 6. a = 3, b = 3 Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry Holt Mc. Dougal Algebra 2

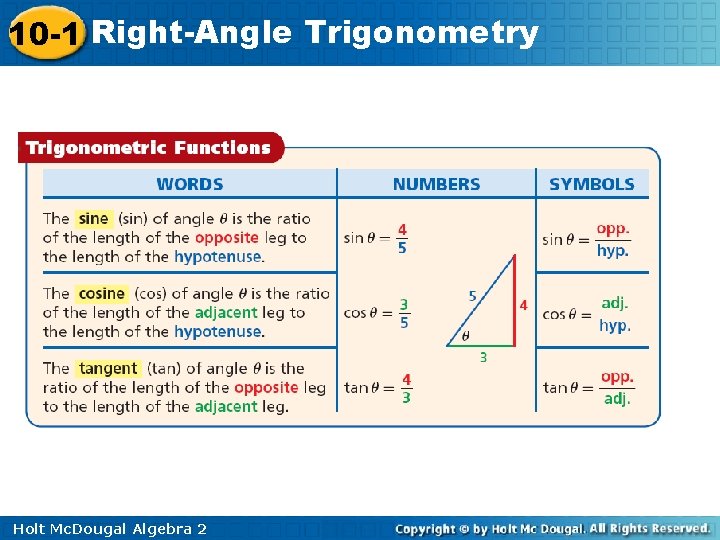
10 -1 Right-Angle Trigonometry The triangle shown at right is similar to the one in the table because their corresponding angles are congruent. No matter which triangle is used, the value of sin θ is the same. The values of the sine and other trigonometric functions depend only on angle θ and not on the size of the triangle. Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry Example 1: Finding Trigonometric Ratios Find the value of the sine, cosine, and tangent functions for θ. sin θ = cos θ = tan θ = Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry Check It Out! Example 1 Find the value of the sine, cosine, and tangent functions for θ. sin θ = cos θ = tan θ = Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry Example 2: Finding Side Lengths of Special Right Triangles Use a trigonometric function to find the value of x. ° The sine function relates the opposite leg and the hypotenuse. Substitute 30° for θ, x for opp, and 74 for hyp. Substitute x = 37 Holt Mc. Dougal Algebra 2 for sin 30°. Multiply both sides by 74 to solve for x.

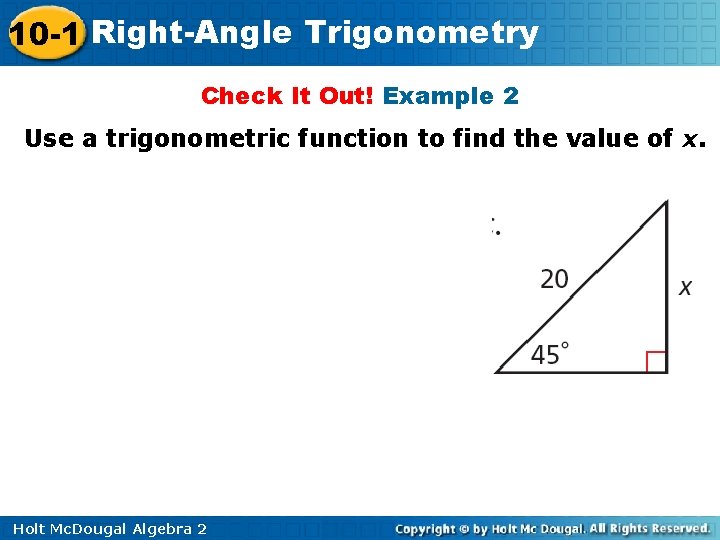
10 -1 Right-Angle Trigonometry Check It Out! Example 2 Use a trigonometric function to find the value of x. Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry Example 3: Sports Application In a waterskiing competition, a jump ramp has the measurements shown. To the nearest foot, what is the height h above water that a skier leaves the ramp? Substitute 15. 1° for θ, h for opp. , and 19 for hyp. 5≈h Multiply both sides by 19. Use a calculator to simplify. The height above the water is about 5 ft. Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry Check It Out! Example 3 A skateboard ramp will have a height of 12 in. , and the angle between the ramp and the ground will be 17°. To the nearest inch, what will be the length l of the ramp? Holt Mc. Dougal Algebra 2

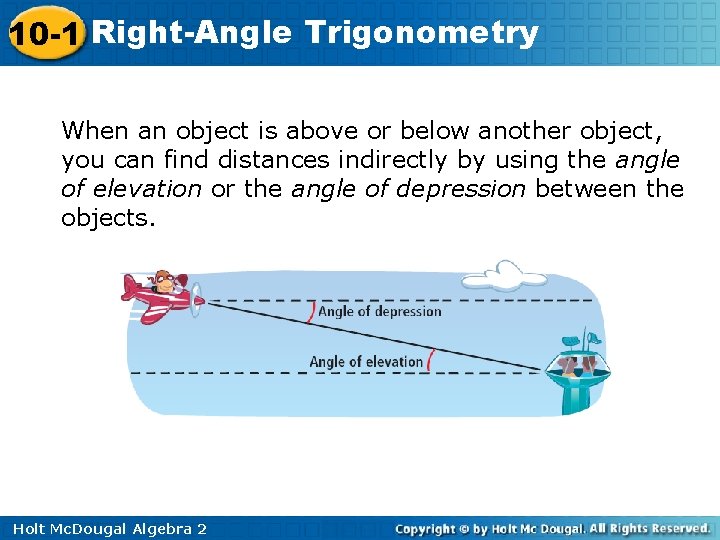
10 -1 Right-Angle Trigonometry When an object is above or below another object, you can find distances indirectly by using the angle of elevation or the angle of depression between the objects. Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry Example 4: Geology Application A biologist whose eye level is 6 ft above the ground measures the angle of elevation to the top of a tree to be 38. 7°. If the biologist is standing 180 ft from the tree’s base, what is the height of the tree to the nearest foot? Step 1 Draw and label a diagram to represent the information given in the problem. Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry Example 4 Continued Step 2 Let x represent the height of the tree compared with the biologist’s eye level. Determine the value of x. Use the tangent function. Substitute 38. 7 for θ, x for opp. , and 180 for adj. 180(tan 38. 7°) = x 144 ≈ x Multiply both sides by 180. Use a calculator to solve for x. Step 3 Determine the overall height of the tree. x + 6 = 144 + 6 = 150 The height of the tree is about 150 ft. Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry Check It Out! Example 4 A surveyor whose eye level is 6 ft above the ground measures the angle of elevation to the top of the highest hill on a roller coaster to be 60. 7°. If the surveyor is standing 120 ft from the hill’s base, what is the height of the hill to the nearest foot? Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry The reciprocals of the sine, cosine, and tangent ratios are also trigonometric ratios. They are trigonometric functions, cosecant, and cotangent. Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry Example 5: Finding All Trigonometric Functions Find the values of the six trigonometric functions for θ. Step 1 Find the length of the hypotenuse. c 2 = 242 + 702 Pythagorean Theorem. Substitute 24 for a and 70 for b. c 2 = 5476 Simplify. a 2 + b 2 = c 2 c = 74 Holt Mc. Dougal Algebra 2 70 Solve for c. Eliminate the negative solution. θ 24

10 -1 Right-Angle Trigonometry Example 5 Continued Step 2 Find the function values. Holt Mc. Dougal Algebra 2

10 -1 Right-Angle Trigonometry Check It Out! Example 5 Find the values of the six trigonometric functions for θ. 80 θ 18 Holt Mc. Dougal Algebra 2