10 1 Infinite Sequences and Summation Notation Find

10. 1 Infinite Sequences and Summation Notation · Find terms of sequences given the general or nth term. ·Convert between sigma notation and other notation for a series.

Sequences l A sequence is a function. l An infinite sequence is a function {1, 2, 3, 4, 5, …}. l A finite sequence is a function {1, 2, 3, 4, 5, …, n}, for some positive integer n.

Sequence Formulas l In a formula, the function values are known as terms of the sequence. ¡The first term in a sequence is denoted as a 1, ¡the third term as a 3 , ¡and the nth term, or the general term, as an.

Example l Find the first 4 terms and the 9 th term of the sequence whose general term is given by an = 4( 2)n. Solution: We have an = 4( 2)n, so a 1 = 4( 2)1 = 8 a 2 = 4( 2)2 = 16 a 3 = 4( 2)3 = 32 a 4 = 4( 2)4 = 64 a 9 = 4( 2)9 = 2048 The power ( 2)n causes the sign of the terms to alternate between positive and negative, depending on whether the n is even or odd. This kind of sequence is called an alternating sequence.

Sigma Notation l The Greek letter (sigma) can be used to simplify notation when the general term of a sequence is a formula. For example, the sum of the first three terms of the sequence l , …, , … can be named as follows, using sigma notation, or summation notation:

Sigma Notation l This is read “the sum as k goes from 1 to 3 of l The letter k is called the index of summation. The index of summation might be a number other than 1, and a letter other than k can be used.

Example l Find the sum. Solution: k = 2 k = 3 k = 4 ( 1)232 + ( 1)333 + ( 1)434 = 9 + ( 27) + 81 = 63

• Find the sum. k = 4 k = 5 k = 6 k = 7 k = 8

10. 2 Arithmetic Sequences and Series

Sequences and Summations l A sequence is an ordered list, possibly infinite, of elements. l We will use the following notation: a 1, a 2, a 3, . . . l We also refer to the elements of the sequence as terms, and if ak is a term, then k is its index or subscript.

Arithmetic Sequences and Series Arithmetic Sequence: sequence whose consecutive terms have a common difference. Example: 3, 5, 7, 9, 11, 13, . . . The terms have a common difference of 2. The common difference is the number d. Example: Is the sequence arithmetic? – 45, – 30, – 15, 0, 15, 30 Yes, the common difference is 15 How do you find any term in this sequence? To find any term in an arithmetic sequence, use the formula an = a 1 + (n – 1)d where d is the common difference.

Example: Find a formula for the nth term of the arithmetic sequence in which the common difference is 5 and the first term is 3. an = a 1 + (n – 1)d a 1 = 3 d = 5 an = 3 + (n – 1)5

Example: If the common difference is 4 and the fifth term is 15, what is the 10 th term of an arithmetic sequence? an = a 1 + (n – 1)d We need to determine what the first term is. . . d = 4 and a 5 = 15 a 5 = a 1 + (5 – 1)4 = 15 a 1 = – 1 a 10 = – 1 + (10 – 1)4 a 10 = 35

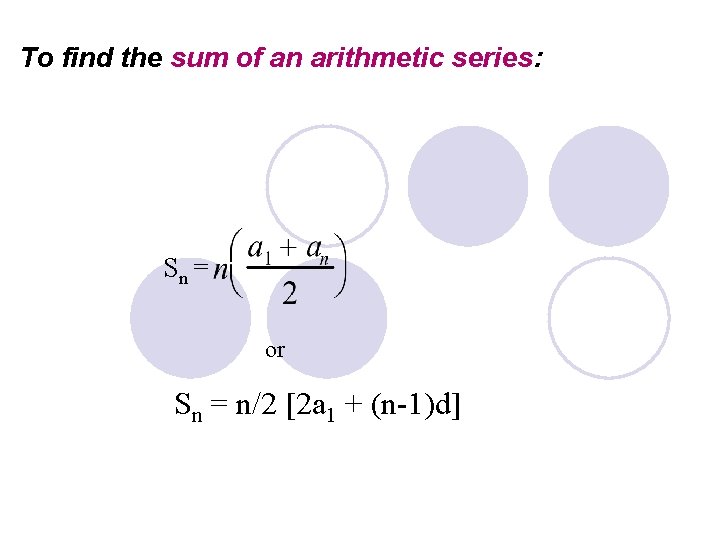
To find the sum of an arithmetic series: Sn = or Sn = n/2 [2 a 1 + (n-1)d]

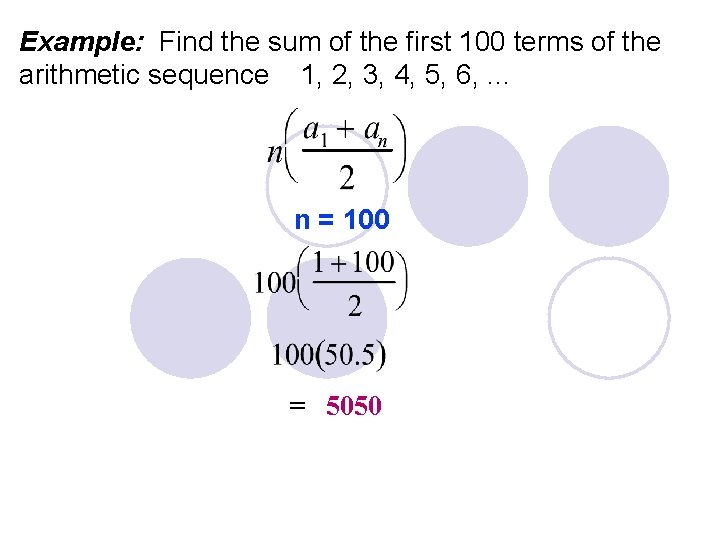
Example: Find the sum of the first 100 terms of the arithmetic sequence 1, 2, 3, 4, 5, 6, . . . n = 100 = 5050

Arithmetic means: l The arithmetic mean of two numbers a and b is defined as (a+b) / 2. This is the average of a & b. Insert 3 arithmetic means between 2 and 9. a 1 = 2 a 2 = ? a 3 = ? a 4 = ? a 5 = 9 an = a 1 + (n-1) d

l An explicit formula for a sequence shows how to calculate the value of each term from its subscript. l We can also specify a sequence by stating its starting value and a recursive formula that tells us how to calculate ak from one or more preceding values.

l k: 1 2 3 4 5 6 7 8 l ak: 7, 11, 15, 19, 23, 27, 31, 35. . . l Explicit formula ak = 7 + (k – 1) 4 = 4 k + 3 l Recursive formula ak = ak-1 + 4

10. 3 Geometric Sequences Plus a review of arithmetic sequences

Definitions l A sequence is a set of numbers, called terms, arranged in some particular order. l An arithmetic sequence is a sequence with the difference between two consecutive terms constant. The difference is called the common difference. l A geometric sequence is a sequence with a common ratio, r.

Examples: Find the common ratio of the following: 1) 1, 2, 4, 8, 16, . . . r = 2 2) 27, 9, 3, 1, 1/3, . . . r = 1/3 3) 3, 6, 12, 24, 48, . . . r = 2 4) 1/2, -1, 2, -4, 8, . . . r = -2

Examples: Find the next term in each of the previous sequences. 1) 1, 2, 4, 8, 16, . . . 32 2) 27, 9, 3, 1, 1/3, . . . 1/9 3) 3, 6, 12, 24, 48, . . . 96 4) 1/2, -1, 2, -4, 8, . . . -16

Let's play guess the sequence!: I give you a sequence and you guess the type. 1. 3, 8, 13, 18, 23, . . . 2. 1, 2, 4, 8, 16, . . . 3. 24, 12, 6, 3, 3/2, 3/4, . . . 4. 55, 51, 47, 43, 39, 35, . . . 5. 2, 5, 10, 17, . . . 6. 1, 4, 9, 16, 25, 36, . . .

Answers! 1) Arithmetic, the common difference d = 5 2) Geometric, the common ratio r = 2 3) Geometric, r = 1/2 4) Arithmetic, d = -4 5) Neither, why? (How about no common difference or ratio!) 6) Neither again! (This looks familiar, could it be from geometry? )

This is important! Arithmetic formula: an = a 1 + (n - 1)d an is the nth term, a 1 is the first term, and d is the common difference. Geometric formula: an = a 1. r (n - 1) an is the nth term, a 1 is the first term, and r is the common ratio.

Sample problems: Find the first four terms and state whether the sequence is arithmetic, geometric, or neither. 1) an = 3 n + 2 2) an = n 2 + 1 3) an = 3*2 n

Answers: 1) an = 3 n + 2 To find the first four terms, in a row, replace n with 1, then 2, then 3 and 4 Answer: 5, 8, 11, 14 The sequence is arithmetic! d = 3

2) an = n 2 + 1 To find the first four terms, do the same as above! Answer: 2, 5, 10, 17 The sequence is neither. Why?

3) an = 3*2 n Answer: 6, 12, 24, 48 The sequence is geometric with r = 2

Find a formula for each sequence. 1) 2, 5, 8, 11, 14, . . . It is arithmetic! an = 2 + (n - 1)3 and simplifying yields : an = 3 n -1

Find the indicated term of the sequence. 1) sequence is arithmetic with t 1 = 5 and t 7 = 29. Find t 53 29 = 5 + 6 d 24 = 6 d means d = 4 t 53 = 5 + 52. 4 = 213

How to find the sum of a finite Geometric Series Sn = a (1 - rn)/(1 - r) 1 To find the sum of a finite geometric series, you need to know three things: the first term, how many terms to add and the common ratio!!

Definition geometric series - the expression formed by adding the terms of a geometric sequence. Finding the Sum of the First n Terms of a Geometric Sequence. ¡ Use Sn = [a 1(1 - rn)/(1 - r)], Sn is the sum of the first n terms. ¡ Substitute the n, a, and r values into Sn = [a 1(1 - rn)/(1 - r)]. ¡ Simplify to find the sum.

Example: Find the sum of the first 10 terms of the geometric series 9 + 36 + 144 + 576 +. . . Answer: Sn = [a 1(1 - rn)/(1 - r)] Sn = [9(1 - 410)/(1 -4)] Sn = [9(-1048575)/(-3)] Sn = 3, 145, 725

Example: Find the sum of the first 10 terms of the geometric series 4 + 12 + 36 + 108 +. . . Answer: Sn = [a 1(1 - rn)/(1 - r)] Sn = [4(1 - 310)/(1 -3)] Sn = [4(-59, 048)/(-2)] Sn = 118, 096

Geometric Mean: l The geometric mean between two numbers is the square root of the product of the two numbers. l The geometric mean between 20 & 45 = √ 900 = 30

Finding the sum of an infinite geometric series If |r| < 1, then the infinite geometric series has the sum: Find the sum of the terms in the infinite geometric series 1/2+ 1/4+ 1/8 + 1/16 + … So, 1

10. 5 The Binomial Theorem

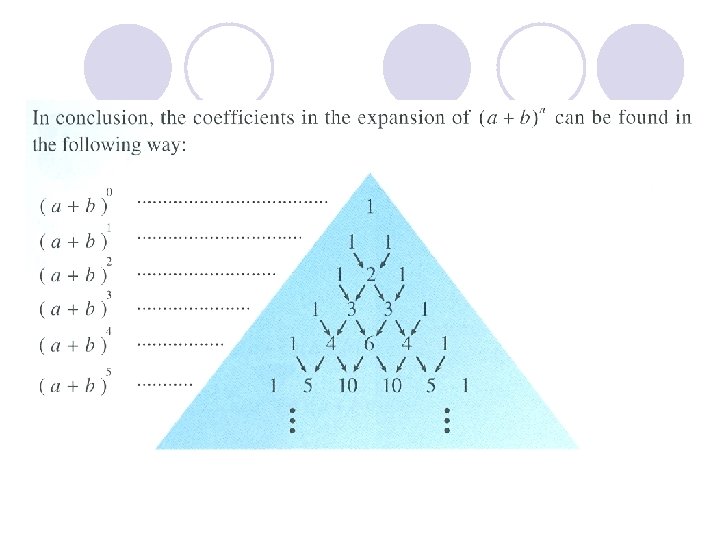
The Binomial Theorem (Binomial expansion) (a + b)1 = 1 a +1 b (a + b)2 = (a + b) coefficient =1 a 2 + 2 ab + 1 b 2 (a + b)3 = (a + b)(a + b) =1 a 3 + 3 a 2 b +3 ab 2 +1 b 3

The Binomial Theorem (Binomial expansion) (a + b)4 = (a + b)(a +b) =1 a 4 + 4 a 3 b +6 a 2 b 2 4 +4 ab 3+1 b Take out the coefficients of each expansion. 1

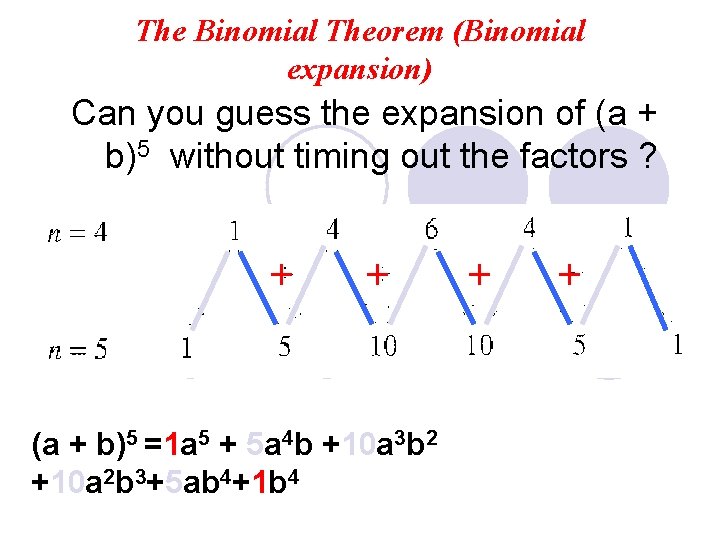
The Binomial Theorem (Binomial expansion) Can you guess the expansion of (a + b)5 without timing out the factors ? + + (a + b)5 =1 a 5 + 5 a 4 b +10 a 3 b 2 +10 a 2 b 3+5 ab 4+1 b 4 + +

The Binomial Theorem (Binomial expansion) Points to be noticed : l Coefficients are arranged in a Pascal triangle. l Summation of the indices of each term is equal to the power (order) of the expansion. l The first term of the expansion is arranged in descending order after the expansion. l The second term of the expansion is arranged in ascending order after the expansion. l Number of terms in the expansion is equal to the power of the expansion plus one.

The Notation of Factorial and Combination Factorial ---- the product of the first n positive integers i. e. n！ = n(n-1)(n-2)(n-3)…. 0！is defined to be 1. i. e. 0！= 1

10. 6 Permutations

Fundamental counting principle: m 1*m 2*m 3*…mk l At a restaurant, one can choose from 6 salads, 3 meats, 4 vegetables, and 2 desserts. How many different salad-meatvegetable-dessert combinations? 6*3*4*2 = 144

Permutations l A permutation is an ordered arrangement of the elements of some set S ¡ Let S = {a, b, c} ¡ c, b, a is a permutation of S ¡ b, c, a is a different permutation of S l An r-permutation is an ordered arrangement of r elements of the set ¡ A♦, 5♥, 7♣, 10♠, K♠ is a 5 -permutation of the set of cards l The notation for the number of r-permutations: P(n, r) ¡ The poker hand is one of P(52, 5) permutations

Permutations l Number of poker hands (5 cards): ¡ P(52, 5) = 52*51*50*49*48 = 311, 875, 200 l Number of (initial) blackjack hands (2 cards): ¡ P(52, 2) = 52*51 = 2, 652 l r-permutation notation: P(n, r) ¡ The poker hand is one of P(52, 5) permutations

r-permutations example l How many ways are there for 5 people in this class to give presentations? l There are 27 students in the class ¡P(27, 5) = 27*26*25*24*23 = 9, 687, 600 ¡Note that the order they go in does matter in this example!

Permutation formula proof l There are n ways to choose the first element ¡n-1 ways to choose the second ¡n-2 ways to choose third ¡… ¡n-r+1 ways to choose the rth element l By the product rule, that gives us: P(n, r) = n(n-1)(n-2)…(n-r+1)

Permutations vs. r-permutations l r-permutations: Choosing an ordered 5 card hand is P(52, 5) ¡When people say “permutations”, they almost always mean r-permutations l. But the name can refer to both l Permutations: Choosing an order for all 52 cards is P(52, 52) = 52! ¡Thus, P(n, n) = n!

l How many permutations of {a, b, c, d, e, f, g} end with a? ¡Note that the set has 7 elements l The last character must be a ¡The rest can be in any order l Thus, we want a 6 -permutation on the set {b, c, d, e, f, g} l P(6, 6) = 6! = 720

l How many ways are there to sit 6 people around a circular table, where seatings are considered to be the same if they can be obtained from each other by rotating the table? l First, place the first person in the north-most chair ¡ Only one possibility l Then place the other 5 people ¡ There are P(5, 5) = 5! = 120 ways to do that l By the product rule, we get 1*120 =120 l l Alternative means to answer this: There are P(6, 6)=720 ways to seat the 6 people around the table For each seating, there are 6 “rotations” of the seating Thus, the final answer is 720/6 = 120

l A baseball team consists of nine players. Find the number of ways of arranging the first four positions in the batting order if the pitcher is excluded. P(8, 4) = 1680

l If 8 basketball teams are in a tournament, find the number of different ways that first, second, & third place can be decided, assuming ties are not allowed. P(8, 3) = 336

10. 7 Distinguished Permutations & Combinations

Permutations vs. Combinations l Both are ways to count the possibilities l The difference between them is whether order matters or not l Consider a poker hand: ¡ A♦, 5♥, 7♣, 10♠, K♠ l Is that the same hand as: ¡ K♠, 10♠, 7♣, 5♥, A♦ l Does the order the cards are handed out matter? ¡ If yes, then we are dealing with permutations ¡ If no, then we are dealing with combinations

Combinations l What if order doesn’t matter? l In poker, the following two hands are equivalent: ¡ A♦, 5♥, 7♣, 10♠, K♠ ¡ K♠, 10♠, 7♣, 5♥, A♦ l The number of r-combinations of a set with n elements, where n is non-negative and 0≤r≤n is:

Distinguishable Permutations: l Of two arrangements of objects, one arrangement cannot be obtained from the other by rearranging like objects. l Thus, BBBWR & BRBWB are distinguishable permutations. l If, in a collection of n objects, n are alike of one kind, n 2 are alike of another kind, …, nk are alike of a further kind, the # of distinguishable permutations is

l Find the number of distinguishable permutations of the letters in the word MISSISSIPPI.

Combinations example l How many different poker hands are there (5 cards)? l How many different (initial) blackjack hands are there?

Example l A little league baseball squad has six outfielders, seven infielders, five pitchers, and two catchers. Each outfielder can play any of the three outfield positions, and each infielder can play any of the four infield positions. In how many ways can a team of nine players be chosen?

A last note on combinations l An alternative (and more common) way to denote an r-combination: l I’ll use C(n, r) whenever possible, as it is easier to write in Power. Point

10. 8 Probability l Objective: Students will be introduced to both theoretical and experimental probabilities. Students will also find probabilities of mutually exclusive events.

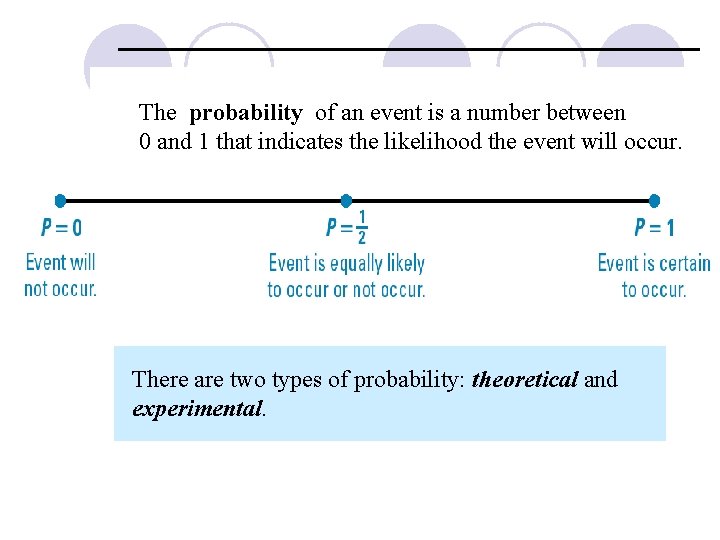
The probability of an event is a number between 0 and 1 that indicates the likelihood the event will occur. There are two types of probability: theoretical and experimental.

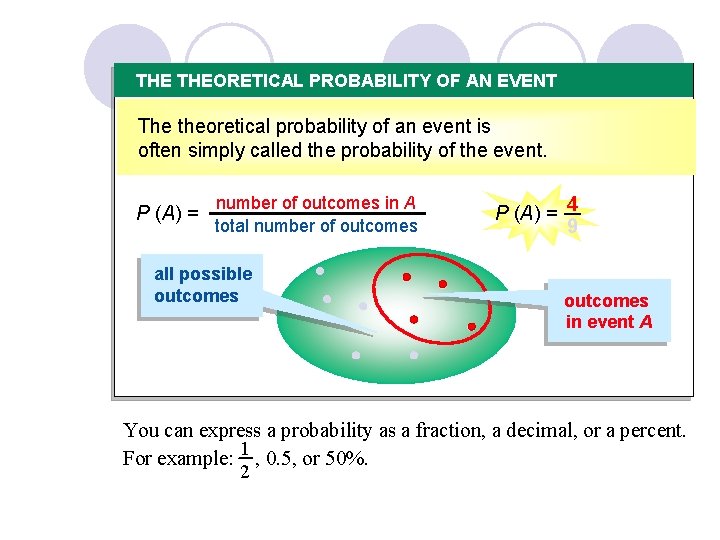
THE THEORETICAL PROBABILITY OF AN EVENT The theoretical probability of an event is When all outcomes are equally likely, the often simply called the probability of the event. theoretical probability that an event A will occur is: P (A) = number of outcomes in A total number of outcomes all possible outcomes P (A) = 4 9 outcomes in event A You can express a probability as a fraction, a decimal, or a percent. For example: 1 , 0. 5, or 50%. 2

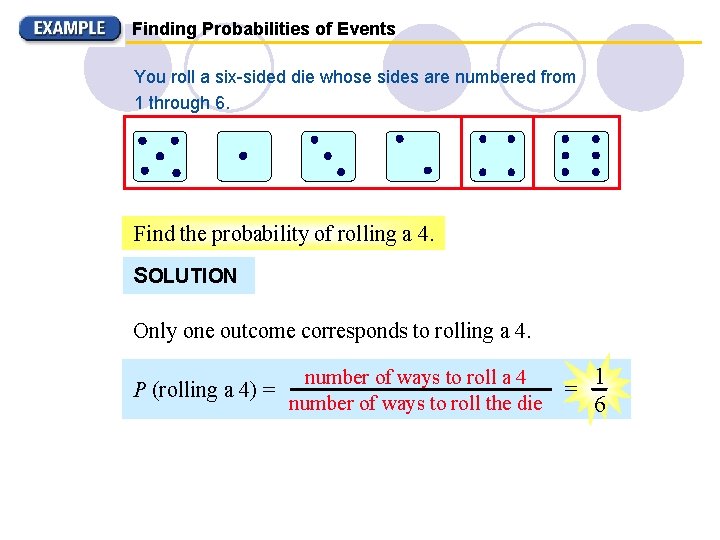
Finding Probabilities of Events You roll a six-sided die whose sides are numbered from 1 through 6. Find the probability of rolling a 4. SOLUTION Only one outcome corresponds to rolling a 4. number of ways to roll a 4 P (rolling a 4) = number of ways to roll the die 1 = 6

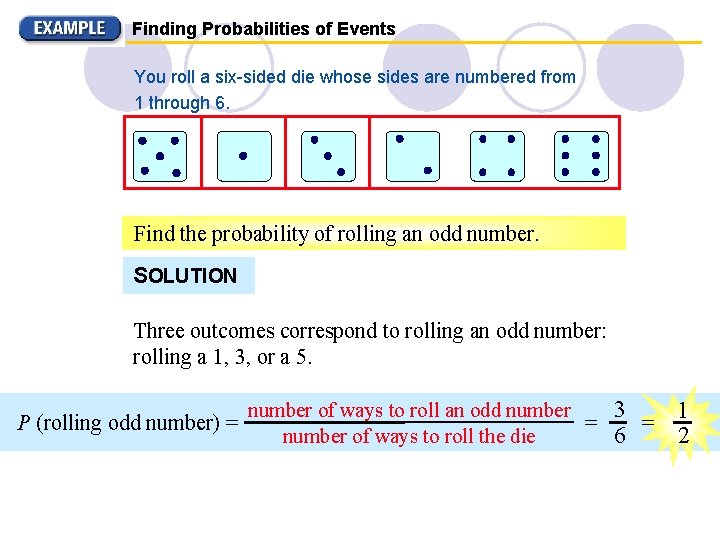
Finding Probabilities of Events You roll a six-sided die whose sides are numbered from 1 through 6. Find the probability of rolling an odd number. SOLUTION Three outcomes correspond to rolling an odd number: rolling a 1, 3, or a 5. P (rolling odd number) = number of ways to roll an odd number 3 = = number of ways to roll the die 6 1 2

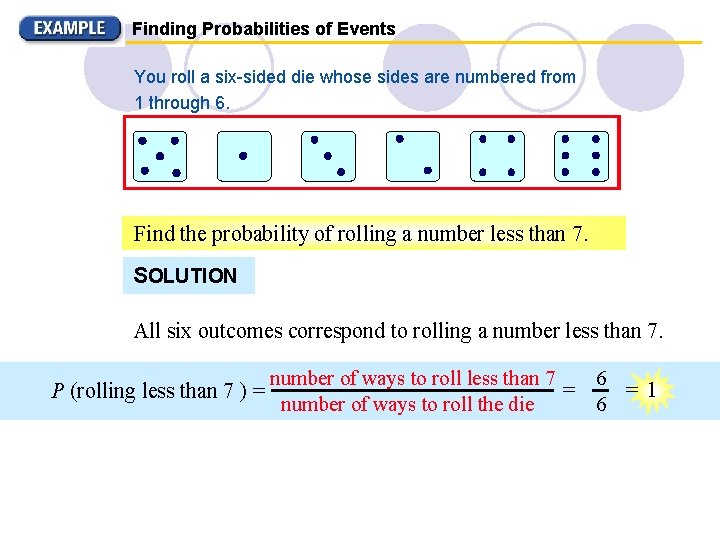
Finding Probabilities of Events You roll a six-sided die whose sides are numbered from 1 through 6. Find the probability of rolling a number less than 7. SOLUTION All six outcomes correspond to rolling a number less than 7. P (rolling less than 7 ) = number of ways to roll less than 7 6 = =1 number of ways to roll the die 6

Probabilities Involving Permutations or Combinations You put a CD that has 8 songs in your CD player. You set the player to play the songs at random. The player plays all 8 songs without repeating any song. What is the probability that the songs are played in the same order they are listed on the CD? SOLUTION There are 8! different permutations of the 8 songs. Of these, only 1 is the order in which the songs are listed on the CD. So, the probability is: P(playing 8 in order) = 1 1 = 0. 0000248 8! 40, 320 Help

Probabilities Involving Permutations or Combinations You put a CD that has 8 songs in your CD player. You set the player to play the songs at random. The player plays all 8 songs without repeating any song. You have 4 favorite songs on the CD. What is the probability that 2 of your favorite songs are played first, in any order? Help SOLUTION There are 8 C 2 different combinations of 2 songs. Of these, 4 C 2 contain 2 of your favorite songs. So, the probability is: P(playing 2 favorites first) = 4 C 2= 8 C 2 3 6 = 0. 214 14 28

Probabilities Involving Permutations or Combinations Sometimes it is not possible or convenient to find theoretical probability of an event. In such cases you may be able to calculate an experimental probability by performing an experiment, conducting a survey, or looking at the history of the event.

Finding Experimental Probabilities In 1998 a survey asked Internet users for their ages. The results are shown in the bar graph.

Finding Experimental Probabilities Find the experimental probability that a randomly selected Internet user is at most 20 years old. 1636 6617 3693 491 6 SOLUTION The number of people surveyed was 1636 + 6617 + 3693 + 491 + 6 = 12, 443. Of the people surveyed, 16 36 are at most 20 years old. So, the probability is: P(user is at most 20) = 1636 0. 131 12, 443

Finding Experimental Probabilities Find the experimental probability that a randomly selected Internet user is at least 41 years old. Given that 12, 443 people were surveyed. SOLUTION Of the people surveyed, 3693 + 491 + 6 = 4190 are at least 41 years old. So, the probability is: P(user is at least 41) = 4190 0. 337 12, 443

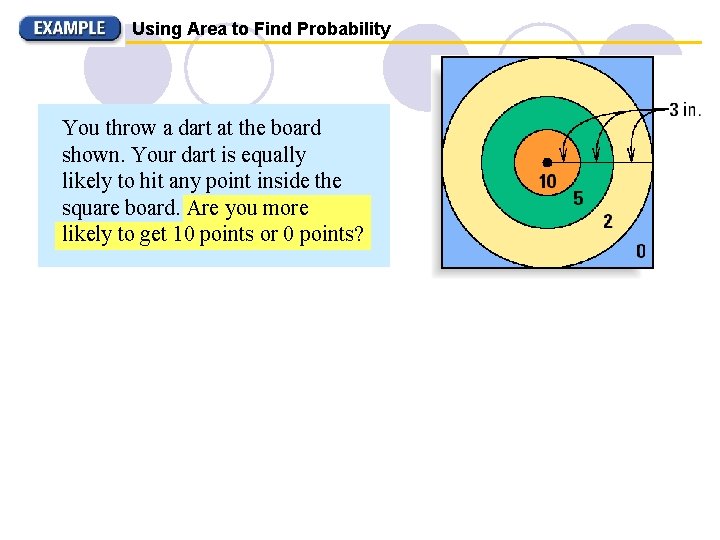
Using Area to Find Probability You throw a dart at the board shown. Your dart is equally likely to hit any point inside the square board. Are you more likely to get 10 points or 0 points?

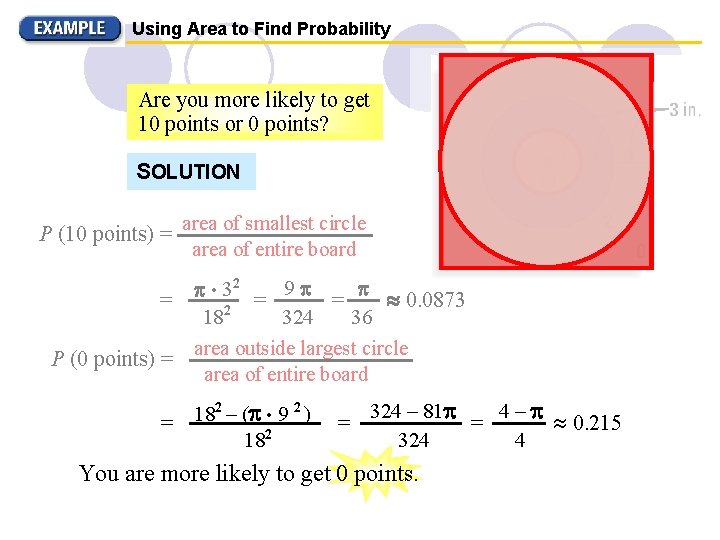
Using Area to Find Probability Are you more likely to get 10 points or 0 points? SOLUTION P (10 points) = area of smallest circle area of entire board 9 • 32 = = = 0. 0873 2 18 324 36 area outside largest circle P (0 points) = area of entire board 2 18 – ( • 9 2) = 182 = 324 – 81 4– = 0. 215 324 4 You are more likely to get 0 points.

10. 8 (day 2) Probability of Compound Events P. 724

Mutually Exclusive Events

Intersection of A & B

l To find P(A or B) you must consider what outcomes, if any, are in the intersection of A and B. l If there are none, then A and B are mutually exclusive events and P(A or B) = P(A)+P(B) l If A and B are not mutually exclusive, then the outcomes in the intersection or A & B are counted twice when P(A) & P(B) are added. l So P(A & B) must be subtracted once from

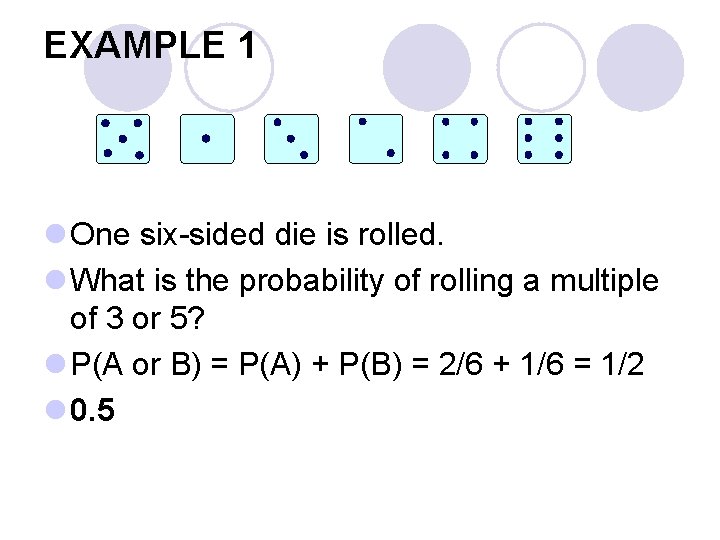
EXAMPLE 1 l One six-sided die is rolled. l What is the probability of rolling a multiple of 3 or 5? l P(A or B) = P(A) + P(B) = 2/6 + 1/6 = 1/2 l 0. 5

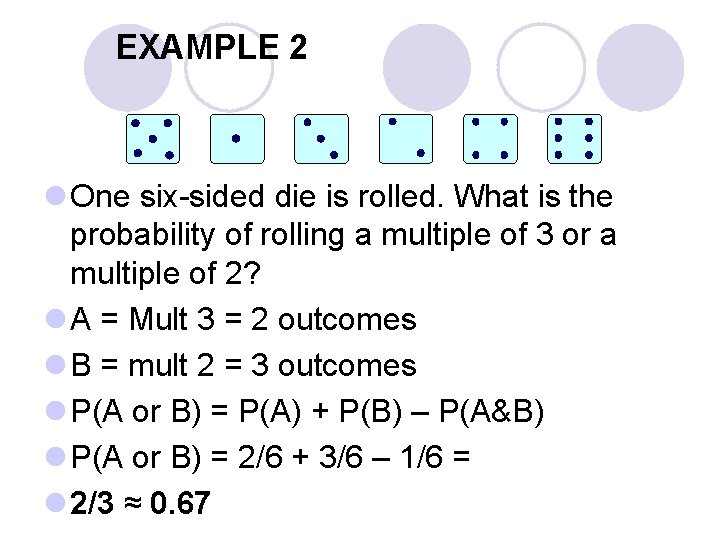
EXAMPLE 2 l One six-sided die is rolled. What is the probability of rolling a multiple of 3 or a multiple of 2? l A = Mult 3 = 2 outcomes l B = mult 2 = 3 outcomes l P(A or B) = P(A) + P(B) – P(A&B) l P(A or B) = 2/6 + 3/6 – 1/6 = l 2/3 ≈ 0. 67

EXAMPLE 3 l In a poll of high school juniors, 6 out of 15 took a French class and 11 out of 15 took a math class. l Fourteen out of 15 students took French or math. l What is the probability that a student took both French and math?

l A = French l B = Math l P(A) = 6/15, P(B) = 11/15, P(Aor. B) = 14/15 l P(A or B) = P(A) + P(B) – P(A&B) l 14/15 = 6/15 + 11/15 – P(A & B) l P(A & B) = 6/15 + 11/15 – 14/15 l P(A & B) = 3/15 = 1/5 =. 20

Using complements to find Probability l The event A’, called the complement of event A, consists of all outcomes that are not in A. l The notation A’ is read ‘A prime’.

Probability of the complement of an event l. The probability of the complement of A is : l. P(A’) = 1 - P(A)

EXAMPLE 4 l. A card is randomly selected from a standard deck of 52 cards. l. Find the probability of the given event. la. The card is not a king. ¡P(K) = 4/52 so P(K’) = l 48/52 ≈ 0. 923

l b. The card is not an ace or a jack. l P(not ace or Jack) = 1 -(P(4/52 + 4/52)) l = 1 - 8/52 l = 44/52 ≈ 0. 846

Probability of Independent and Dependent Events

l. Two events are Independent if the occurrence of 1 has no effect on the occurrence of the other. (a coin toss 2 times, the first toss has no nd effect on the 2 toss)

Probability of Two Independent Events (can be extended to probability of 3 or more ind. events) l A & B are independent events then the probability that both A & B occur is: l. P(A and B) = P(A) • P(B)

BASEBALL l During the 1997 baseball season, the Florida Marlins won 5 out of 7 home games and 3 out of 7 away games against the San Francisco Giants. During the 1997 National League Division Series with the Giants, the Marlins played the first two games at home and the third game away. The Marlins won all three games. l Estimate the probability of this happening. _ Source: The Florida Marlins

l. Let A, B, & C be winning the 1 st, 2 nd, & 3 rd games l The three events are independent and have experimental probabilities based on the regular season games. l. P(A&B&C) = P(A)*P(B)*P(C) = l 5/7 * 3/7 = 75/343 l=. 219

PROBABILITIES OF DEPENDENT EVENTS l Two events A and B are dependent events if the occurrence of one affects the occurrence of the other. l The probability that B will occur given that A has occurred is called the conditional probability of B given A and is written P(B|A).

Probability of Dependent Events l. If A & B are dependant events, then the probability that both A & B occur is: l. P(A&B) = P(A) * P(B/A)

Comparing Dependent and Independent Events l You randomly select two cards from a standard 52 -card deck. What is the probability that the first card is not a face card (a king, queen, or jack) and the second card is a face card if l (a) you replace the first card before selecting the second, and l (b) you do not replace the first card?

l (A) If you replace the first card before selecting the second card, then A and B are independent events. So, the probability is: l P(A and B) = P(A) • P(B) = 40 * 12 = 30 52 169 l ≈ 0. 178 l (B) If you do not replace the first card before selecting the second card, then A and B are dependent events. So, the probability is: l P(A and B) = P(A) • P(B|A) = 40*12 = 40 52 51 221 l ≈ 0. 181

l http: //www. youtube. com/watch? v=Xll. Kz 2 c X 73 Q