10 1 DEFINITION OF A SEQUENCE An infinite

10. 1 DEFINITION OF A SEQUENCE An infinite sequence is a function whose domain is the set of positive integers. The function values are called the terms of the sequence. The nth term, an, is called the general term of the sequence. a 1, a 2, a 3, a 4, … , an, …, © 2010 Pearson Education, Inc. All rights reserved 1

Finding a General Term of a Sequence from a Pattern v Write the general term an for a sequence whose first five terms are given. v To do this, write the position number of the term above each term of the sequence and look for a pattern that connects the term to the position number of the term. Apparent pattern: Here 1 = 12, 4 = 22, 9 = 32, 16 = 42, and 25 =52. Each term is the square of the position number of that term. This suggests an = n 2. Apparent pattern: When the terms alternate in sign and n = 1, use factors such as (− 1)n if we want to begin with the factor − 1 or we use factors such as (− 1)n+1 to begin with the factor 1. © 2010 Pearson Education, Inc. All rights reserved 2

RECURSIVE FORMULAS A recursive formula requires that one or more of the first few terms of the sequence be specified and all other terms be defined in relation to previously defined terms. The Fibonacci sequence is a famous sequence that is defined recursively and shows up often in nature. In this sequence, we specify the first two terms as a 0 = 1 and a 1 = 1; each subsequent term is the sum of the two terms immediately preceding it. 1 1 2 3 5 8…ak , where ak-2 + ak-1 v Write the first five terms of the recursively defined sequence a 1 = 4, an+1 = 2 an – 9 We are given the first term of the sequence: a 1 = 4. a 2 = 2 a 1 – 9 = 2(4) – 9 = – 1 a 3 = 2 a 2 – 9 = 2(– 1) – 9 = – 11 a 4 = 2 a 3 – 9 = 2(– 11) – 9 = – 31 a 5 = 2 a 4 – 9 = 2(– 31) – 9 = – 71 So the first five terms of the sequence are: 4, – 1, − 11, − 31, − 71 © 2010 Pearson Education, Inc. All rights reserved 3

DEFINITION OF FACTORIAL For any positive integer n, n factorial (written n!) is defined as and = 16 · 15 = 240 = (n + 1) n © 2010 Pearson Education, Inc. All rights reserved 4

SUMMATION NOTATION The sum of the first n terms of a sequence a 1, a 2, a 3, …, an, … is The letter i in the summation notation is called the index of summation, n is called the upper limit, and 1 is called the lower limit, of the summation. © 2010 Pearson Education, Inc. All rights reserved 5

SUMMATION PROPERTIES © 2010 Pearson Education, Inc. All rights reserved 6

DEFINITION OF A SERIES Let a 1, a 2, a 3, … , ak, … be an infinite sequence. Then 1. The sum of the first n terms of the sequence is called the nth partial sum of the sequence and is denoted by (This sum is a finite series. ) 2. The sum of all terms of the infinite sequence is called an infinite series and is denoted by © 2010 Pearson Education, Inc. All rights reserved 7

Writing a Partial Sum in Summation Notation Write each sum in summation notation. a. This is the sum of consecutive odd integers from 3 to 21. Each can be expressed as 2 k + 1, starting with k = 1 and ending with k = 10. b. This finite series is the sum of fractions, each of which has numerator 1 and denominator k 2, starting with k = 2 and ending with k = 7. © 2010 Pearson Education, Inc. All rights reserved 8

10. 2 DEFINITION OF AN ARITHMETIC SEQUENCE The sequence a 1, a 2, a 3, a 4, … , an, … is an arithmetic sequence, or an arithmetic progression if there is a number d such that each term in the sequence except the first is obtained from the preceding term by adding d to it. The number d is called the common difference of the arithmetic sequence. We have d = an + 1 – an, n ≥ 1. An arithmetic sequence a 1, a 2, a 3, a 4, … , an, … can be defined recursively. The recursive formula an + 1 = an + d for n ≥ 1 defines an arithmetic sequence with first term a 1 and common difference d. If a sequence a 1, a 2, a 3, … is an arithmetic sequence, then its nth term, an, is given by an = a 1 + (n – 1)d where a 1 is the first term and d is the common difference. © 2010 Pearson Education, Inc. All rights reserved 9

Common Difference of an Arithmetic Sequence Example: Find the common difference d and the nth term an of an arithmetic sequence whose 5 th term is 15 and whose 20 th term is 45. Solving the system of equations gives a 1 = 7 and d = 2. The nth term is given by an = 2 n + 5, n ≥ 1. © 2010 Pearson Education, Inc. All rights reserved 10

SUM OF n TERMS OF AN ARITHMETIC SEQUENCE Let a 1, a 2, a 3, … an be the first n terms of an arithmetic sequence with common difference d. The sum Sn of these n terms is given by where an = a 1 + (n – 1)d. Example: Find the sum of the arithmetic sequence of numbers: 1 + 4 + 7 + … + 25 Arithmetic sequence with a 1 = 1 and d = 3. First find the number of terms. Thus 1 + 4 + 7 + … + 25 = 117. © 2010 Pearson Education, Inc. All rights reserved 11

10. 3 DEFINITION OF A GEOMETRIC SEQUENCE The sequence a 1, a 2, a 3, a 4, … , an, …is a geometric sequence, or a geometric progression, if there is a number r such that each term except the first in the sequence is obtained by multiplying the previous term by r. The number r is called the common ratio of the geometric sequence. Thus, an + 1 = ran, n ≥ 1 Every geometric sequence can be written in the form a 1, a 1 r 2, a 1 r 3, … , a 1 rn− 1, … Since a 1 = a 1(1) = a 1 r 0, the nth term of the geometric sequence is an = a 1 rn– 1, for n ≥ 1. Example 1: Geometric sequence 1, 3, 9, 27, … Find a 1, r, and an a 1 = 1 (1 st term) r = 9/3 (ratio of consecutive terms) = 3 An = a 1 rn-1 = (1)(3 n-1)=3 n-1 © 2010 Pearson Education, Inc. All rights reserved Example 2: Find the 23 rd term of a geometric sequence with first term 10 & common ratio 1. 2 An = a 1 rn-1 = (10)(1. 2)23 -1 = 552. 06 12

SUM OF THE TERMS OF A FINITE GEOMETRIC SEQUENCE Let a 1, a 2, a 3, … an be the first n terms of a geometric sequence with first term a 1 and common ration r. The sum Sn of these terms is Examples: Find the sum of a. A 1 = 5, r =. 7, n = 15 © 2010 Pearson Education, Inc. All rights reserved 13

SUM OF THE TERMS OF AN INFINITE GEOMETRIC SEQUENCE If |r| < 1, the infinite sum a 1 + a 1 r 2 + a 1 r 3 + … + a 1 rn– 1 + … is Example: Find the sum © 2010 Pearson Education, Inc. All rights reserved 14

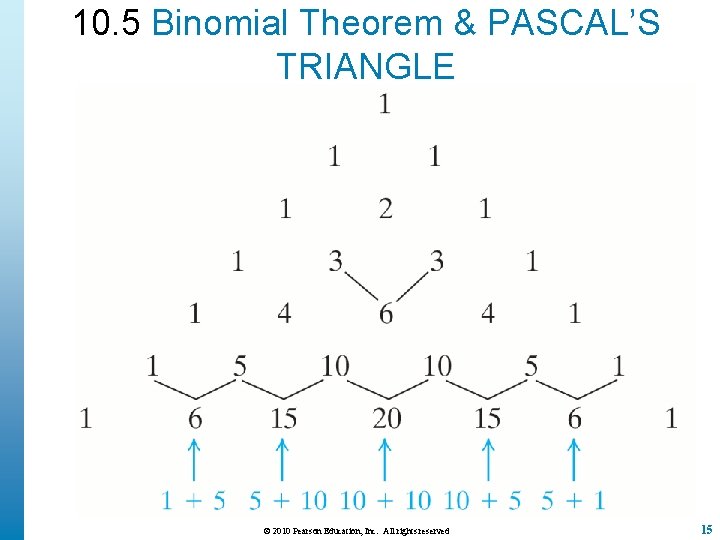
10. 5 Binomial Theorem & PASCAL’S TRIANGLE © 2010 Pearson Education, Inc. All rights reserved 15

BINOMIAL EXPANSIONS The patterns for expansions of (x+ y)n (with n = 1, 2, 3, 4, 5) suggest: 1. The expansion of (x+ y)n has n + 1 terms. 2. The sum of the exponents on x and y in each term equals n. 3. The exponent on x starts at n (xn = xn · y 0) in the first term and decreases by 1 for each term until it is 0 in the last term (x 0 · yn = yn). 4. The exponent on y starts at 0 in the first term (xn = xn · y 0) and increases by 1 for each term until it is n in the last term (x 0 · yn = yn). 5. The variables x and y have symmetrical roles. That is, replacing x with y and y with x in the expansion of (x+ y)n yields the same terms, just in a different order. • • • Coefficients of 1 st & last terms are both 1 Coefficients of the second and the next-to-last terms are equal. In general the coefficients of xn−jyj and xjyn−j are equal for j = 0, 1, 2, …, n. Coefficients in binomial expansion of (x + y)n are the binomial coefficients. Coefficients of each term of (x + y)n can be determined using Pascal’s Triangle. Top row represents coefficients of (x + y)0, Next row (x + y)1, etc. © 2010 Pearson Education, Inc. All rights reserved 16

Using Pascal’s Triangle to Expand a Binomial Power Example: Expand (4 y – 2 x)5. The fifth row of Pascal’s Triangle yields coefficients 1, 5, 10, 5, 1. Replace x with 4 y and y with – 2 x. © 2010 Pearson Education, Inc. All rights reserved 17

Evaluating Binomial Coefficients/Combinations = Ti 83/84 5 C = 5 [Math][PRB][n. Cr][Enter] 3 18 3

THE BINOMIAL THEOREM If n is a natural number, then the binomial expansion of (x + y)n is given by Example: Find the binomial expansion of (x – 3 y)4 = [x + (– 3 y)]4 4 © 2010 Pearson Education, Inc. All rights reserved 19

PARTICULAR TERM IN A BINOMIAL EXPRESSION The term containing the factor xr in the expansion of (x + y)n is Example: Find the term containing x 10 in the expansion of (x + 2 a)15. © 2010 Pearson Education, Inc. All rights reserved 20

10. 4 Using Mathematical Induction Use mathematical induction to prove that, for all natural numbers n, First: Verify that the statement is true for n = 1. Second: Assume the formula is true for k 2 + 4 + 6 + … + 2 k = k(k + 1) Third: On the basis the formula is true for k, show it is true for k+1, which means start from the second step above and show the following statement is true. 2 + 4 + 6 + … + 2(k+1) = (k + 1)(k + 1) 2 + 4 + 6 + … + 2 k + 2(k+1) = k(k+1) + 2(k+1) 2 + 4 + 6 + … + 2 k + 2(k+1) = (k + 1)(k + 2) 2 + 4 + 6 + … + 2 k + 2(k+1) = (k + 1)(k + 1) Thus, by induction, the formula is true for all natural numbers, n. © 2010 Pearson Education, Inc. All rights reserved 21

Mathematical Induction Continued… Use mathematical induction to prove for all natural numbers that First: Verify that the statement is true for n = 1. Second: Assume the formula is true for k 2 k > k Third: On the basis the formula is true for k, show it is true for k+1, which means start from the second step above and show the following statement is true. 2 k+1 > k+1 [Note: 2 k+1 > (2 k)(21) ] 2 k ∙ 21 > k ∙ 21 2 k ∙ 2 > 2 k 2 k = k + k ≥ k + 1 Thus, by induction, 2 k+1 > k + 1 is true so 2 n+1 > n for all natural numbers, n. © 2010 Pearson Education, Inc. All rights reserved 22