n 0 1 2 3 4 5 6
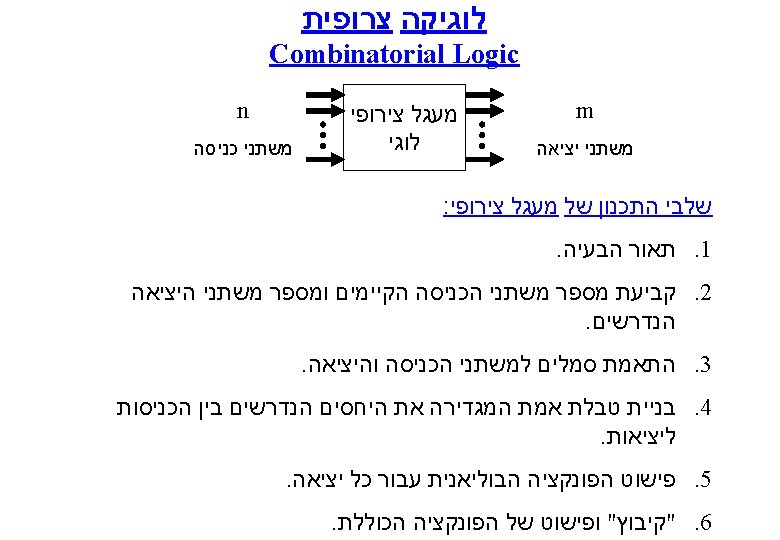


- Slides: 28



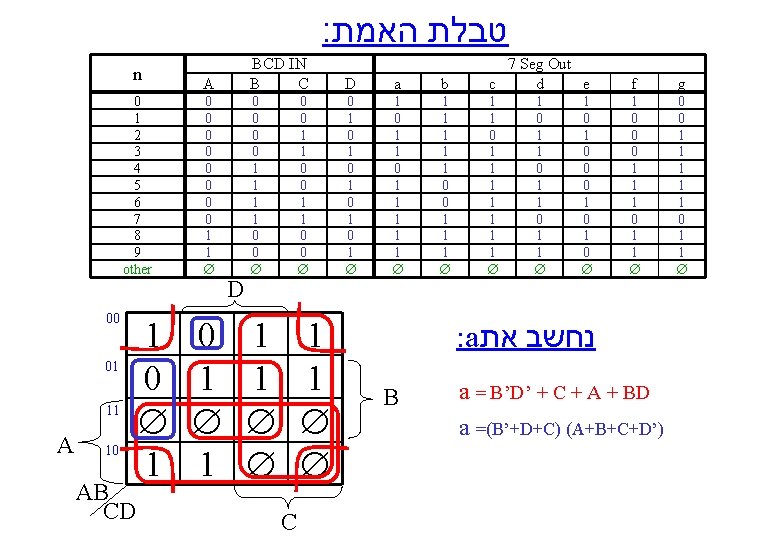
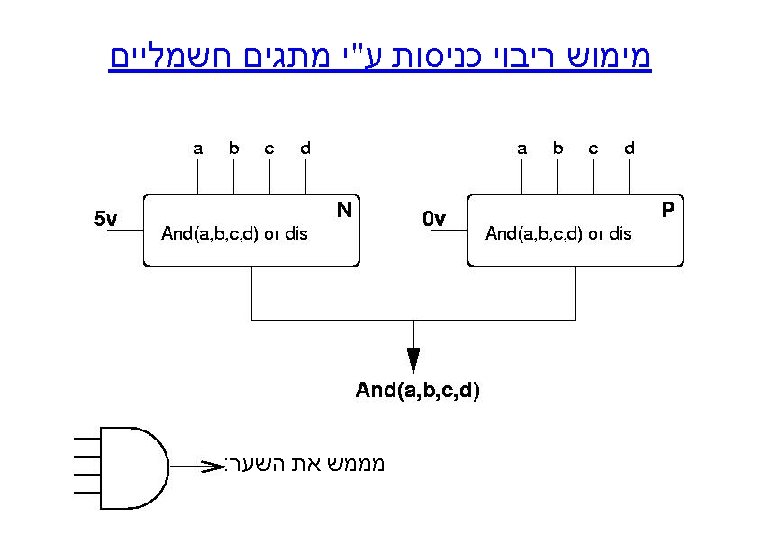
: טבלת האמת n 0 1 2 3 4 5 6 7 8 9 other 00 01 11 A 10 AB CD 1 0 1 A BCD IN B C D a 0 0 0 0 1 1 0 0 1 1 0 0 0 1 0 1 0 1 1 1 1 1 0 1 1 D C b 7 Seg Out c d e f g 1 1 1 0 0 1 1 1 1 1 0 0 0 1 1 1 0 1 1 0 1 1 1 0 0 0 1 0 : a נחשב את B a = B’D’ + C + A + BD a =(B’+D+C) (A+B+C+D’)

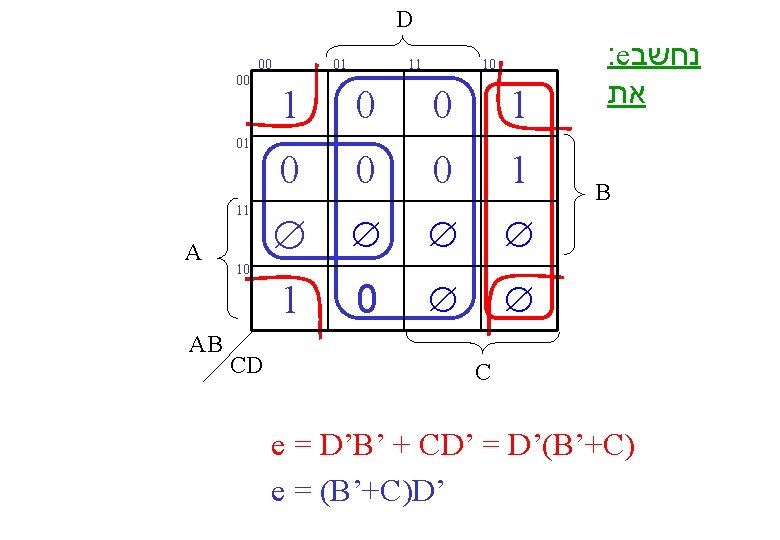
D 00 00 01 11 A AB 01 10 1 0 0 0 1 1 0 10 CD 11 : e נחשב את B C e = D’B’ + CD’ = D’(B’+C) e = (B’+C)D’


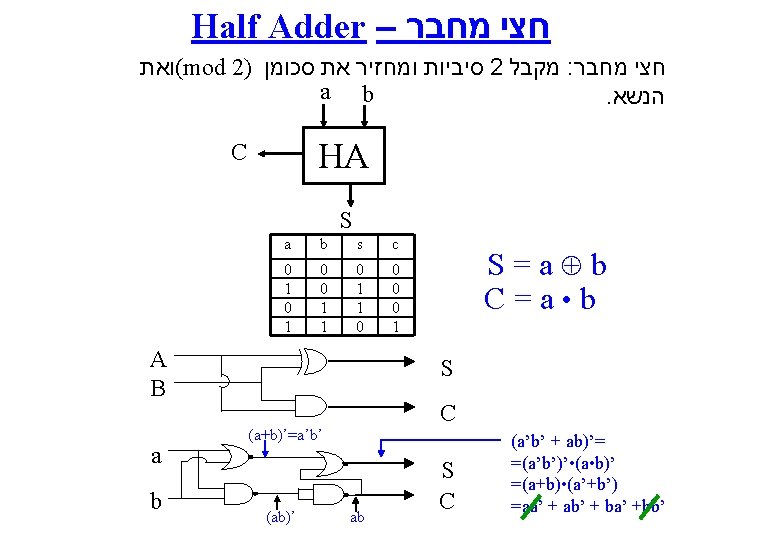
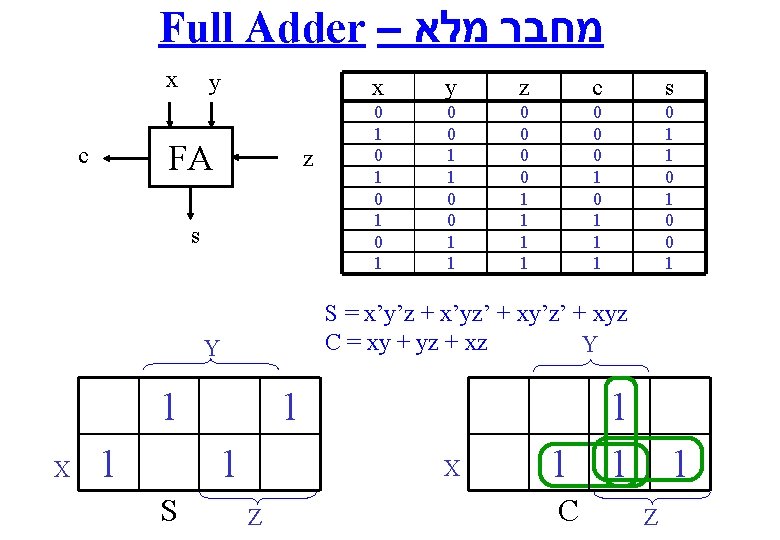
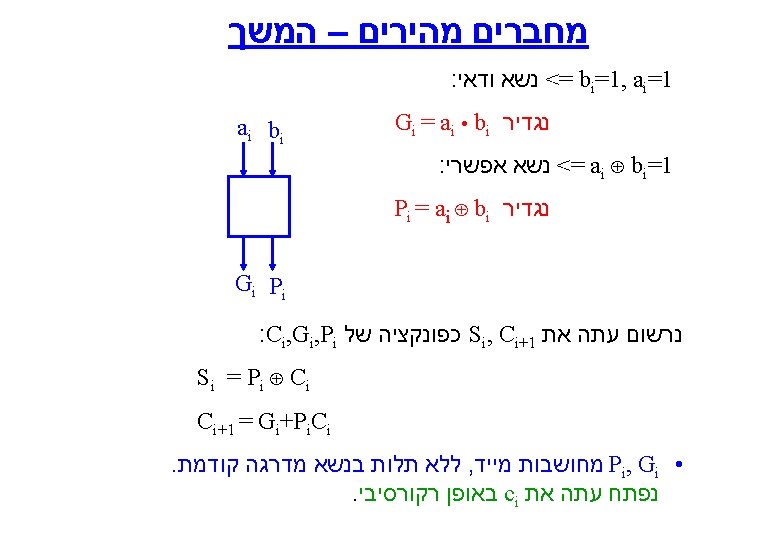
Full Adder – מחבר מלא x y FA c z s 1 1 z c s 0 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 0 0 1 1 1 S y S = x’y’z + x’yz’ + xy’z’ + xyz C = xy + yz + xz Y Y X x X Z 1 C 1 1 1 Z

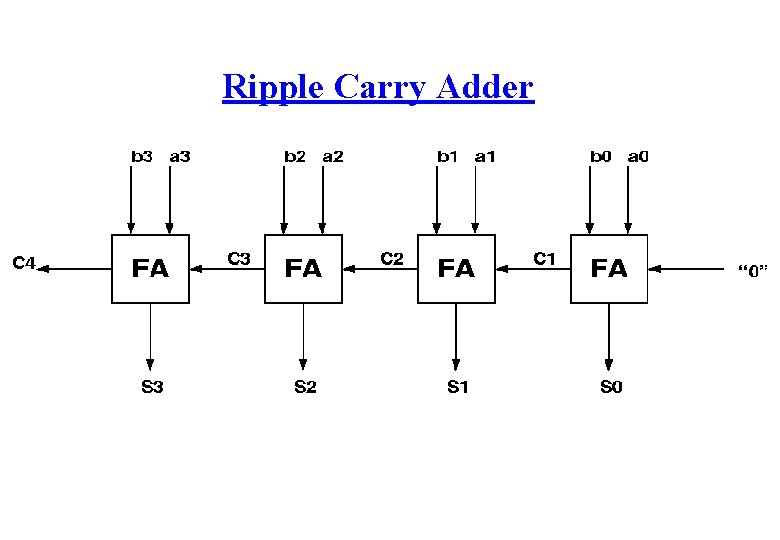
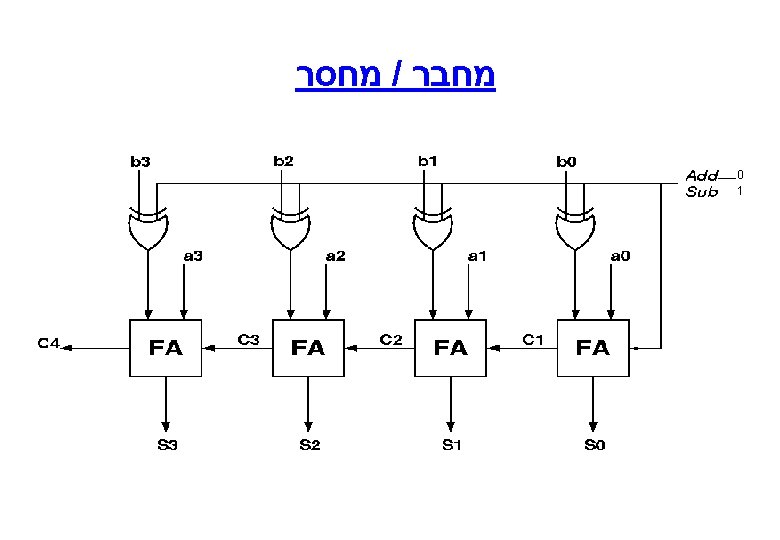
Ripple Carry Adder

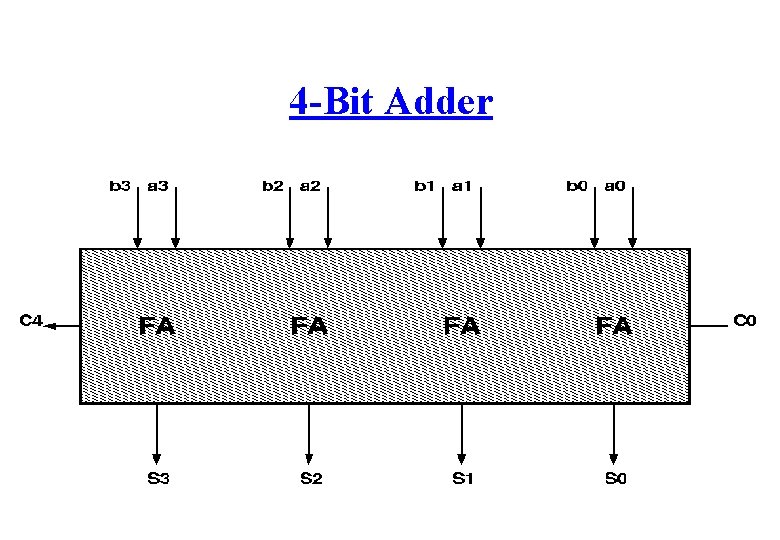
4 -Bit Adder


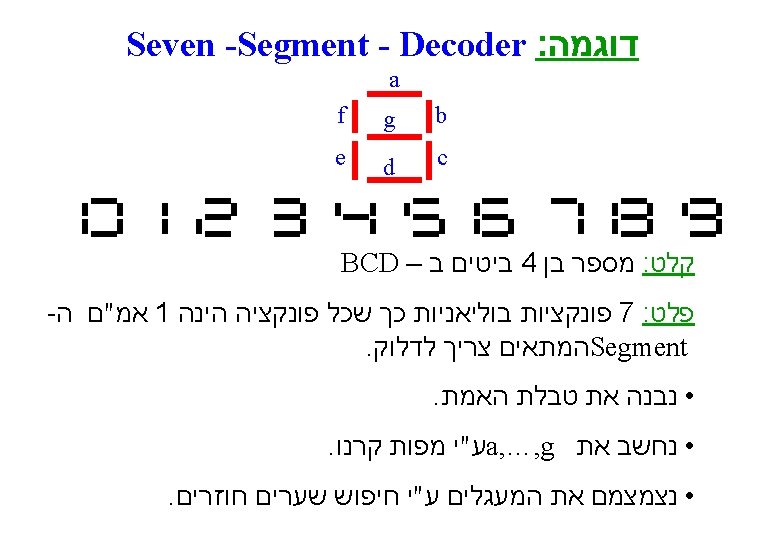
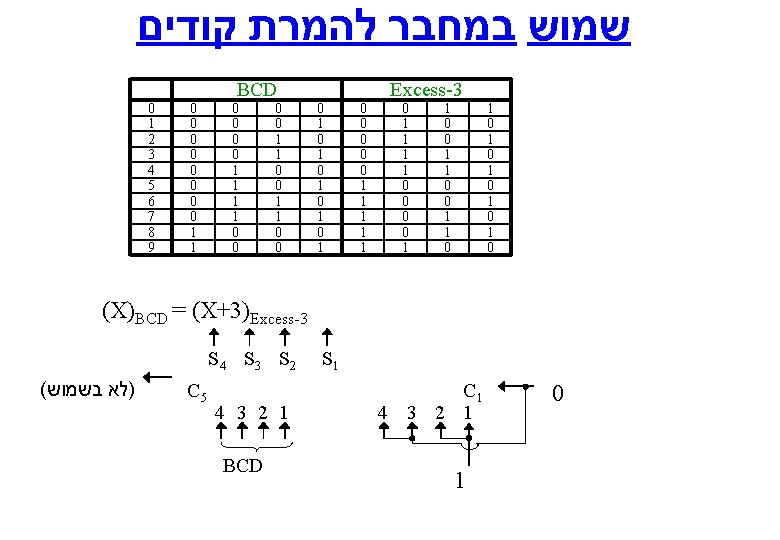
שמוש במחבר להמרת קודים 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 1 BCD 0 0 1 1 0 0 0 1 0 1 0 1 0 0 0 1 1 1 Excess-3 0 1 1 0 0 1 1 0 1 0 1 0 (X)BCD = (X+3)Excess-3 S 4 S 3 S 2 ( )לא בשמוש C 5 4 3 2 1 BCD S 1 C 1 4 3 2 1 1 0

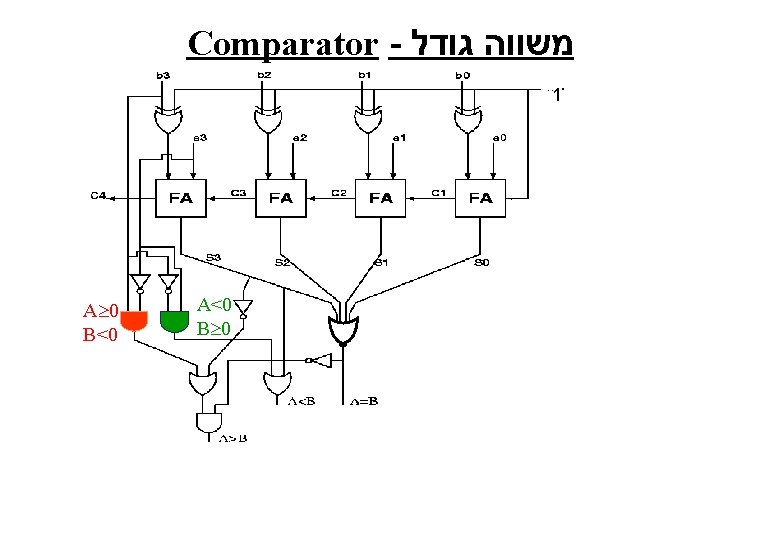
Comparator - משווה גודל 1 A 0 B<0 A<0 B 0



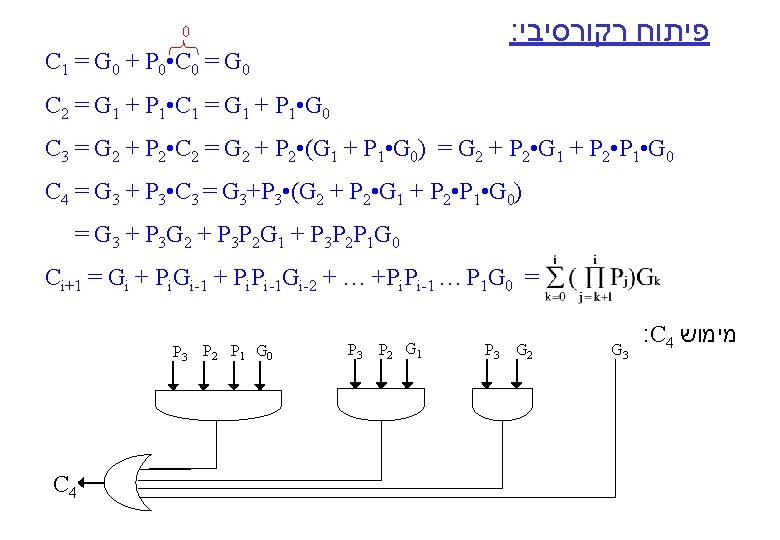
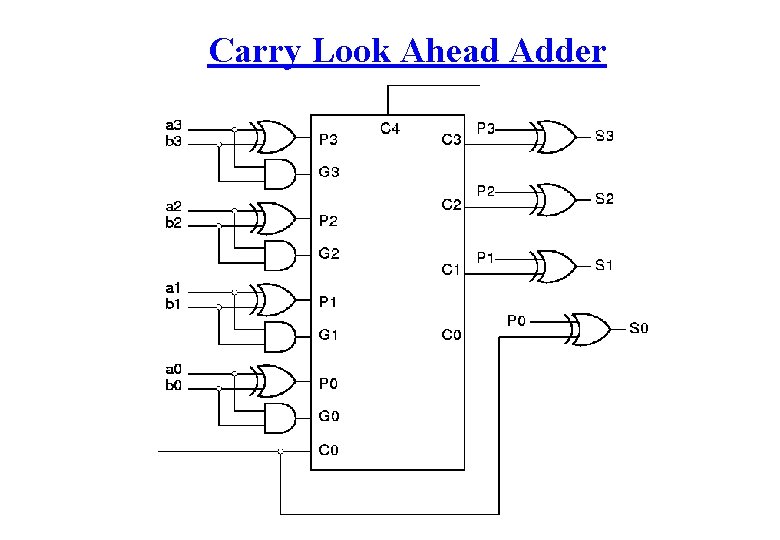
: פיתוח רקורסיבי 0 C 1 = G 0 + P 0 • C 0 = G 0 C 2 = G 1 + P 1 • C 1 = G 1 + P 1 • G 0 C 3 = G 2 + P 2 • C 2 = G 2 + P 2 • (G 1 + P 1 • G 0) = G 2 + P 2 • G 1 + P 2 • P 1 • G 0 C 4 = G 3 + P 3 • C 3 = G 3+P 3 • (G 2 + P 2 • G 1 + P 2 • P 1 • G 0) = G 3 + P 3 G 2 + P 3 P 2 G 1 + P 3 P 2 P 1 G 0 Ci+1 = Gi + Pi. Gi-1 + Pi. Pi-1 Gi-2 + … +Pi. Pi-1 … P 1 G 0 = P 3 C 4 P 2 P 1 G 0 P 3 P 2 G 1 P 3 G 2 G 3 : C 4 מימוש




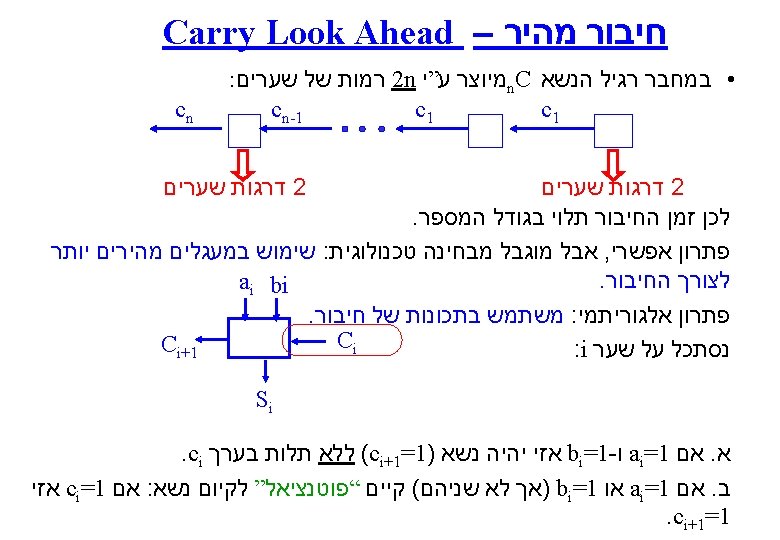
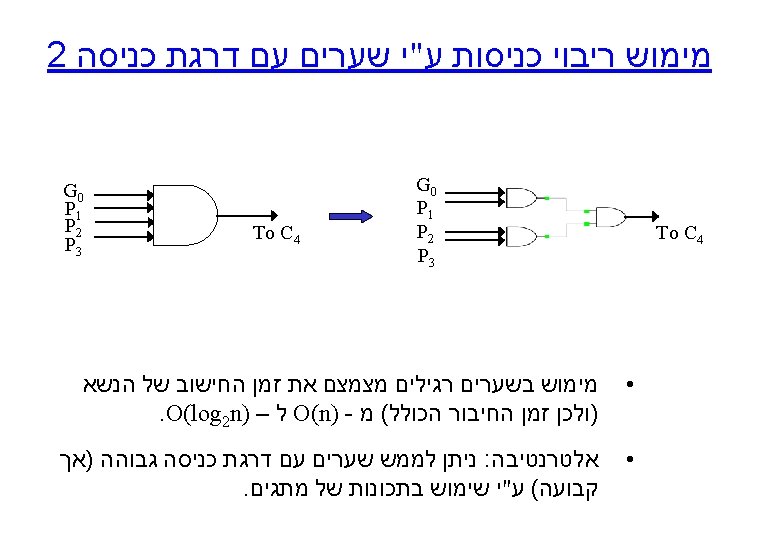
Carry Look Ahead Adder


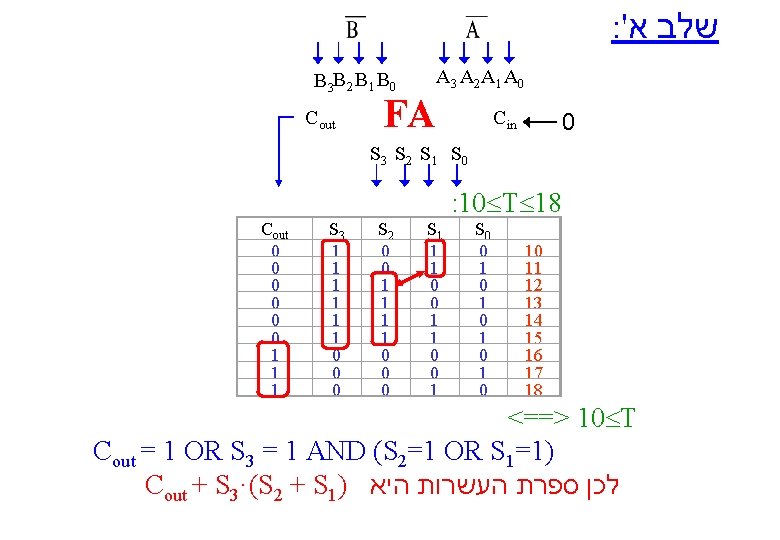
: ' שלב א B 3 B 2 B 1 B 0 Cout FA A 3 A 2 A 1 A 0 Cin 0 S 3 S 2 S 1 S 0 : 10 T 18 Cout 0 0 0 1 1 1 S 3 1 1 1 0 0 0 S 2 0 0 1 1 0 0 0 S 1 1 1 0 0 1 S 0 0 1 0 1 0 10 11 12 13 14 15 16 17 18 <==> 10 T Cout = 1 OR S 3 = 1 AND (S 2=1 OR S 1=1) Cout + S 3·(S 2 + S 1) לכן ספרת העשרות היא


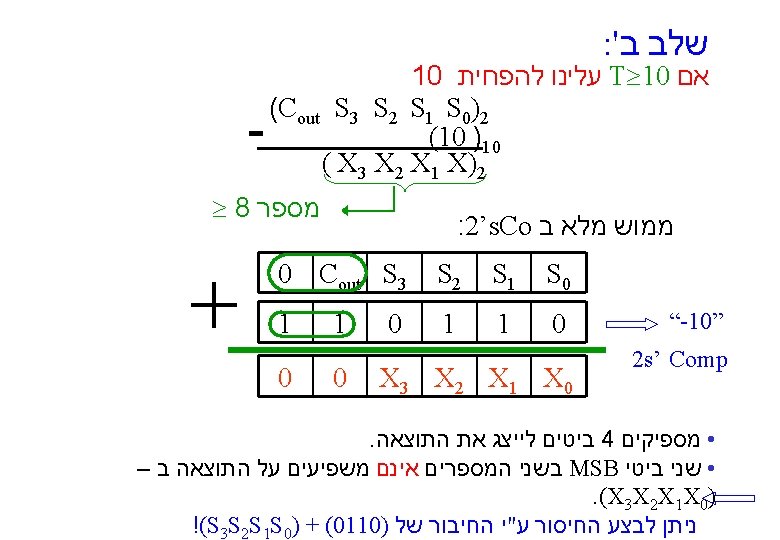
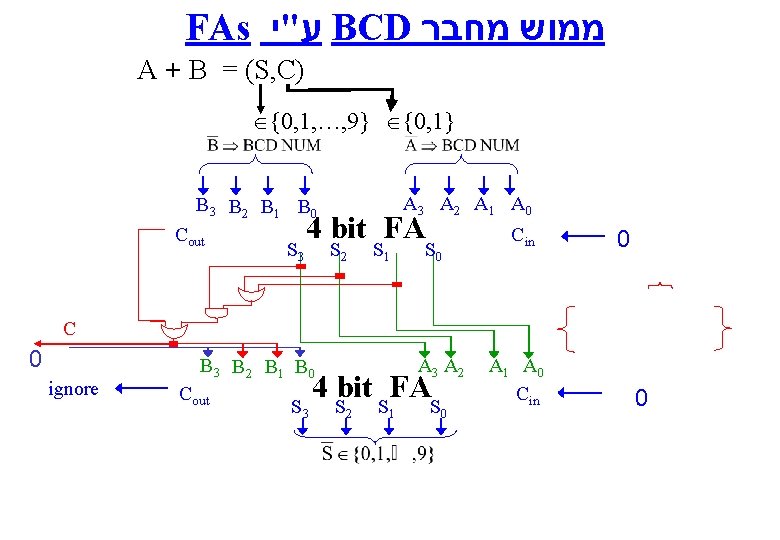
FAs ע"י BCD ממוש מחבר A + B = (S, C) {0, 1, …, 9} {0, 1} A 3 A 2 A 1 A 0 B 3 B 2 B 1 B 0 Cout S 3 4 bit FA S 2 S 1 S 0 Cin 0 C 0 ignore A 3 A 2 B 3 B 2 B 1 B 0 Cout S 3 4 bit FA S 2 S 1 S 0 A 1 A 0 Cin 0

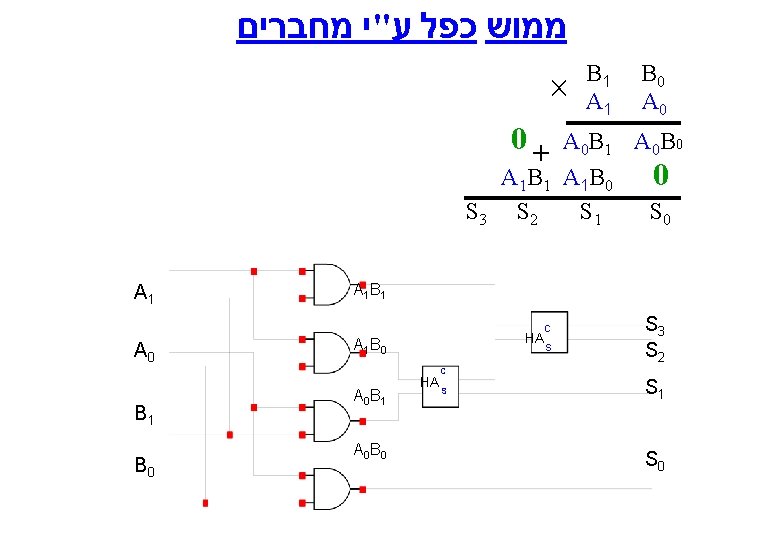
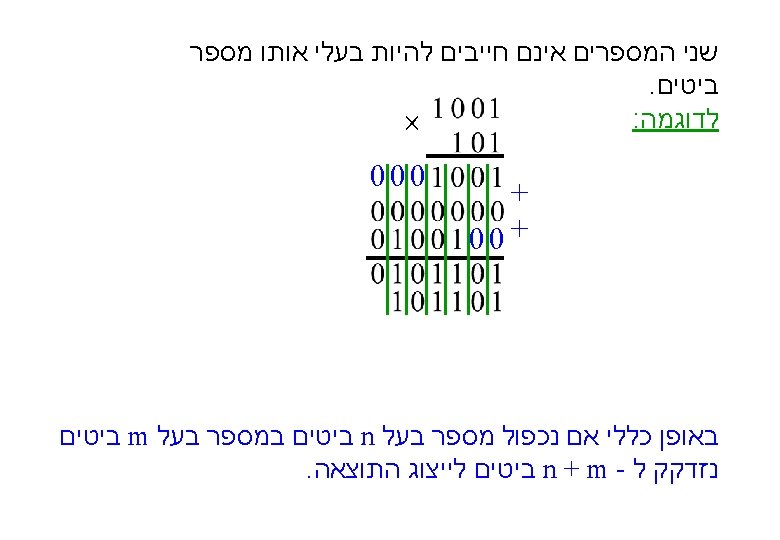
ממוש כפל ע"י מחברים 0+ B 1 A 0 B 0 A 1 B 1 A 1 B 0 S 3 S 2 S 1 A 1 B 0 0 S 0 A 1 B 1 C A 0 B 0 A 0 HA A 1 B 0 A 0 B 1 A 0 B 0 HA C S S S 3 S 2 S 1 S 0





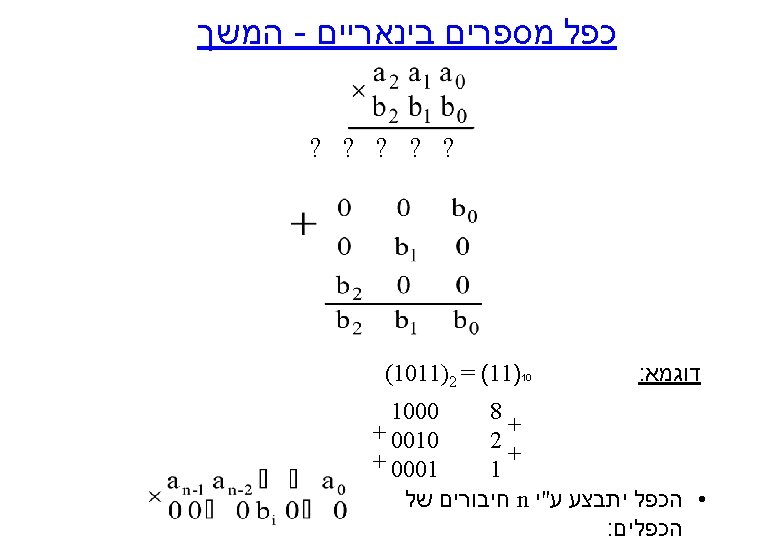
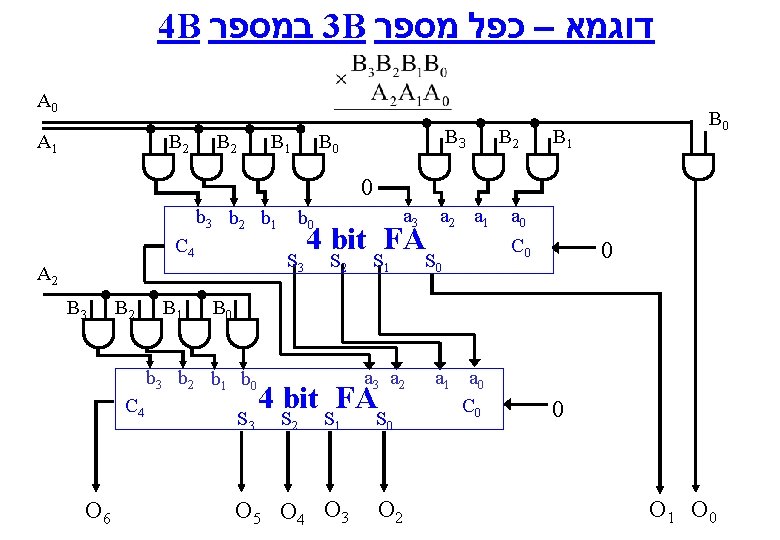
4 B במספר 3 B דוגמא – כפל מספר A 0 A 1 B 2 B 1 B 3 B 0 B 2 B 0 B 1 0 b 3 b 2 b 1 C 4 S 3 A 2 B 3 B 2 B 1 a 3 b 0 4 bit FA S 2 O 6 S 0 a 0 C 0 0 B 0 a 3 a 2 b 3 b 2 b 1 b 0 C 4 S 1 a 2 a 1 S 3 4 bit FA S 2 S 1 O 5 O 4 O 3 S 0 O 2 a 1 a 0 C 0 0 O 1 O 0