1 Viz Spark Plasma Theory and Governing Equations

1 Viz. Spark Plasma Theory and Governing Equations August 2019 1301 South Capital of Texas Hwy, Suite B-330 Austin, TX 78746, USA Web: www. esgeetech. com Email: info@esgeetech. com

2 COPYRIGHT AND CONFIDENTIALITY STATEMENT Copyright © (2007 -2019) Esgee Technologies, Inc. All rights reserved. This manual accompanies software that is provided to users under a license agreement. This manual can also be provided under a non-disclosure agreement and is subject to restrictions on confidential information under such an agreement. The manual contains proprietary information and may not be disclosed to a third party not covered by the license agreement or a non-disclosure agreement. No part of this manual may be reproduced in any form or by any means without express written permission from Esgee Technologies, Inc.

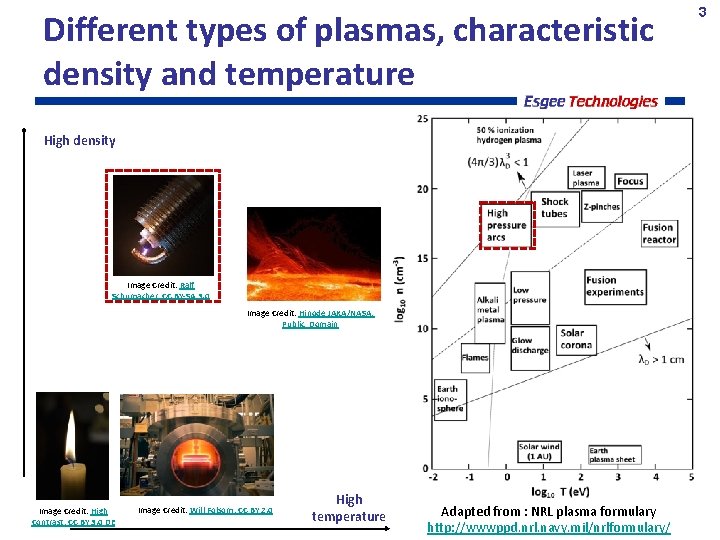
Different types of plasmas, characteristic density and temperature High density Image Credit: Ralf Schumacher, CC BY-SA 3. 0 Image Credit: Hinode JAXA/NASA, Public Domain Image Credit: High Contrast, CC BY 3. 0 DE Image Credit: Will Folsom, CC BY 2. 0 High temperature Adapted from : NRL plasma formulary http: //wwwppd. nrl. navy. mil/nrlformulary/ 3

From gas to plasma “Hot” and “Cold” plasmas 4 § Thermal plasmas (“Hot”) § Produced when gases are at extremely high temperature (~10000 K and more) § All species can be characterized by the same temperature (in thermal equilibrium) § Non-thermal plasmas (“Cold”) § Produced when electrical power is supplied to gases (gas breakdown), power is mainly absorbed by electrons § Electrons have high temperature (~10000 K and more) § Ions and Neutrals remain at lower temperature (~300 -1000 K) § Not in thermal equilibrium (non -equilibrium plasma) Image Credit: Hinode JAXA/NASA, Public Domain Image Credit: Will Folsom, CC BY 2. 0

Deviations from Thermal Equilibrium in Arc Plasma 5 § Even “thermal” plasmas like arc discharges can display non-equilibrium behavior. § Non-equilibrium behavior in thermal arcs is typically confined to the sheaths which are very thin (submicron). § Non-equilibrium effects however can be important because they determine electrical conductivity. § Hot electrons near arc root important for carrying charge § Some arc plasma codes solve two-temperature equation to account for non-equilibrium regions.

6 Magnetohydrodynamics Model • Viz. Spark is a single fluid, single temperature, resistive magnetohydroynamic (MHD) plasma model. The plasma is modelled as a single compressible, conducting, reactive fluid in chemical and thermal equilibrium. Appropriate when collisions are dominant (electrons and ions forced to act in unison as a single “fluid”) Applications include § § § Solar plasma Interstellar medium Thermal arc plasma Fusion plasma Conducting fluids (salt water) • An MHD model follows from fluid theory and Maxwell’s equations after making several approximations

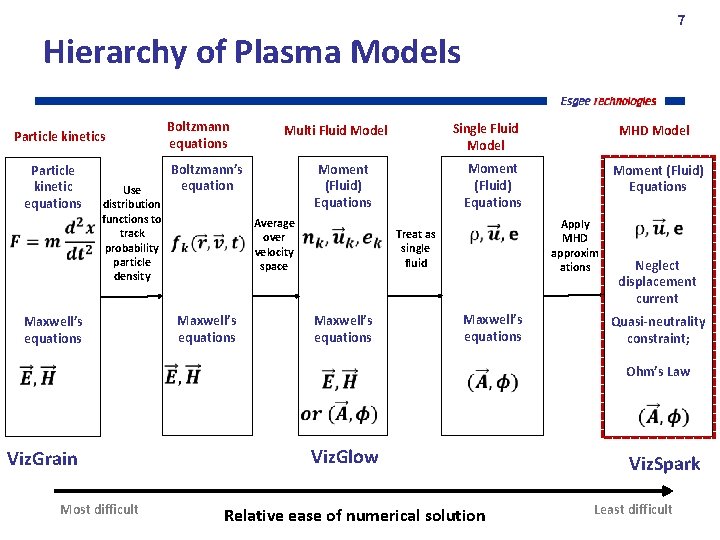
7 Hierarchy of Plasma Models Particle kinetic equations Use distribution functions to track probability particle density Maxwell’s equations Boltzmann’s equation Maxwell’s equations Viz. Grain Most difficult MHD Model Moment (Fluid) Equations Average over velocity space Single Fluid Model Multi Fluid Model Treat as single fluid Moment (Fluid) Equations Apply MHD approxim ations Neglect displacement current Maxwell’s equations Quasi-neutrality constraint; Ohm’s Law Viz. Glow Viz. Spark Relative ease of numerical solution Least difficult

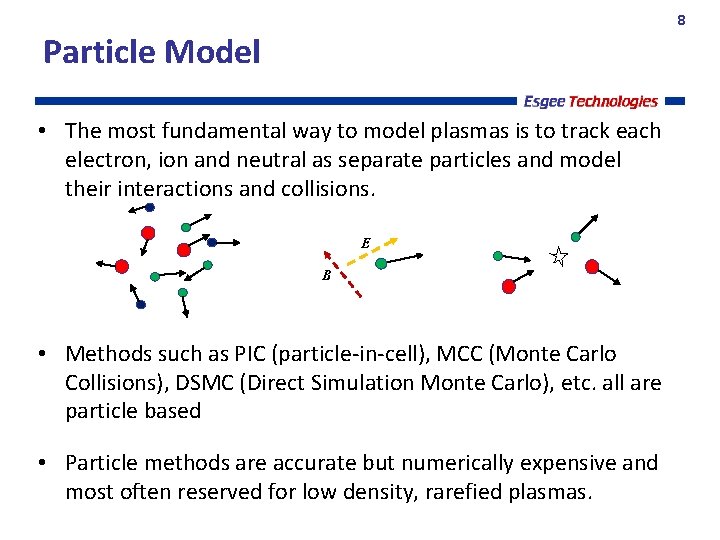
8 Particle Model • The most fundamental way to model plasmas is to track each electron, ion and neutral as separate particles and model their interactions and collisions. E B • Methods such as PIC (particle-in-cell), MCC (Monte Carlo Collisions), DSMC (Direct Simulation Monte Carlo), etc. all are particle based • Particle methods are accurate but numerically expensive and most often reserved for low density, rarefied plasmas.

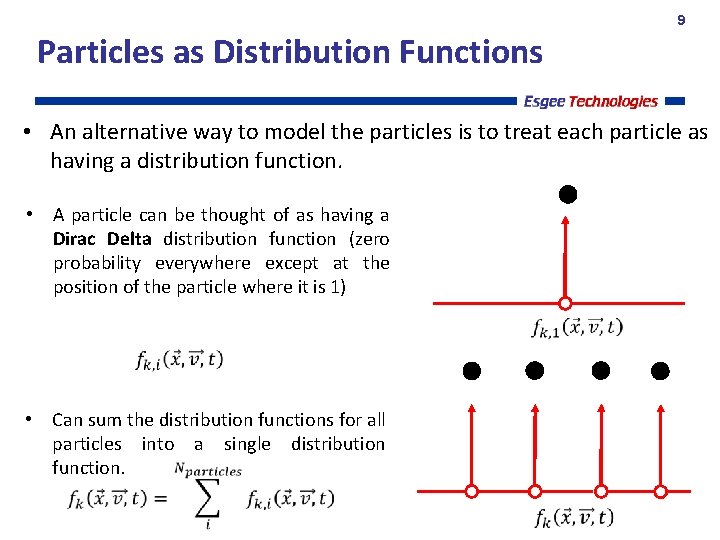
9 Particles as Distribution Functions • An alternative way to model the particles is to treat each particle as having a distribution function. • A particle can be thought of as having a Dirac Delta distribution function (zero probability everywhere except at the position of the particle where it is 1) • Can sum the distribution functions for all particles into a single distribution function.

10 Distribution Function Equation • The governing equation for the particle distribution function in phase space is • The above says that the total rate of change or total derivative of the particle distribution is due to velocity and acceleration forces. • The above formulation is still as expensive as the particle model, since we are tracking multiple distribution functions (instead of particles).

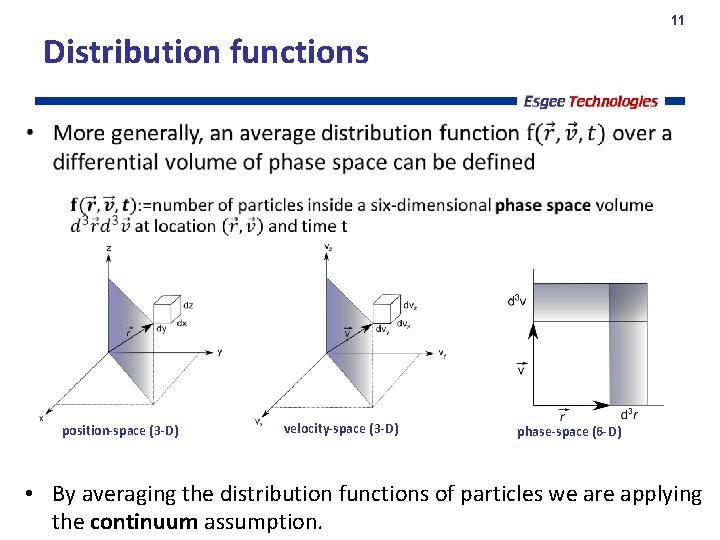
11 Distribution functions position-space (3 -D) velocity-space (3 -D) phase-space (6 -D) • By averaging the distribution functions of particles we are applying the continuum assumption.

The Boltzmann equation and fluid equations 12 • The Boltzmann Equation is a continuity equation in phase space with the species distribution function as the dependent variable • The acceleration terms are due to all forces (electromagnetic, gravity, body forces, etc. ) acting on the particles

Moments of the Distribution Function and the Boltzmann Equation 13 • One can obtain fluid averaged properties by taking moments of the distribution function. • We can obtain fluid equations (PDE’s governing how the fluid averaged properties change) by taking moments of the Boltzmann equation.

Macroscopic Properties : Moments of the Distribution Function • 0 th Moments species number density species mass density species charge density mean mass density mean charge density 14

Macroscopic Properties : Moments of the Distribution Function • 1 st Moments species average flow velocity peculiar velocity/random velocity species current density mean-mass flow velocity mean current density 15

Macroscopic Properties : Moments of the Distribution Function • 2 nd Moments species energy density momentum tensor pressure tensor 16

17 Multiple Species Fluid Model • By taking moments of the Boltzmann equation can obtain fluid equations for mass, momentum and energy conservation • 0 th Moment (conservation of species mass) • 1 st Moment (conservation of species momentum) • 2 nd Moment (conservation of species thermal energy)

18 Single Fluid Model • By adding each species mass, momentum and energy equation together can obtain single fluid model for plasma fluid Conservation of mass Conservation of momentum Conservation of energy By conservation of mass/momentum/energy all the species specific production and destruction terms sum to zero.

19 Pressure Tensor for Newtonian Fluid • The pressure tensor is related to the random motion of the plasma particles. Split the pressure tensor into an isotropic term (the gas pressure) and a viscous stress tensor term The stress tensor can be expressed as a linear function of viscosity and velocity gradients. Here we assume the plasma behaves as a Newtonian (linear) fluid

20 Thermal and Caloric Equations of State • Need a way to relate density , velocities and internal energy to the pressure and temperature of the gas. Use thermal and caloric equations of state • Thermal equation of state: • Caloric equation of state: • For special case of a perfect gas Thermal equation of state (Ideal gas law) Caloric equation of state

21 Maxwell Equations • Fluid equations are functions of electric and magnetic fields which are governed by Maxwell’s equations. § Faraday’s Law § Ampere’s Law § Gauss Law for Magnetism

22 Conservation of Charge • An equation for the conservation of charge can be derived from either fluid equations or Maxwell equations 1) From the species conservation equations. multiply each species mass conservation equation by its charge divided by mass and sum together Define charge density as since and current density is Which says charge is neither created nor destroyed, only conserved

23 Conservation of Charge 2) From Maxwell’s equations (using Gauss Law, Ampere’s Law, and Gauss Law for Magnetism. Take time derivative of Gauss Law Then from Ampere’s Law Which after rearranging derivatives is or

24 Ohm’s Law • The above equation is the one most often referred to as Ohm’s Law.

25 Ohm’s Law

26 Electromagnetic Potentials • Express electric and magnetic fields as functions of scalar and vector potentials Magnetic vector potential The Coulomb gauge

27 Electromagnetic Potentials • Insert the magnetic vector potential into Faraday’s Law and rearrange • Hence, electric field can be expressed as a function of some scalar potential, and the magnetic vector potential.

28 Magnetic Transport Equation • Magnetic field transport equation can be derived by combining the two Maxwell Curl equations(Ampere and Faraday law) magnetic induction equation

29 The Magnetohydrodynamic Approximation • Three approximations can be made to simplify the single fluid and electromagnetic governing equations, called the MHD approximation 1. Charge quasi-neutrality: 2. Neglect displacement current: 3. Use generalized Ohm’s law (without Hall current)

30 1) Charge Quasi-neutrality • In a dense, highly collisional plasma the electron Debye length will be very small so in most regions of the plasma quasineutrality holds. • The charge conservation equation becomes the current continuity equation • Electrostatic forcing term (which depends on charge density) is also neglected

31 Time and Length Scale • The advantage of assuming that the plasma is quasi-neutral is that we are no longer constrained by the plasma Debye length and electron frequency timescale. • At high plasma densities, if we tried to resolve the electron dynamics we would need to resolve Debye lengths on the order of microns or smaller and timesteps of the order of picoseconds. • The MHD equations however are only constrained by fluid time and length scales which are typically many orders of magnitude larger then the Debye length and plasma frequency.

32 2) Neglect displacement current • Using scaling argument, we can show that displacement current term is only important when considering phenomena with velocities near speed of light Define scales for the quantities : E, B, L, T, V Compare magnitude of displacement current to curl of B Neglect the displacement current if velocity scale much less then speed of light

33 3) Ohm’s Law Approximation • The Ohm’s law can be used with or without the Hall current term. In practice, it can usually be neglected and Ohm’s law becomes • If the plasma is infinitely conductive, then the term on the RHS will dominate and Ohm’s law reduces to an even simpler form. The infinite conductivity assumption is often referred to as ideal MHD model.

34 Full Set of Governing Equations § Fluid governing equations Conservation of total mass Conservation of momentum Conservation of thermal energy § Electromagnetic governing equations Magnetic induction Conservation of current (charge)

35 Full Set of Governing Equations § Fluid constitutive relations Newtonian fluid with Stokes Hypothesis Newtonian fluid with Stoke’s hypothesis applied Fourier’s Heat Law § Electromagnetic constitutive relations Electric and Magnetic Potentials Ohms Law

36 References J. A. Bittencourt, “Fundamentals of Plasma Physics, Third Edition”, Springer Verlag, New York, 2004. § Derivations of multi fluid and single fluid MHD equations

37 End of presentation www. esgeetech. com