1 VI Tri par tas Notion de tas

1 VI. Tri par tas

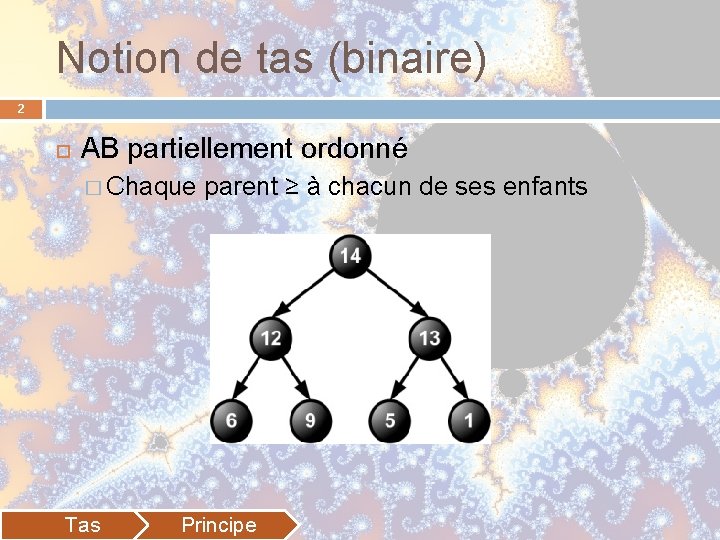
Notion de tas (binaire) 2 AB partiellement ordonné � Chaque Tas parent ≥ à chacun de ses enfants Principe

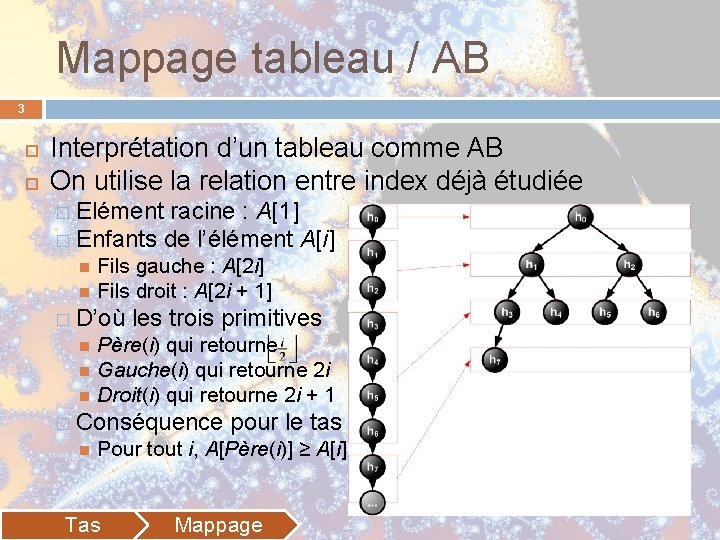
Mappage tableau / AB 3 Interprétation d’un tableau comme AB On utilise la relation entre index déjà étudiée � Elément racine : A[1] � Enfants de l’élément A[i] Fils gauche : A[2 i] Fils droit : A[2 i + 1] � D’où les trois primitives Père(i) qui retourne Gauche(i) qui retourne 2 i Droit(i) qui retourne 2 i + 1 � Conséquence pour le tas Pour tout i, A[Père(i)] ≥ A[i] Tas Mappage

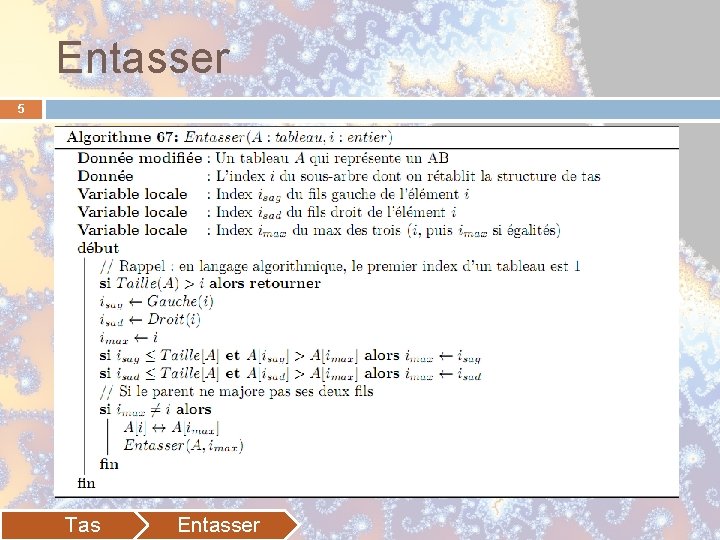
Entasser 4 Utilitaire fondamentale du tri par tas � Transforme un arbre (un sous-arbre) en tas � Principe Si la racine est majorée par l’un de ses deux fils (ou les 2) La Tas Alors permutation du parent avec le plus grand fils Peut entrainer la rupture de la structure de tas du sousarbre représenté par le fils appel récursif de la procédure sur le fils impacté complexité est évidemment logarithmique Entasser

Entasser 5 Tas Entasser

Construire un tas 6 C’est appliquer la procédure Entasser à tous les sous-arbres en remontant de celui d’index max à l’arbre principal d’index 1 � Petite optimisation Appliquer Entasser à une feuille est inutile Quel est l’index du dernier nœud qui n’est pas une feuille ? Tas Construire le

Construire un tas 7 Note sur complexité � Une borne évidente est O(nlnn) � Mais elle n’est pas optimale ! � Pas le temps de la démonstration ( littérature) � Elle est en O(n) Tas Construire le

Tri par tas 8 Propriété : dans un tas, l’élément maximum est au sommet (racine) 1. Construire. Tas � Pour amener le maximum en première position du table (racine) 2. On extrait (mémorise) ce maximum � Transposition du premier et du dernier éléments du tableau Echange de A[1] et A[A. taille] et A. taille – 1 3. On répète Entasser (et non 1. ) sur la racine A[1] suivi de 2. � Cela entraîne la rupture de tas au niveau de la racine En revanche, tous les autres nœuds restent des tas !! Tant que A. taille > 1 A l’issue de ce traitement, A est trié en ordre croissant Complexité : O(nlnn) Tas Tri par tas

Tri par tas 9 Tas Tri par tas

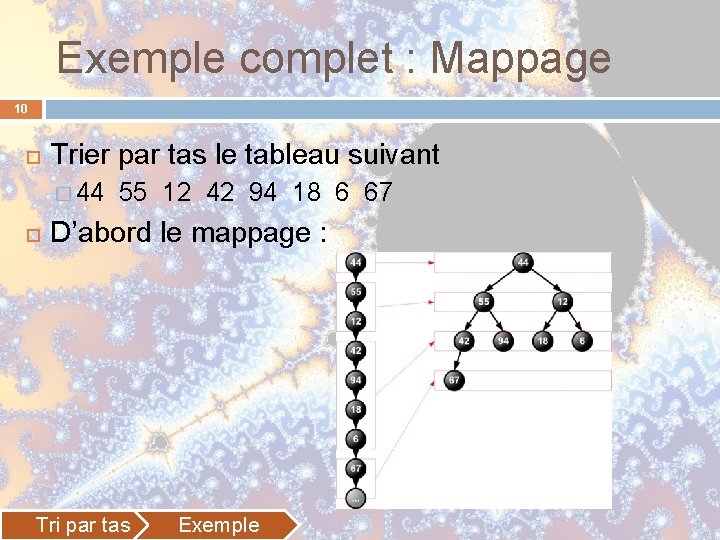
Exemple complet : Mappage 10 Trier par tas le tableau suivant � 44 55 12 42 94 18 6 67 D’abord le mappage : Tri par tas Exemple

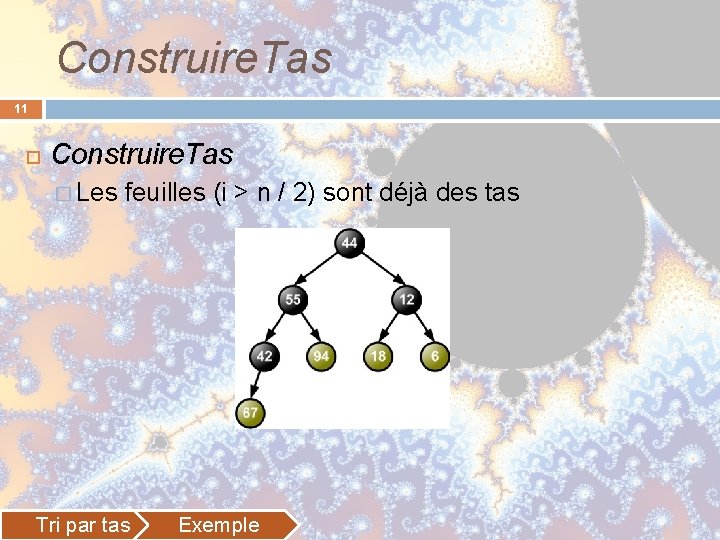
Construire. Tas 11 Construire. Tas � Les feuilles (i > n / 2) sont déjà des tas Tri par tas Exemple

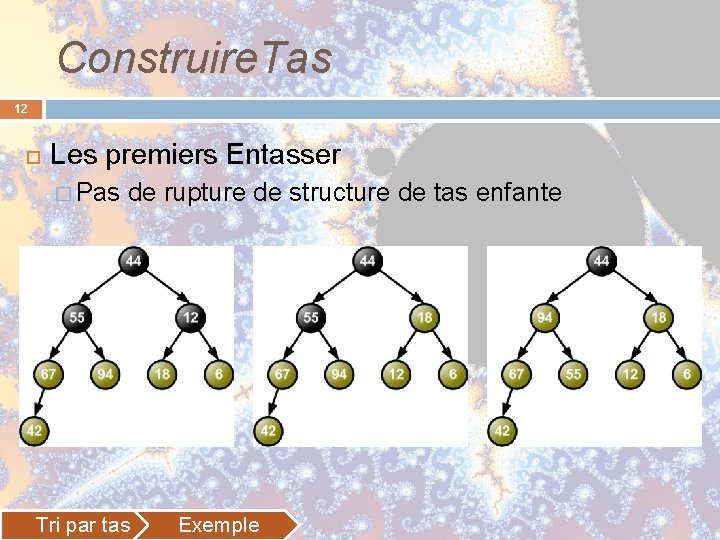
Construire. Tas 12 Les premiers Entasser � Pas de rupture de structure de tas enfante Tri par tas Exemple

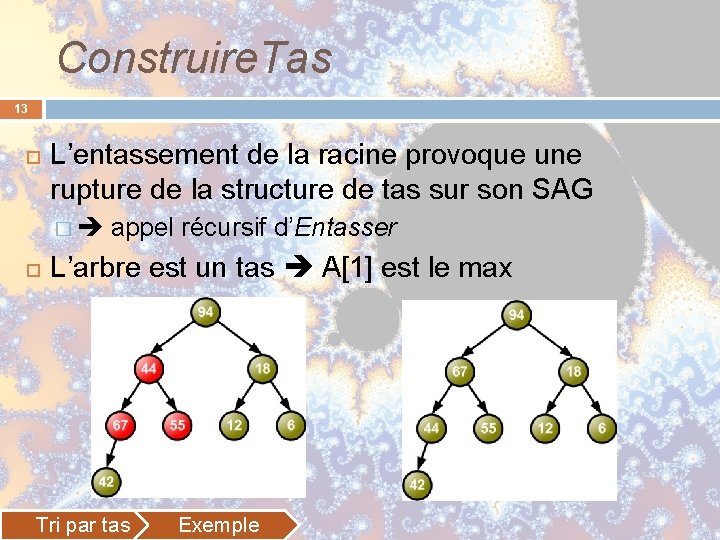
Construire. Tas 13 L’entassement de la racine provoque une rupture de la structure de tas sur son SAG � appel récursif d’Entasser L’arbre est un tas A[1] est le max Tri par tas Exemple

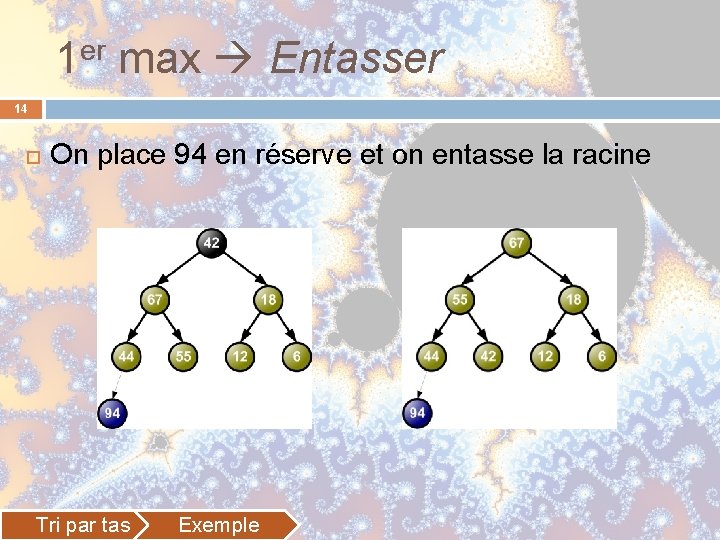
1 er max Entasser 14 On place 94 en réserve et on entasse la racine Tri par tas Exemple

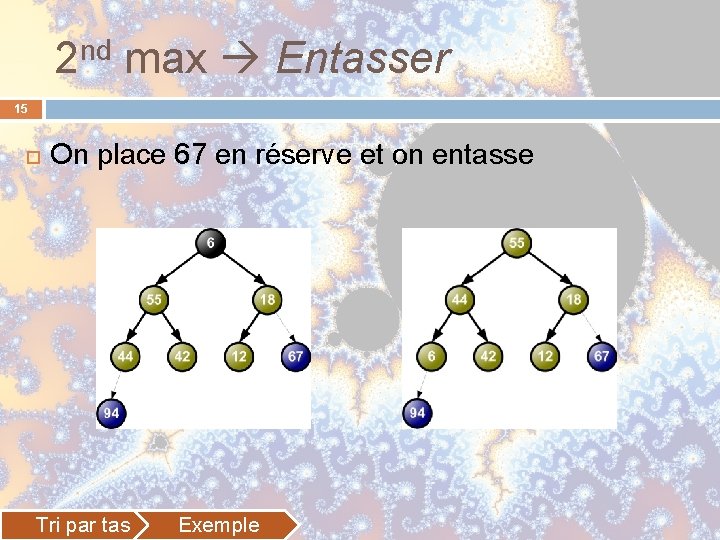
2 nd max Entasser 15 On place 67 en réserve et on entasse Tri par tas Exemple

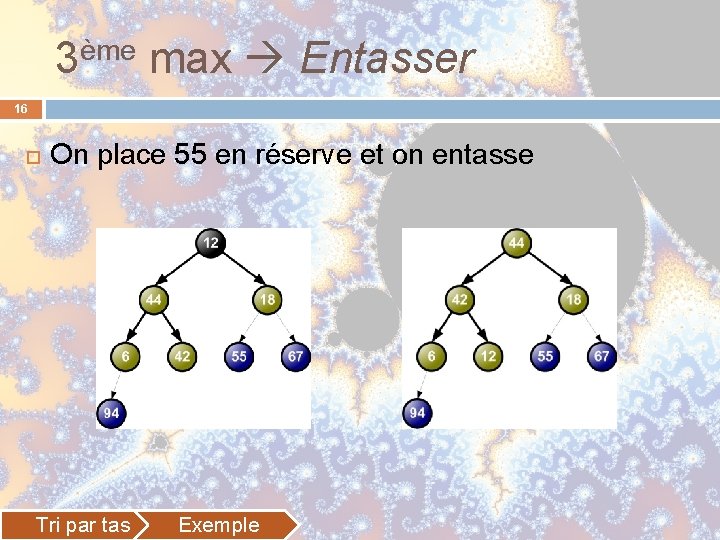
3ème max Entasser 16 On place 55 en réserve et on entasse Tri par tas Exemple

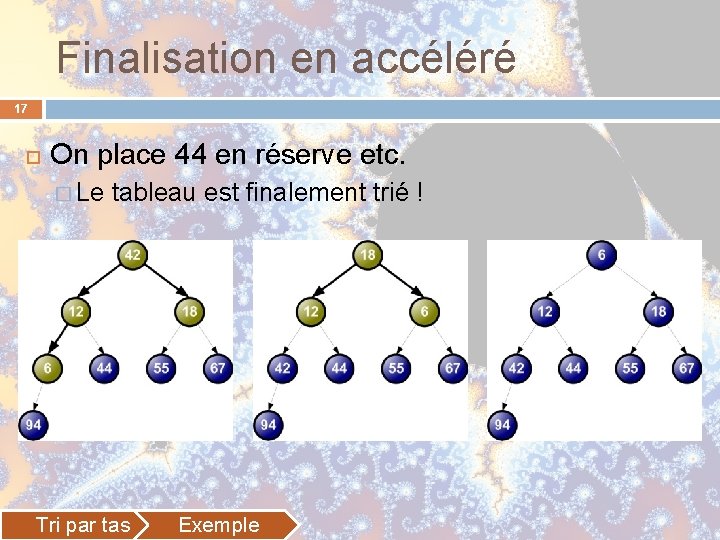
Finalisation en accéléré 17 On place 44 en réserve etc. � Le tableau est finalement trié ! Tri par tas Exemple