1 Variables Artificiales Son variables binarias o variables

1 Variables Artificiales Son variables binarias o variables cero-uno diseñadas para describir informacion cualitativa

2

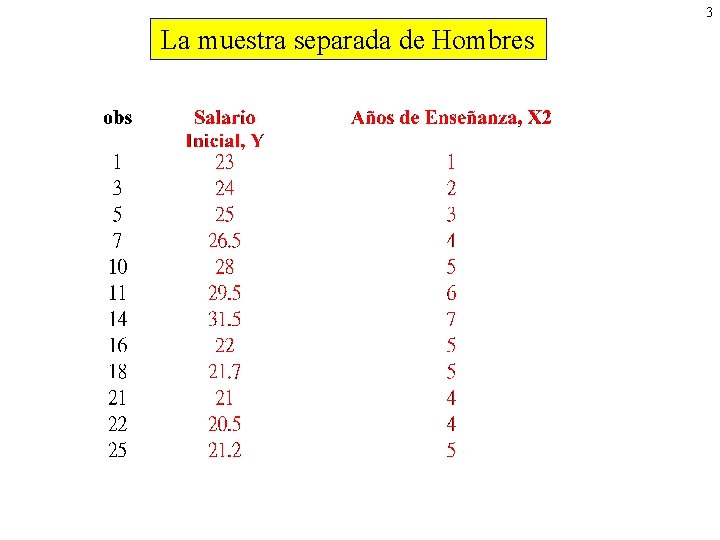
3 La muestra separada de Hombres

4 La muestra separada de Mujeres

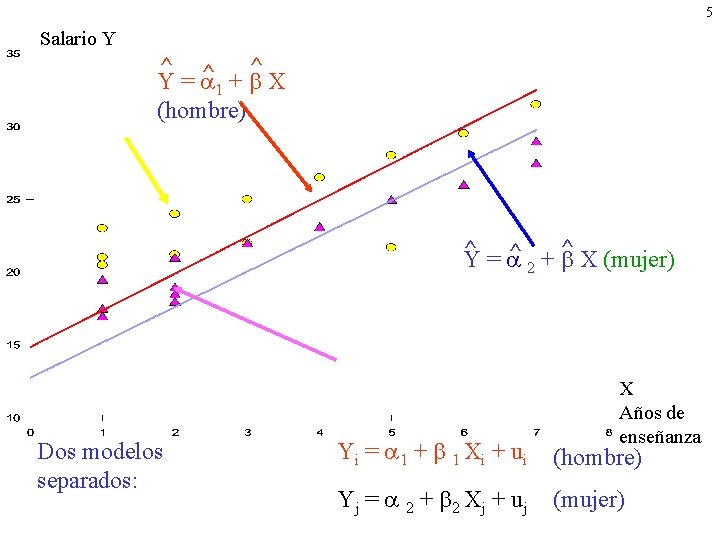
5 Salario Y ^ ^ ^ Y = 1 + X (hombre) ^ ^ +^ Y= X (mujer) 2 Dos modelos separados: X Años de enseñanza Yi = 1 + 1 Xi + u i (hombre) Yj = 2 + 2 Xj + u j (mujer)

Supongamos que la relacion entre Y y X no cambia, es decir, las pendientes son las mismas: 1 = 2. Modelo: Yi = 1 + 2 Di + Xi + u i Supongamos que la relacion entre Y y X cambia, es decir, las pendientes no son las mismas: 1 2. Yi = 1 + 2 Di + Xi + D*Xi + ui Modelo: Yi = salario anual Xi = años de esperiencia enseñando Di = 1 =0 si hombre en caso contrario (mujer) Variable de control 6

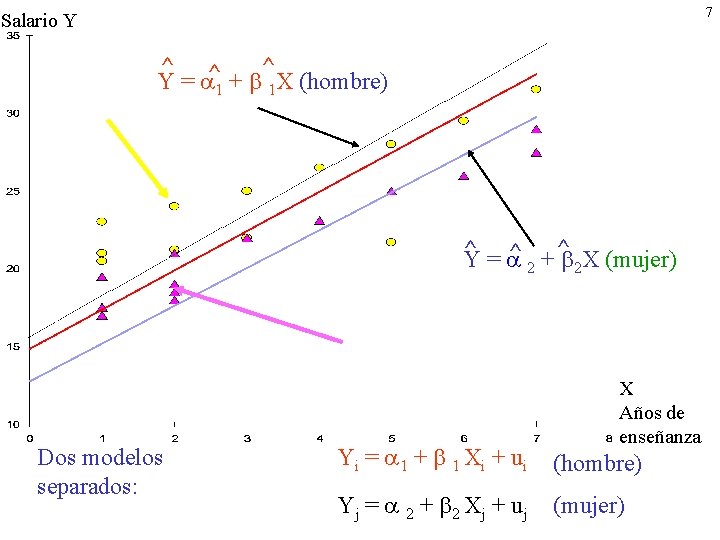
7 Salario Y ^ ^ ^ Y = 1 + 1 X (hombre) ^ ^ + ^ X (mujer) Y= 2 2 Dos modelos separados: X Años de enseñanza Yi = 1 + 1 Xi + u i (hombre) Yj = 2 + 2 Xj + u j (mujer)

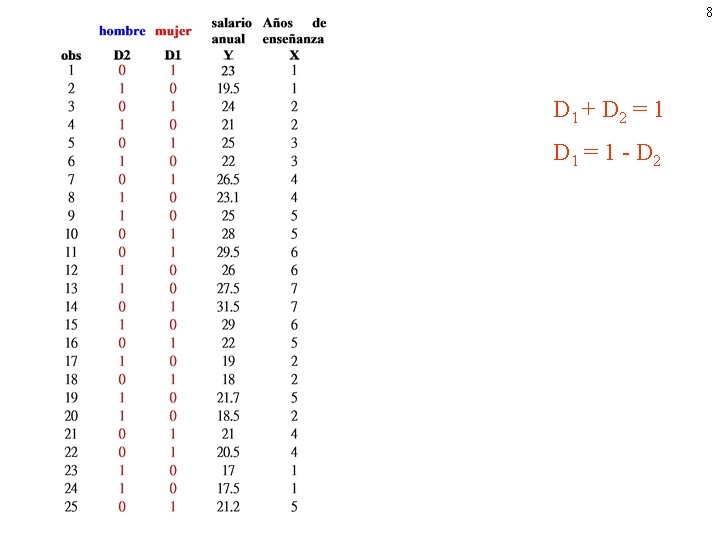
8 D 1 + D 2 = 1 D 1 = 1 - D 2

9 (La Trampa de la Variable Dummy) Si se introducen dos variables dummies en un modelo como Yi = 1 + 2 D 1 i + 2 D 2 i + Xi + u. I donde D 1 i = 1 hombre = 0 lo contrario donde D 2 i = 1 mujer = 0 lo contrario, entonces este modelo no se puede estimar debido a la existencia de multicolinealidad perfecta entre la constante, D 1 y D 2. D 1 = 1 - D 2 o D 2 = 1 - D 1 o D 1 + D 2 = 1 ( Multicolinealidad Perfecta)

10 1 2 Para evitar la multicolinealidad perfecta, si una variable cualitativa tiene “m” categorias, introducir solo “m-1” variables dummies. Cuando a una de las categorias de una variable dummy se le asigna el valor de cero se la llama categoria-control (o grupo omitido).

11 Volvamos al ejemplo del principio: Yi = 1 + 2 Di + Xi + u. I Model: Di = 1 hombre = 0 en caso contrario Hombre : Mujer: ==> ^ ^X ^ + ^ D) + Yi = ( 1 2 i i Di = 1 ^ ^ ^ Yi = 1 + Xi Di = 0

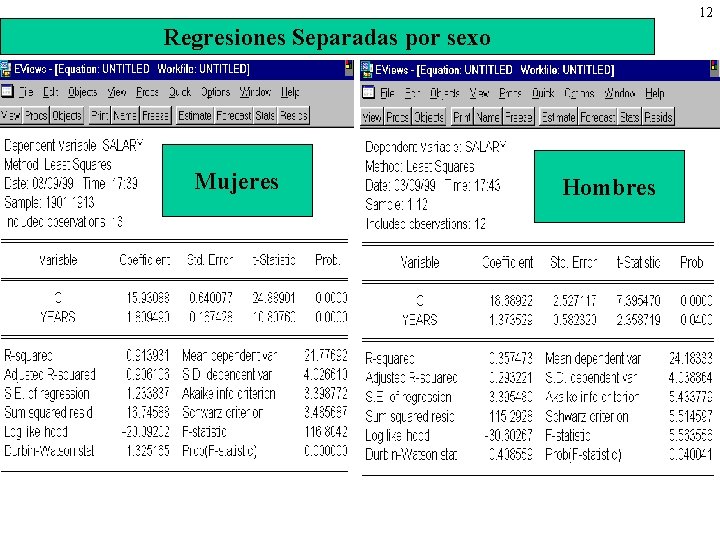
12 Regresiones Separadas por sexo Mujeres Hombres

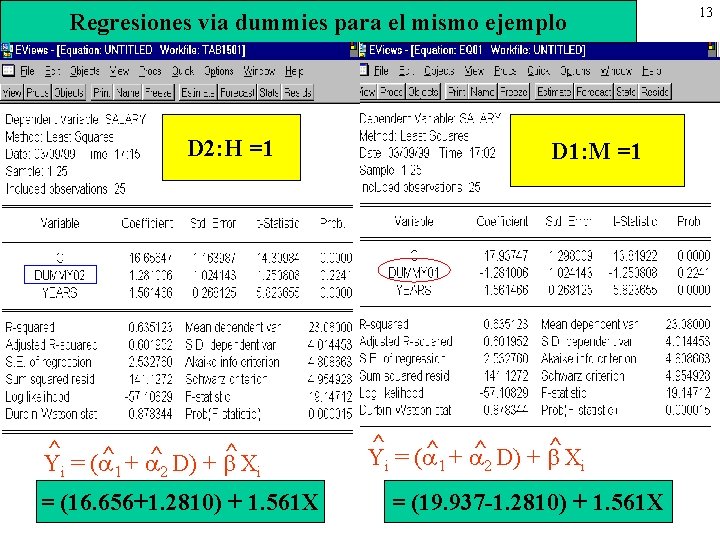
Regresiones via dummies para el mismo ejemplo D 2: H =1 ^ ^X ^ + ^ D) + Yi = ( 1 2 i = (16. 656+1. 2810) + 1. 561 X D 1: M =1 ^ ^X ^ + ^ D) + Yi = ( 1 2 i = (19. 937 -1. 2810) + 1. 561 X 13

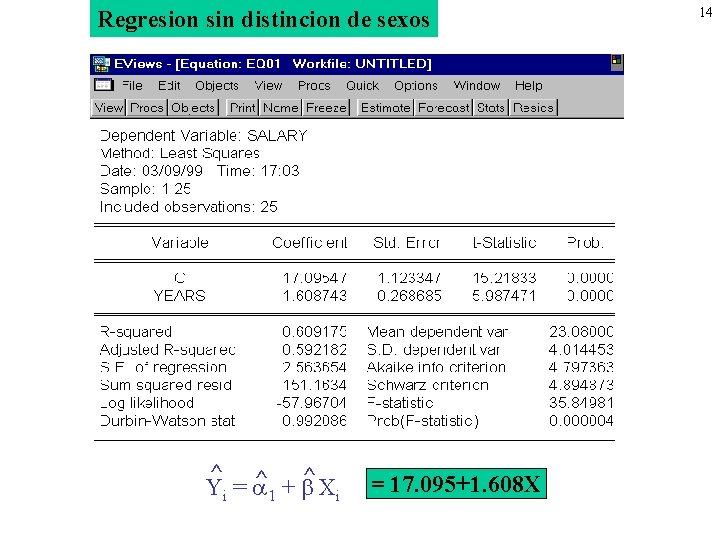
Regresion sin distincion de sexos ^ ^ ^ Yi = 1 + Xi = 17. 095+1. 608 X 14

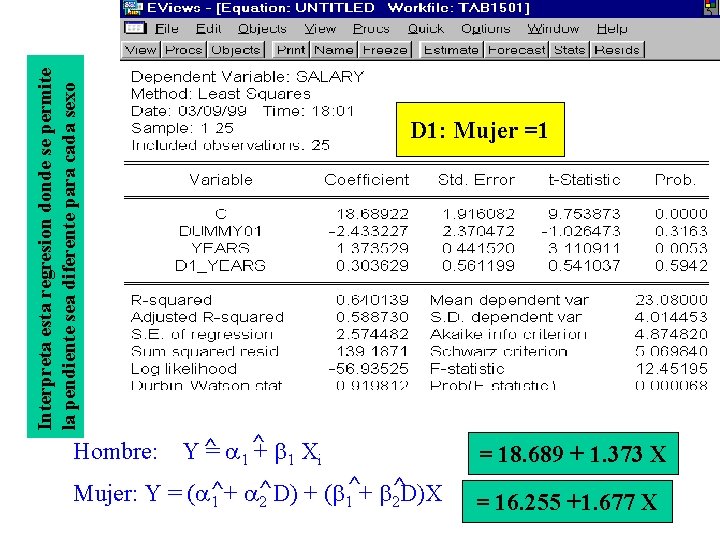
Interpreta esta regresion donde se permite la pendiente sea diferente para cada sexo 15 D 1: Mujer =1 Y ^= 1 ^+ 1 Xi = 18. 689 + 1. 373 X ^+ ^D)X ^ Mujer: Y = ( ^ + D) + ( 1 2 = 16. 255 +1. 677 X Hombre:

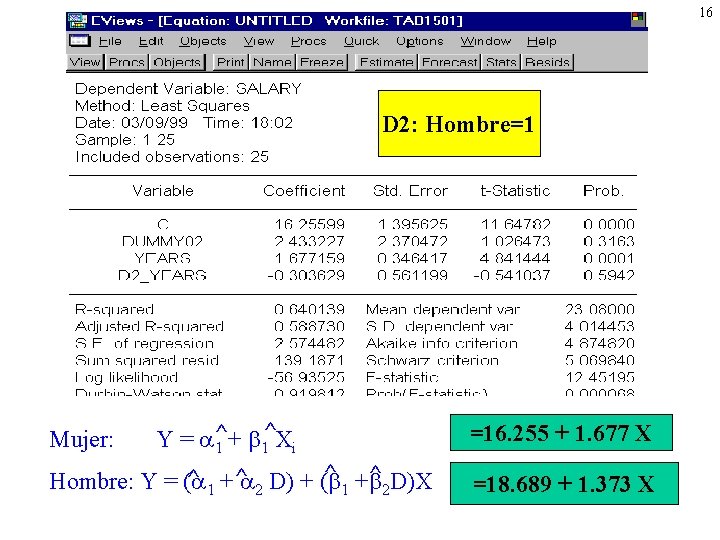
16 D 2: Hombre=1 Mujer: ^X Y = ^ + 1 1 i ^ + ^ D)X ^ 1 +^ 2 D) + ( Hombre: Y = ( 1 2 =16. 255 + 1. 677 X =18. 689 + 1. 373 X

17 Una variable cualitativa con mas de dos categorias (Y) (X) (Gasto medico) = 1 + 2 D 2 + 3 D 3 + Renta + u D 2 = 1 Educacion secundaria = 0 otros D 3 = 1 Educacion universitaria = 0 otros

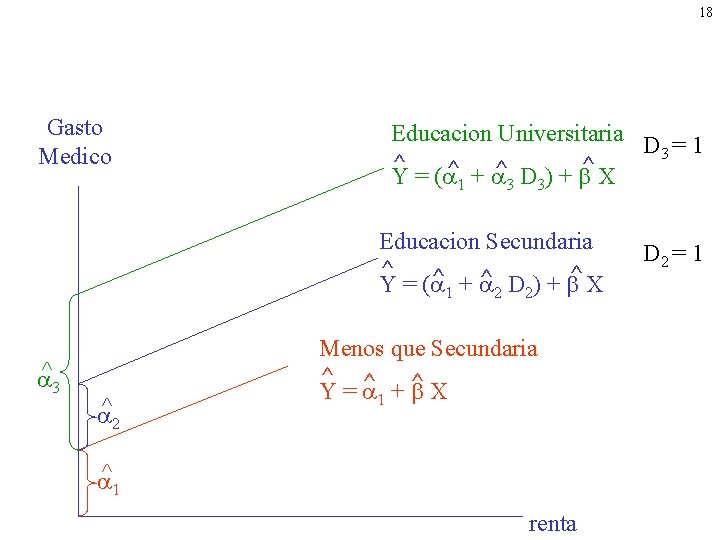
18 Gasto Medico Educacion Universitaria D 3 = 1 ^ Y = ( ^ + ^ D ) + ^ X 1 3 3 Educacion Secundaria ^ ^ + ^ D ) + ^ X Y = ( 1 ^3 ^2 2 2 Menos que Secundaria ^ ^ ^ Y= + X 1 ^1 renta D 2 = 1

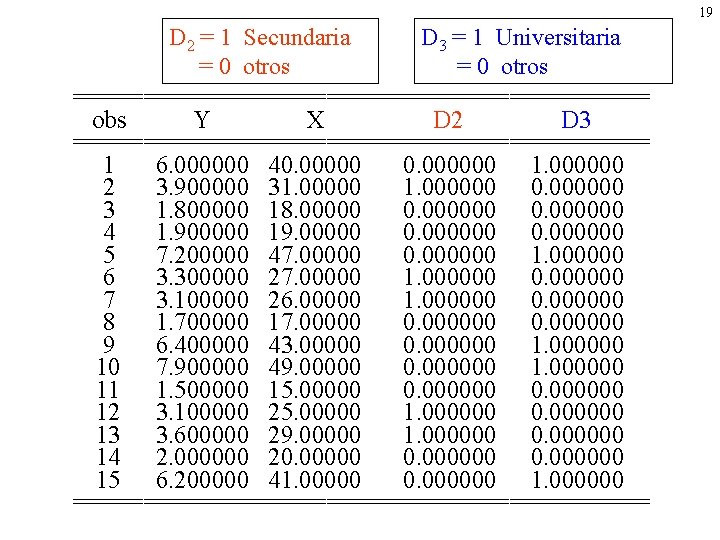
19 D 2 = 1 Secundaria D 3 = 1 Universitaria = 0 otros ===================== obs Y X D 2 D 3 ===================== 1 6. 000000 40. 000000 1. 000000 2 3. 900000 31. 000000 0. 000000 3 1. 800000 18. 00000 0. 000000 4 1. 900000 19. 00000 0. 000000 5 7. 200000 47. 00000 0. 000000 1. 000000 6 3. 300000 27. 00000 1. 000000 0. 000000 7 3. 100000 26. 00000 1. 000000 0. 000000 8 1. 700000 17. 00000 0. 000000 9 6. 400000 43. 00000 0. 000000 10 7. 900000 49. 00000 0. 000000 11 1. 500000 15. 00000 0. 000000 12 3. 100000 25. 00000 1. 000000 0. 000000 13 3. 600000 29. 00000 1. 000000 0. 000000 14 2. 000000 20. 000000 15 6. 200000 41. 00000 0. 000000 1. 000000 =====================

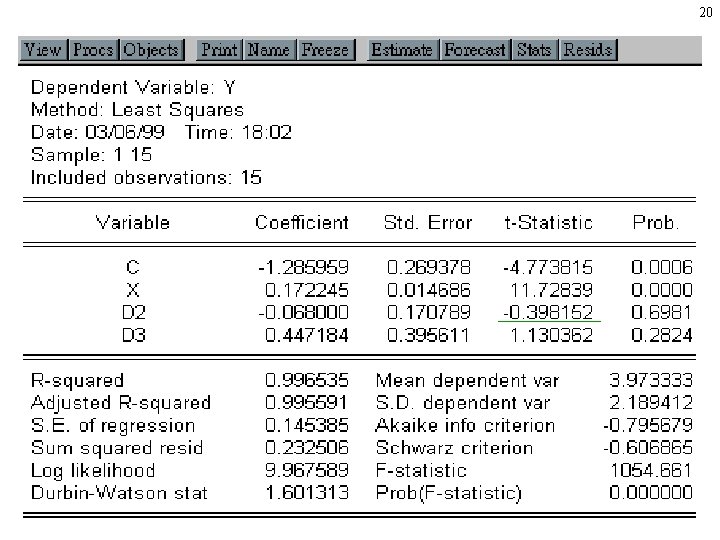
20

21 ^ Menos que secundaria: Yi = -1. 2859 + 0. 1722 Xi Secundaria: ^ = (-1. 2859 - 0. 068 ) + 0. 1722 X Y i i = -1. 3539 + 0. 1722 X = -1. 2859 + 0. 1722 X Universitari a: ^ = (-1. 2859 + 0. 447 ) + 0. 1722 X Y i i = -0. 8389 + 0. 1722 Xi = -1. 2859 + 0. 1722 X

22 Una variable cualitativa con varias categorias : Ejemplo : Un modelo para el gasto medico segun la edad Yi = 0 + 1 A 1 + 2 A 2 + Xi + u i (t-valor) donde A 1 = 1 si 55 > edad > 25 A 1 + A 2 1 = 0 otros A 2 = 1 si edad > 55 = 0 otros 0 A 1 =1 25 A 2 =1 55

23 (Cont. ) Entonces los modelos estimados son: ^ ^ ^ Menos de 25 Y = 0 + X 25 < edad < 55 edad > 55 ^ Y = ( ^0 + ^1 A 1) + ^ X ^ ^ Y = ( ^1 + ^2 A 2) + X Pensad que hipotesis pueden ser interesantes para contrastar y como hacerlo

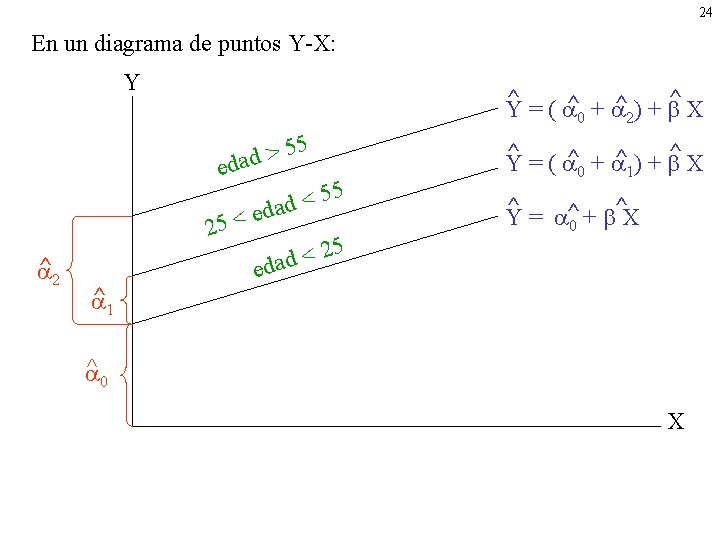
24 En un diagrama de puntos Y-X: Y ^ ^ Y = ( ^0 + ^2) + X 5 5 > d a ed 5 5 < dad e 25 < ^ 2 ^ 1 5 2 < dad ^ = ( ^ + ^ ) + ^X Y 0 1 ^ ^ Y = ^0 + X e ^ 0 X

25 Dos variables cualitativas (Y) Salario= 1 + 2 D 2 + 3 D 3 + X + u o Y = 1 + 2 D 2 + 3 D 3 + X + 1 D 2*X + 2 D 3*X + u’ D 2 = 1 =0 hombre otros sexo D 3 = 1 =0 blanca otras raza (1) Salario medio para profesoras de raza negra: ^ ^ =^ Y 1 + X es decir D 2 = 0, D 3 = 0 (2) Salario medio para profesores de raza negra: ^ = ( ^ + ^ Y es decir D 2 = 1, D 3 = 0 1 2 D 2) + X

26 (3) Salario medio para profesoras de raza blanca: ^ = ( ^ + ^ D ) + X Y 1 2 3 esto es D 2 = 0, D 3 = 1 (4) Salario medio para profesores de raza blanca: ^ = ( ^ + ^ ^ Y D + esto es D 2 = 1, D 3 = 1 1 2 2 3 D 3) + X

Diferentes tipos de regresion con variables dummies 1. Identica: Y = 1 + 2 X + 3 D + 4 D*X H 0 : 3 = 0 y 4 = 0 2. Paralela: Y = 1 + 2 X + 3 D + 4 D*X H 0 : 4 = 0 3. Concurrente: Y = 1 + 2 X + 3 D + 4 D*X H 0 : 3 = 0 4. Cruzada: Y = 1 + 2 X + 3 D + 4 D*X H 0 : 3 0 y 4 0 D = 1 si 1946 -1954 = 0 demas (1955 -1963) 27

28 Periodo (46 -54): Yt = A 1 + A 2 Xt + u 1 t (55 -63): Yt = B 1 + B 2 Xt +u 2 t Y Y 1 A 2 = B 2 B 1 1 A 1 = B 1 X Identica 1 B 2 A 1 A 1 B 1, A 2 = B 2 Paralela X

29 Y Y A 2 1 B 2 1 1 B 1 A 1 = B 1, A 2 B 2 Concurrente A 1 X A 1 B 1, A 2 B 2 Cruzada X

30 Efectos interactivos entre dos variables cualitativas Ejemplo: Gasto(Y) = 1 + 2 D 2 + 3 D 3 + renta(X) + u D 2 = 1 mujer = 0 demas sexo D 3 = 1 estudiante universitario educacion = 0 demas Efecto Interactivo: Gasto(Y) = 1 + 2 D 2 + 3 D 3 + 4 D 2*D 3 + renta(X) + u 2 = efecto diferenciador de ser mujer 3= efecto diferenciador de ser estudiante universitario 4 = efecto diferenciador de ser mujer estudiante universitaria

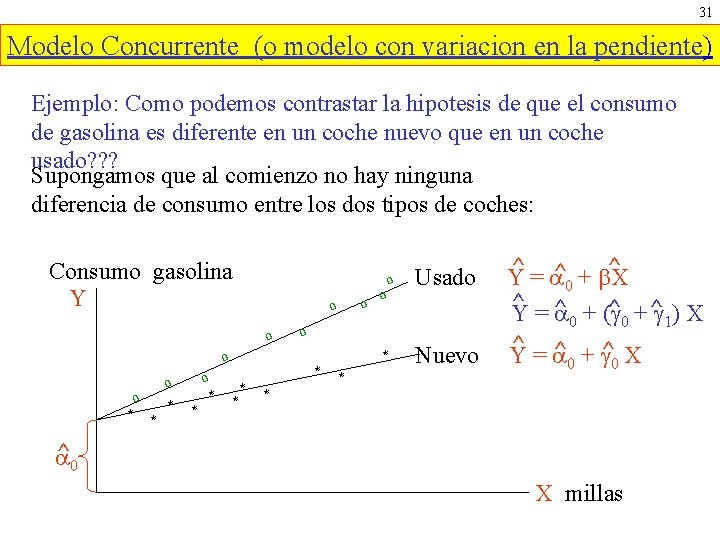
31 Modelo Concurrente (o modelo con variacion en la pendiente) Ejemplo: Como podemos contrastar la hipotesis de que el consumo de gasolina es diferente en un coche nuevo que en un coche usado? ? ? Supongamos que al comienzo no hay ninguna diferencia de consumo entre los dos tipos de coches: Consumo gasolina Y o o o * * * * Usado * Nuevo o o * ^ = ^ + X ^ Y 0 ^ ^0 + ^ 1) X Y=^ 0 + ( ^ ^ ^ Y= 0 + 0 X * ^ 0 X millas

32 Sea = 0 + 1 D donde D = 1 coche usado = 0 otros Entonces Yi = 0 + ( 0 + 1 D) Xi +ui = 0 + 0 Xi + 1 D*Xi +ui = 0 + 0 Xi + 1 Zi +ui Variable dummy multiplicativa Las relaciones estimadas son: ^ = ^ + ^ X Nuevo : Y i 0 0 i == ^ =^ Usado: Y 0 + ( ^0 + ^1 Di) Xi i ^ = ^X ^ o Y + i 0 == i donde Di = 1

Queremos contrastar si 1 = 0 o no. Se pueden utilizar dos estrategias: ^ = ^ + ^X (i) Comparar : (a) Y 0 ^= ^0 + ^ 0 X (b) Y (ii) Usar el t-test : H 0 : 1 = 0 H 1 : 1 > 0 o ( 1 0) ^ = ^ 0 + ^0 Xi + ^1 Z Y Si t* > tc. P, N-3 => rechazar H 0 33

34 Calcular el t-valor …. . . ^ ^ ^ + ^ Y = X + 1 Z i + 0 0 i

35 Variaciones tanto en la constante como en la pendiente Ejemplo: Estimacion de efectos estacionales : E= + T+u E : consumo de electricidad T : temperatura Para capturar los efectos estacionales solo en la constante: E = 0 + 1 D 1 + 2 D 2 + 3 D 3 + T + u donde D 1 = 1 0 invierno otros D 2 = 1 0 primavera otros D 3 = 1 0 verano otros Q 1 Q 2 Q 3 Q 4 prim verano oto invier

36 Considerad ahora tambien un cambio en las pendientes por razones estacionales. = 0 + 1 D 1 + 2 D 2 + 3 D 3 Sea Entonces, el modelo completamente especificado es E = [ 0 + 1 D 1 + 2 D 2 + 3 D 3] + 0 T + 1 D 1 T + 2 D 2 T Z 1 Z 2 + D T+ 3 3 Z 3

37 Los cuatro submodelos son: ^ ^ ^ Otoño E= + T 0 0 ^ ^ ^ E = ( ^0 + ^1) + ( 0 + 1) T ^ = ( ^ + ^ ) + ( ^ + ^ ) T Primavera E 0 2 ^) T Verano E^= ( 0^+ 3^) + ( ^ + 0 3 E ^ ) + ( ^ + ^ )T (Verano) ^ + E = ( 0 3 Invierno ^ ) + ( ^ + ^ )T (Primaver) ^ + E = ( 0 1 0 2 ^ 4 ^ ^ 2 1 ^ 0 ^ ^ ^ E = ( 0 + 1) + ( ^0 + ^2)T(Invier) ^ ^ ^ E = 0 + 0 T (Otoño) T

38 Los efectos estacionales a veces se modelan como efectos trimestrales D 2 = 1 2 -- Trimestre =0 D 3 = 1 =0 D 4 = 1 =0 otros 3 -- Trimestre otros 4 -- Trimestre otros Trimestre de control es el primero

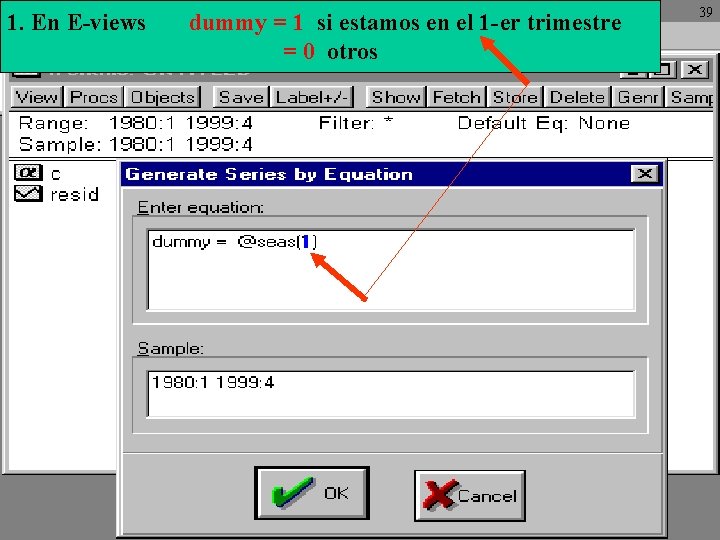
1. En E-views dummy = 1 si estamos en el 1 -er trimestre = 0 otros 39

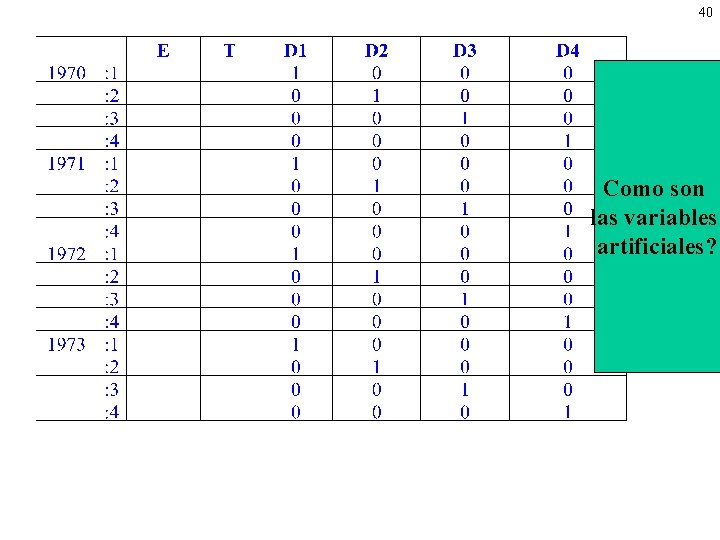
40 Como son las variables artificiales?

Contraste de Cambio Estructural basado en variables dummies Modelo Basico 1960 YT = + XT + u T Se define la variable dummy : 1989 1974 D = 1 para el periodo que va de 1974 al 1989 = 0 el resto Pra contrastar si las estructuras de los dos periodos son diferentes, la especificacion debe asumir que = 0 + 1 D = 1 + 2 D El modelo de regresion: YT = 0 + 1 D + 1 XT + 2 D X T + u T 41

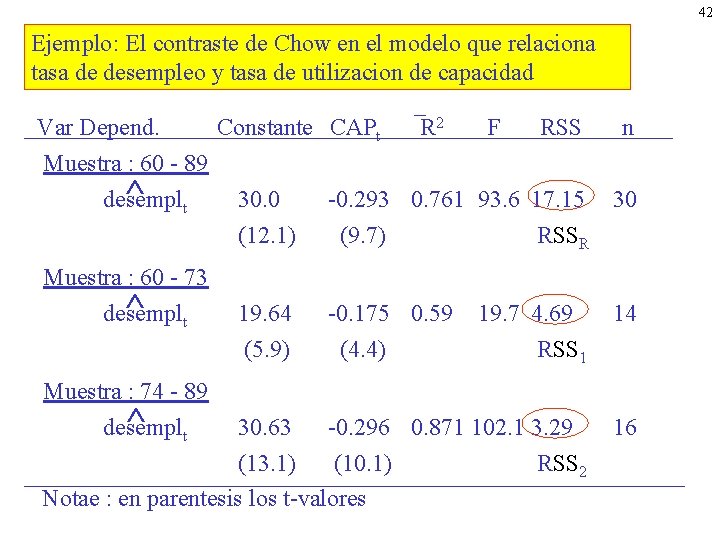
42 Ejemplo: El contraste de Chow en el modelo que relaciona tasa de desempleo y tasa de utilizacion de capacidad _ Var Depend. Constante CAPt R 2 F RSS n Muestra : 60 - 89 ^ desemplt 30. 0 (12. 1) -0. 293 0. 761 93. 6 17. 15 30 (9. 7) RSSR 19. 64 (5. 9) -0. 175 0. 59 (4. 4) Muestra : 60 - 73 ^ desemplt 19. 7 4. 69 RSS 1 14 30. 63 -0. 296 0. 871 102. 1 3. 29 (13. 1) (10. 1) RSS 2 Notae : en parentesis los t-valores 16 Muestra : 74 - 89 ^ desemplt

43 Contraste de cambio estructural via un test F: H 0 : No cambio estructural H 1 : Si Para el modelo no restringido: : RSSNR = RSS 1 + RSS 2 = 4. 69 + 3. 29 = 7. 98 F* (RSSR - RSSNR) / k = RSSNR / (T - 2 k) (17. 15 - 7. 98) / 2 = = 14. 9 7. 98 / (30 - 4) Fc 0. 01, k, T -2 k = Fc 0. 01 0. 05 = 5. 53 0. 05, 2, 26 = 3. 37 F* > Fc ==> rechazar H 0

44 Tasa de desempleo- tasa de utilizacion de capacidad Muestra : 1960 - 1989 Dt = 1 =0 1974 a 1980 antes de 1974 ^ desempl = 19. 6 + 11. 0 Dt - 0. 175 CAPt - 0. 121 (Dt*CAPt) (6. 7) (2. 7) (5. 0) (2. 5) _ R 2 = 0. 88 SEE = 0. 554 F = 72. 2 n = 30 El modelo estimado para el periodo 1960 -1973: ^ desempl = 19. 6 - 0. 175 CAP El modelo estimado para el periodo 1974 -1980: desempl = (19. 6+11. 0) - (0. 175+0. 121)CAP = 30. 6 - 0. 296 CAP ^

D=1 =0 Datos CAPt Dt Dt*CAPt 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 4. 20 5. 70 0 0 0 1 1 1 0 0 0 0 10. 5 11. 2 …. . . … …………………. . . ut …………………. . . Año Si t 7 4 otros 45

46 CAPt Dt 1 1 1 U = 0 + 1 CAP + 2 Dt*CAPt Dt．CAPt ……………………. … ut …………. … Año 79 80 81 82 83 84 85 86 87 88 89

La interpretacion de variables dummies en modelos de regresion Semilog (o Log-Lin) (Salario) (años de enseñanza) ln Y = 1 + 2 X + 3 D D 1 =0 hombre demas ln ^ Y = 2. 9298 + 0. 0546 X 2 + 0. 1341 D t=(481. 5) (48. 3) (27. 2) R 2 = 0. 995 dw = 2. 51 Tomando antilogaritmos de 0. 1341 = 1. 1435 Esto significa que el salario inicial de un profesor-hombre es mas alto que el de una profesora-mujer en un 14. 35 porciento. El modelo estimado para el salario de los profesoreshombres es: ^ ln Y = (2. 9298 + 0. 1341) + 0. 0546 X ^ ln Y = 3. 0639 + 0. 0546 X 47