1 Today Risk and Return Portfolio Theory Capital

1 Today Risk and Return • Portfolio Theory • Capital Asset Pricing Model Reading • Brealey, Myers, and Allen, Chapters 7 and 8

2 Measuring Risk • Variance - Average value of squared deviations from mean. A measure of volatility. • Standard Deviation - Average value of squared deviations from mean. A measure of volatility. • Variance measures ‘Total Risk’

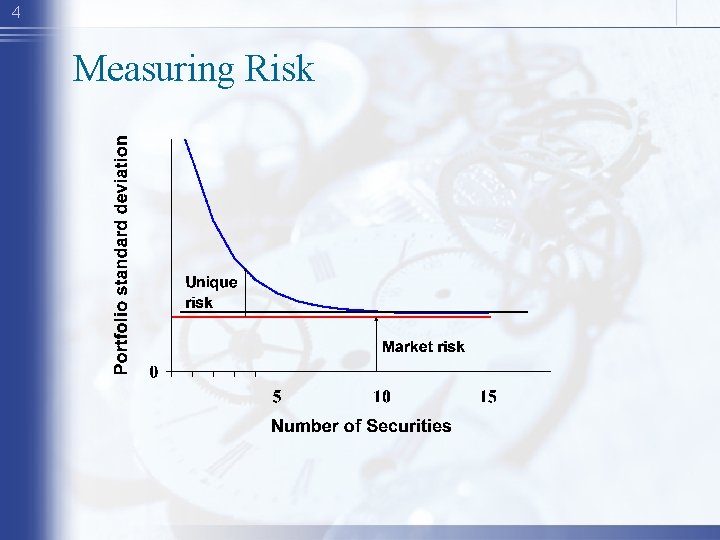
3 Measuring Risk • Unique Risk - Risk factors affecting only that firm. Also called “diversifiable risk. ” • Market Risk - Economy-wide sources of risk that affect the overall stock market. Also called “systematic risk. ” • Diversification - Strategy designed to reduce risk by spreading the portfolio across many investments.

4 Measuring Risk

5 Portfolio Risk The variance of a two stock portfolio is the sum of these four boxes

6 Portfolio Risk Example Suppose you invest 60% of your portfolio in Exxon Mobil and 40% in Coca Cola. The expected dollar return on your Exxon Mobil stock is 10% and on Coca Cola is 15%. The expected return on your portfolio is:

7 Portfolio Risk Example Suppose you invest 60% of your portfolio in Exxon Mobil and 40% in Coca Cola. The expected dollar return on your Exxon Mobil stock is 10% and on Coca Cola is 15%. The standard deviation of their annualized daily returns are 18. 2% and 27. 3%, respectively. Assume a correlation coefficient of 1. 0 and calculate the portfolio variance.

8 Portfolio Risk Example Suppose you invest 60% of your portfolio in Exxon Mobil and 40% in Coca Cola. The expected dollar return on your Exxon Mobil stock is 10% and on Coca Cola is 15%. The standard deviation of their annualized daily returns are 18. 2% and 27. 3%, respectively. Assume a correlation coefficient of 1. 0 and calculate the portfolio variance.

9 Portfolio Return and Risk

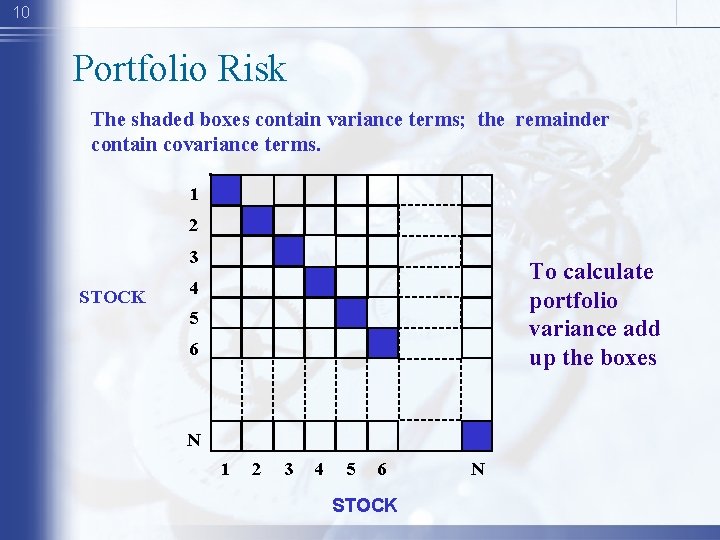
10 Portfolio Risk The shaded boxes contain variance terms; the remainder contain covariance terms. 1 2 3 STOCK To calculate portfolio variance add up the boxes 4 5 6 N 1 2 3 4 5 6 STOCK N

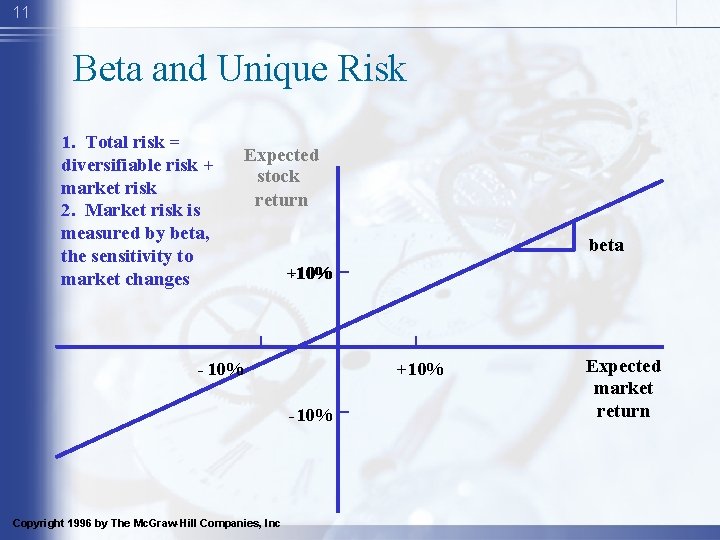
11 Beta and Unique Risk 1. Total risk = diversifiable risk + market risk 2. Market risk is measured by beta, the sensitivity to market changes Expected stock return beta +10% - 10% +10% -10% Copyright 1996 by The Mc. Graw-Hill Companies, Inc Expected market return

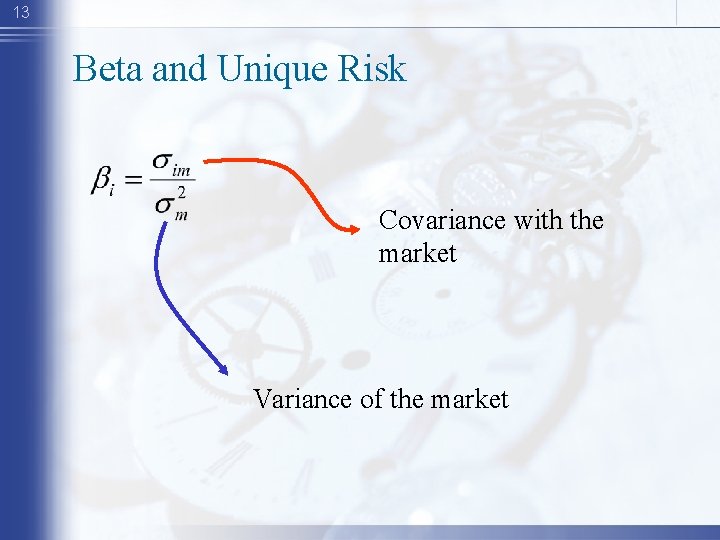
12 Beta and Unique Risk Market Portfolio - Portfolio of all assets in the economy. In practice a broad stock market index, such as the S&P Composite, is used to represent the market. Beta - Sensitivity of a stock’s return to the return on the market portfolio.

13 Beta and Unique Risk Covariance with the market Variance of the market

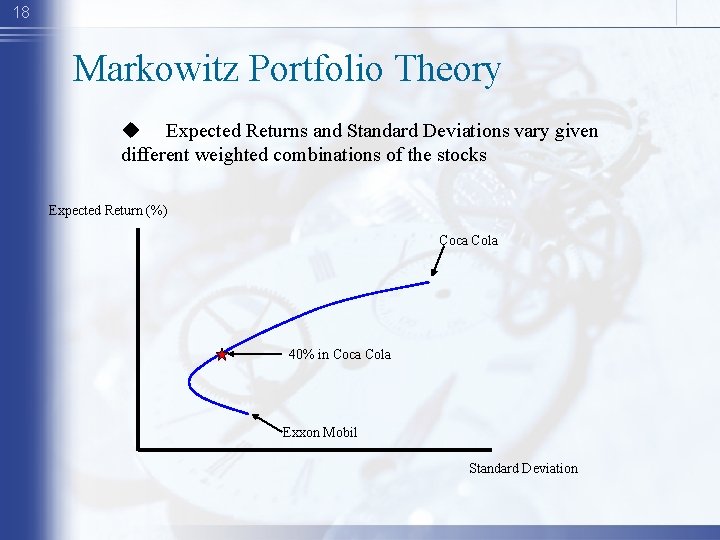
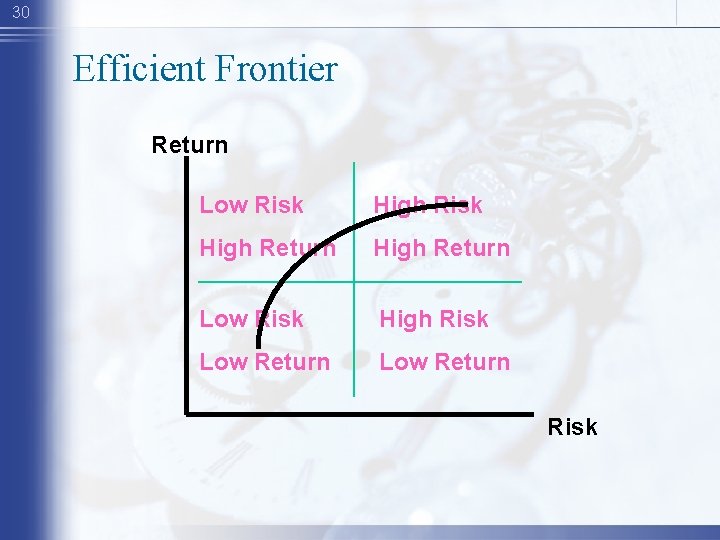
14 Markowitz Portfolio Theory • Combining stocks into portfolios can reduce standard deviation, below the level obtained from a simple weighted average calculation. • Correlation coefficients make this possible. • The various weighted combinations of stocks that create this standard deviations constitute the set of efficient portfolios

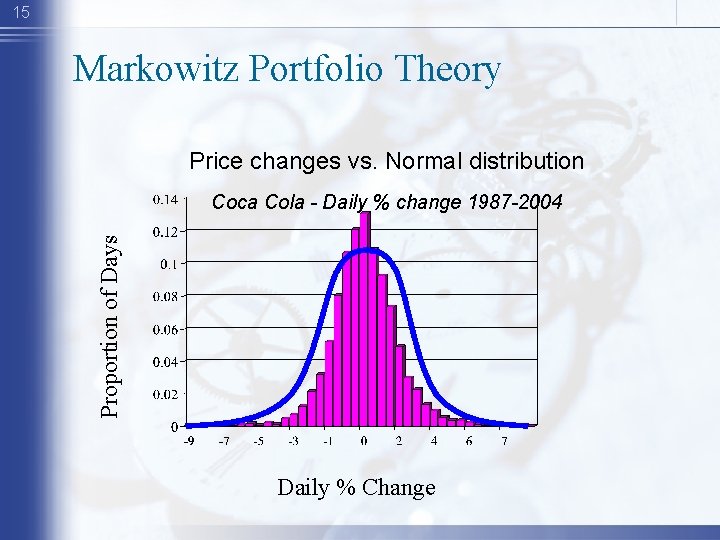
15 Markowitz Portfolio Theory Price changes vs. Normal distribution Proportion of Days Coca Cola - Daily % change 1987 -2004 Daily % Change

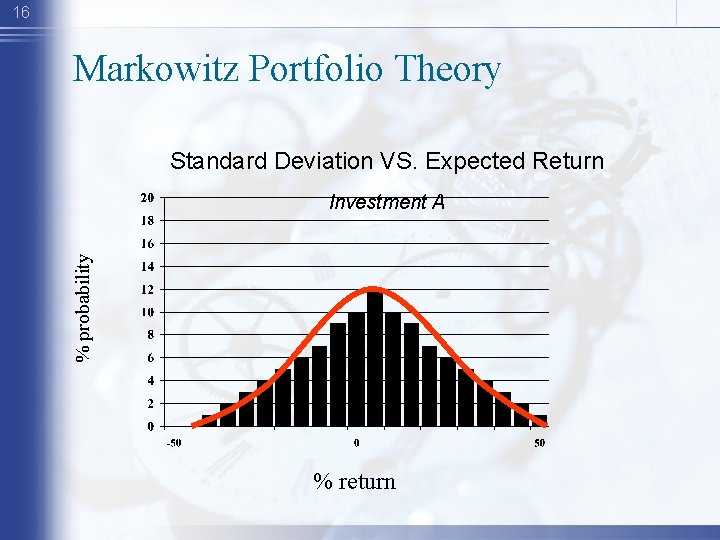
16 Markowitz Portfolio Theory Standard Deviation VS. Expected Return % probability Investment A % return

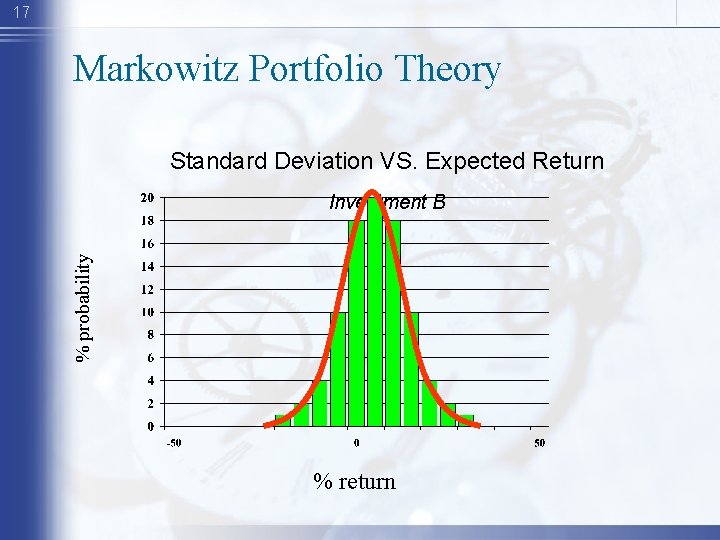
17 Markowitz Portfolio Theory Standard Deviation VS. Expected Return % probability Investment B % return

18 Markowitz Portfolio Theory u Expected Returns and Standard Deviations vary given different weighted combinations of the stocks Expected Return (%) Coca Cola 40% in Coca Cola Exxon Mobil Standard Deviation

19 Efficient Frontier • Each half egg shell represents the possible weighted combinations for two stocks. • The composite of all stock sets constitutes the efficient frontier Expected Return (%) Standard Deviation

20 Efficient Frontier • Lending or Borrowing at the risk free rate (rf) allows us to exist outside the efficient frontier. Expected Return (%) T ing w rro Bo g in nd e L rf S Standard Deviation

21 Efficient Frontier Example Stocks ABC Corp Big Corp s 28 42 Correlation Coefficient =. 4 % of Portfolio Avg Return 60% 15% 40% 21% Standard Deviation = weighted avg = Standard Deviation = Portfolio = Return = weighted avg = Portfolio =

22 Efficient Frontier Example Stocks ABC Corp Big Corp s 28 42 Correlation Coefficient =. 4 % of Portfolio Avg Return 60% 15% 40% 21% Standard Deviation = weighted avg = Standard Deviation = Portfolio = Return = weighted avg = Portfolio = Let’s Add stock New Corp to the portfolio

23 Efficient Frontier Example Stocks Portfolio New Corp s 28. 1 30 Correlation Coefficient =. 3 % of Portfolio Avg Return 50% 17. 4% 50% 19% NEW Standard Deviation = weighted avg = NEW Standard Deviation = Portfolio = NEW Return = weighted avg = Portfolio = NOTE: Higher return & Lower risk How did we do that? DIVERSIFICATION

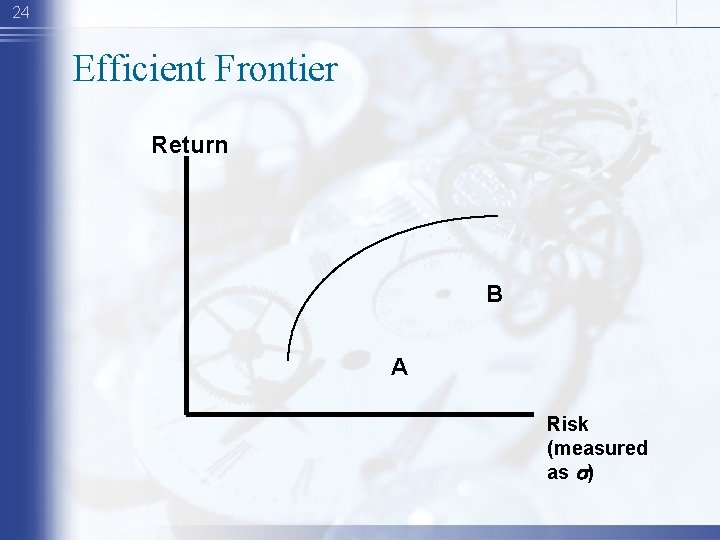
24 Efficient Frontier Return B A Risk (measured as s)

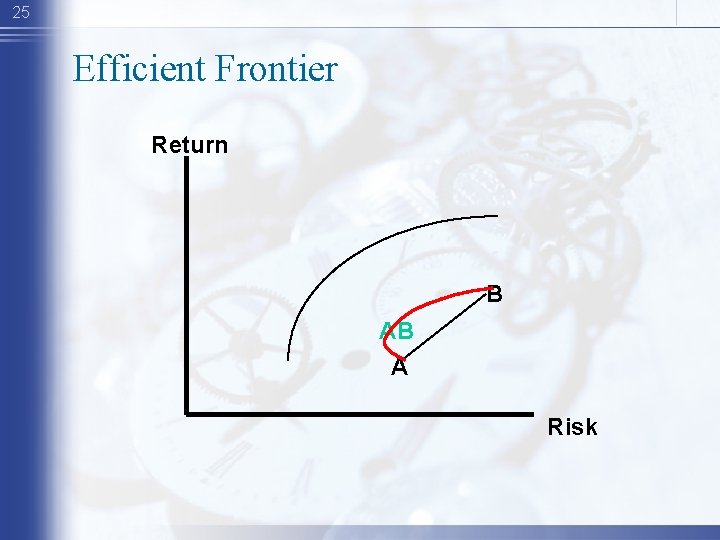
25 Efficient Frontier Return B AB A Risk

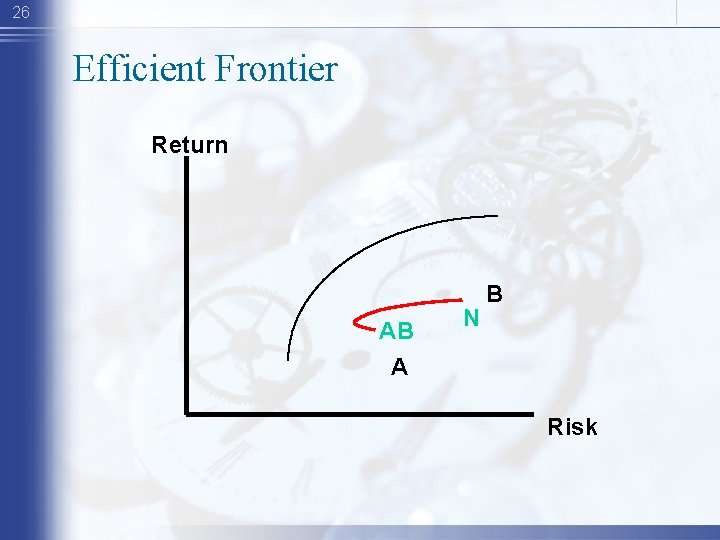
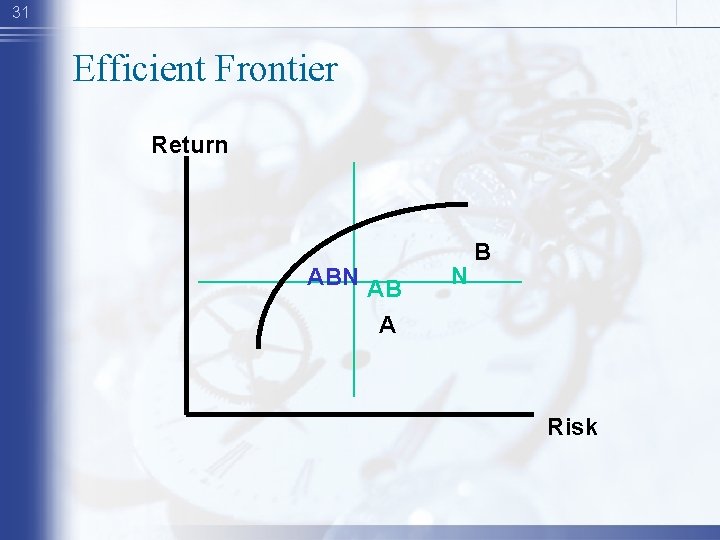
26 Efficient Frontier Return AB A N B Risk

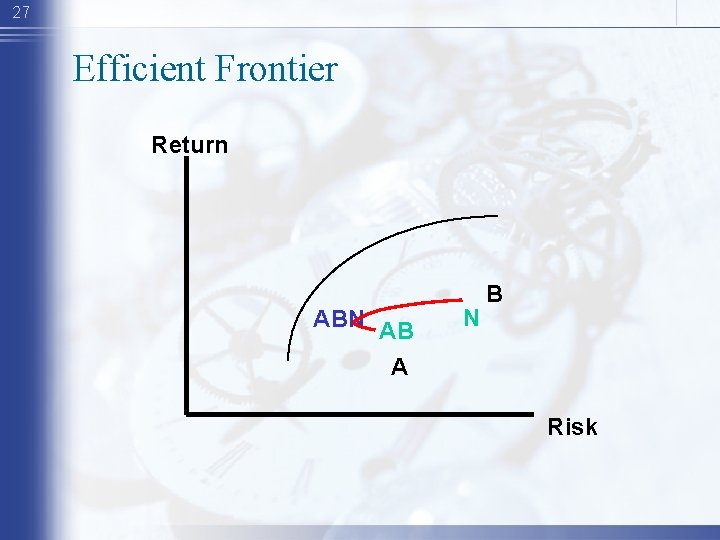
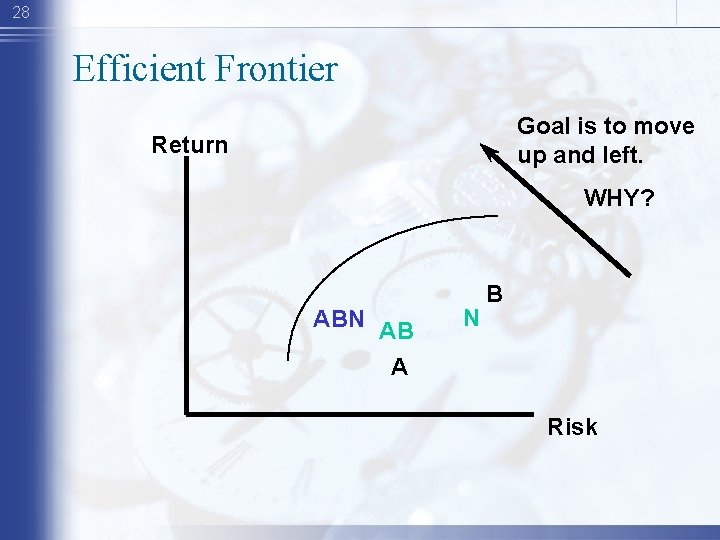
27 Efficient Frontier Return ABN AB A N B Risk

28 Efficient Frontier Goal is to move up and left. Return WHY? ABN AB A N B Risk

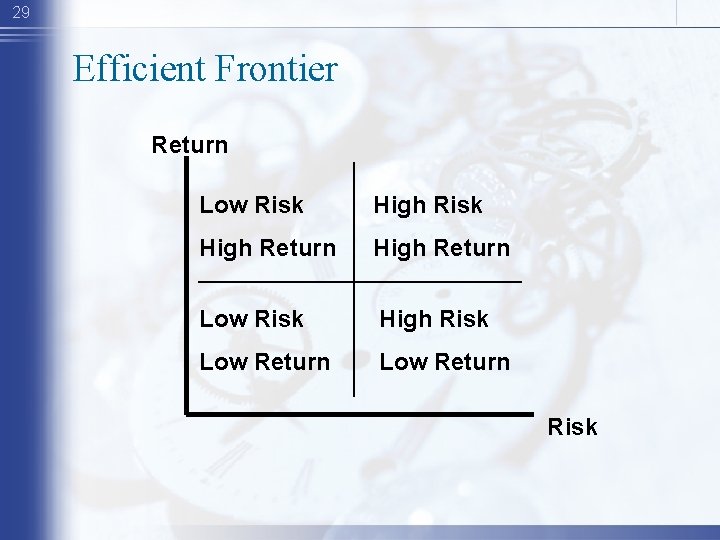
29 Efficient Frontier Return Low Risk High Return Low Risk High Risk Low Return Risk

30 Efficient Frontier Return Low Risk High Return Low Risk High Risk Low Return Risk

31 Efficient Frontier Return ABN AB A N B Risk

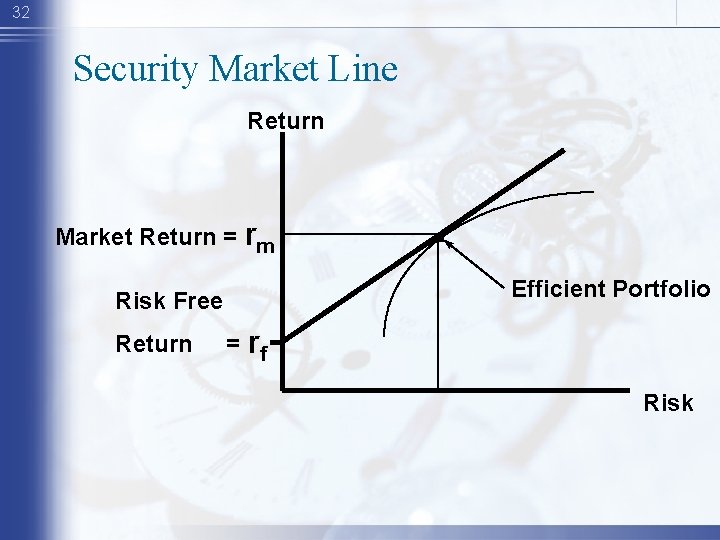
32 Security Market Line Return Market Return = rm Efficient Portfolio Risk Free Return . = rf Risk

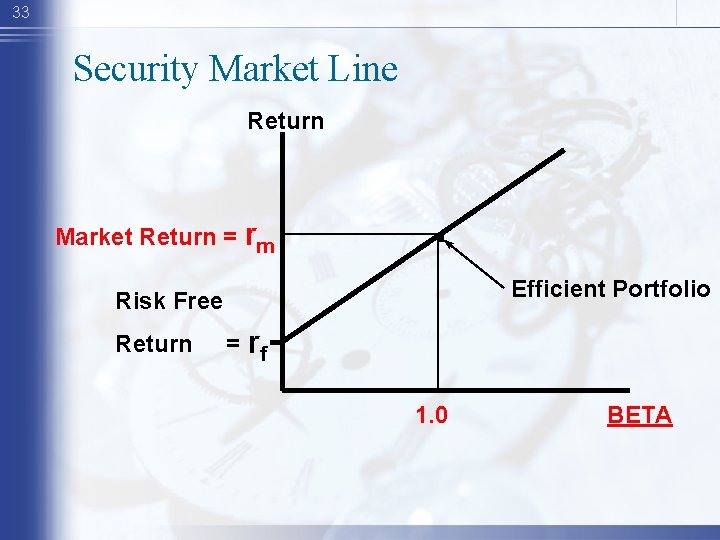
33 Security Market Line Return Market Return = rm . Efficient Portfolio Risk Free Return = rf 1. 0 BETA

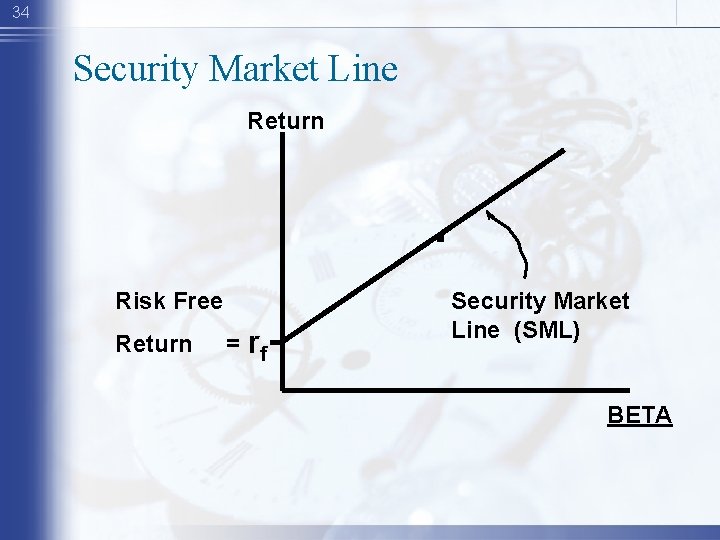
34 Security Market Line Return . Risk Free Return = rf Security Market Line (SML) BETA

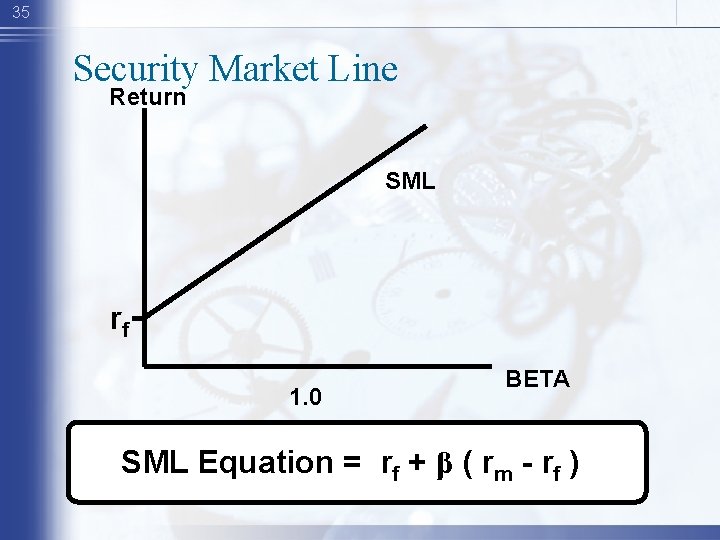
35 Security Market Line Return SML rf 1. 0 BETA SML Equation = rf + β ( rm - rf )

36 Capital Asset Pricing Model R = r f + β ( rm - rf ) CAPM

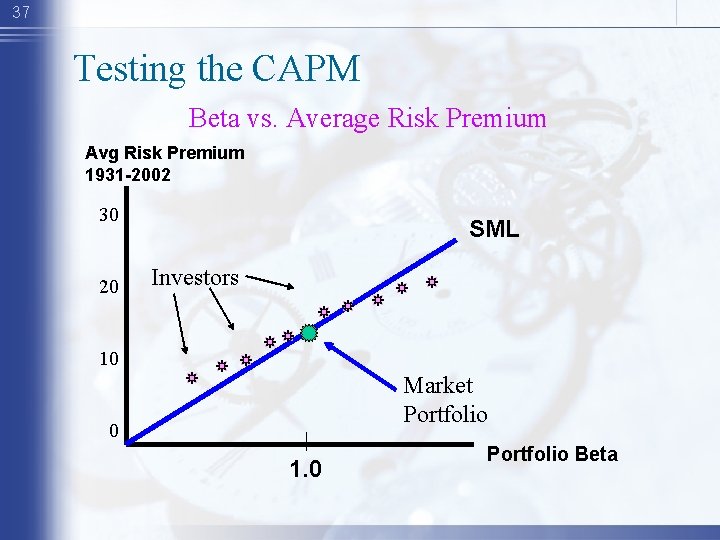
37 Testing the CAPM Beta vs. Average Risk Premium Avg Risk Premium 1931 -2002 30 20 SML Investors 10 Market Portfolio 0 1. 0 Portfolio Beta

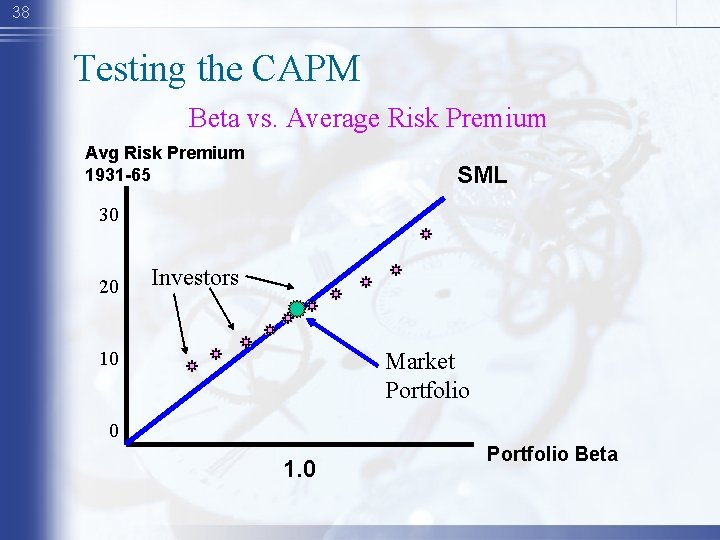
38 Testing the CAPM Beta vs. Average Risk Premium Avg Risk Premium 1931 -65 SML 30 20 Investors 10 Market Portfolio 0 1. 0 Portfolio Beta

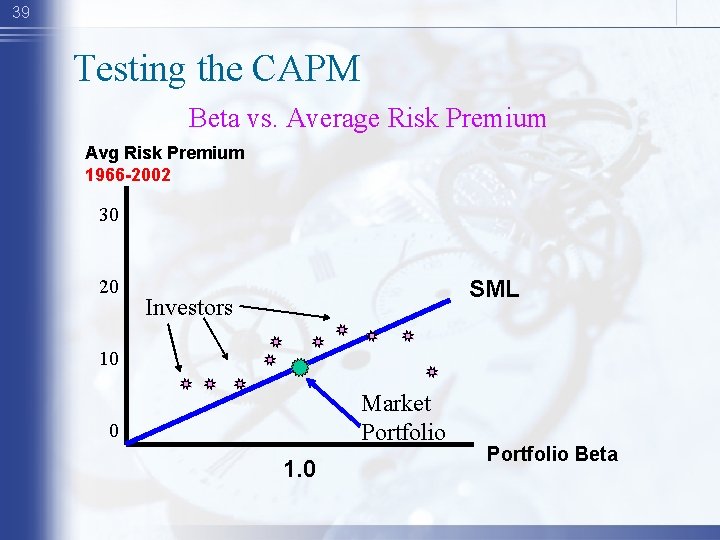
39 Testing the CAPM Beta vs. Average Risk Premium Avg Risk Premium 1966 -2002 30 20 SML Investors 10 Market Portfolio 0 1. 0 Portfolio Beta

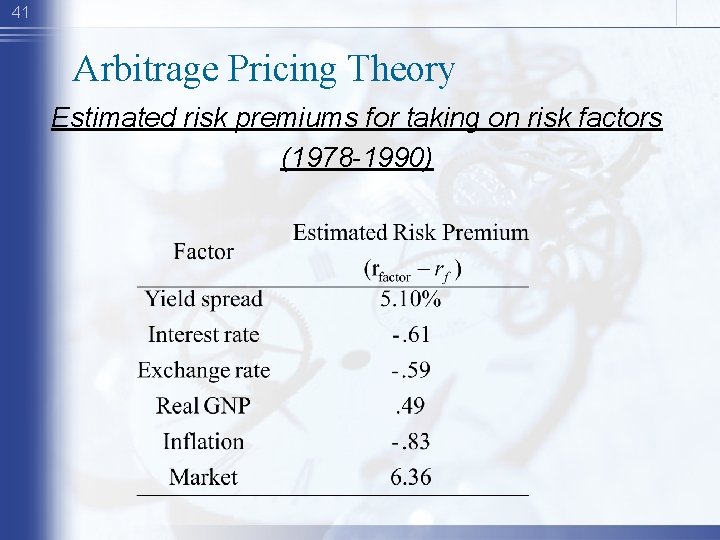
40 Arbitrage Pricing Theory Alternative to CAPM Expected Risk Premium = r - rf = Bfactor 1(rfactor 1 - rf) + Bf 2(rf 2 - rf) + … Return = a + bfactor 1(rfactor 1) + bf 2(rf 2) + …

41 Arbitrage Pricing Theory Estimated risk premiums for taking on risk factors (1978 -1990)