1 Throughput maximization by improved bottleneck control Elvira

1 Throughput maximization by improved bottleneck control Elvira Marie B. Aske*&, Sigurd Skogestad* and Stig Strand& *Department of Chemical Engineering, Norwegian University of Science and Technology, Trondheim, Norway &Statoil R&D, Process Control, Trondheim, Norway

2 Outline • • • Modes of optimal operation Maximum throughput Throughput manipulator (TPM) Max-flow min-cut theorem Realizing maximum throughput – Single-loop – MPC • Back off • Conclusions

3 Depending on marked conditions: Two main modes of optimal operation Mode 1. Given throughput (“nominal case”) Given feed or product rate “Maximize efficiency”: Unconstrained optimum (“trade-off”) Mode 2. Max/Optimum throughput Throughput is a degree of freedom + good product prices 2 a) Maximum throughput Increase throughput until constraints give infeasible operation Constrained optimum - identify active constraints (bottleneck!) 2 b) Optimized throughput Increase throughput until further increase is uneconomical Unconstrained optimum

4 Mode 2 a: Maximum throughput • Typical profit function: • Feed flows are set in proportion to F and assume constant efficiencies: • Leads to: Maximize profit → Maximize throughput F

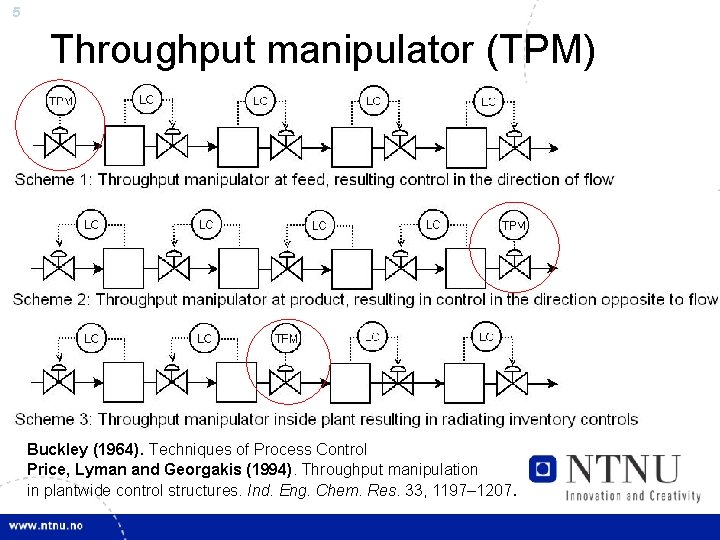
5 Throughput manipulator (TPM) Buckley (1964). Techniques of Process Control Price, Lyman and Georgakis (1994). Throughput manipulation in plantwide control structures. Ind. Eng. Chem. Res. 33, 1197– 1207.

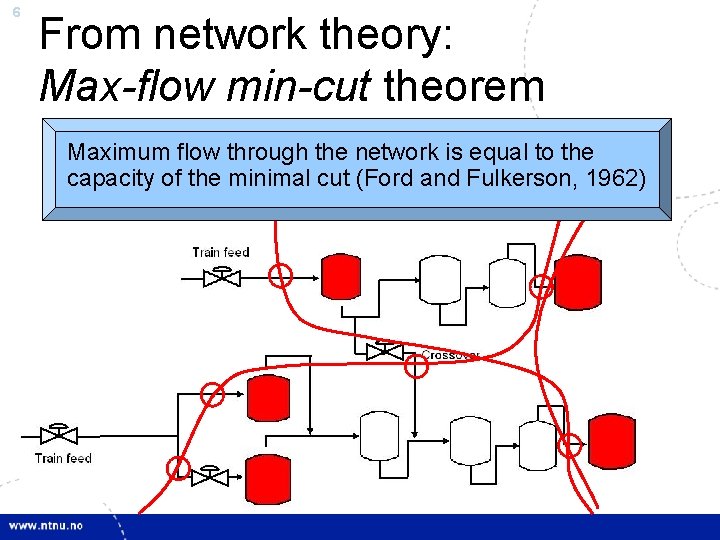
6 From network theory: Max-flow min-cut theorem Maximum flow through the network is equal to the capacity of the minimal cut (Ford and Fulkerson, 1962)

7 Bottleneck • Maximum throughput achieved by maximizing the flow through the bottleneck • If the flow for some time is not at its maximum through the bottleneck, then this loss can never be recovered Maximum throughput requires tight control of the bottleneck unit

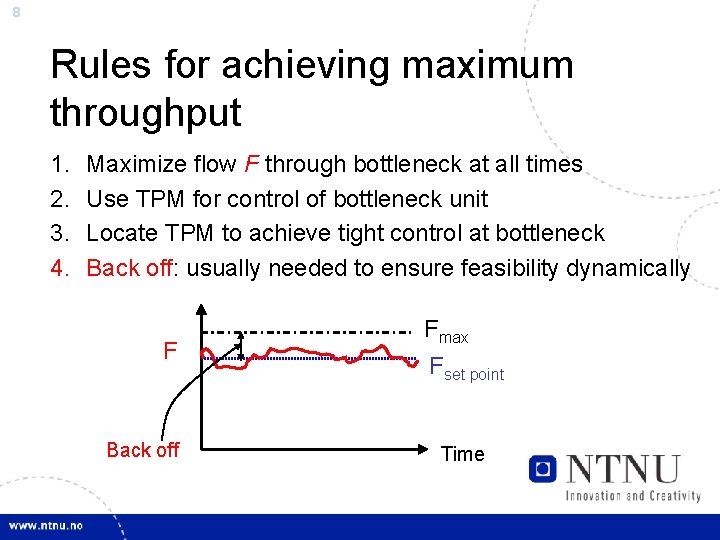
8 Rules for achieving maximum throughput 1. 2. 3. 4. Maximize flow F through bottleneck at all times Use TPM for control of bottleneck unit Locate TPM to achieve tight control at bottleneck Back off: usually needed to ensure feasibility dynamically F Back off Fmax Fset point Time

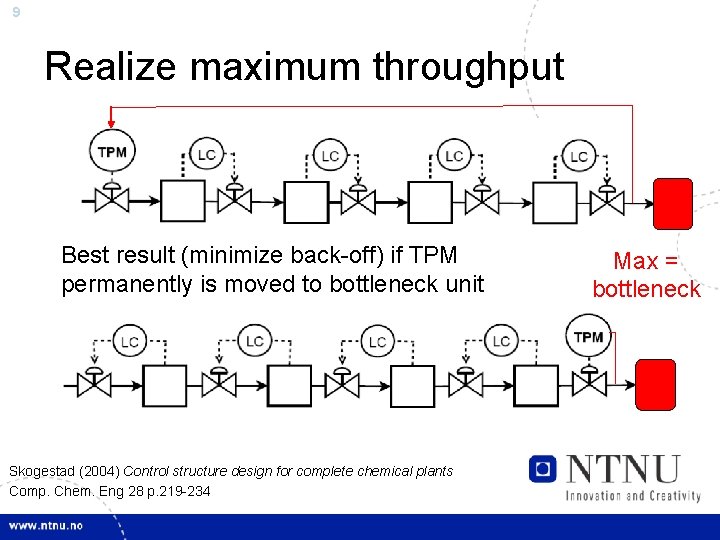
9 Realize maximum throughput Best result (minimize back-off) if TPM permanently is moved to bottleneck unit Skogestad (2004) Control structure design for complete chemical plants Comp. Chem. Eng 28 p. 219 -234 Max = bottleneck

10 Realize maximum throughput in more complex cases • Bottleneck moves • Multiple feeds and crossovers Proposed solution: Coordinator MPC* - Estimate of remaining capacity in each unit is obtained from local MPCs - Coordinator MPC manipulate TPMs (+ crossovers) to maximize flow through bottlenecks *Aske et al. (2007) Coordinator MPC for maximizing plant throughput Submitted to Comp. Chem. Eng

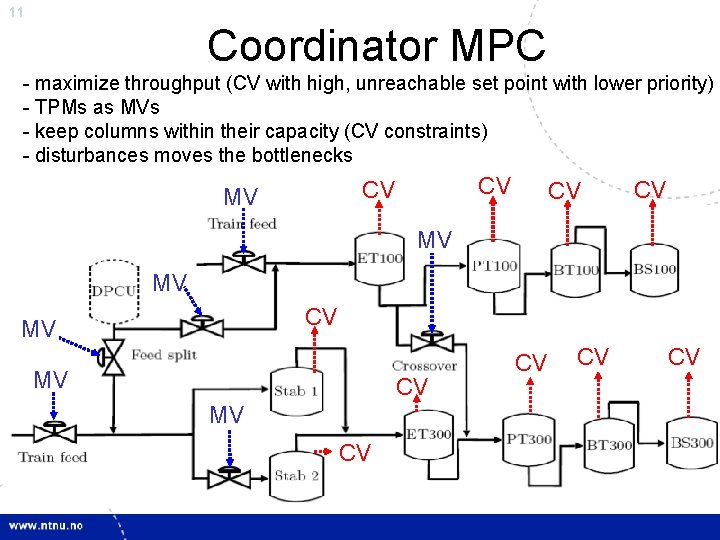
11 Coordinator MPC - maximize throughput (CV with high, unreachable set point with lower priority) - TPMs as MVs - keep columns within their capacity (CV constraints) - disturbances moves the bottlenecks CV CV MV MV CV CV

12 Back off = loss (in throughput) • Back off can be reduced by – Improved control (to some extent) • Limited by network dynamics from TPM to bottleneck – Obtain TPM closer to bottleneck • Move TPM (Change in base control) • Add buffer tanks to get dynamic TPMs (Design change) or use existing buffer volumes • Estimate back off to find economic incentive: • Worst case amplification:

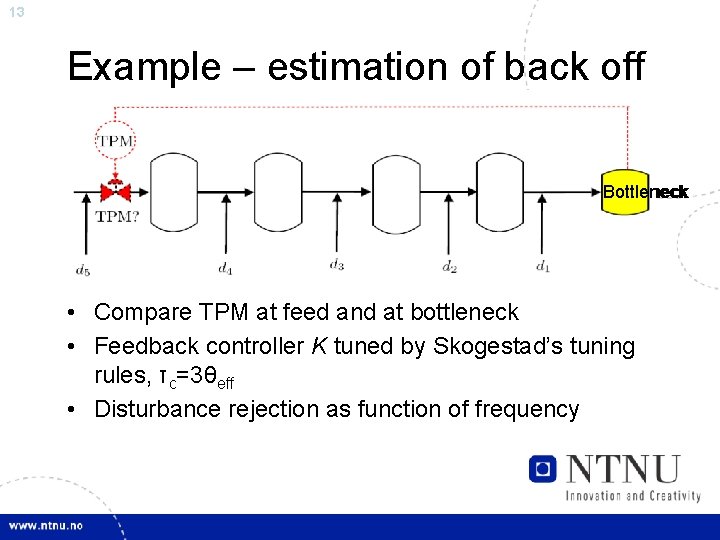
13 Example – estimation of back off Bottleneck • Compare TPM at feed and at bottleneck • Feedback controller K tuned by Skogestad’s tuning rules, τc=3θeff • Disturbance rejection as function of frequency

14 Back off as a function of frequency • Peak unavoidable • Effect of disturbances reduced

15 Conclusions • Tighter bottleneck control can reduce back off • TPM should be used for control of the bottleneck unit to obtain maximum flow • Bottleneck fixed →single-loop control sufficient • Bottleneck moves → multivariable control • Consider moving/adding TPM if back off is large