1 The Term Structure of Interest Rates Chapter

2 Term Structure of Interest Rates Definition: For securities of equal risk, it shows

3 The Term Structure Identifying the Existing Term Structure Use ◦ ◦ ◦ spot

4 Yield Curve Shapes Yield Upward sloping or normal Short-term yields are smaller than

5 Yield Curves and the Business Cycle Downward sloping yield curve often appears at

6 The Term Structure and the General Level of Interest Rates When the general

7 Four Theories Unbiased (Pure) Expectations Theory Liquidity Preference Theory Segmented Markets Theory Preferred

8 Unbiased (Pure) Expectations Theory Oberservable Long-Term yields are the average of expected, but

9 Unbiased (Pure) Expectations Theory Mathematics of the Pure Expectations Theory 1+ 1 rn

10 Table 9. 1 OBSERVED AND EXPECTED ONE-YEAR YIELDS AND PREMIUMS AS OF JANUARY

11 What is the yield to maturity on a four -year Treasury security bought

12 What are the spot yields on securities with two-and three-year maturities as of

13 Strategy: Buy a two-year security in January 2005 (annual yield of 8. 999%)

14 Strategy: Buy a three-year security in January 2005 (annual yield of 9. 662%)

15 Conclusion from the Examples As shown, if the pure expectation theory is correct,

16 Figure 9. 9 Hypothetical Observed Yield Curve, January 2005 Because long-term yields are

17 An Example Today’s newspaper indicates that the rate on a one-year U. S.

18 Incorporating Liquidity Premiums If it is believed that investors expect a liquidity premium

19 Using Data from Table 9. 1 Hypothetical Example: Liquidity Preference 1 + 1

20 Figure 9. 12 Hypothetical Observed Yield Curve with Liquidity Premium If short-term rates

21 Other Theories The Liquidity Premium Hypothesis (Theory) • • Long-term securities are riskier

22 Other Theories (continued) The Segmented Markets Theory • • • There is not

23 Empirical Tests of the Term Structure Theories Measuring Expectations Evidence on Liquidity Premiums

24 Interest Rate Forecasting Using the yield curve to forecast forward rates Based on

25 Setting Institutional Interest Rates Estimating deposit rates and setting the mortgage rate Using

26 Table 9. 3 USING THE TERM STRUCTURE TO SET INSTITUTIONAL INTEREST RATES The

27 Table 9. 3 ESTIMATED REQUIRED ESTIMATED PREMIUM ANNUAL RETURN (INLUDING A PROFIT MARKUP

28 Setting Loan Credit Risk Premiums Requires the calculation of the: • • •

29 Managing the Securities Portfolio The Market Are Sometimes in Temporary Disequilibrium. • •

Slides: 29

Download presentation

2 Term Structure of Interest Rates Definition: For securities of equal risk, it shows the relationship between the yield and various maturities. When graphed, it is called the yield curve. Securities must be of equal risk and with all other characteristics identical except maturity. Yield curve is generated from actual market data and thus reflects the behavior of multiple participants in the market. Yield curve reveals the market participants’ expectations of future interest rates. Copyright © 2004 by Thomson Southwestern All rights reserved.

3 The Term Structure Identifying the Existing Term Structure Use ◦ ◦ ◦ spot rates on securities of equal risk Treasury Bills (T-Bills) Treasury Notes Treasury Bonds Graphing the data • • Yield on the vertical axis Maturity on the horizontal axis Different shapes result • • • “Normal” (upward-sloping) Downward-sloping Flat Copyright © 2004 by Thomson Southwestern All rights reserved.

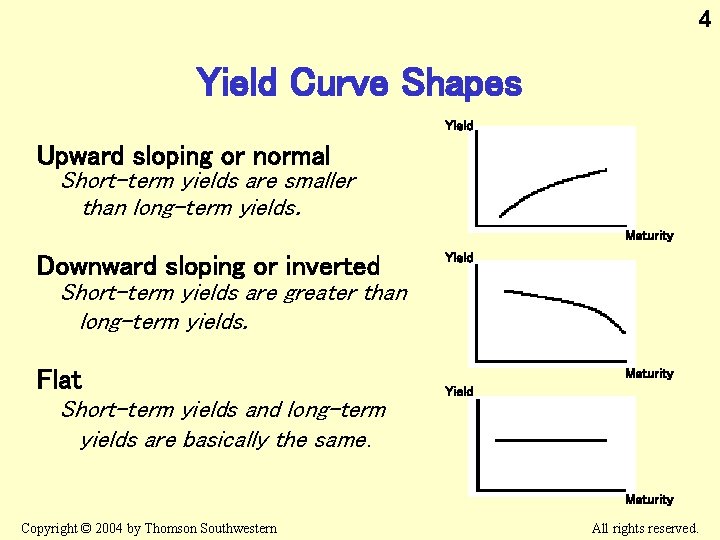
4 Yield Curve Shapes Yield Upward sloping or normal Short-term yields are smaller than long-term yields. Maturity Downward sloping or inverted Yield Short-term yields are greater than long-term yields. Flat Short-term yields and long-term yields are basically the same. Maturity Yield Maturity Copyright © 2004 by Thomson Southwestern All rights reserved.

5 Yield Curves and the Business Cycle Downward sloping yield curve often appears at the peak of the business cycle. • Investors seem to anticipate recession with the lower demand for funds and a decrease in interest rates. During sluggish economic performance but towards the end of a recession, the yield curve has often been upward sloping. • Investors anticipate the end of a recession and an increase in future rates. Copyright © 2004 by Thomson Southwestern All rights reserved.

6 The Term Structure and the General Level of Interest Rates When the general level of interest rate is relatively high, yield curves are usually downward-sloping. When the general level of interest rate is relatively low, the yield curve often slopes upward. Copyright © 2004 by Thomson Southwestern All rights reserved.

8 Unbiased (Pure) Expectations Theory Oberservable Long-Term yields are the average of expected, but directly unobservable, short-term yields. Assumptions of the Pure Expectations Theory • • All else equal, investors are indifferent between owning a single long-term security or a series of short-term securities over the same time period. In other words, maturity alone does not affect investors’ choice of investments All Investors hold common expectations about the course of shortterm rates On average, investors are able to predict rates accurately. Their expectations about future rates are unbiased in the statistical sense, that are neither consistently low nor consistently high. There are no taxes, information costs, or transaction costs in the financial markets. Investors are free to exchange securities of varying maturities quickly and without penalty. Copyright © 2004 by Thomson Southwestern All rights reserved.

9 Unbiased (Pure) Expectations Theory Mathematics of the Pure Expectations Theory 1+ 1 rn = [(1 + 1 r 1 ) (1 + 2 c 1 ) …(1 + n c 1 )1/n ] The observed yield in period 1 of a security with n years to maturity is (1 rn) 2 c 1 is the expected yield of a one-year security at the beginning of period 2 1 rn is the geometric average of a series of one-year current and expected yields over this period Copyright © 2004 by Thomson Southwestern All rights reserved.

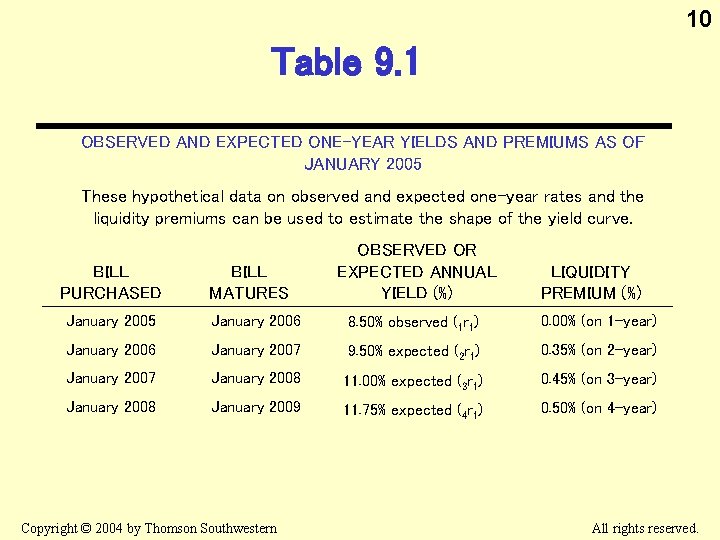
10 Table 9. 1 OBSERVED AND EXPECTED ONE-YEAR YIELDS AND PREMIUMS AS OF JANUARY 2005 These hypothetical data on observed and expected one-year rates and the liquidity premiums can be used to estimate the shape of the yield curve. BILL PURCHASED BILL MATURES OBSERVED OR EXPECTED ANNUAL YIELD (%) LIQUIDITY PREMIUM (%) January 2005 January 2006 8. 50% observed (1 r 1) 0. 00% (on 1 -year) January 2006 January 2007 9. 50% expected (2 r 1) 0. 35% (on 2 -year) January 2007 January 2008 11. 00% expected (3 r 1) 0. 45% (on 3 -year) January 2008 January 2009 11. 75% expected (4 r 1) 0. 50% (on 4 -year) Copyright © 2004 by Thomson Southwestern All rights reserved.

13 Strategy: Buy a two-year security in January 2005 (annual yield of 8. 999%) and two successive one-year T-bills in 2007 and 2008 with 11% and 11. 75% yields, respectively. What is the holding period return? 1 + i. H = [(1. 08999)(1. 1100)(1. 1175)](1/4) i. H = 1. 10180 -1 =. 1018 or 10. 18% Copyright © 2004 by Thomson Southwestern All rights reserved.

14 Strategy: Buy a three-year security in January 2005 (annual yield of 9. 662%) and a one-year T-bill in 2008 with a 11. 75% yield. What is the holding period return? 1 + i. H = [(1. 09662)(1. 09962)(1. 1175)](1/4) i. H = 1. 10180 -1 =. 1018 or 10. 18% Copyright © 2004 by Thomson Southwestern All rights reserved.

15 Conclusion from the Examples As shown, if the pure expectation theory is correct, the average annual yield an investor could obtain over the period 2005 -2009 is the same, regardless of the investment strategy chosen. This will be true as long as: all proceeds are reinvested; and q expectations about future rates remain constant during the period. q Copyright © 2004 by Thomson Southwestern All rights reserved.

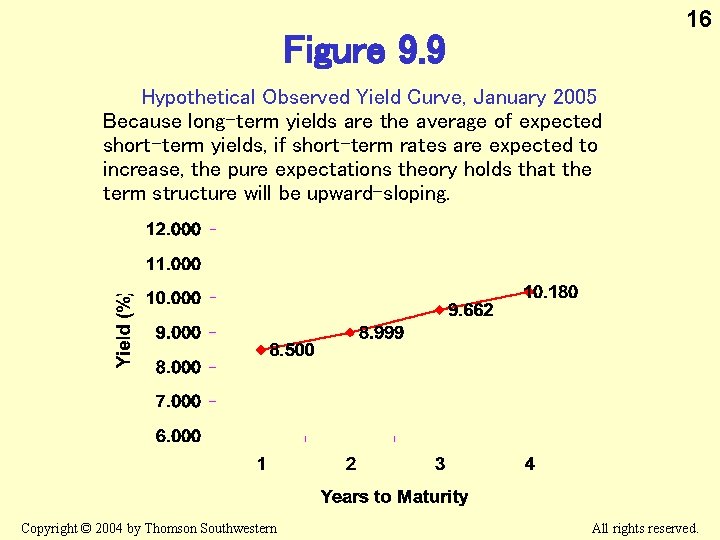
16 Figure 9. 9 Hypothetical Observed Yield Curve, January 2005 Because long-term yields are the average of expected short-term yields, if short-term rates are expected to increase, the pure expectations theory holds that the term structure will be upward-sloping. Copyright © 2004 by Thomson Southwestern All rights reserved.

17 An Example Today’s newspaper indicates that the rate on a one-year U. S. Treasury security is 1. 97% and the rate on a two-year U. S. Treasury security is 2. 86%. What does the market expect the rate to be on a one-year U. S. Treasury security beginning one year from today? 2 c = [(1 + r ) 2 1 1 2 /(1 + 1 r 1 ) ] - 1 2 c = [(1 +. 0286) /(1 +. 0197 ) ] - 1 2 1 2 c 1 = 1. 0376 – 1 =. 0376 = 3. 76% Copyright © 2004 by Thomson Southwestern All rights reserved.

18 Incorporating Liquidity Premiums If it is believed that investors expect a liquidity premium of 0. 25 percent, then 1 + 1 r 2 =[(1 + 1 r 1 ) (1 + 2 c 1 + L 2) ]1/2 where L 2 is the liquidity premium for holding a two-year security, then using the previous example, 2 c = [(1 + r ) 2 1 1 2 /(1 + 1 r 1 ) ] – 1 - L 2 2 c = [(1 +. 0286) /(1 +. 0197 ) ] – 1 -. 0025 2 1 2 c 1 = 1. 0376 – 1 -. 0025 =. 0376 -. 0025 = 3. 51% Copyright © 2004 by Thomson Southwestern All rights reserved.

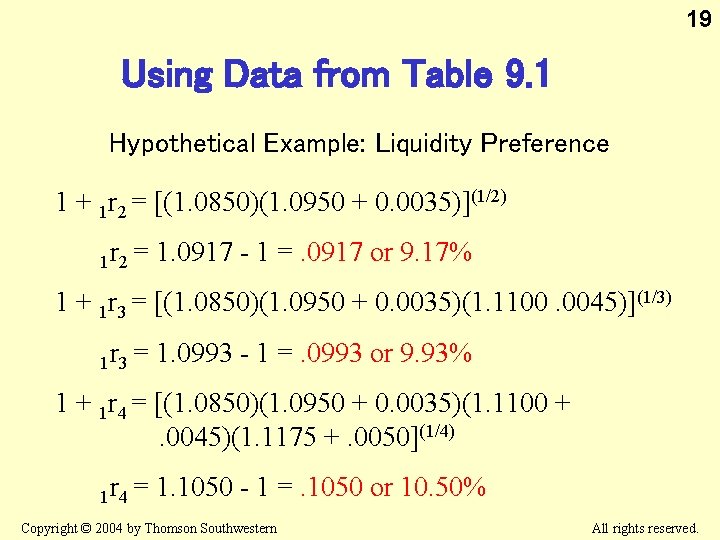
19 Using Data from Table 9. 1 Hypothetical Example: Liquidity Preference 1 + 1 r 2 = [(1. 0850)(1. 0950 + 0. 0035)](1/2) 1 r 2 = 1. 0917 - 1 =. 0917 or 9. 17% 1 + 1 r 3 = [(1. 0850)(1. 0950 + 0. 0035)(1. 1100. 0045)](1/3) 1 r 3 = 1. 0993 - 1 =. 0993 or 9. 93% 1 + 1 r 4 = [(1. 0850)(1. 0950 + 0. 0035)(1. 1100 +. 0045)(1. 1175 +. 0050](1/4) 1 r 4 = 1. 1050 - 1 =. 1050 or 10. 50% Copyright © 2004 by Thomson Southwestern All rights reserved.

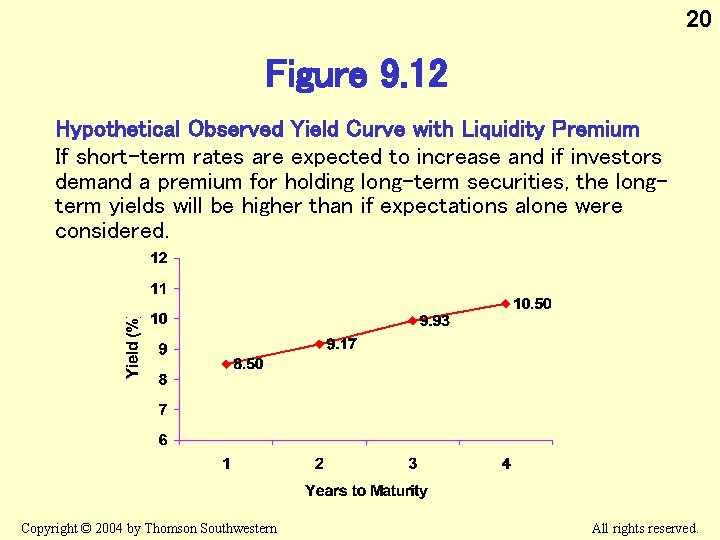
20 Figure 9. 12 Hypothetical Observed Yield Curve with Liquidity Premium If short-term rates are expected to increase and if investors demand a premium for holding long-term securities, the longterm yields will be higher than if expectations alone were considered. Copyright © 2004 by Thomson Southwestern All rights reserved.

21 Other Theories The Liquidity Premium Hypothesis (Theory) • • Long-term securities are riskier than short-term securities Over time, investors will have more and more other opportunities/needs for funds and thus demand a term premium to hold longer term securities The Modified Expectations Theory • • • Expectation of future rates determine today’s yields Expectation of rising rates leads to normal curve Expectation of falling rates leads to downward-sloping curve Copyright © 2004 by Thomson Southwestern All rights reserved.

22 Other Theories (continued) The Segmented Markets Theory • • • There is not one market and no term structure Different investors and borrowers are in each maturity market Supply and demand determine the interest rate separately for each maturity of securities The Preferred Habitat Theory • • Investors prefer particular segments of the market but they will move to others given sufficient inducement Supply and demand imbalances in various markets provide premiums for inducement Copyright © 2004 by Thomson Southwestern All rights reserved.

23 Empirical Tests of the Term Structure Theories Measuring Expectations Evidence on Liquidity Premiums Research on Segmented Markets and Preferred Habitats Copyright © 2004 by Thomson Southwestern All rights reserved.

24 Interest Rate Forecasting Using the yield curve to forecast forward rates Based on pure expectations theory • Investor is indifferent to owning one security or a series of securities over the investment horizon, or 1 + 1 r 2 =[(1 + 1 r 1 ) (1 + 2 c 1 ) ]1/2 • Where 2 c 1 is unobservable expected one-year rate at the beginning of period 2 • Forward rate is an implied expected rate 2 or c = [(1 + r ) 2 1 1 2 /(1 + 1 r 1 ) ] - 1 Copyright © 2004 by Thomson Southwestern All rights reserved.

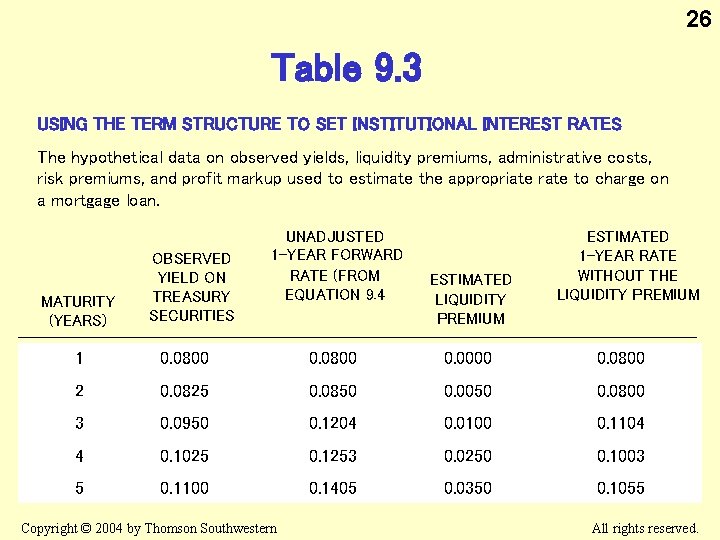
25 Setting Institutional Interest Rates Estimating deposit rates and setting the mortgage rate Using observed yield on Treasury securities, Calculate one-year forward rates for each year, Less estimated liquidity premium, Equals estimated deposit rates Plus Equals administrative cost of deposits premium required to hold mortgages annual required return estimated mortgage rate Copyright © 2004 by Thomson Southwestern All rights reserved.

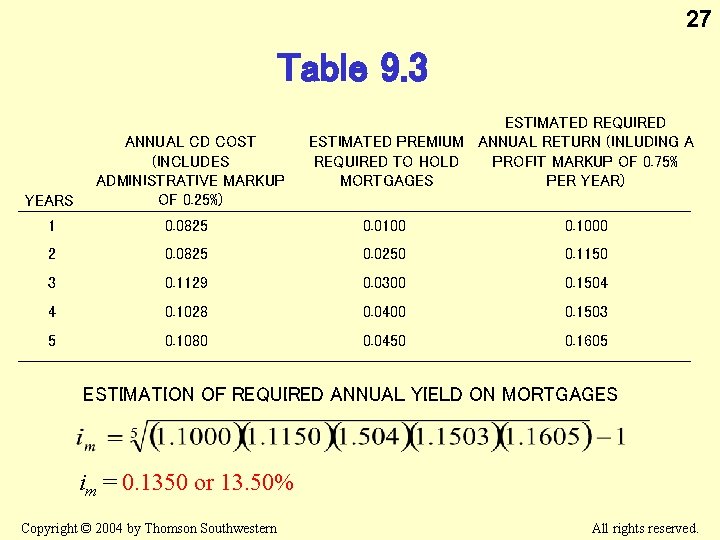
26 Table 9. 3 USING THE TERM STRUCTURE TO SET INSTITUTIONAL INTEREST RATES The hypothetical data on observed yields, liquidity premiums, administrative costs, risk premiums, and profit markup used to estimate the appropriate rate to charge on a mortgage loan. MATURITY (YEARS) OBSERVED YIELD ON TREASURY SECURITIES UNADJUSTED 1 -YEAR FORWARD RATE (FROM EQUATION 9. 4 ESTIMATED LIQUIDITY PREMIUM ESTIMATED 1 -YEAR RATE WITHOUT THE LIQUIDITY PREMIUM 1 0. 0800 0. 0000 0. 0800 2 0. 0825 0. 0850 0. 0050 0. 0800 3 0. 0950 0. 1204 0. 0100 0. 1104 4 0. 1025 0. 1253 0. 0250 0. 1003 5 0. 1100 0. 1405 0. 0350 0. 1055 Copyright © 2004 by Thomson Southwestern All rights reserved.

27 Table 9. 3 ESTIMATED REQUIRED ESTIMATED PREMIUM ANNUAL RETURN (INLUDING A PROFIT MARKUP OF 0. 75% REQUIRED TO HOLD PER YEAR) MORTGAGES YEARS ANNUAL CD COST (INCLUDES ADMINISTRATIVE MARKUP OF 0. 25%) 1 0. 0825 0. 0100 0. 1000 2 0. 0825 0. 0250 0. 1150 3 0. 1129 0. 0300 0. 1504 4 0. 1028 0. 0400 0. 1503 5 0. 1080 0. 0450 0. 1605 ESTIMATION OF REQUIRED ANNUAL YIELD ON MORTGAGES im = 0. 1350 or 13. 50% Copyright © 2004 by Thomson Southwestern All rights reserved.

28 Setting Loan Credit Risk Premiums Requires the calculation of the: • • • forward rate for next year’s one-year Treasury bond forward rate for next year’s corporate bond with the desired credit risk classification The risk premium (for that credit risk classification) is the difference in the forward rates The probability of no default for the corporate bond is calculated by taking the ratio of (1 + forward rate for treasuries) to (1+ forward rate for the corporate bond). Copyright © 2004 by Thomson Southwestern All rights reserved.

29 Managing the Securities Portfolio The Market Are Sometimes in Temporary Disequilibrium. • • If a security’s yield is higher than those of similar risk, it is underpriced and should be bought If a security’s yield is lower than those of similar risk, it is overpriced and should be sold Arbitrage is trading to profit from temporary price discrepancies in otherwise identical assets Copyright © 2004 by Thomson Southwestern All rights reserved.