1 Tensor correlation for He and Li isotopes

軽い核におけるテンソル相関と 短距離相関の役割 明 孝之 大阪大学 ＲＣＮＰ 1. Tensor correlation for He and Li isotopes in Tensor-Optimized Shell Model (TOSM) 2. Short-range correlation by Unitary Correlation Operator Method (UCOM) 3. TOSM + UCOM with bare interaction 核子と中間子の多体問題の統一的描像に向けて＠RCNP 2007. 12. 14 -15 1

Motivation (tensor force) • Tensor force (Vtensor) plays a significant role in the nuclear structure. – In 4 He, – ~ 80% (GFMC) R. B. Wiringa, S. C. Pieper, J. Carlson, V. R. Pandharipande, PRC 62(2001) • We would like to understand the role of Vtensor in the nuclear structure by describing tensor correlation explicitly. • model wave function (shell model and cluster model). • spatial properties, p-h correlation, … • Spectroscopy of neutron-rich nuclei : He and Li isotopes 2

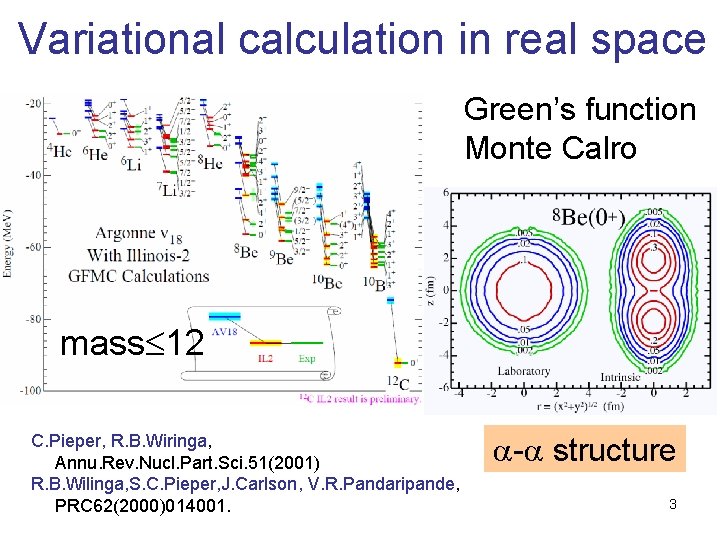
Variational calculation in real space Green’s function Monte Calro mass 12 C. Pieper, R. B. Wiringa, Annu. Rev. Nucl. Part. Sci. 51(2001) R. B. Wilinga, S. C. Pieper, J. Carlson, V. R. Pandaripande, PRC 62(2000)014001. a-a structure 3

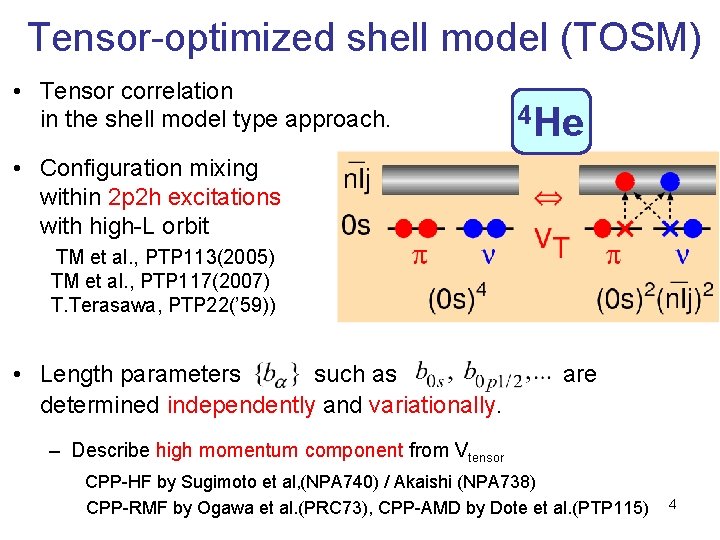
Tensor-optimized shell model (TOSM) • Tensor correlation in the shell model type approach. 4 He • Configuration mixing within 2 p 2 h excitations with high-L orbit TM et al. , PTP 113(2005) TM et al. , PTP 117(2007) T. Terasawa, PTP 22(’ 59)) • Length parameters such as determined independently and variationally. are – Describe high momentum component from Vtensor CPP-HF by Sugimoto et al, (NPA 740) / Akaishi (NPA 738) CPP-RMF by Ogawa et al. (PRC 73), CPP-AMD by Dote et al. (PTP 115) 4

Hamiltonian and variational equations TM, Sugimoto, Kato, Toki, Ikeda PTP 117(’ 07)257 • Effective interaction : Akaishi force (NPA 738) – G-matrix from AV 8’ with k. Q=2. 8 fm-1 – Long and intermediate ranges of Vtensor survive. – Adjust Vcentral to reproduce B. E. and radius of 4 He 5

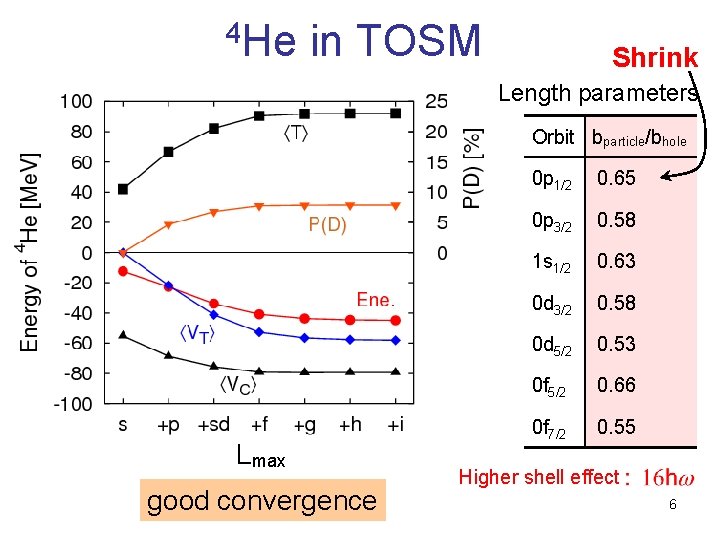
4 He in TOSM Shrink Length parameters Orbit bparticle/bhole Lmax good convergence 0 p 1/2 0. 65 0 p 3/2 0. 58 1 s 1/2 0. 63 0 d 3/2 0. 58 0 d 5/2 0. 53 0 f 5/2 0. 66 0 f 7/2 0. 55 Higher shell effect 6

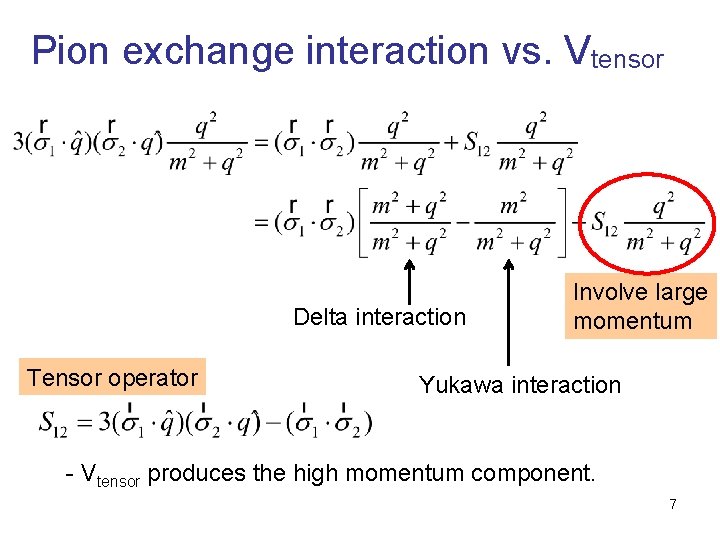
Pion exchange interaction vs. Vtensor Delta interaction Tensor operator Involve large momentum Yukawa interaction - Vtensor produces the high momentum component. 7

4 He in TOSM 28. 0 Energy (Me. V) 4 Gaussians instead of HO 51. 0 (0 s 1/2)4 85. 0 % (0 s 1/2)2 JT(0 p 1/2)2 JT JT=10 5. 0 JT=01 0. 3 (0 s 1/2)210(1 s 1/2)(0 d 3/2)10 2. 4 (0 s 1/2)210(0 p 3/2)(0 f 5/2)10 2. 0 P[D] 9. 6 c. m. excitation = 0. 6 Me. V • 0 of pion nature. • deuteron correlation with (J, T)=(1, 0) Cf. R. Schiavilla et al. (GFMC) PRL 98(’ 07)132501 8

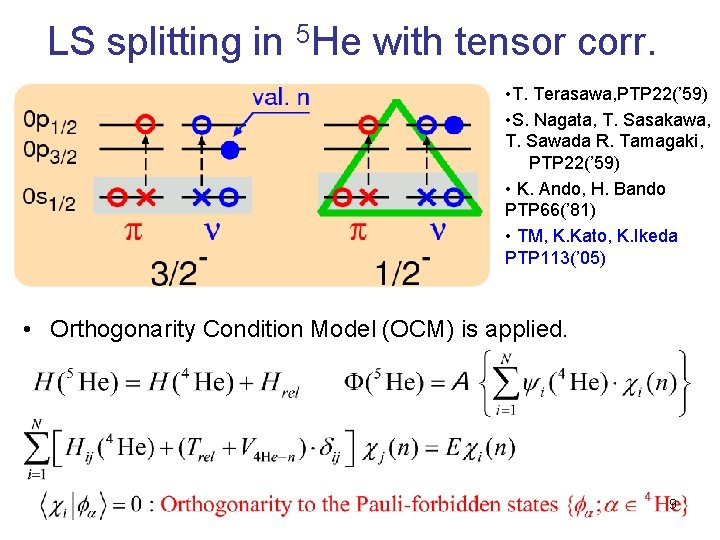
LS splitting in 5 He with tensor corr. • T. Terasawa, PTP 22(’ 59) • S. Nagata, T. Sasakawa, T. Sawada R. Tamagaki, PTP 22(’ 59) • K. Ando, H. Bando PTP 66(’ 81) • TM, K. Kato, K. Ikeda PTP 113(’ 05) • Orthogonarity Condition Model (OCM) is applied. 9

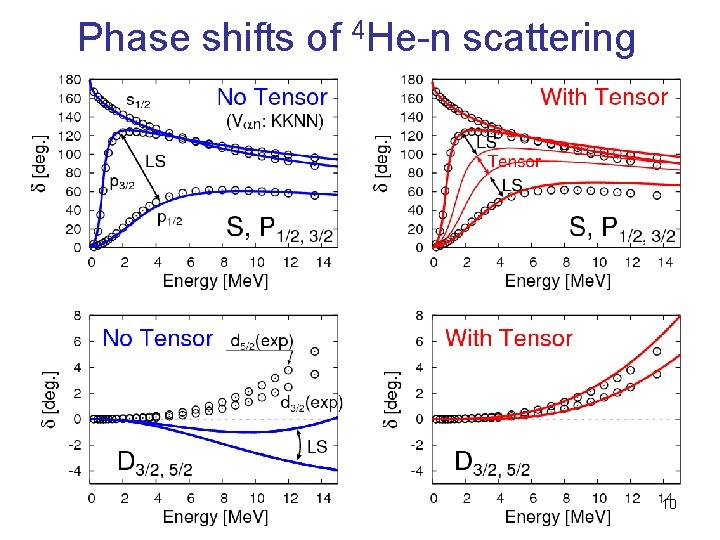
Phase shifts of 4 He-n scattering 10

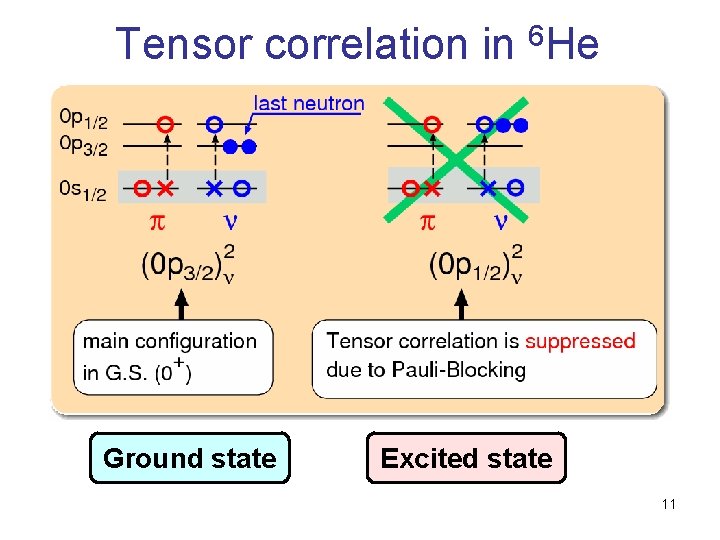
Tensor correlation in 6 He Ground state Excited state 11

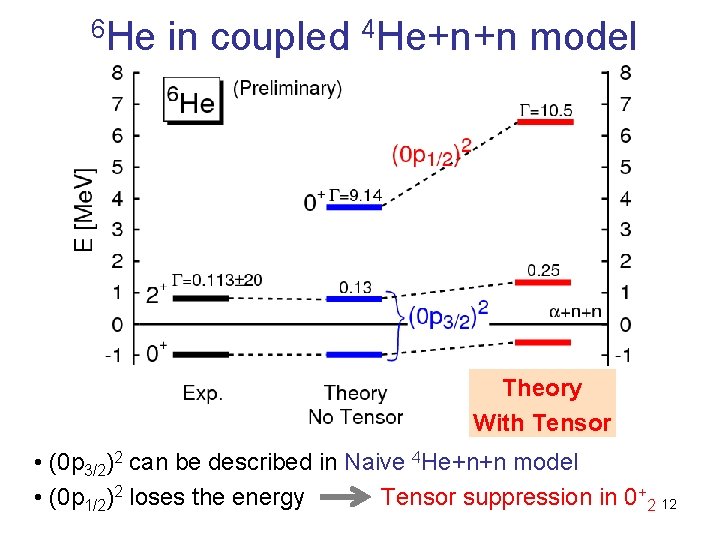
6 He in coupled 4 He+n+n model Theory With Tensor • (0 p 3/2)2 can be described in Naive 4 He+n+n model • (0 p 1/2)2 loses the energy Tensor suppression in 0+2 12

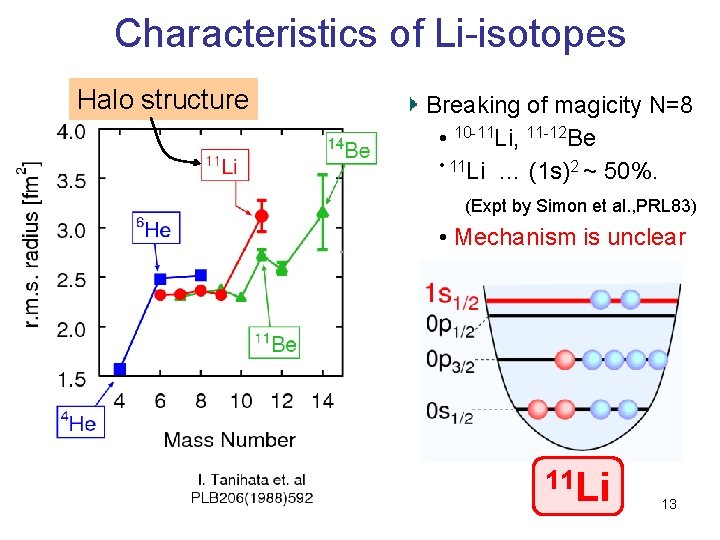
Characteristics of Li-isotopes Halo structure Breaking of magicity N=8 • 10 -11 Li, 11 -12 Be • 11 Li … (1 s)2 ~ 50%. (Expt by Simon et al. , PRL 83) • Mechanism is unclear 11 Li 13

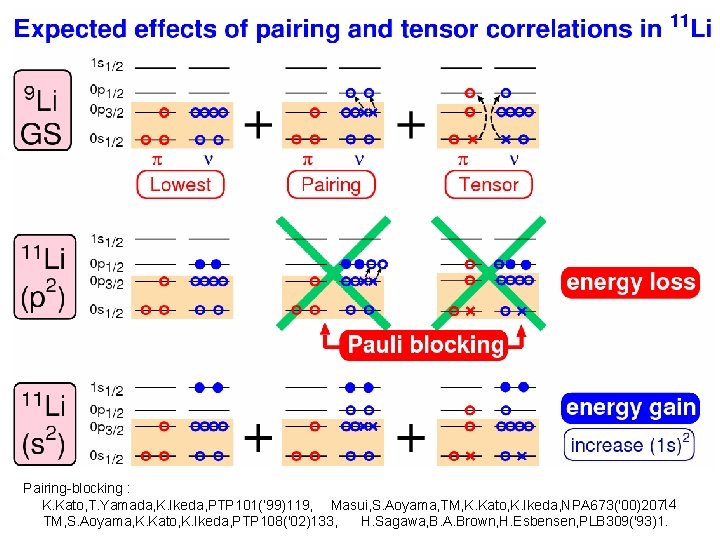
Pairing-blocking : 14 K. Kato, T. Yamada, K. Ikeda, PTP 101(‘ 99)119, Masui, S. Aoyama, TM, K. Kato, K. Ikeda, NPA 673('00)207. TM, S. Aoyama, K. Kato, K. Ikeda, PTP 108('02)133, H. Sagawa, B. A. Brown, H. Esbensen, PLB 309('93)1.

11 Li in coupled 9 Li+n+n model • System is solved based on RGM TOSM • Orthogonality Condition Model (OCM) is applied. 15

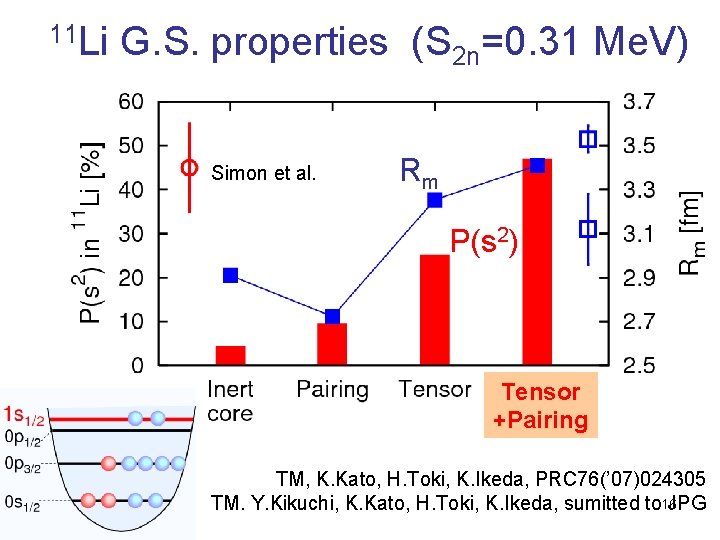
11 Li G. S. properties (S 2 n=0. 31 Me. V) Simon et al. Rm P(s 2) Tensor +Pairing TM, K. Kato, H. Toki, K. Ikeda, PRC 76(’ 07)024305 TM. Y. Kikuchi, K. Kato, H. Toki, K. Ikeda, sumitted to 16 JPG

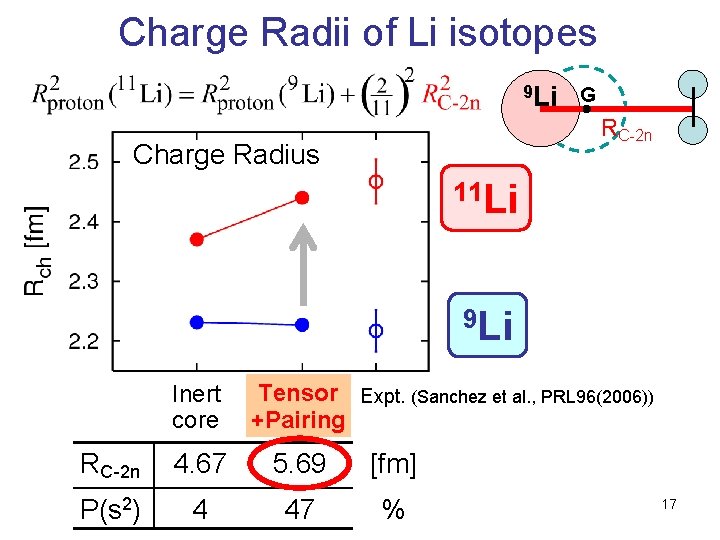
Charge Radii of Li isotopes 9 Li G RC-2 n Charge Radius 11 Li 9 Li Inert core Tensor Expt. (Sanchez et al. , PRL 96(2006)) +Pairing RC-2 n 4. 67 5. 69 [fm] P(s 2) 4 47 % 17

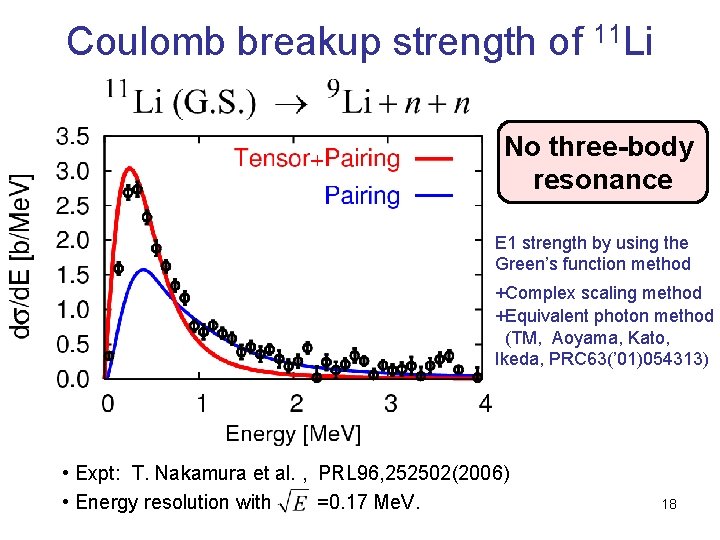
Coulomb breakup strength of 11 Li No three-body resonance E 1 strength by using the Green’s function method +Complex scaling method +Equivalent photon method (TM, Aoyama, Kato, Ikeda, PRC 63(’ 01)054313) • Expt: T. Nakamura et al. , PRL 96, 252502(2006) • Energy resolution with =0. 17 Me. V. 18

Tensor & Short-range correlations • Tensor correlation in TOSM – – 2 p 2 h mixing optimizing the particle states (radial & high-L) • Short-range correlation – Short-range repulsion of the bare NN force in the relative wave function of nuclei – Unitary Correlation Operator Method (UCOM) H. Feldmeier, T. Neff, R. Roth, J. Schnack, NPA 632(1998)61 T. Neff, H. Feldmeier NPA 713(2003)311 19

Unitary Correlation Operator Method short-range correlator Bare Hamiltonian Shift operator depending on the relative distance r H. Feldmeier, T. Neff, R. Roth, J. Schnack, NPA 632(1998)61 20

Short-range correlator : C Original r 2 1 Ge. V repulsion C 21

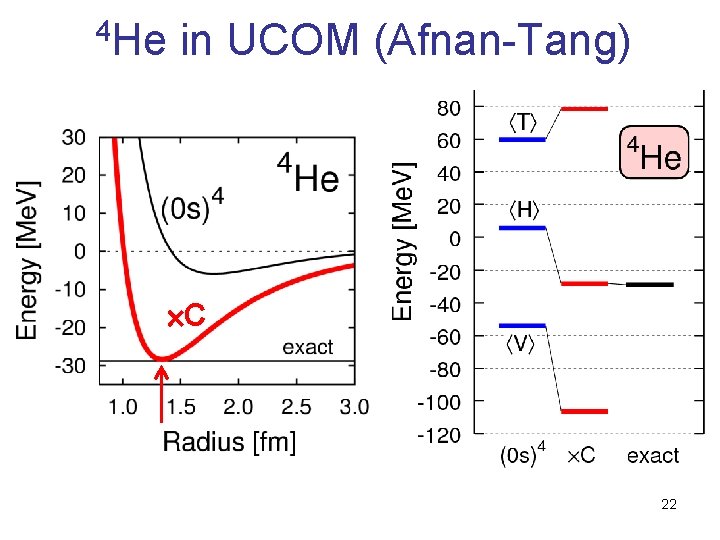
4 He in UCOM (Afnan-Tang) C 22

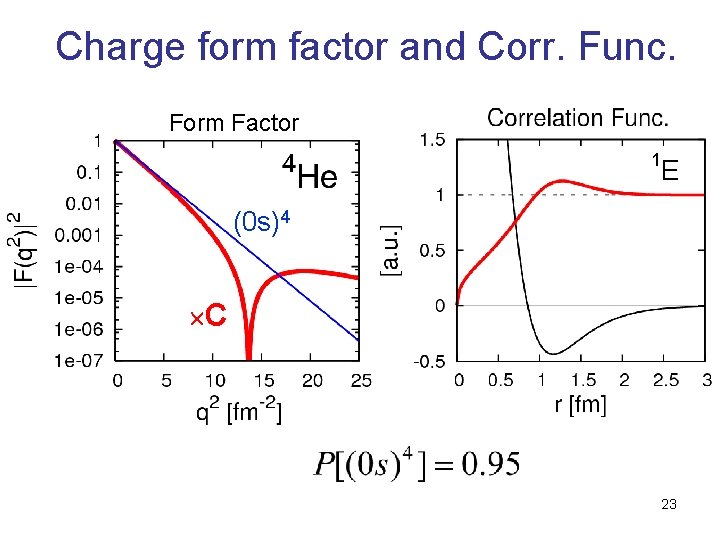
Charge form factor and Corr. Func. Form Factor 1 E (0 s)4 C 23

4 He in TOSM+UCOM Central+ LS+Tensor (Kamada et al. PRC 64) R. Roth et. al , PRC 72(2005)034002 24

Summary • Tensor correlation in nuclei – Tensor-optimized shell model (TOSM) – He isotopes, Li isotopes • Short-range correlation – Unitary Correlation Operator Method (UCOM) • In TOSM+UCOM, we can study the nuclear structure starting from the bare interaction – Spectroscopy of light nuclei (p-shell region) 25

4 He in TOSM+UCOM (0 s 1/2)4 88. 1 % (0 s 1/2)2 JT(0 p 1/2)2 JT JT=10 JT=01 Vnn : AV 8’ 3. 6 % 0. 1 (0 s 1/2)210(1 s 1/2)(0 d 3/2)10 1. 9 (0 s 1/2)210(0 p 3/2)(0 f 5/2)10 1. 6 P[D] 7. 6 c. m. excitation = 0. 4 Me. V • 0 - of pion nature • deuteron corr. with (J, T)=(1, 0) 26

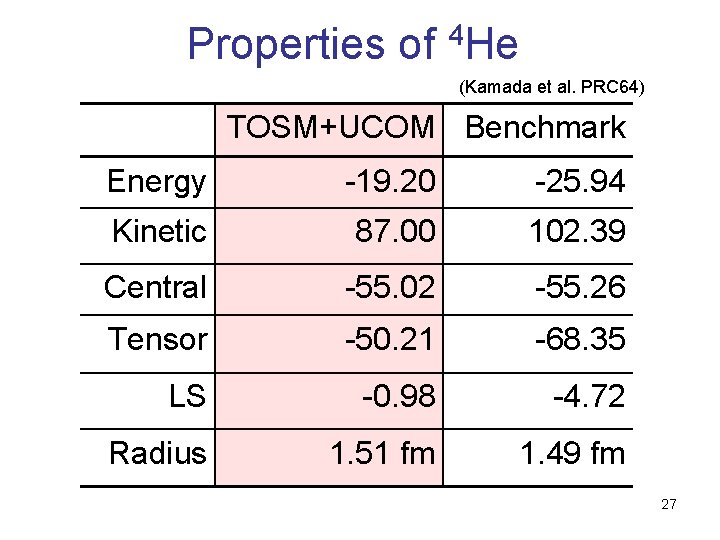
Properties of 4 He (Kamada et al. PRC 64) TOSM+UCOM Benchmark Energy -19. 20 -25. 94 Kinetic 87. 00 102. 39 Central -55. 02 -55. 26 Tensor -50. 21 -68. 35 LS -0. 98 -4. 72 Radius 1. 51 fm 1. 49 fm 27

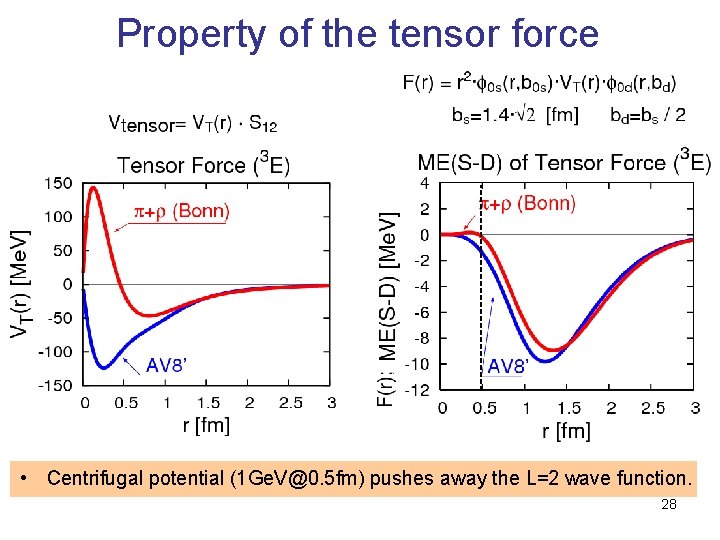
Property of the tensor force • Centrifugal potential (1 Ge. V@0. 5 fm) pushes away the L=2 wave function. 28

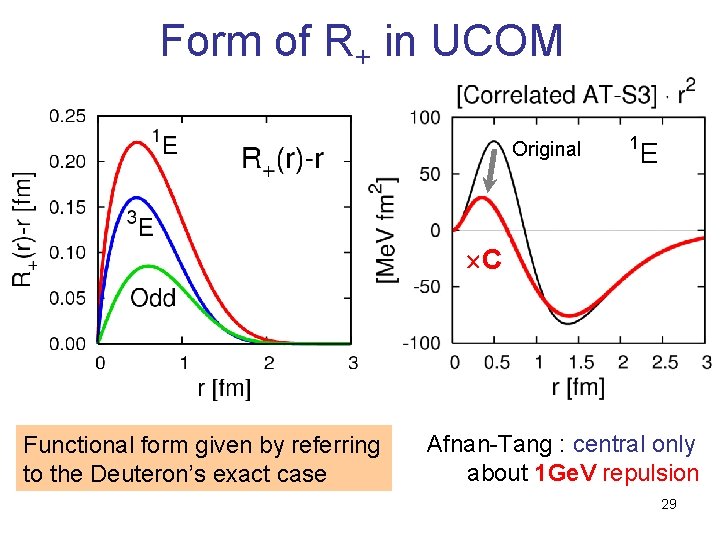
Form of R+ in UCOM Original 1 E C Functional form given by referring to the Deuteron’s exact case Afnan-Tang : central only about 1 Ge. V repulsion 29

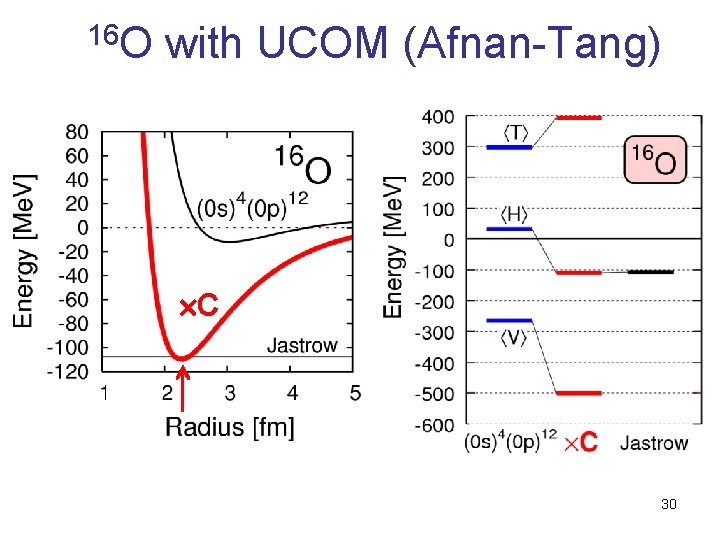
16 O with UCOM (Afnan-Tang) C 30

6 He with 4 He+n+n model V Pairing correlation is important V+T S. Aoyama, S. Mukai, K. Kato, K. Ikeda, PTP 93(1995)99. 31 K. Ikeda, NPA 538(1992)355

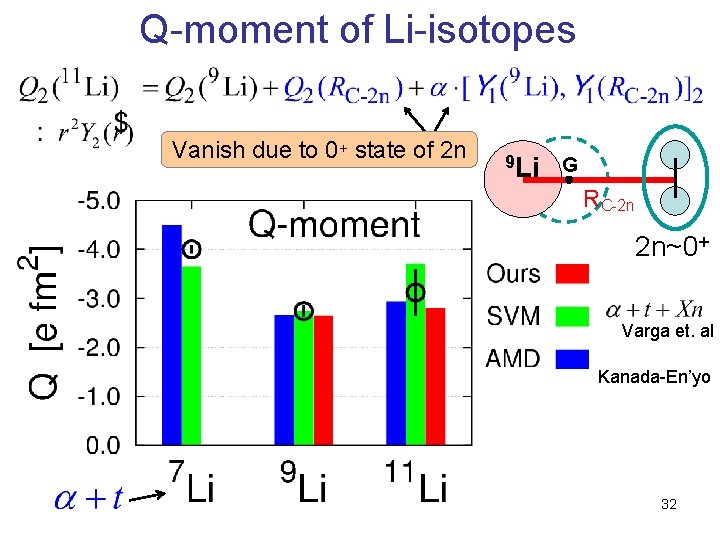
Q-moment of Li-isotopes Vanish due to 0+ state of 2 n 9 Li G RC-2 n 2 n~0+ Varga et. al Kanada-En’yo 32