1 st proof parallel postulate perpendicular postulate alternate

  • Slides: 14
Download presentation
1 st proof parallel postulate perpendicular postulate alternate interior angles theorem 2 nd proof

1 st proof parallel postulate perpendicular postulate alternate interior angles theorem 2 nd proof triangle sum theorem

B Given: ∆ABC <1 <2 Prove: <3 A C Statement Reason ∆ABC given <1

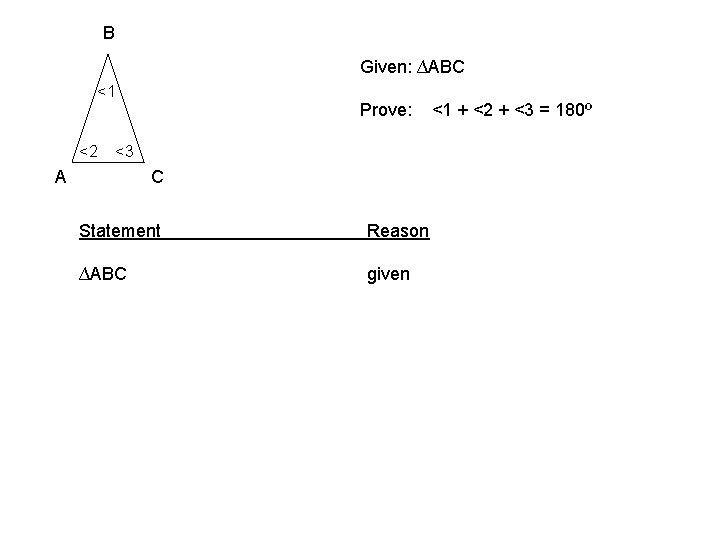
B Given: ∆ABC <1 <2 Prove: <3 A C Statement Reason ∆ABC given <1 + <2 + <3 = 180º

B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2

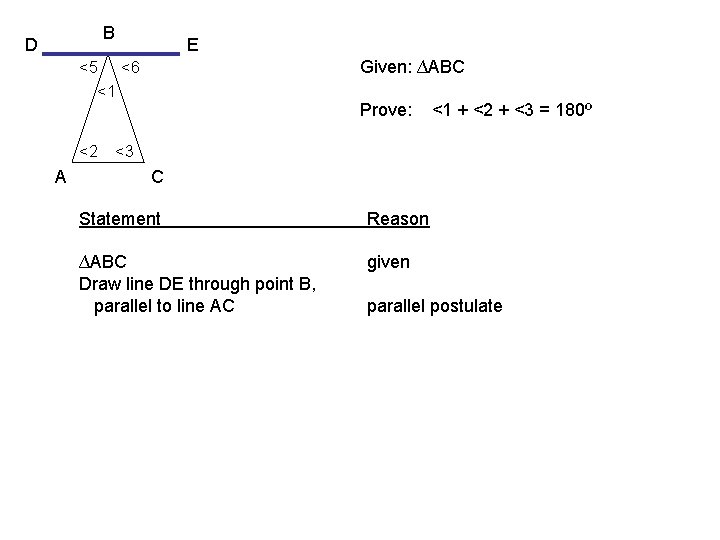
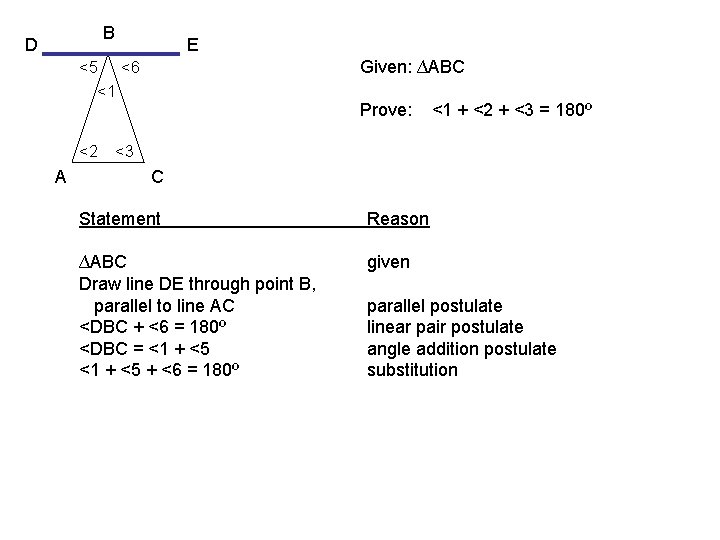
B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2 + <3 = 180º <3 C Statement Reason ∆ABC Draw line DE through point B, parallel to line AC given parallel postulate

B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2

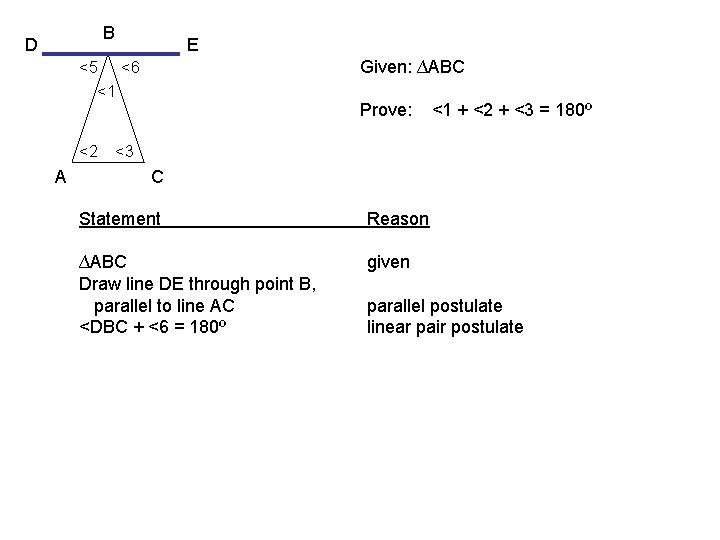
B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2 + <3 = 180º <3 C Statement Reason ∆ABC Draw line DE through point B, parallel to line AC <DBC + <6 = 180º given parallel postulate linear pair postulate

B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2

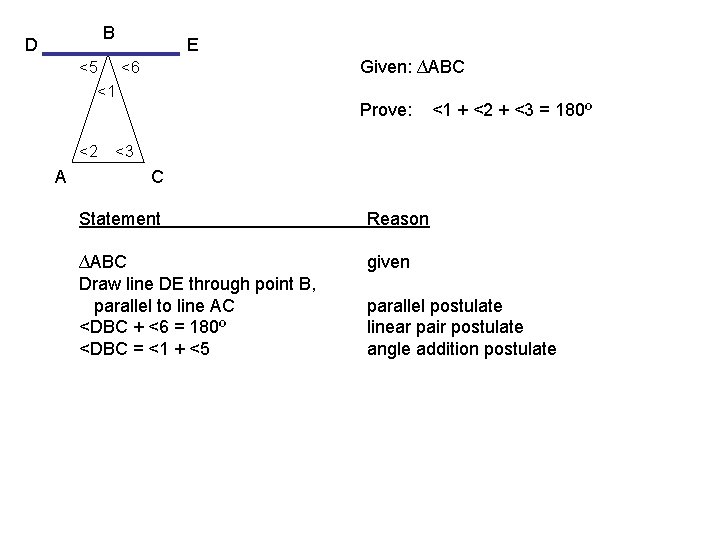
B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2 + <3 = 180º <3 C Statement Reason ∆ABC Draw line DE through point B, parallel to line AC <DBC + <6 = 180º <DBC = <1 + <5 given parallel postulate linear pair postulate angle addition postulate

B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2

B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2 + <3 = 180º <3 C Statement Reason ∆ABC Draw line DE through point B, parallel to line AC <DBC + <6 = 180º <DBC = <1 + <5 + <6 = 180º given parallel postulate linear pair postulate angle addition postulate substitution

B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2

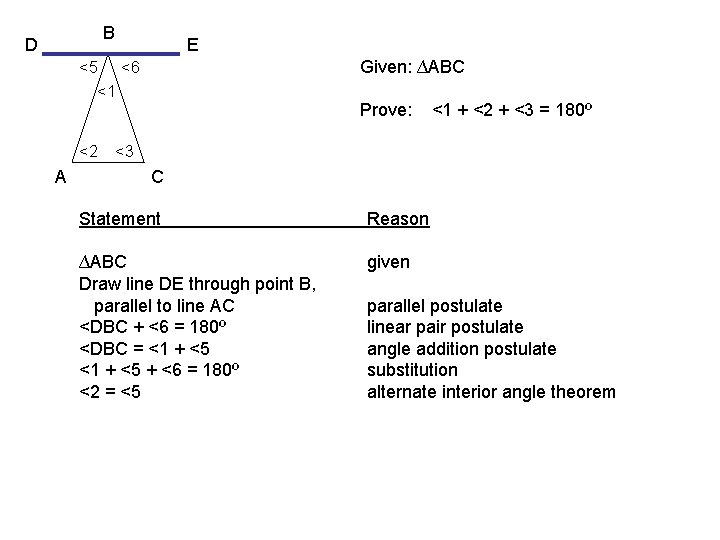
B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2 + <3 = 180º <3 C Statement Reason ∆ABC Draw line DE through point B, parallel to line AC <DBC + <6 = 180º <DBC = <1 + <5 + <6 = 180º <2 = <5 given parallel postulate linear pair postulate angle addition postulate substitution alternate interior angle theorem

B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2

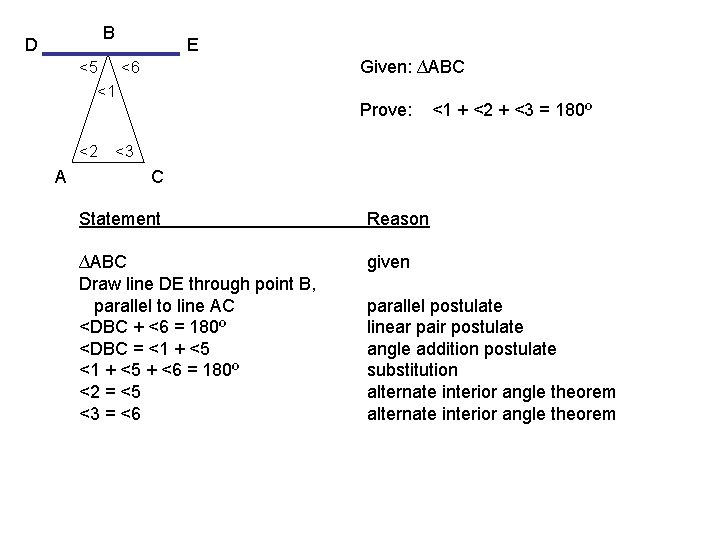
B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2 + <3 = 180º <3 C Statement Reason ∆ABC Draw line DE through point B, parallel to line AC <DBC + <6 = 180º <DBC = <1 + <5 + <6 = 180º <2 = <5 <3 = <6 given parallel postulate linear pair postulate angle addition postulate substitution alternate interior angle theorem

B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2

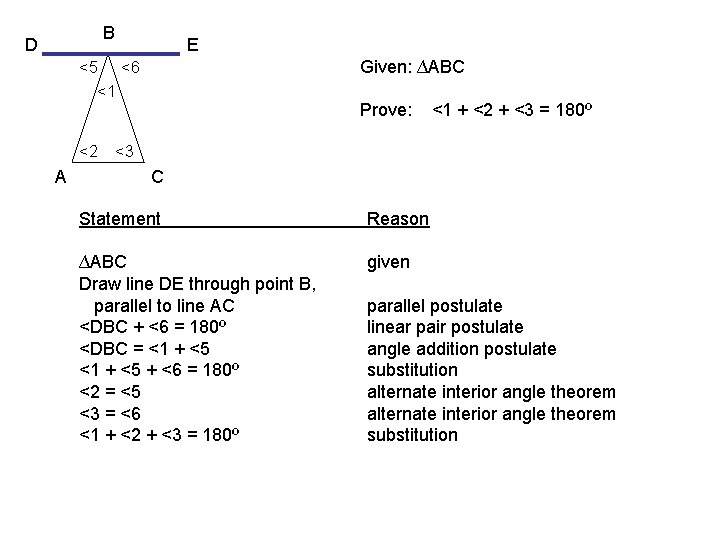
B D E Given: ∆ABC <5 <6 <1 <2 A Prove: <1 + <2 + <3 = 180º <3 C Statement Reason ∆ABC Draw line DE through point B, parallel to line AC <DBC + <6 = 180º <DBC = <1 + <5 + <6 = 180º <2 = <5 <3 = <6 <1 + <2 + <3 = 180º given parallel postulate linear pair postulate angle addition postulate substitution alternate interior angle theorem substitution

B Given: ∆ABC <1 <2 Prove: <3 <4 A C D Statement Reason ∆ABC

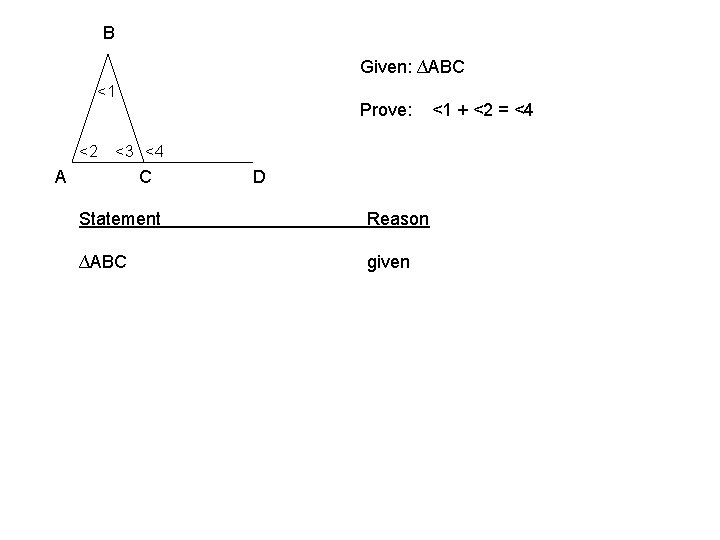
B Given: ∆ABC <1 <2 Prove: <3 <4 A C D Statement Reason ∆ABC given <1 + <2 = <4

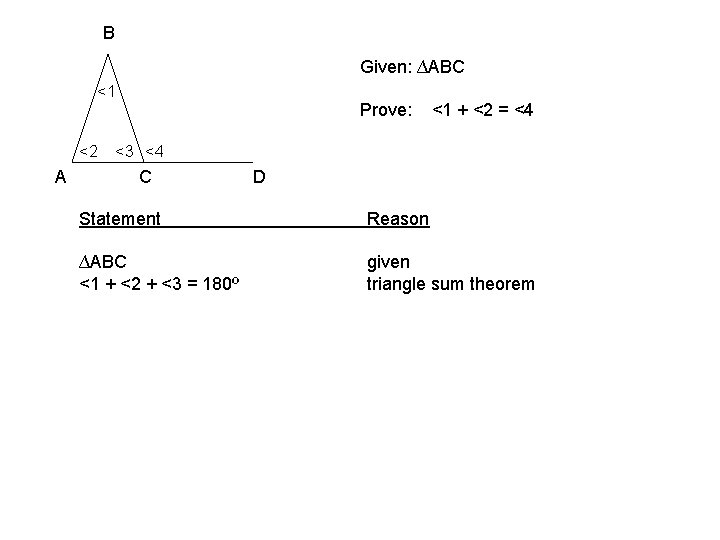
B Given: ∆ABC <1 <2 A Prove: <1 + <2 = <4 <3 <4

B Given: ∆ABC <1 <2 A Prove: <1 + <2 = <4 <3 <4 C D Statement Reason ∆ABC <1 + <2 + <3 = 180º given triangle sum theorem

B Given: ∆ABC <1 <2 A Prove: <1 + <2 = <4 <3 <4

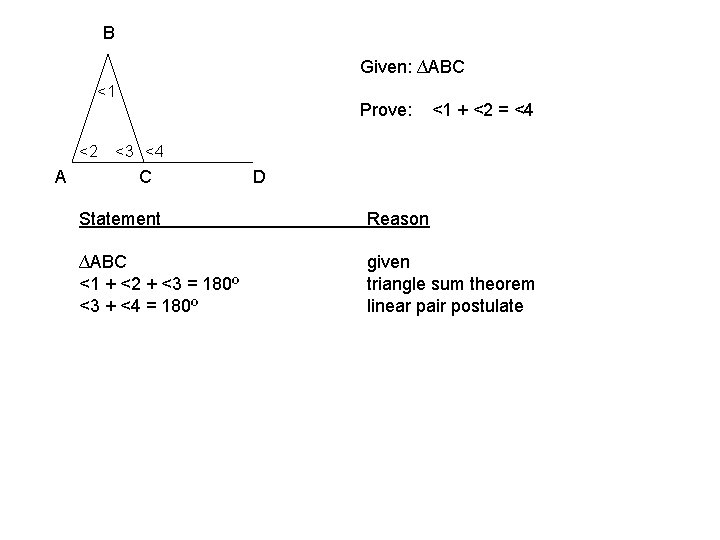
B Given: ∆ABC <1 <2 A Prove: <1 + <2 = <4 <3 <4 C D Statement Reason ∆ABC <1 + <2 + <3 = 180º <3 + <4 = 180º given triangle sum theorem linear pair postulate

B Given: ∆ABC <1 <2 A Prove: <1 + <2 = <4 <3 <4

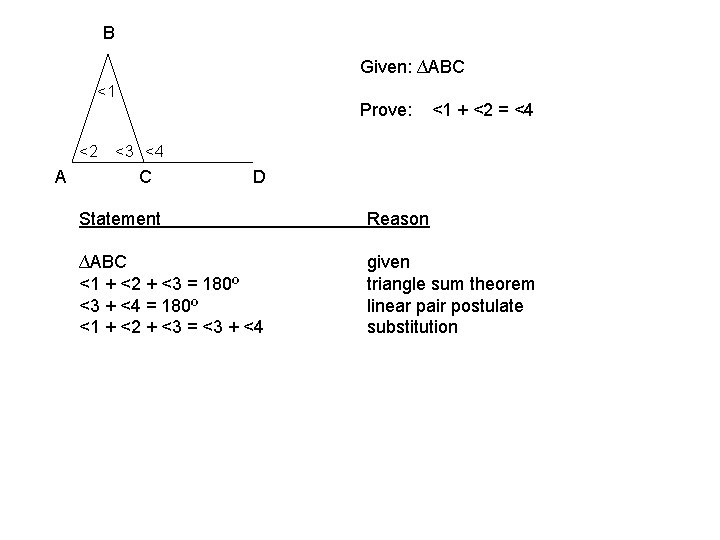
B Given: ∆ABC <1 <2 A Prove: <1 + <2 = <4 <3 <4 C D Statement Reason ∆ABC <1 + <2 + <3 = 180º <3 + <4 = 180º <1 + <2 + <3 = <3 + <4 given triangle sum theorem linear pair postulate substitution

B Given: ∆ABC <1 <2 A Prove: <1 + <2 = <4 <3 <4

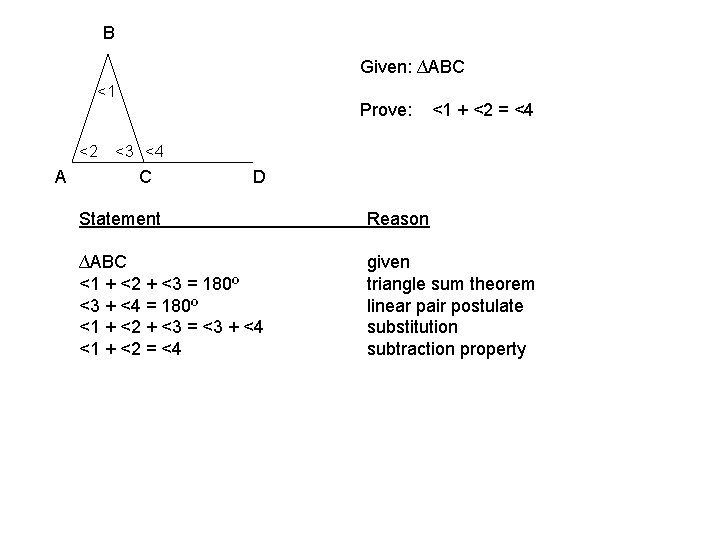
B Given: ∆ABC <1 <2 A Prove: <1 + <2 = <4 <3 <4 C D Statement Reason ∆ABC <1 + <2 + <3 = 180º <3 + <4 = 180º <1 + <2 + <3 = <3 + <4 <1 + <2 = <4 given triangle sum theorem linear pair postulate substitution subtraction property