1 st order linear differential equation P Q

2 nd order linear differential equation: P, Q, R, G – continuous. If G(x)

2 nd order linear homogeneous differential equation with constant coefficients: Find r, s. t.

Case II. One real root Two linearly independent solutions are General solution: Case III.

Problems 1. Area between curves: Set up the area between the following curves: a)

5. L’Hospital Rule (Sec. 4. 4): Find Justify every time you apply L’Hospital rule!

Product rule Calculus Chain rule Implicit f-n Differentiation Quotient rule Differential equations Elementary f-ns:

Slides: 8

Download presentation

1 st order linear differential equation: P, Q – continuous. Algorithm: Find I(x), s. t. by solving differential equation for I(x): then integrate both sides of the equation: Simplify the expression, if possible.

2 nd order linear differential equation: P, Q, R, G – continuous. If G(x) 0 equation is homogeneous, otherwise – nonhomogeneous. 2 nd order linear homogeneous differential equation – 1). If y 1 and y 2 are solutions, then y=c 1 y 1+c 2 y 2 (linear combination) is also a solution. 2). If y 1 and y 2 are linearly independent solutions and P 0, then the general solution is y=c 1 y 1+c 2 y 2.

2 nd order linear homogeneous differential equation with constant coefficients: Find r, s. t. y(x)=erx is a solution (substitute into the equation): characteristic equation Case I. Two unequal real roots Therefore, 2 linearly independent solutions General solution: and

Case II. One real root Two linearly independent solutions are General solution: Case III. Two complex roots Two linearly independent solutions General solution:

Problems 1. Area between curves: Set up the area between the following curves: a) b) Sec. 6. 1 5 -26 2. Volumes by washer method (Sec. 6. 2) and by cylindrical shells method (Sec 6. 3): Find the volume of the solid obtained by rotating the region bounded by about x=-1. 3. Arclength (Sec. 8. 1): Find the arclength of the curve 4. Approximate integration (Sec. 7. 7). Rn, Ln, Mn, Tn, Sn, formulae and error approximation: How large should we take n for Trapezoid / Midpoint / Simpson’s Rules in order to guarantee that the error of each method for Write down the expressions for R 5, L 5, M 5, T 5, S 5. would be within 0. 001?

5. L’Hospital Rule (Sec. 4. 4): Find Justify every time you apply L’Hospital rule! 6. Improper integral (Sec. 7. 8): type I, type II. 7. Differential equations: 1 st order separable equation (Sec. 9. 3): 1 st order linear equation (Sec. 9. 6): 2 nd order linear equation (Sec. 17. 1): Initial Value Problem and Boundary Value Problem. 8. Modeling: mixing problem, fish growth problem, population growth: The population of the world was 5. 28 billion in 1990 and 6. 07 billion in 2000. Assuming that the population growth rate is proportional to the size of population, formulate and solve the corresponding differential equation. Predict world population in 2020. When will the world population exceed 10 billion? 9. Recall: graphs and derivatives of elementary functions, integration techniques.

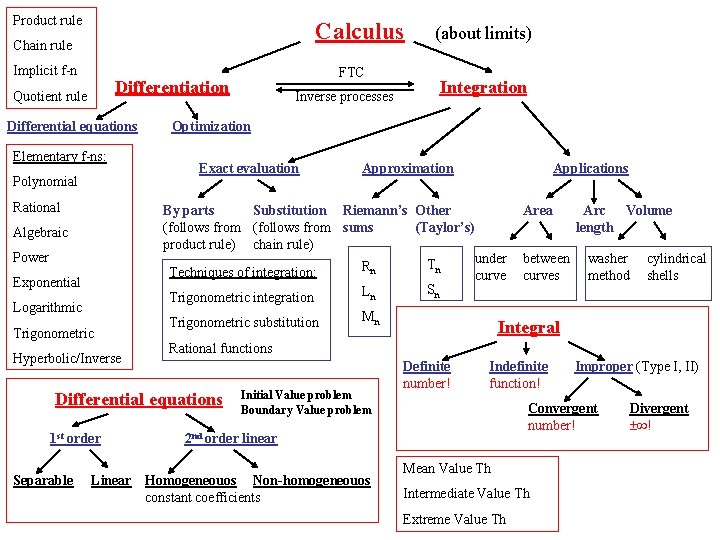
Product rule Calculus Chain rule Implicit f-n Differentiation Quotient rule Differential equations Elementary f-ns: Polynomial Rational Inverse processes Integration Optimization Exact evaluation Approximation Applications By parts Substitution Riemann’s Other (follows from sums (Taylor’s) product rule) chain rule) under Tn R n Techniques of integration: curve Sn Ln Trigonometric integration Algebraic Power Exponential Logarithmic Trigonometric Hyperbolic/Inverse Trigonometric substitution 1 st order Mn Area between curves Arc Volume length washer method cylindrical shells Integral Rational functions Differential equations Separable FTC (about limits) Initial Value problem Boundary Value problem Definite number! Indefinite function! Convergent number! 2 nd order linear Linear Homogeneouos Non-homogeneouos constant coefficients Improper (Type I, II) Mean Value Th Intermediate Value Th Extreme Value Th Divergent !