1 SPS 3 Students will distinguish the characteristics

1 SPS 3. Students will distinguish the characteristics and components of radioactivity. a. Differentiate among alpha and beta particles and gamma decay. b. Differentiate between fission and fusion. c. Explain the process half-life as related to radioactive decay. d. Describe nuclear energy, its practical application as an alternative energy source, and its potential problems Agenda -Nuclear Reactions: Decay (a, b, g) Fission Fusion -Decay Practice Problems (due tomorrow) -Chapter 10 Vocabulary (Due Tuesday) Name the 4 types of chemical reactions you have learned about: Synthesis, Decomposition, Single Replacement, Double Replacement • Name the 3 types of nuclear reactions:

2 Radioactivity

3 Nuclear Reactions • Large, unstable atoms undergo nuclear reactions to become more stable • There are 3 types of nuclear reactions: v. Fission v. Fusion v. Decay (alpha, beta, gamma)

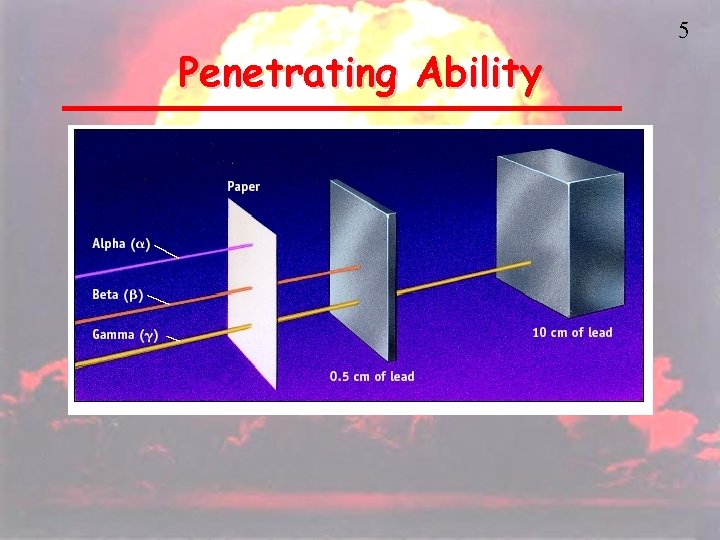
4 Types of Radiation • Alpha (a) – a positively charged helium isotope • Beta (β) – an electron • Gamma (γ) – pure energy; called a ray rather than a particle

Penetrating Ability 5

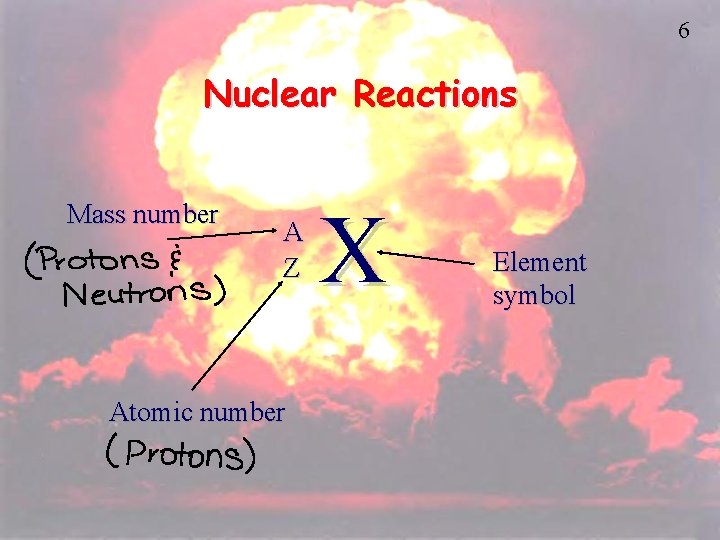
6 Nuclear Reactions Mass number A Z Atomic number X Element symbol

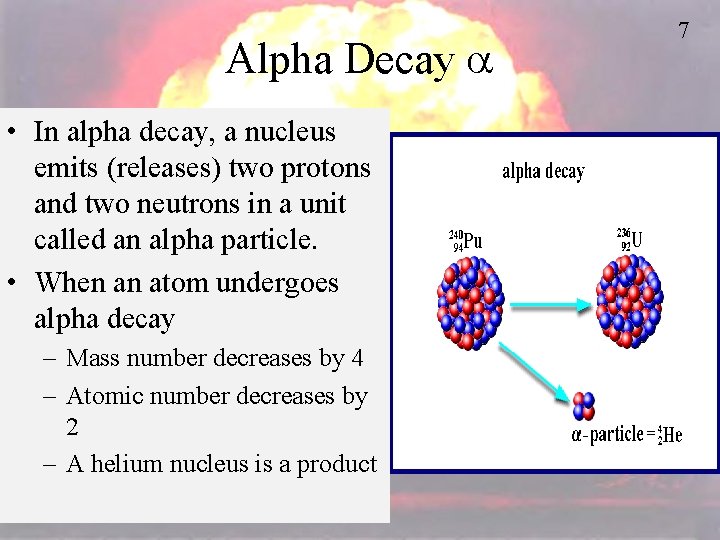
Alpha Decay a • In alpha decay, a nucleus emits (releases) two protons and two neutrons in a unit called an alpha particle. • When an atom undergoes alpha decay – Mass number decreases by 4 – Atomic number decreases by 2 – A helium nucleus is a product 7

8 Alpha Decay • U-239

9 Alpha Decay • U-241

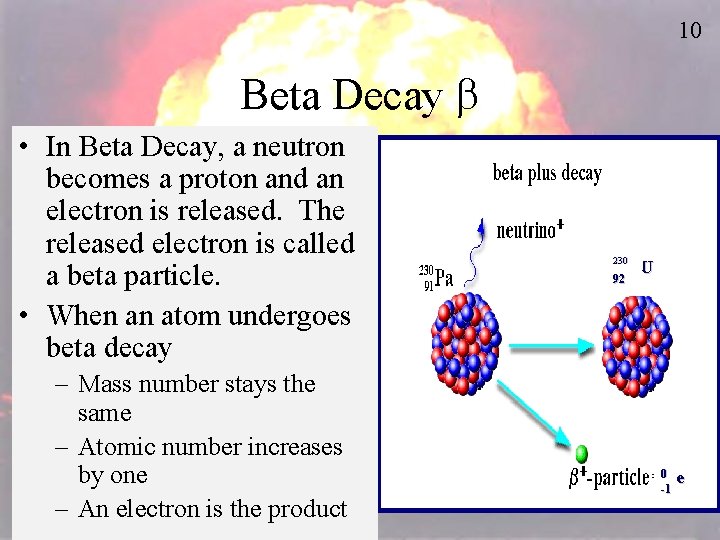
10 Beta Decay b • In Beta Decay, a neutron becomes a proton and an electron is released. The released electron is called a beta particle. • When an atom undergoes beta decay – Mass number stays the same – Atomic number increases by one – An electron is the product 230 236 92 U 0 e -1

11 Beta Decay • C-14

12 Beta Decay • C-16

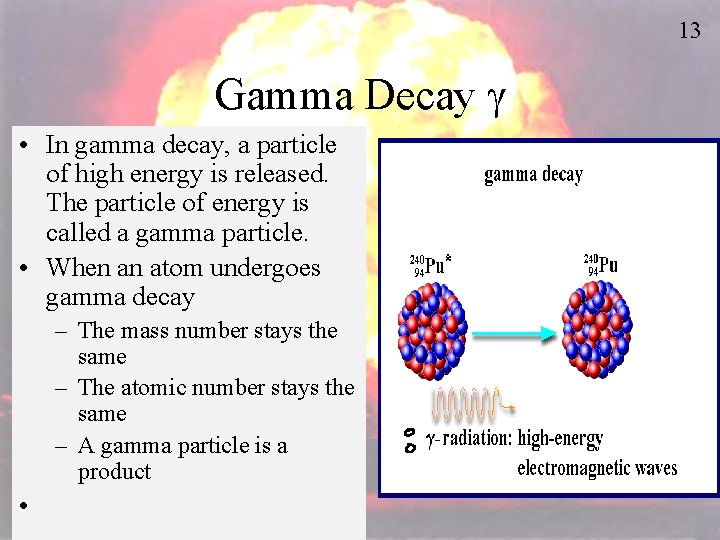
13 Gamma Decay g • In gamma decay, a particle of high energy is released. The particle of energy is called a gamma particle. • When an atom undergoes gamma decay – The mass number stays the same – The atomic number stays the same – A gamma particle is a product •

14 Gamma Decay • Ba-140

15 Gamma Decay • Ba-137

16 Nuclear Reactions • Gamma emission 14 N 7 + 0 g 0

Nuclear Reactions • Alpha emission 17

Nuclear Reactions • Beta emission 18

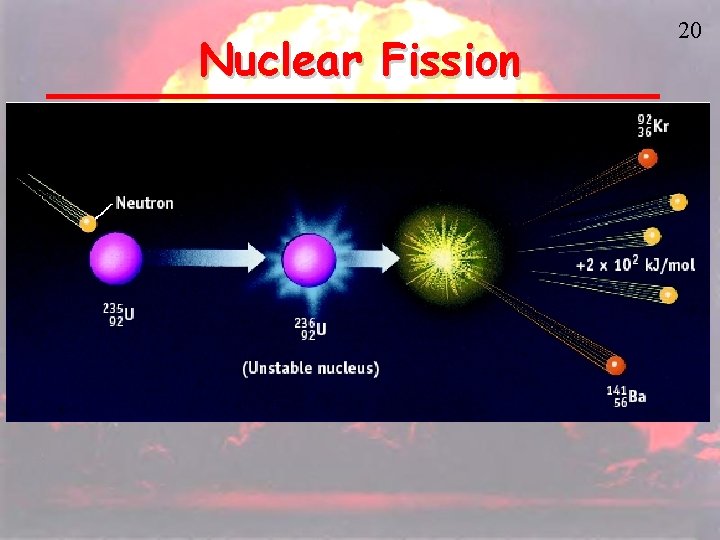
Nuclear Fission • Fission is the splitting of atoms • These are usually very large atoms, so that they are unstable 19

Nuclear Fission 20

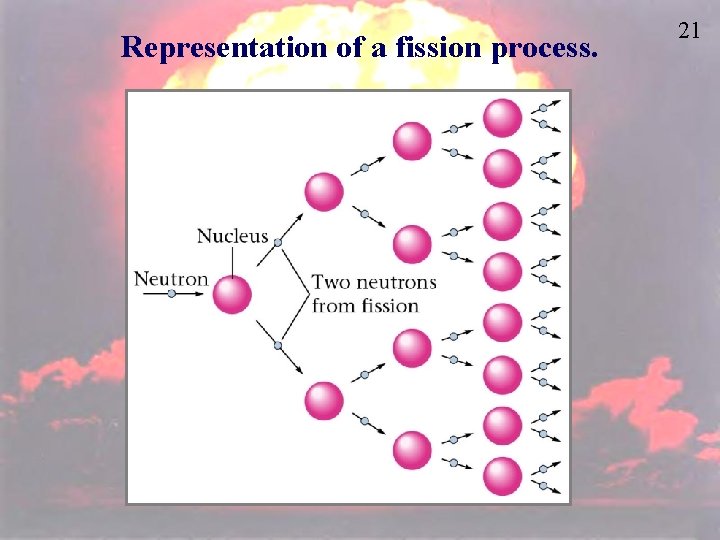
Representation of a fission process. 21

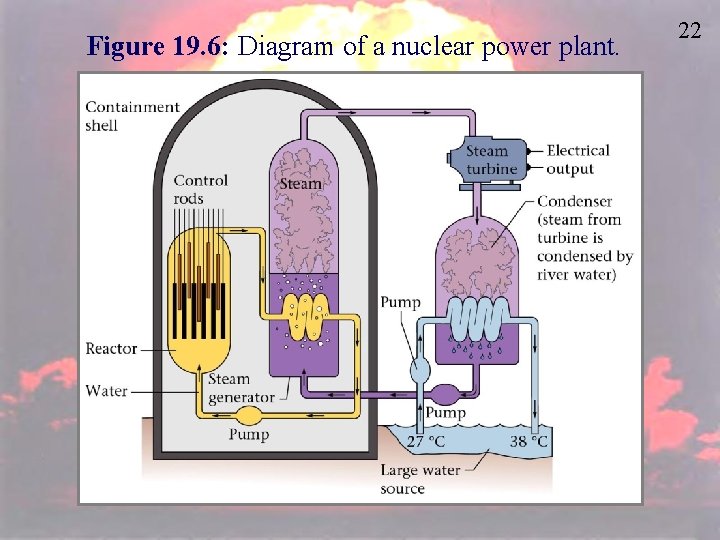
Figure 19. 6: Diagram of a nuclear power plant. 22

23 Nuclear Fusion small nuclei combine 2 H + 3 H 4 He + 1 n + 1 2 0 Occurs in the sun and other stars Energy

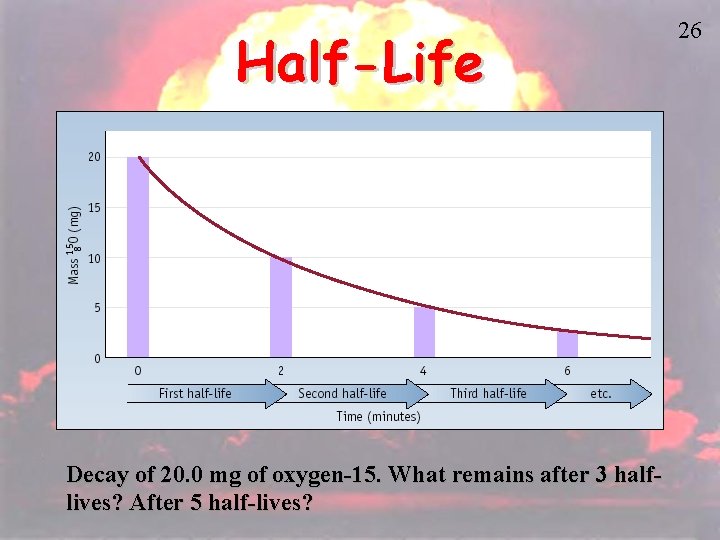
Half-Life The time that it takes for 1/2 a radioactive isotope to decay 24

Example of Radioactive Decay For example: Ra-234 has a half-life of 3. 6 days If you start with 50 grams of Ra-234 After 3. 6 days > 25 grams After 7. 2 days > 12. 5 grams After 10. 8 days > 6. 25 grams 25

Half-Life Decay of 20. 0 mg of oxygen-15. What remains after 3 halflives? After 5 half-lives? 26

27 Learning Check! The half life of I-123 is 13 hr. How much of a 64 mg sample of I-123 is left after 39 hours?

28 SPS 3. Students will distinguish the characteristics and components of radioactivity. a. Differentiate among alpha and beta particles and gamma radiation. b. Differentiate between fission and fusion. c. Explain the process half-life as related to radioactive decay. d. Describe nuclear energy, its practical application as an alternative energy source, and its potential problems • Name the 4 types of chemical reactions you have learned about: Synthesis, Decomposition, Single Replacement, Double Replacement • : Name the 3 types of nuclear reactions: • Fission, Fusion, Decay (alpha, beta, gamma)

Half-life Question & WORK The half-life of Iodine-131 is 8. 1 days. How long will it take for three-fourths of a sample of Iodine-131 to decay? Radon-222 is a radioactive gas with a half-life of 3. 82 days. How long will it take for fifteensixteenth of a sample of Radon-222 to decay? 29

Uranium-238 decays very slowly, with a half-life of 4. 47 billion years. What 30 percentage of a sample of Uranium -238 would remain after 13. 41 billion years? A sample of Strontium-90 is found to have decayed to one-eighth of its original amount after 87. 3 years. What is the half-life of strontium-90?

A sample of Francium-212 will decay to one-sixteenth its original amount after 80 minutes. What is the half-life of Francium-212? 31 The ratio of Carbon-14 to Carbon-12 in a prehistoric wooden artifact is measured to be one-eighth of the ratio measured in a fresh sample of wood from the same region. The half-life of carbon-14 is 5715 years. Determine its age.

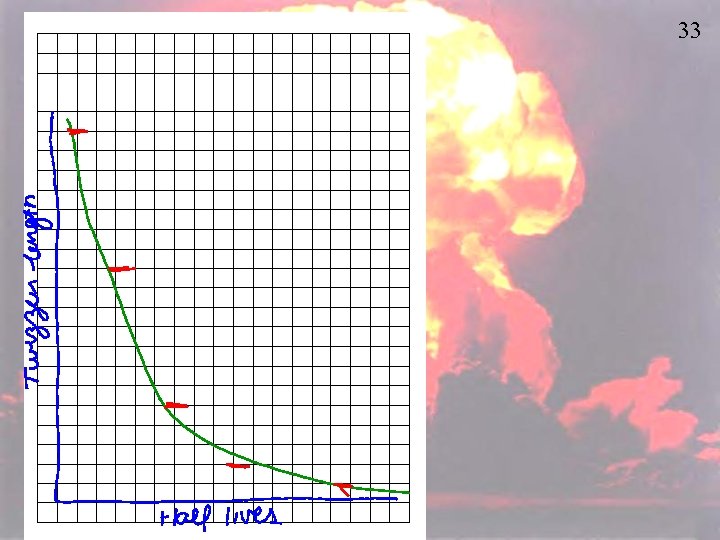
32 • Prepare axes on the graph paper for quadrant 1. The horizontal axis should be evenly marked in half-lives (0 -10) and the vertical axis labeled “Length of Twizzler. ” – (Note: the vertical axis should be long enough to accommodate the length of a single Twizzler. ) • Given 2 Twizzlers, place one of them along the vertical y-axis with one end touching the zero on the horizontal x-axis. • Cut the second Twizzler in half. Place one of the halves vertically on the graph over the 1 -half-life mark. • Cut the remaining piece in half. Put one of the halves vertically over the 2 -half-life mark. • Repeat until you reach the 10 half-life marker. • Place a mark the top of each Twizzler; connect the marks with a smooth curve of best fit. • Answer the questions.

33

1. How does the Twizzler length change 34 as time (in half-lives) increases? 2. What fraction of the Twizzler remains after 1, 2, 3, 4 half-lives? 3. The curve you drew is an exponential decay curve. List the important characteristics of such a curve. 4. If you had a 100 -gram sample of a material the mass of which decayed in the manner of your Twizzlers, how much of it would you have after 1 half-life? 2 half lives? 3 half lives? 5. Did the Twizzler ever completely disappear? Explain. 6. If you had started with a GIANT Twizzler (2 times the normal size), how would this have affected the shape of the graph? Explain.

35 • Distinguish the following types of nuclear decay: • Alpha • Beta • Gamma • What percent of a material remains after one half-life? 50%

36 • The amount of time it takes for 50% of a sample to undergo decay is called. . . Half-life • What fraction of a sample remains after 2 half-lives?

37 • The amount of time it take for 50% of a sample to undergo decay is called. . . Half-life • What fraction of a sample remains after 2 half-lives? 1/4

38 • How many half-lives does it take to reduce a sample to 1/8 its original mass? 3 • If it takes 30 seconds to reduce a sample from 16 g to 4 g what is the half-life of the material?

39

SPS 3. Students will distinguish the characteristics and components of radioactivity. d. Describe nuclear energy, its practical application as an alternative energy source, and its potential problems. 40

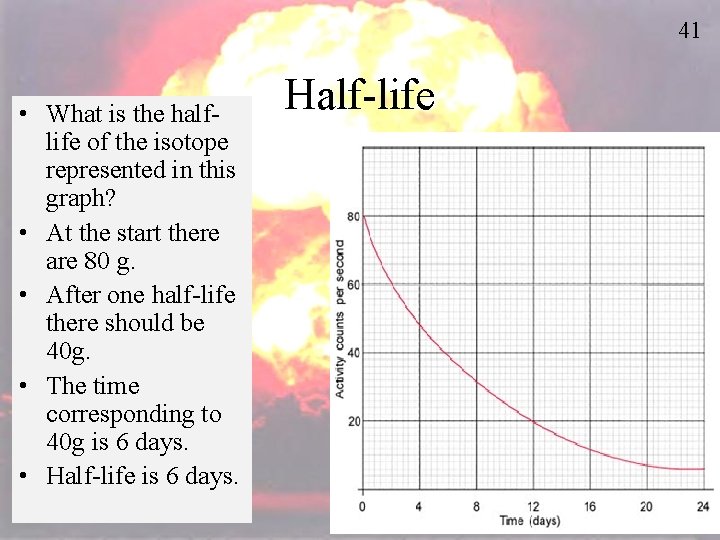
41 • What is the halflife of the isotope represented in this graph? • At the start there are 80 g. • After one half-life there should be 40 g. • The time corresponding to 40 g is 6 days. • Half-life is 6 days. Half-life

42 Half-life • S-24 t 1/2= 15 min How much remains from a 100 g sample after 1 hour? Mass Time 100 g 0 min

43 Half-life • I-131 t 1/2= 8 days How many days would it take to reduce a 300 g sample to 75 g? Mass Time

44 Half-life • C-14 t 1/2= 5, 730 years If you have 120 g remaining after 22920 years, what was the mass of your original sample? Mass (grams) Time (years) 120 22920

45 Pros and Cons of Nuclear Power • Most of our electricity is produced in coal fueled power plants. Nuclear fueled power plants can also be used to produce energy. • In a coal fueled power plant, coal is burned to produce heat. • In a nuclear fueled power plant, fission is used to produce heat.

46 Pros and Cons of Nuclear Power Advantages Disadvantages • Large amounts of energy are produced from very small amounts of nuclear material. • Nuclear material is not limited. • Very little pollution is released into the air. • Thermal pollution causes an increase in the temperature of water in rivers and streams. • Radioactive leaks can occur. • Nuclear waste must be stored in in special ways for very long periods of time.