1 Setelah menyaksikan tayangan ini anda dapat Menyelesaikan












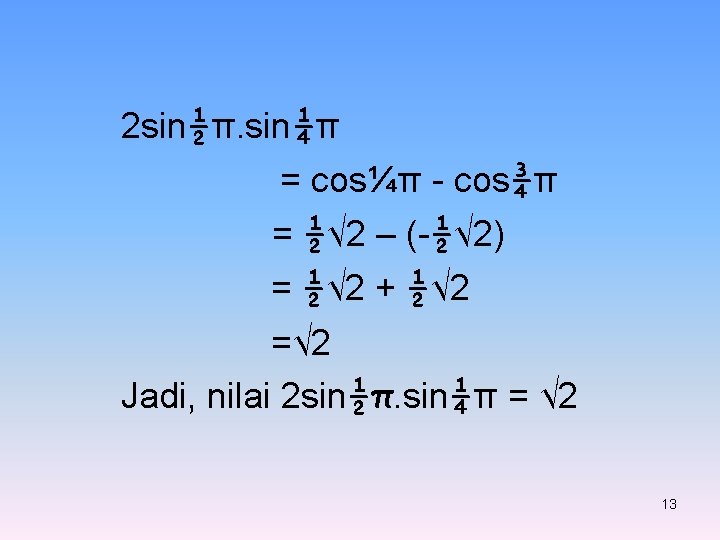



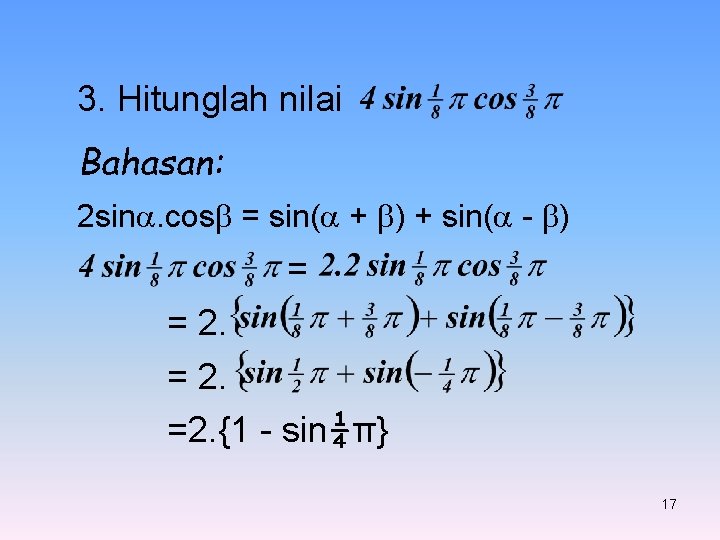
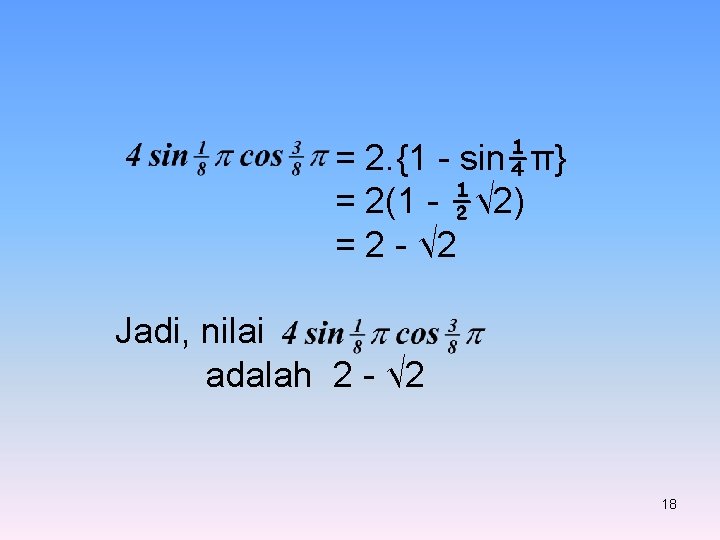

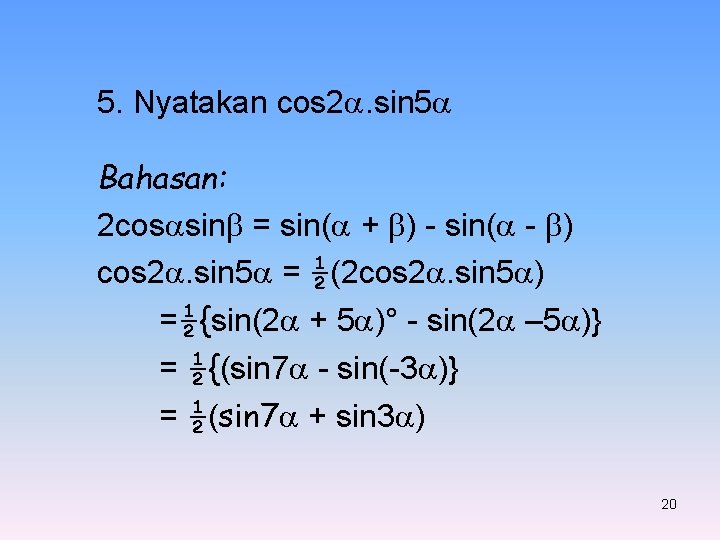

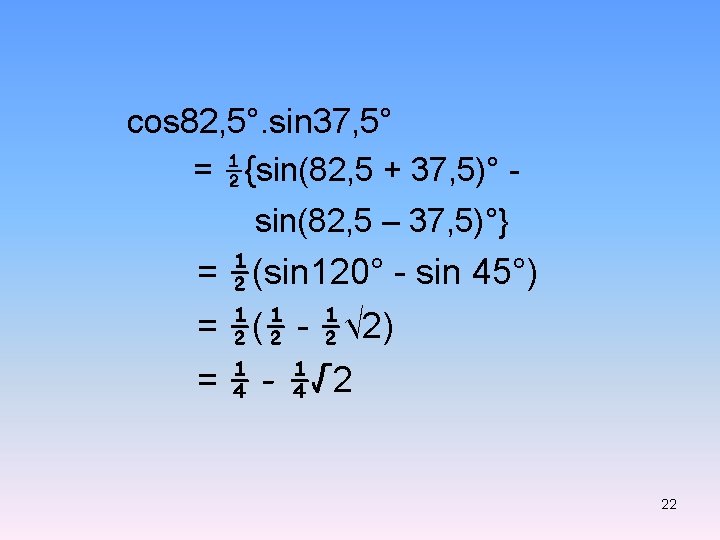




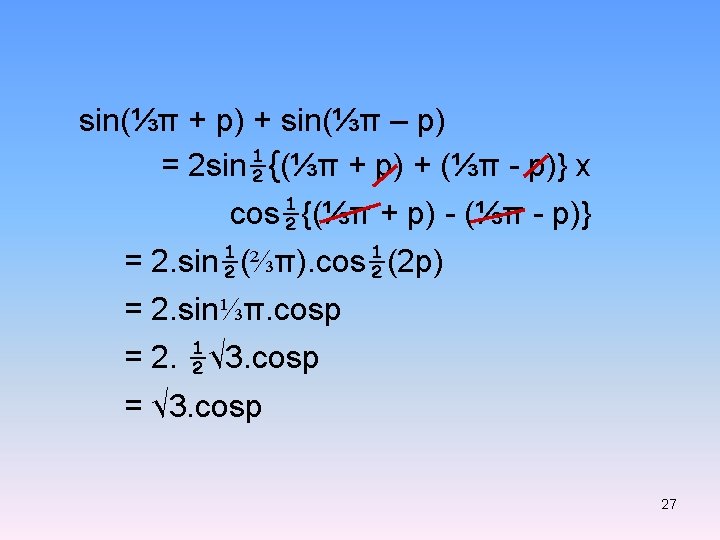


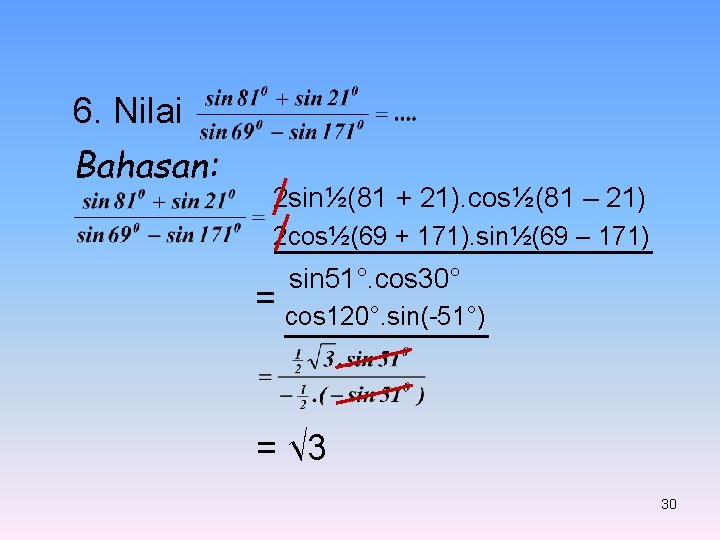




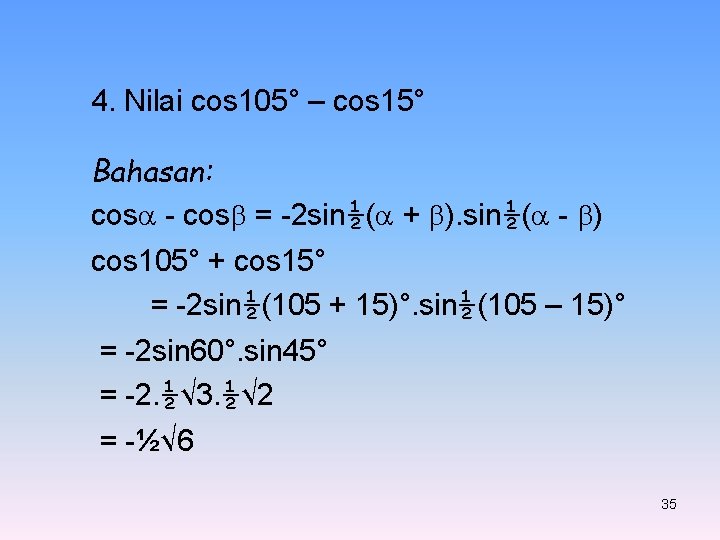



- Slides: 38

1

Setelah menyaksikan tayangan ini anda dapat Menyelesaikan soal yang berkaitan dengan rumus perkalian, jumlah dan selisih sinus dan cosinus 2

Rumus Perkalian kosinus 2 cos. cos = cos( + ) + cos( - ) 3

1. Nyatakan 2 cos 100°. cos 35° sebagai bentuk penjumlahan. Bahasan: 2 cos. cos = cos( + ) + cos( - ) 2 cos 100°. cos 35° = cos(100 + 35)° + cos(100 - 35)° = cos 135° + cos 65° 4

2. Nyatakan 2 cos 45°. cos 15° sebagai bentuk penjumlahan, kemudian tentukan nilainya. Bahasan: 2 cos. cos = cos( + ) + cos( - ) 2 cos 45°. cos 15° = cos(45 + 15)° + cos(45 - 15)° = cos 60° + cos 30° 5

2 cos 45°. cos 15° = cos 60° + cos 30° = ½ + ½√ 3 = ½(1 + √ 3) Jadi, nilai 2 cos 45°. cos 15° adalah ½(1 + √ 3) 6

3. Sederhanakan 2 cos(p + ¼π)cos(p - ¼π) Bahasan: 2 cos. cos = cos( + ) + cos( - ) 2 cos(p + ¼π). cos(p - ¼π) = cos{(p + ¼π) + (p - ¼π)} + cos{(p + ¼π) – (p - ¼π)} 7

2 cos(p + ¼π). cos(p - ¼π) = cos{(p + ¼π) + (p - ¼π)} + cos{(p + ¼π) – (p - ¼π)} = cos 2 p +cos½π = cos 2 p + 0 Jadi, bentuk sederhana dari 2 cos(p + ¼π). cos(p - ¼π) = cos 2 p 8

Rumus Perkalian Sinus 2 sin. sin = cos( - ) - cos( + ) 9

1. Nyatakan 2 sin 40°. sin 20° sebagai bentuk penjumlahan. Bahasan: 2 sin. sin = cos( - ) - cos( + ) 2 sin 40°. sin 20° = cos(40 - 20)° - cos(40 + 20)° = cos 20° - cos 60° = cos 20° - ½ 10

2. Hitunglah sin 75°. sin 15° Bahasan: 2 sin. sin = cos( - ) - cos( + ) sin 75°. sin 15° = ½(2 sin 75°. sin 15°) = ½{cos(75 - 15)° - cos(75 + 15)°} = ½(cos 60° - cos 90°) = ½( ½ - 0) = ¼ 11

3. Nyatakan bentuk 2 sin½π. sin¼π sebagai bentuk penjumlahan, kemudian tentukan nilainya. Bahasan: 2 sin. sin = cos( - ) - cos( + ) 2 sin½π. sin¼π = cos(½π - ¼π) - cos(½π + ¼π) = cos¼π - cos¾π 12
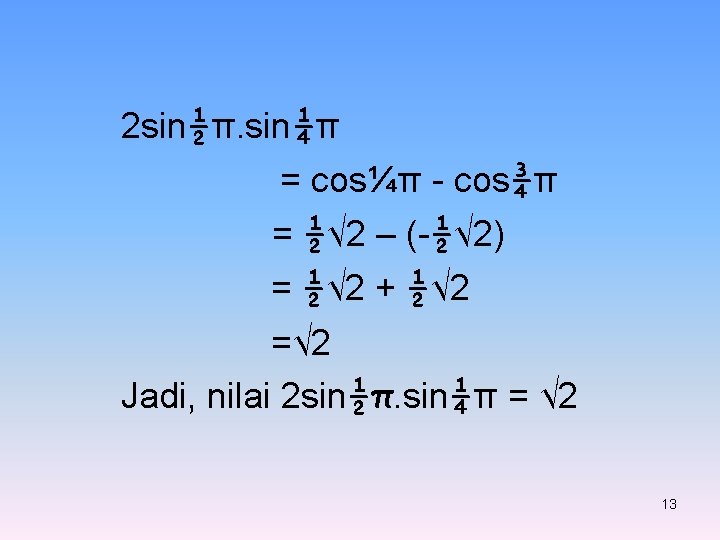

Rumus Perkalian sinus dan kosinus 2 sin. cos = sin( + ) + sin( - ) 2 cos. sin = sin( + ) – sin( - ) 14

1. Nyatakan 2 sin 80°. cos 50° sebagai bentuk penjumlahan. Bahasan: 2 sin cos = sin( + ) + sin( - ) 2 sin 80°cos 50° = sin(80 + 50)° + sin(80 - 50)° = sin 130° + sin 30° = sin 130 + ½ 15

2. Nyatakan 2 sin 3 A. cos. A sebagai bentuk penjumlahan. Bahasan: 2 sin cos = sin( + ) + sin( - ) 2 sin 3 Acos. A = sin(3 A + A)° + sin(3 A - A)° = sin 4 A + sin A 16
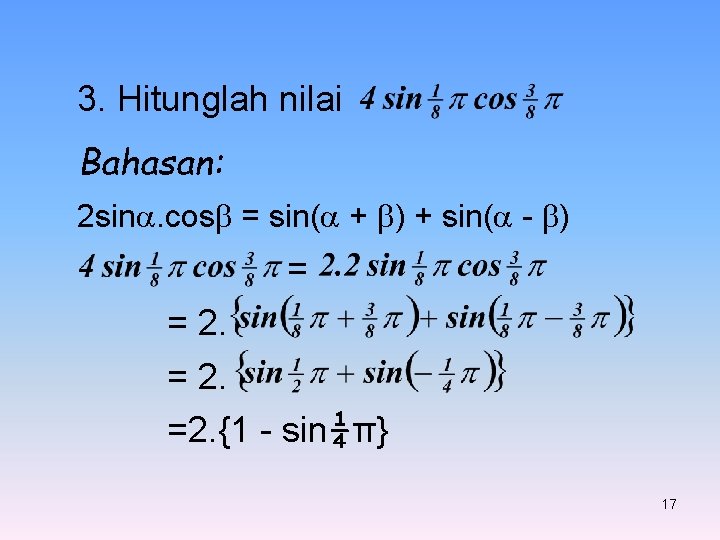
3. Hitunglah nilai Bahasan: 2 sin. cos = sin( + ) + sin( - ) = = 2. =2. {1 - sin¼π} 17
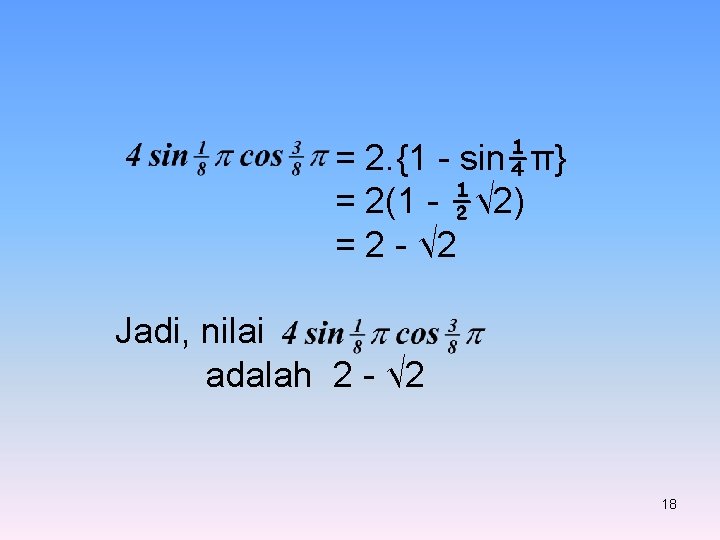
= 2. {1 - sin¼π} = 2(1 - ½√ 2) = 2 - √ 2 Jadi, nilai adalah 2 - √ 2 18

4. Sederhanakan bentuk 2 cos 75°. sin 15° Bahasan: 2 cos sin = sin( + ) - sin( - ) 2 cos 75°sin 15° = sin(75 + 15)° - sin(75 - 15)° = sin 90° - sin 60° = 1 - ½√ 3 19
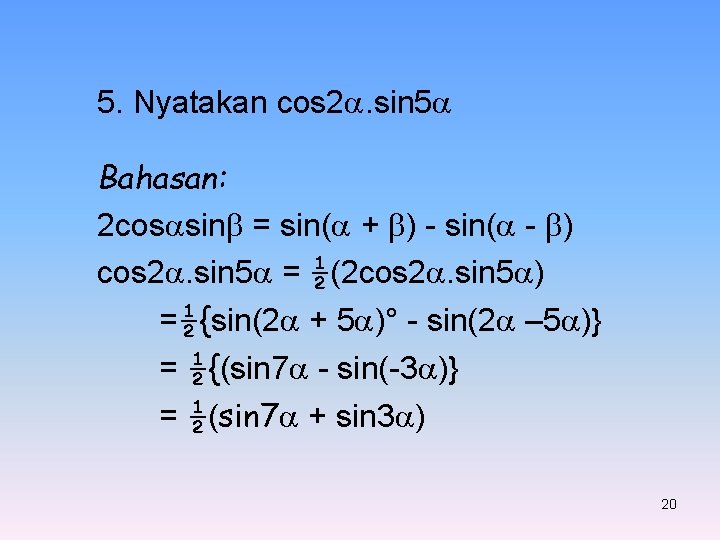
5. Nyatakan cos 2. sin 5 Bahasan: 2 cos sin = sin( + ) - sin( - ) cos 2. sin 5 = ½(2 cos 2. sin 5 ) =½{sin(2 + 5 )° - sin(2 – 5 )} = ½{(sin 7 - sin(-3 )} = ½(sin 7 + sin 3 ) 20

6. Hitunglah cos 82, 5°. sin 37, 5° Bahasan: 2 cos sin = sin( + ) - sin( - ) cos 82, 5°. sin 37, 5° = ½(2 cos 82, 5°. sin 37, 5°) = ½{sin(82, 5 + 37, 5)° sin(82, 5 – 37, 5)°} 21
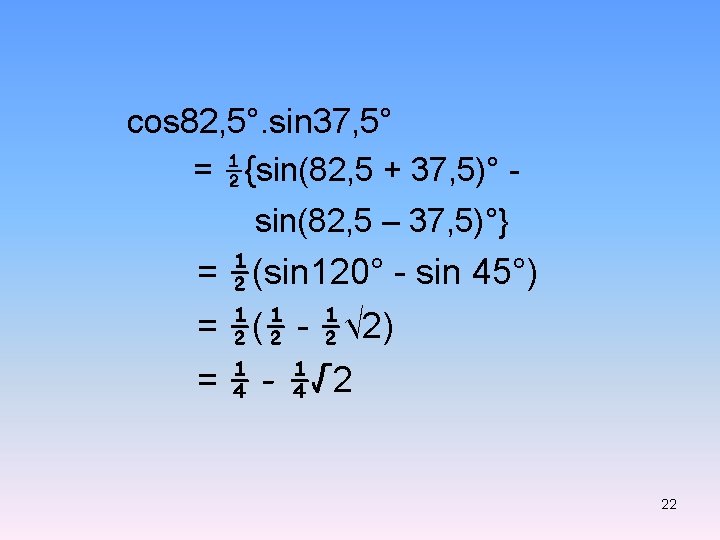
cos 82, 5°. sin 37, 5° = ½{sin(82, 5 + 37, 5)° sin(82, 5 – 37, 5)°} = ½(sin 120° - sin 45°) = ½(½ - ½√ 2) = ¼ - ¼√ 2 22

Rumus Jumlah dan selisih sinus sin + sin = 2 sin½( + ). cos½( - ) sin - sin = 2 cos½( + ). sin½( - ) 23

1. Nyatakan sin 6 A + sin 4 A sebagai bentuk perkalian. Bahasan: sin + sin = 2 sin½( + ). cos½( - ) sin 6 A + sin 4 A = 2 sin½(6 A + 4 A). cos½(6 A – 4 A) = 2 sin 5 A. cos. A 24

2. Sederhanakan sin 160° + sin 20° Bahasan: sin + sin = 2 sin½( + ). cos½( - ) sin 160° + sin 20° = 2 sin½(160 + 20)°. cos½(160 – 20)° = 2 sin 90°. cos 70° = 2. 1. cos 70° = cos 70° 25

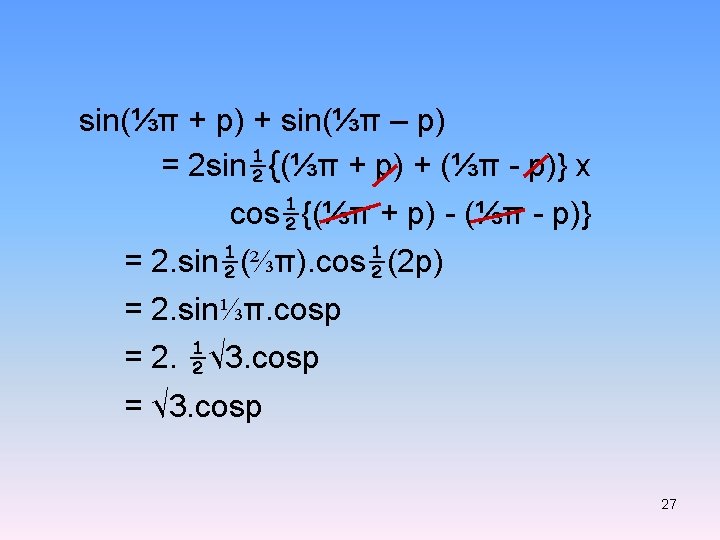

4. Nyatakan sin 4 x – sin 6 x sebagai bentuk perkalian. Bahasan: sin - sin = 2 cos½( + ). sin½( - ) sin 4 x – sin 6 x = 2 cos½(4 x + 6 x). sin½(4 x – 6 x) = 2 cos 5 x. sin(-x) = -2 cos 5 x. sinx 28

5. Sederhanakan sin 155° - sin 25° Bahasan: sin - sin = 2 cos½( + ). sin½( - ) sin 155° + sin 25° = 2 cos½(155 + 25)°. sin½(155 – 25)° = 2 cos 90°. sin 65° = 2. 0. sin 65° =0 29
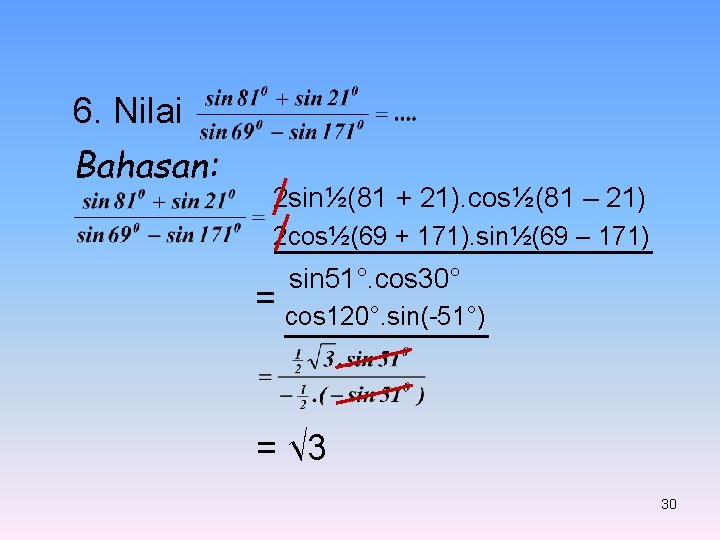
6. Nilai Bahasan: 2 sin½(81 + 21). cos½(81 – 21) 2 cos½(69 + 171). sin½(69 – 171) sin 51°. cos 30° = cos 120°. sin(-51°) = √ 3 30

Rumus Jumlah dan selisih kosinus cos + cos = 2 cos½( + ). cos½( - ) cos - cos = -2 sin½( + ). sin½( - ) 31

1. Nyatakan cos 6 x + cos 2 x sebagai bentuk perkalian. Bahasan: cos + cos = 2 cos½( + ). cos½( - ) cos 6 x + cos 2 x = 2 cos½(6 x + 2 x). cos½(6 x – 2 x) = 2 cos 5 x. cos 2 x 32

2. Nyatakan cos 160° + cos 80° sebagai bentuk perkalian. Bahasan: cos + cos = 2 cos½( + ). cos½( - ) cos 160° + cos 80° = 2 cos½(160 + 80)°. cos½(160 – 80)° = 2 cos 120°. cos 40° =2. (-½). cos 40° = -cos 40° 33

3. Bentuk Bahasan: 2 sin½(5 x + 3 x). cos½(5 x – 3 x) 2 cos½(5 x + 3 x). cos½(5 x – 3 x) sin 4 x = cos 4 x = tan 4 x 34
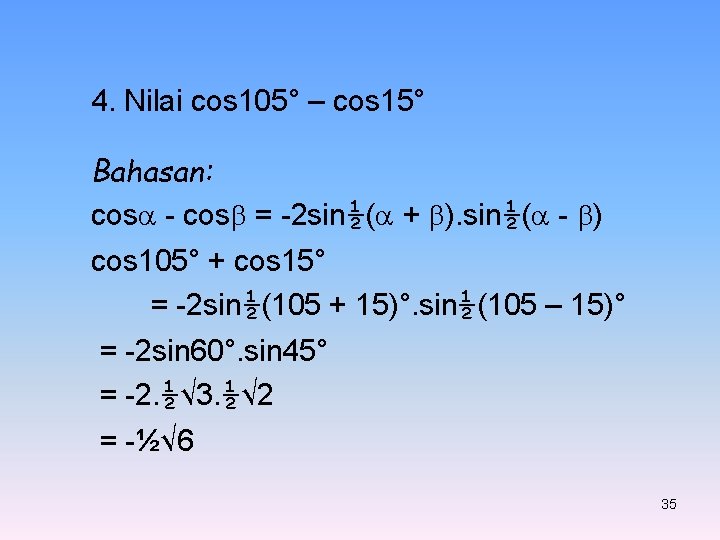
4. Nilai cos 105° – cos 15° Bahasan: cos - cos = -2 sin½( + ). sin½( - ) cos 105° + cos 15° = -2 sin½(105 + 15)°. sin½(105 – 15)° = -2 sin 60°. sin 45° = -2. ½√ 3. ½√ 2 = -½√ 6 35

5. Nilai Bahasan: -2 sin½(80 + 40). sin½(80 – 40) = sin 40° -2 sin 60°. sin 20° 2 sin 20°. cos 20° = -½√ 3 sec 20° 36

6. Nilai Bahasan: -2 sin½(4 a + 8 a). sin½(4 a – 8 a) 6 sin 6 a. sin 2 a -2 sin 6 a. sin(-2 a) = 6 sin 6 a. sin 2 a 2. sin 2 a = 6. sin 2 a =⅓ 37

SELAMAT BELAJAR 38