1 Residuals 2 Example 3 Example 4 In

1

Residuals 2

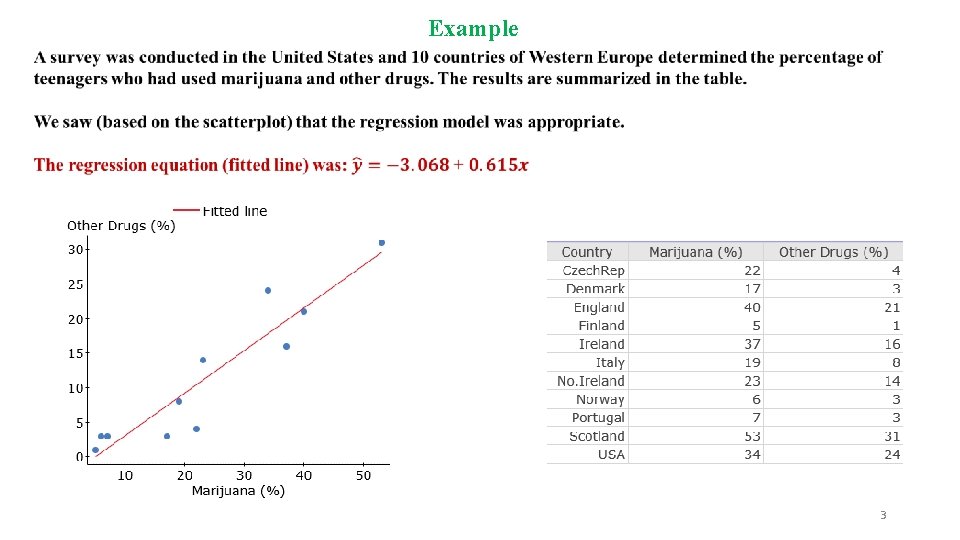
Example 3

Example 4

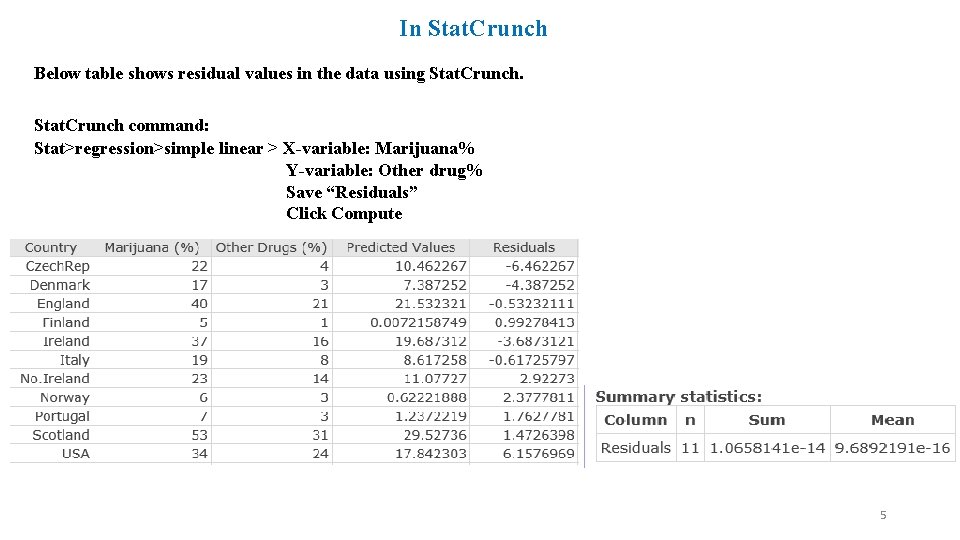
In Stat. Crunch Below table shows residual values in the data using Stat. Crunch command: Stat>regression>simple linear > X-variable: Marijuana% Y-variable: Other drug% Save “Residuals” Click Compute 5

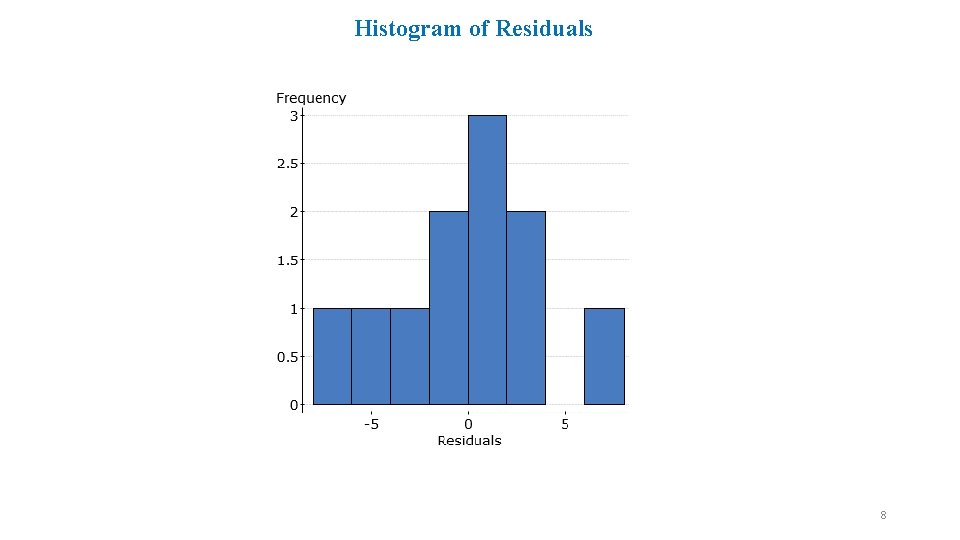
Residual Plots • Residual plots help us assess the regression model assumptions. • We check the model assumptions (assumption of random errors) using residual points. • There are three assumptions to check: 1. Residual points are approx. normally distributed (e. g. , check the normal quantile or histogram of residuals or histogram of standardized residuals). 2. Residuals have mean zero. Residual points are randomly plotted around the zero line (mean of residuals) – use the plot of residuals verses predictor or fitted value (this is a scatterplot except for here we do not want to see any obvious pattern). 3. Residuals have constant variances. Residual points are evenly spread out around the zero line - use the plot of residuals verses predictor or fitted value (this is a scatterplot except for here we do not want to see any obvious pattern like fanning: an increasing dispersion as the fitted values increase). 6

Checking the Assumptions In Stat. Crunch command: Stat>regression>simple linear > X-variable: Marijuana% Y-variable: Other drug% Graphs: Histogram of residuals QQ plot of residuals Residuals vs X-values Click Compute 7

Histogram of Residuals 8

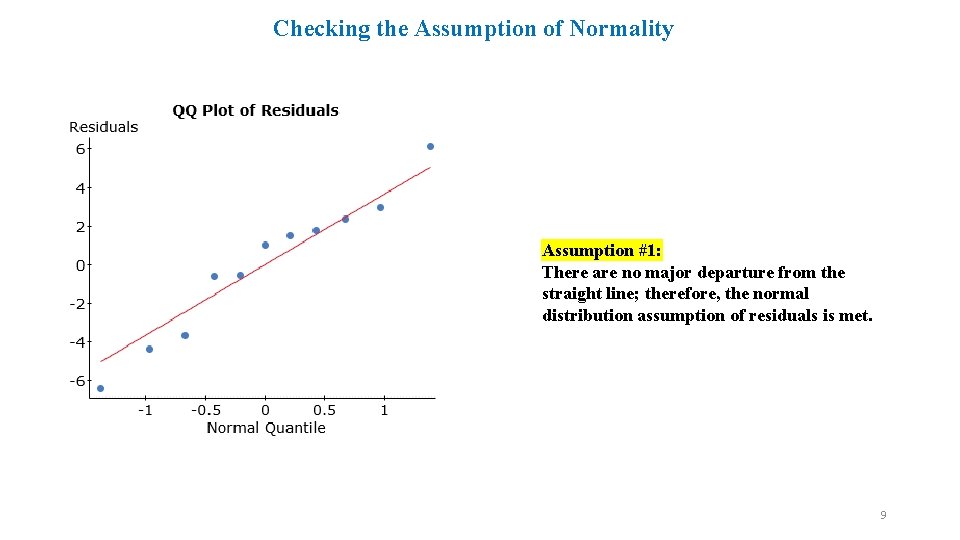
Checking the Assumption of Normality Assumption #1: There are no major departure from the straight line; therefore, the normal distribution assumption of residuals is met. 9

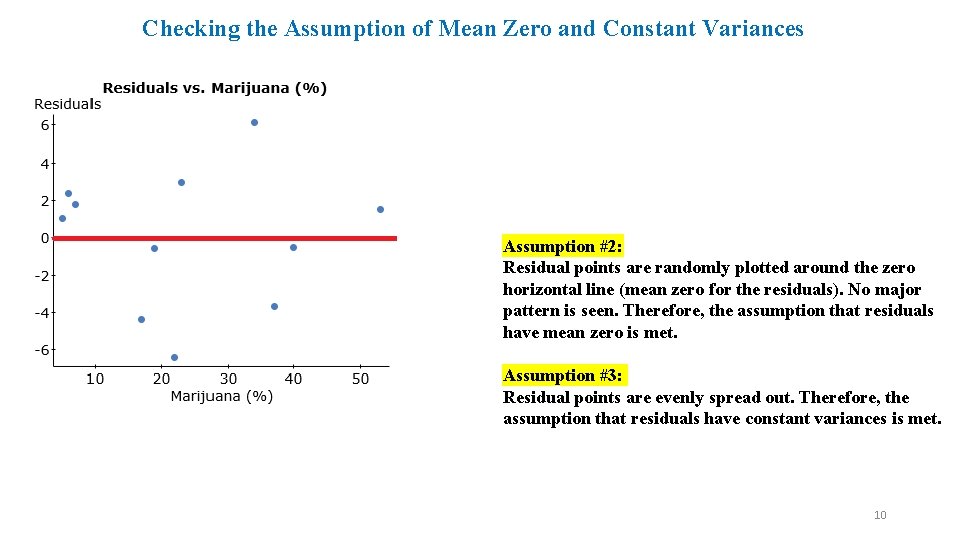
Checking the Assumption of Mean Zero and Constant Variances Assumption #2: Residual points are randomly plotted around the zero horizontal line (mean zero for the residuals). No major pattern is seen. Therefore, the assumption that residuals have mean zero is met. Assumption #3: Residual points are evenly spread out. Therefore, the assumption that residuals have constant variances is met. 10

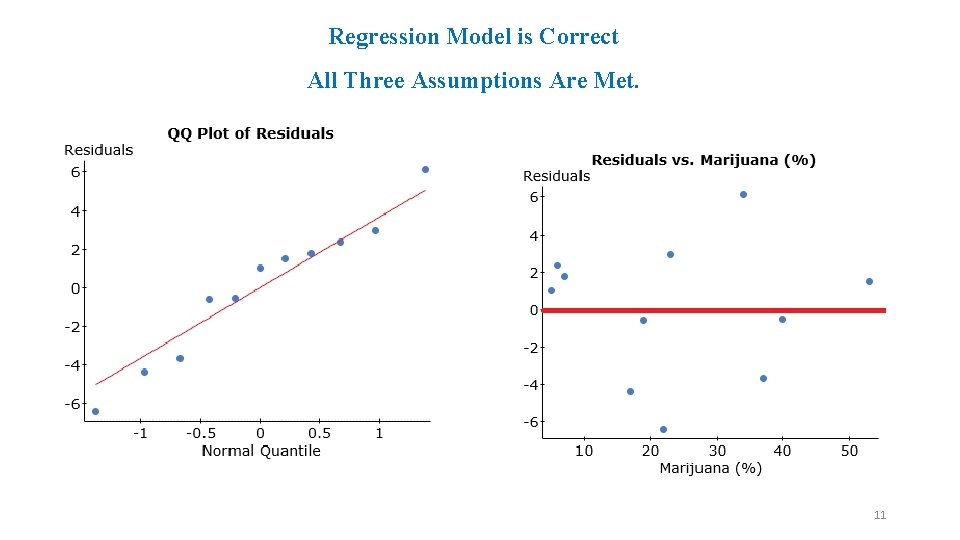
Regression Model is Correct All Three Assumptions Are Met. 11

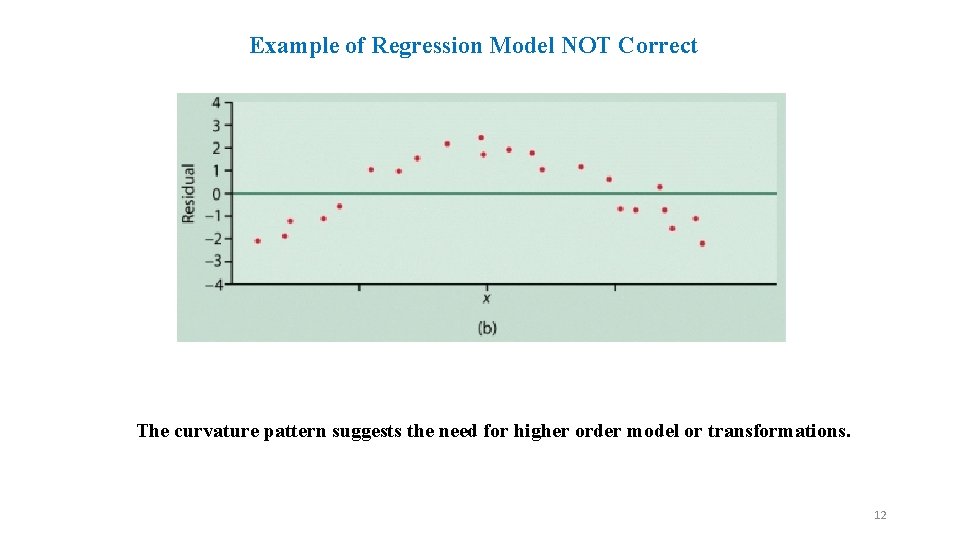
Example of Regression Model NOT Correct The curvature pattern suggests the need for higher order model or transformations. 12

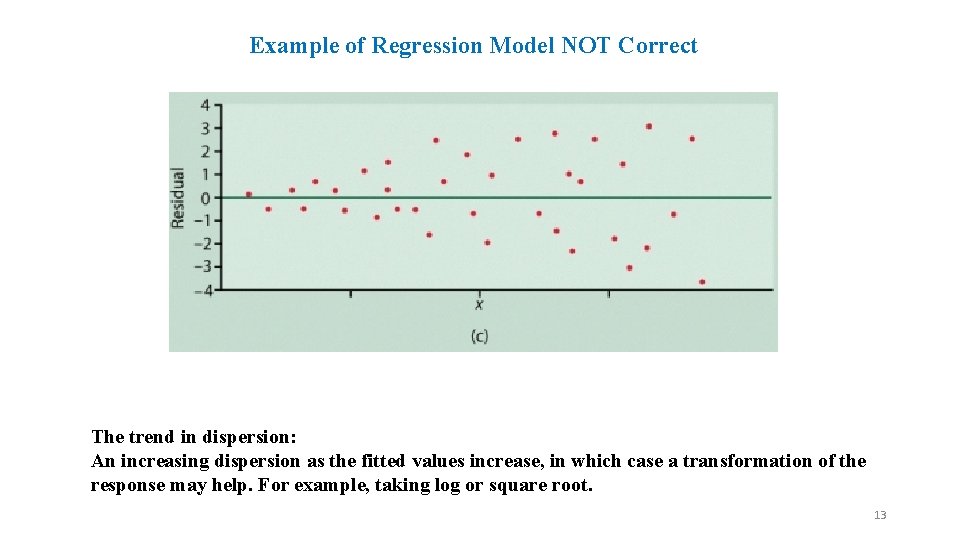
Example of Regression Model NOT Correct The trend in dispersion: An increasing dispersion as the fitted values increase, in which case a transformation of the response may help. For example, taking log or square root. 13

14

15

16

17