1 Radiation integral EMLAB Basic laws of EM

1 Radiation integral EMLAB

Basic laws of EM theory 1) Maxwell방정식 2 2) Continuity equation (전류와 전하의 관계식) 3) Constitutive relation (물질의 특성을 설명하는 식) EMLAB

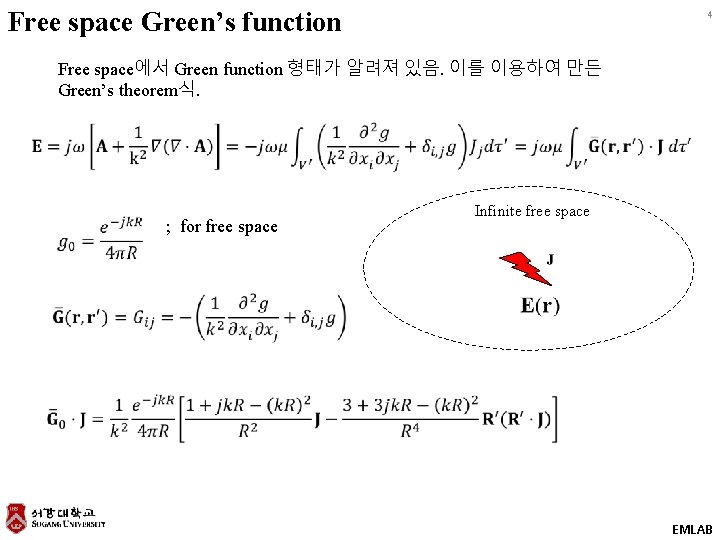
Free space Green’s function 4 Free space에서 Green function 형태가 알려져 있음. 이를 이용하여 만든 Green’s theorem식. ; for free space Infinite free space EMLAB

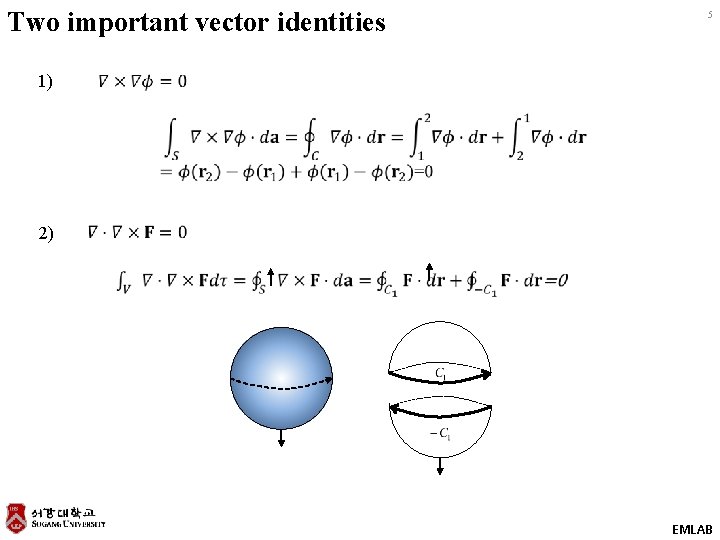
Two important vector identities 5 1) 2) EMLAB

Potentials of time-varying EM theory 6 EMLAB

Lorentz condition 7 Lorentz condition 위와 같이 divergence A를 임의로 정하면 된다. 이 경우 앞의 (3), (4)식은 아래와 같 이 간단히 된다. Lorentz condition EMLAB

Fourier transform solution 8 1. Because the number of variables are as many as four (x, y, z, t), we apply Fourier transform to the above equations. 2. For a non-homogeneous differential equation, it is easier to substitute the source term with a delta function located at origin. (effectively it is an impulse response. ) EMLAB

9 Solution of Maxwell’s eqs. for simple cases EMLAB

Infinitesimally small current element in free space : 3 D 14 Source EMLAB

Solution of wave equations in free space 15 1. As the solutions of two vector potentials are identical, scalar potential is considered first. 2. To decrease the number of independent variables (x, y, z, t), Fourier transform representation is used. 3. For convenience, a point source at origin is considered. EMLAB

Green function of free space 16 1. The solution of the differential equation with the source function substituted by a delta function is called Green g, and is first sought. 2. With a delta source, consider first the region where delta function has zero value. Then, utilize delta function to find the value of integration constant. 3. With a point source in free space, the solution has a spherical symmetry. That is, g is independent of the variables , , and is a function of r only. A suitable solution which is propagating outward from the origin is e-jkr. EMLAB

Green function of free space 17 4. To determine the value of A, apply a volume integral operation to both sides of the differential equations. The volume is a sphere with infinitesimally small radius and its center is at the origin. 5. With a source at r’, the solution is translated such that EMLAB

18 6. As the original source function can be represented by an integral of a weighted delta function, the solution to the scalar potential is also an integral of a weighted Green function. 7. Taking the inverse Fourier transform, the time domain solution is obtained as follows. EMLAB

Retarded potential 19 (Retarded potential) The distinct point from a static solution is that a time is retarded by R/c. This newly derived potential is called a retarded potential. The vector potential also contains a retarded time variable. Those A and are related to each other by Lorentz condition. EMLAB

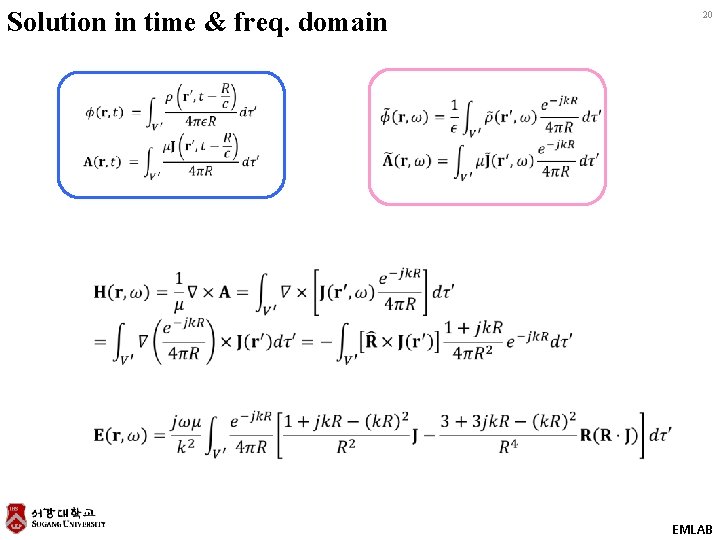
Solution in time & freq. domain 20 EMLAB

Far field approximation 21 Electrostatic solution Biot-Savart’s law Coulomb’s law EMLAB

Electric field in a phasor form 22 EMLAB

Derivation of free space dyadic Green’s function 23 EMLAB

24 R→ 인 경우 EMLAB

Radiation pattern of an infinitesimally small current 25 EMLAB

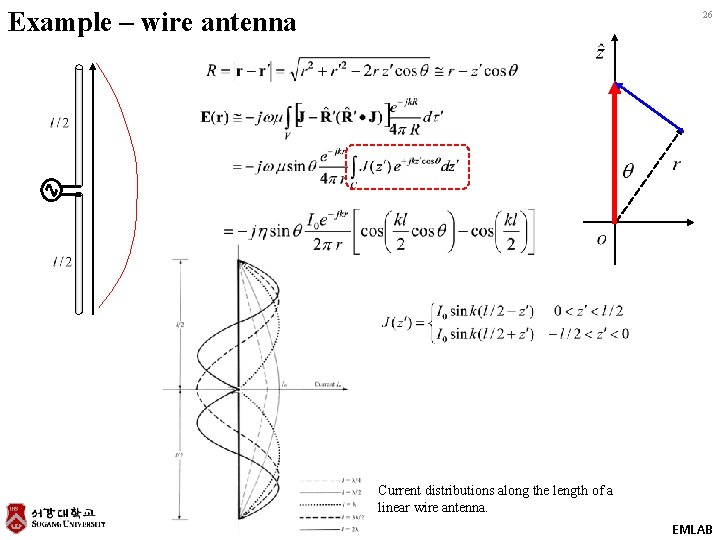
Example – wire antenna 26 Current distributions along the length of a linear wire antenna. EMLAB

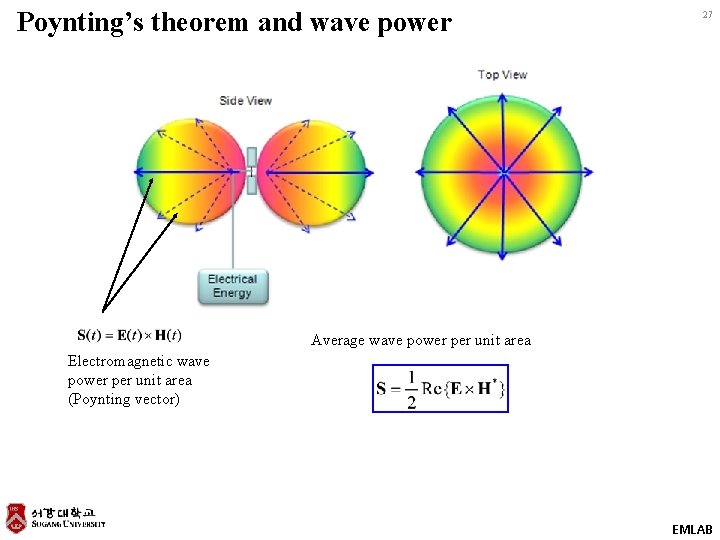
Poynting’s theorem and wave power 27 Average wave power per unit area Electromagnetic wave power per unit area (Poynting vector) EMLAB

28 EMLAB

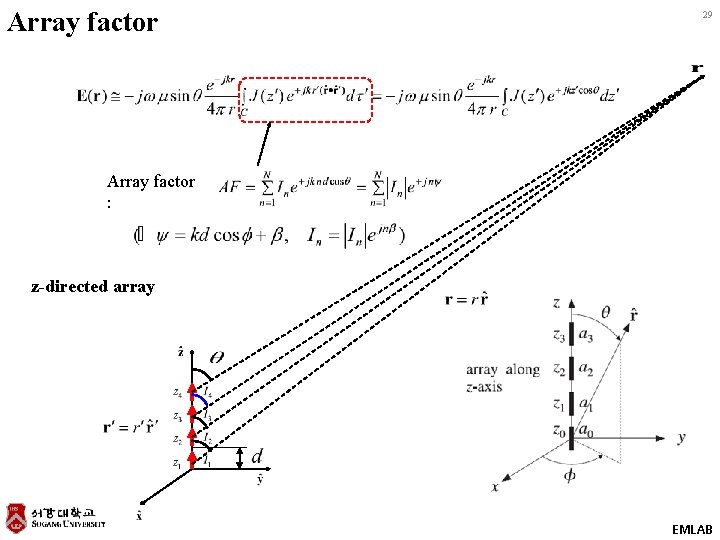
Array factor 29 Array factor : z-directed array EMLAB

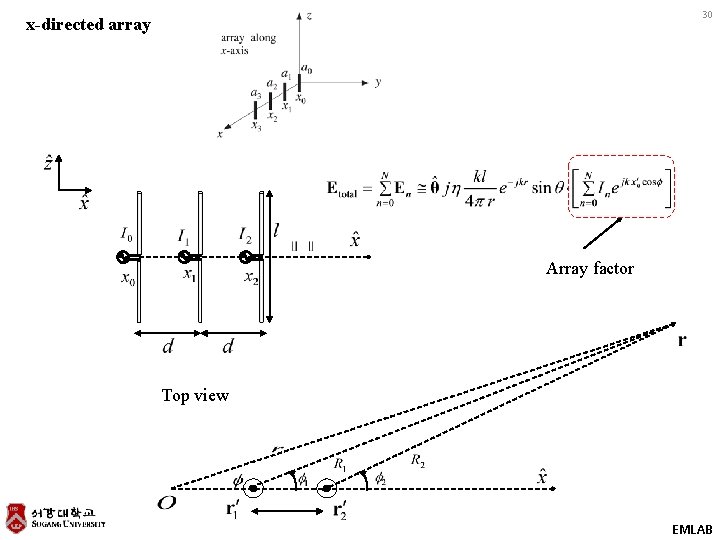
30 x-directed array Array factor Top view EMLAB

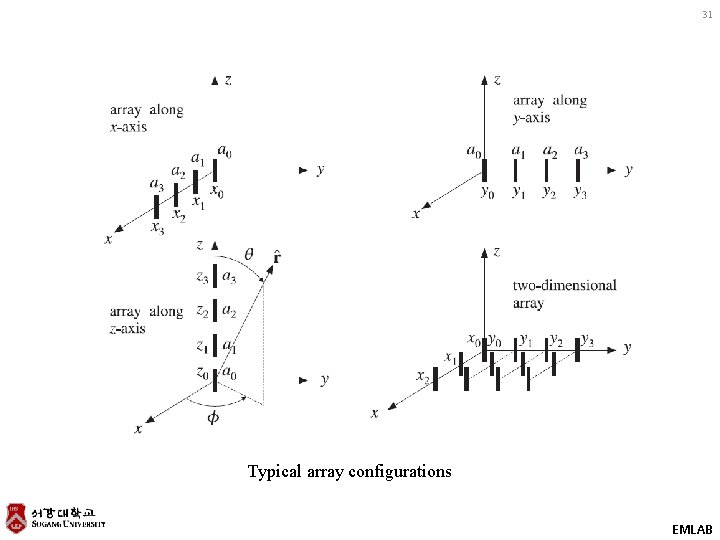
31 Typical array configurations EMLAB

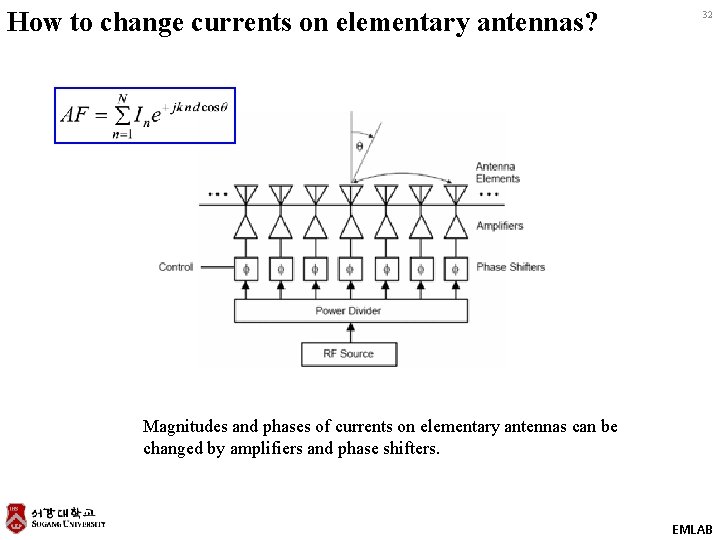
How to change currents on elementary antennas? 32 Magnitudes and phases of currents on elementary antennas can be changed by amplifiers and phase shifters. EMLAB

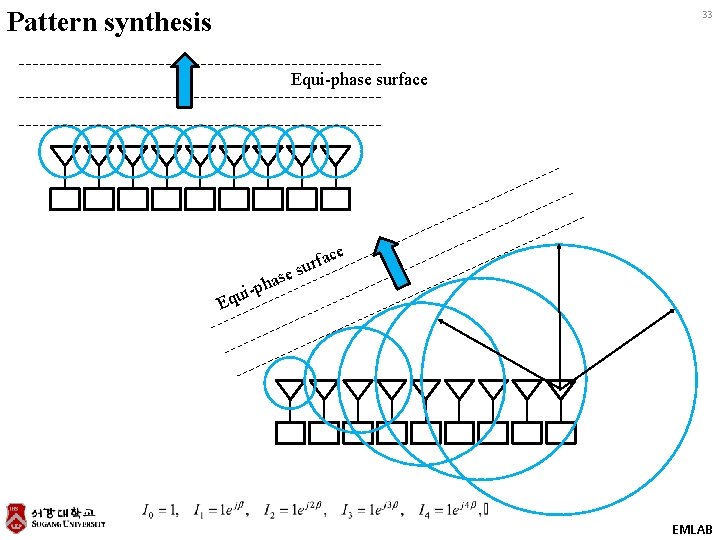
Pattern synthesis 33 Equi-phase surface se ha p i qu ce a f r su E EMLAB

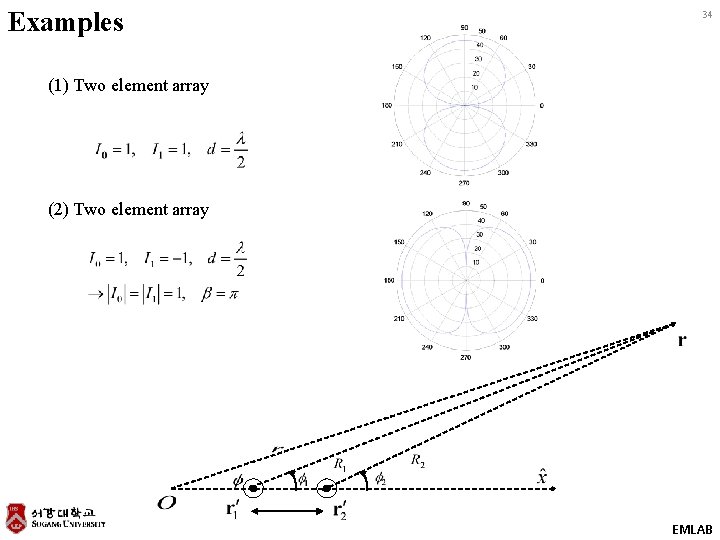
Examples 34 (1) Two element array (2) Two element array EMLAB

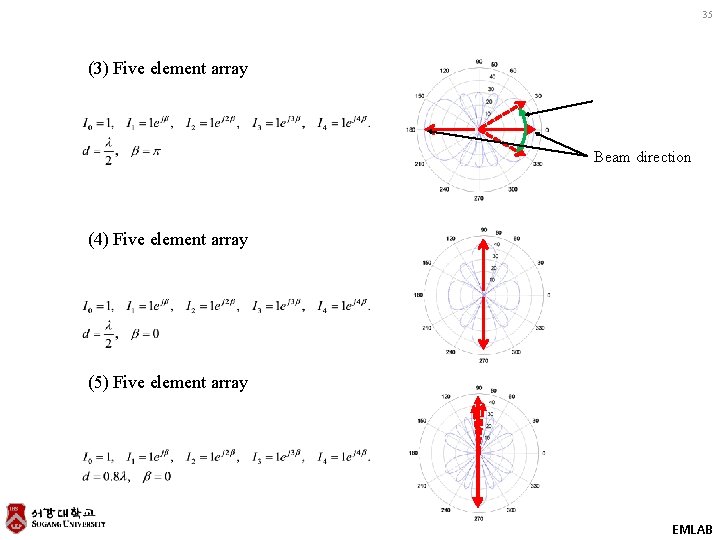
35 (3) Five element array Beam direction (4) Five element array (5) Five element array EMLAB

Sample MATLAB codes 36 phi=0: 0. 01: 2*pi; %0<phi<2*pi k=2*pi; d=0. 5; % 0. 5 lambda spacing. shi=k*d*cos(phi); alpha = pi*0. 0; beta = exp(i*alpha); %Currents=[1, 2*beta, 3*beta^2, 2*beta^3, 1*beta^4]; %Current excitations Currents=[1, 1*beta^2, 1*beta^3, 1*beta^4]; %Current excitations E=freqz(Currents, 1, shi); %E for different shi values E = DB(E)+30; % 최대값에서 30 d. B 범위까지 그림. E = (E>0. ). *E; polar(phi, E); %Generating the radiation pattern EMLAB

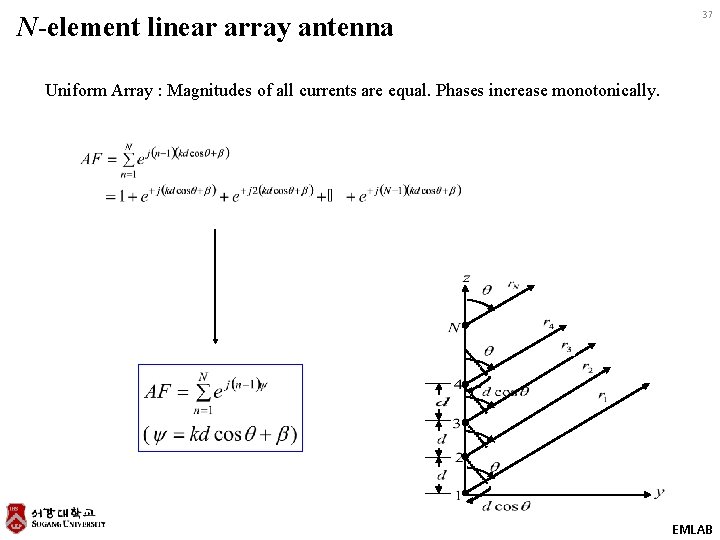
N-element linear array antenna 37 Uniform Array : Magnitudes of all currents are equal. Phases increase monotonically. EMLAB

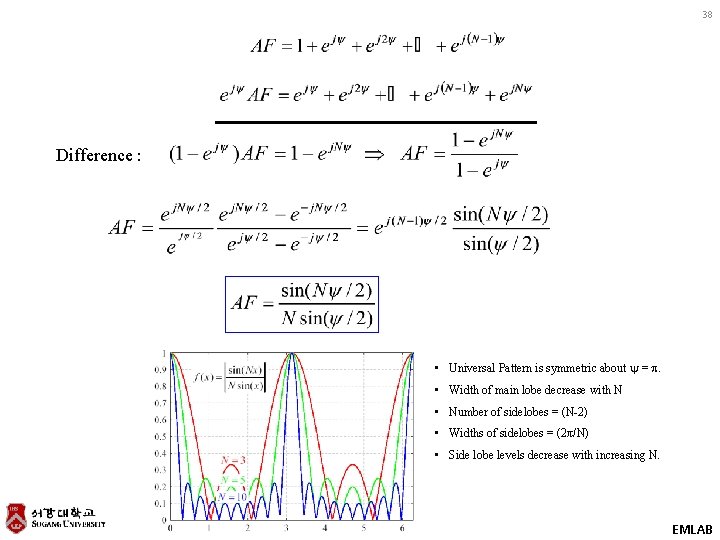
38 Difference : • Universal Pattern is symmetric about y = p. • Width of main lobe decrease with N • Number of sidelobes = (N-2) • Widths of sidelobes = (2π/N) • Side lobe levels decrease with increasing N. EMLAB

Green’s theorem 39 (Vector Green’s identity) EMLAB

40 EMLAB

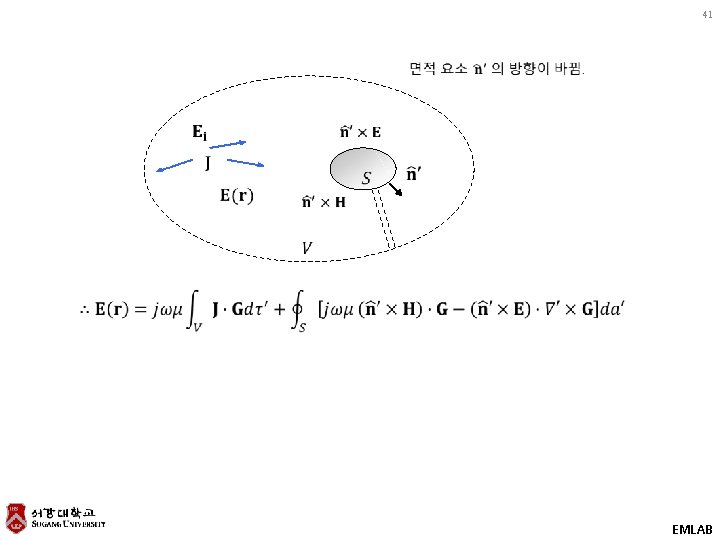
41 EMLAB

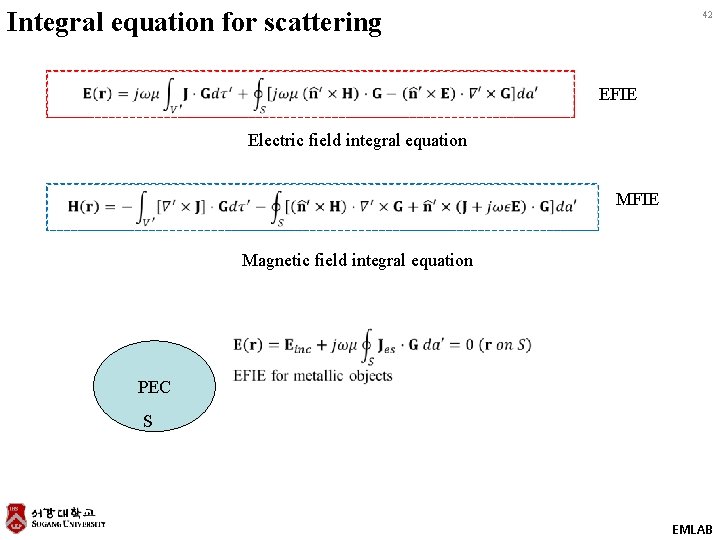
Integral equation for scattering 42 EFIE Electric field integral equation MFIE Magnetic field integral equation PEC S EMLAB

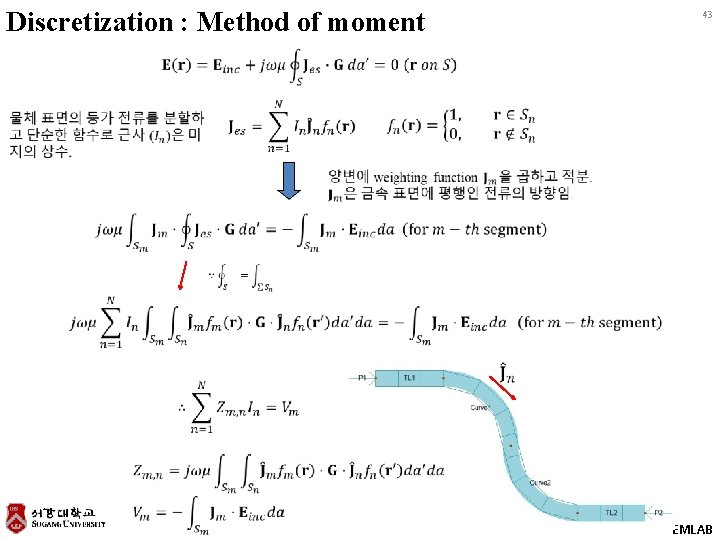
Discretization : Method of moment 43 EMLAB

Surface current discretization 44 EMLAB

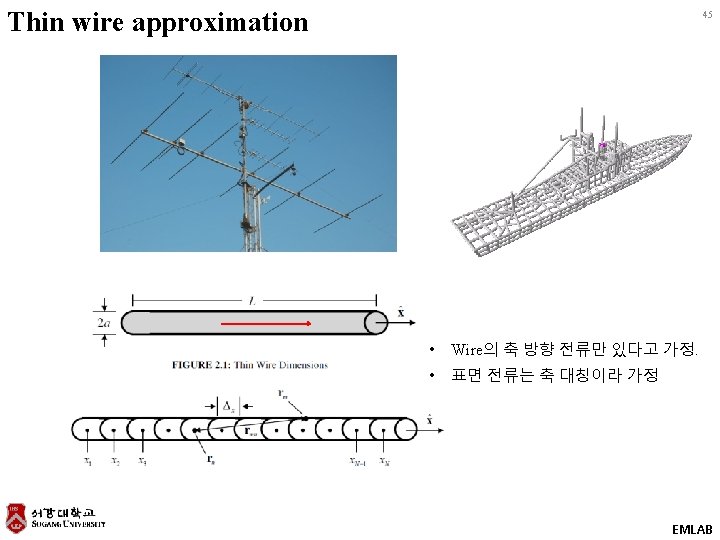
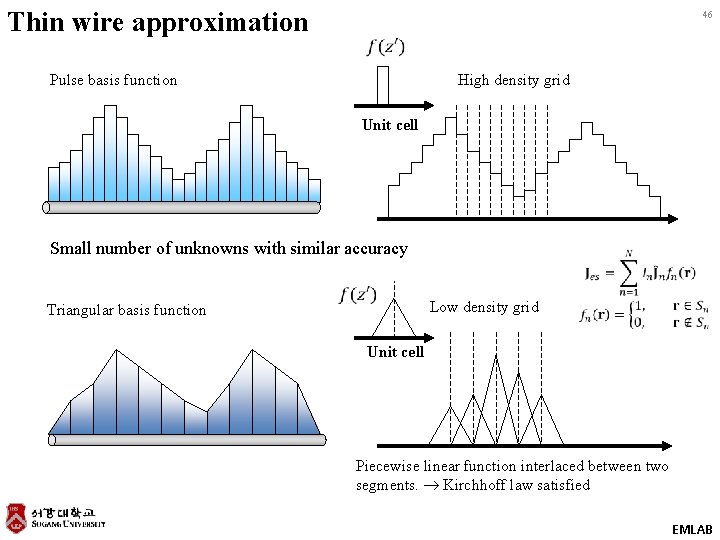
Thin wire approximation 46 Pulse basis function High density grid Unit cell Small number of unknowns with similar accuracy Triangular basis function Low density grid Unit cell Piecewise linear function interlaced between two segments. Kirchhoff law satisfied EMLAB

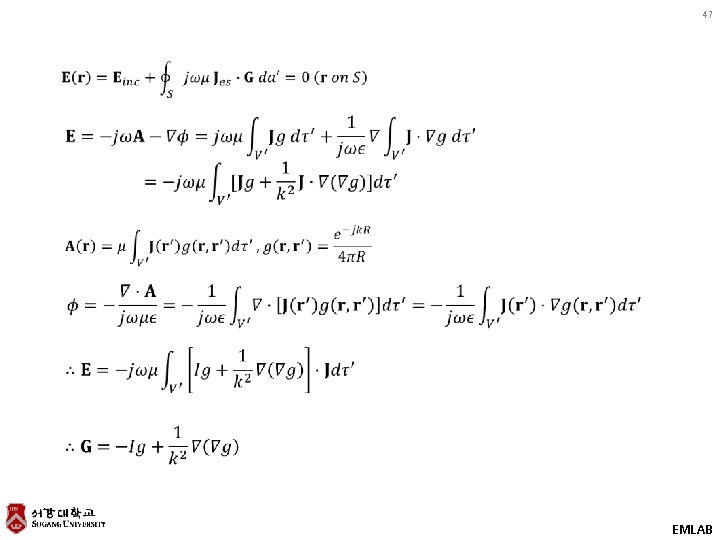
47 EMLAB

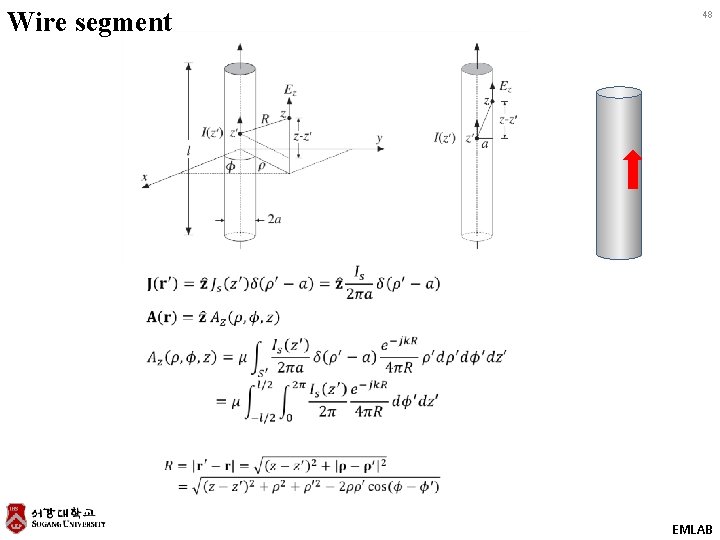
Wire segment 48 EMLAB

Thin wire antenna approximation 49 E-field by a z-axis directed linear antenna EMLAB

50 Pocklington’s integral equation Hallen’s integral equation Constraint : EMLAB

Pocklington’s Equation 51 EMLAB

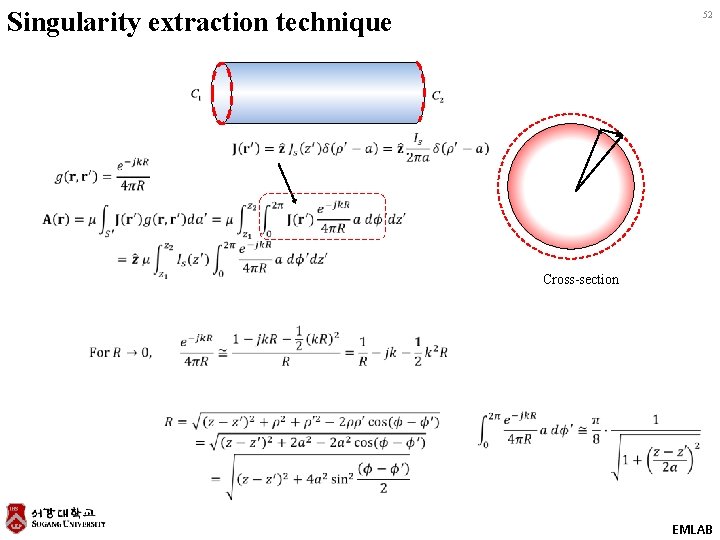
Singularity extraction technique 52 Cross-section EMLAB

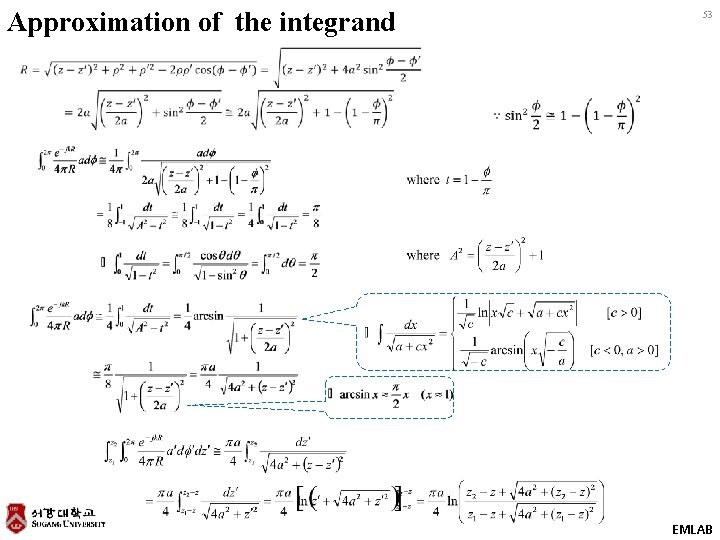
Approximation of the integrand 53 EMLAB

Mixed potential formulation (Harrington’s) 54 Thin wire approximation EMLAB

55 With pulse basis function, EMLAB

EFIE for thick wire 56 EMLAB

Mo. M impedance matrix 57 EMLAB

Impedance matrix : pulse basis functions 58 For pulse basis functions EMLAB

59 For thin wire antenna Self term : Distant term : EMLAB

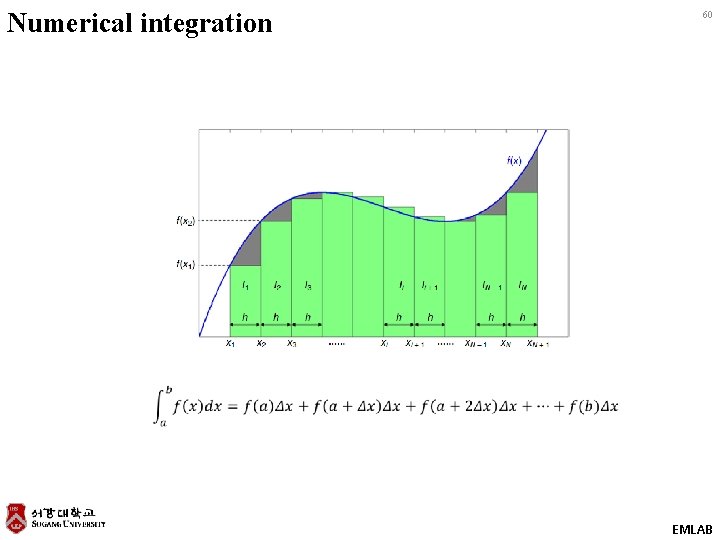
Numerical integration 60 EMLAB

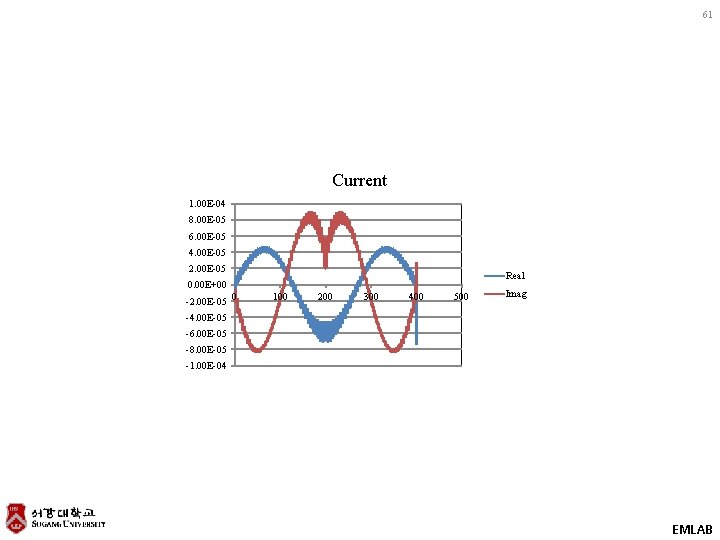
61 Current 1. 00 E-04 8. 00 E-05 6. 00 E-05 4. 00 E-05 2. 00 E-05 Real 0. 00 E+00 -2. 00 E-05 0 100 200 300 400 500 Imag -4. 00 E-05 -6. 00 E-05 -8. 00 E-05 -1. 00 E-04 EMLAB

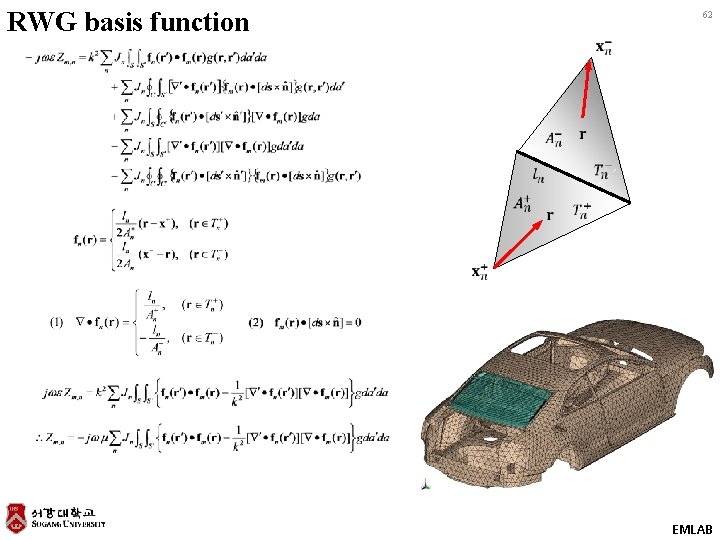
RWG basis function 62 EMLAB

63 EMLAB

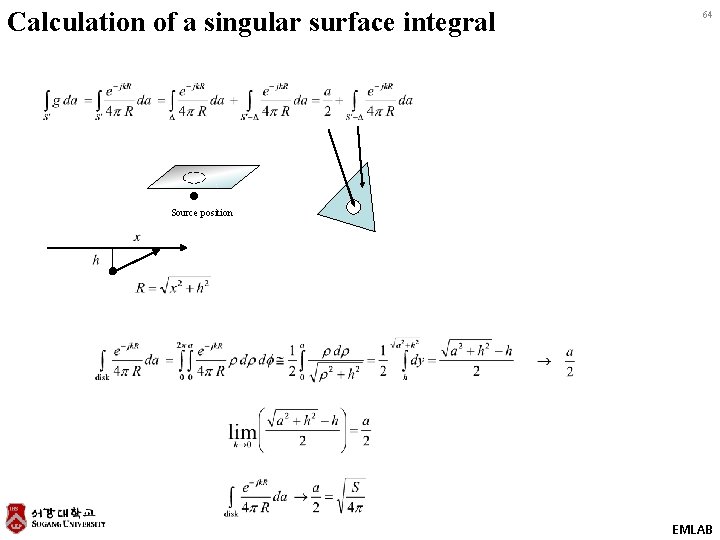
Calculation of a singular surface integral 64 Source position EMLAB

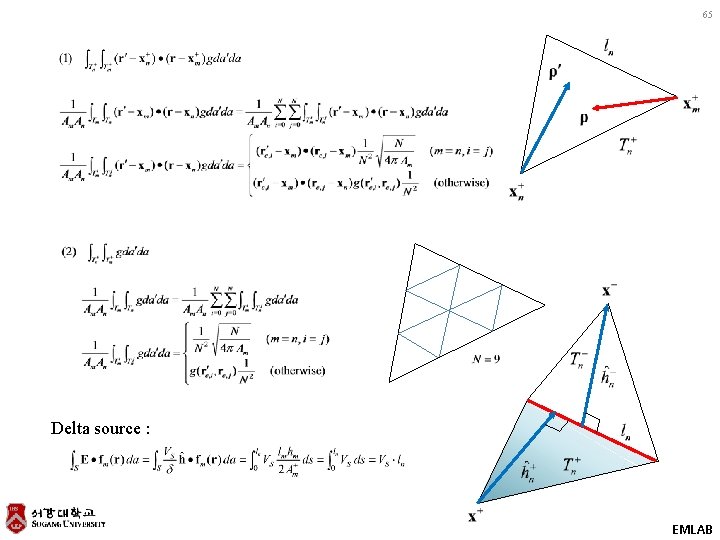
65 Delta source : EMLAB