1 Queues Lecture 4 2 Lecture Objectives In

1 Queues Lecture 4

2 Lecture Objectives In this lecture, you will: Ø Learn about queues Ø Examine various queue operations Ø Learn how to implement a queue as an array Ø Learn how to implement a queue as a linked list Ø Examine the STL class queue Ø Discover queue applications Ø Learn about priority queue Ø Examine the STL class priority_queue

Queues 3 ØThe notion of a queue in computer science is the same as the notion of the queues to which you are accustomed in everyday life. ØExamples: 1 – There are queues of customers in a bank. 2 – There are queues of customers in a grocery store. 3 – There are queues of cars waiting to pass through a tollbooth. 4 - Similarly, because a computer can send a print request faster than a printer can print, a queue of documents is often waiting to be printed at a printer.

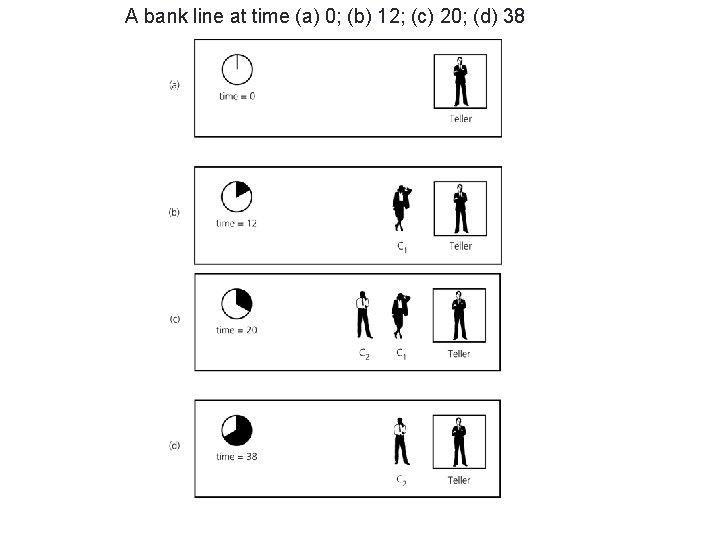
A bank line at time (a) 0; (b) 12; (c) 20; (d) 38 4

5 Queues ØDefinition: A queue is a set of elements of the same type in which the elements are added at one end, called the back or rear, and deleted from the other end, called the front or first ØFirst In First Out (FIFO) data structure

6 FIFO First In First Out (FIFO) data structure The general rule to process elements in a queue is that the customer at the front of the queue is served next and that when a new customer arrives, he or she stands at the end of the queue. That is, a queue is a First In First Out, or simply FIFO data structure.

7 ADT Queue Operations 1. Create an empty queue. 2. Destroy a queue. 3. Determine whether a queue is empty. 4. Add a new item to the queue. 5. Remove from the queue the item that was added earliest. 6. Retrieve from the queue the item that was added earliest.

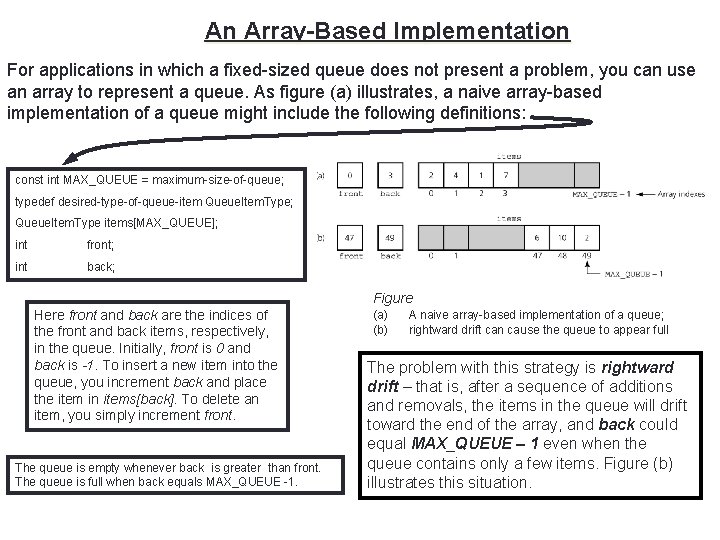
An Array-Based Implementation 8 For applications in which a fixed-sized queue does not present a problem, you can use an array to represent a queue. As figure (a) illustrates, a naive array-based implementation of a queue might include the following definitions: const int MAX_QUEUE = maximum-size-of-queue; typedef desired-type-of-queue-item Queue. Item. Type; Queue. Item. Type items[MAX_QUEUE]; int front; int back; Figure Here front and back are the indices of the front and back items, respectively, in the queue. Initially, front is 0 and back is -1. To insert a new item into the queue, you increment back and place the item in items[back]. To delete an item, you simply increment front. The queue is empty whenever back is greater than front. The queue is full when back equals MAX_QUEUE -1. (a) (b) A naive array-based implementation of a queue; rightward drift can cause the queue to appear full The problem with this strategy is rightward drift – that is, after a sequence of additions and removals, the items in the queue will drift toward the end of the array, and back could equal MAX_QUEUE – 1 even when the queue contains only a few items. Figure (b) illustrates this situation.

9 An Array-Based Implementation One possible solution to this problem is to shift array elements to the left, either after each deletion or whenever back equals MAX_QUEUE – 1. This solution guarantees that the queue can always contain up to MAX_QUEUE items. Shifting is not really satisfactory, however, as it would dominate the cost of the implementation.

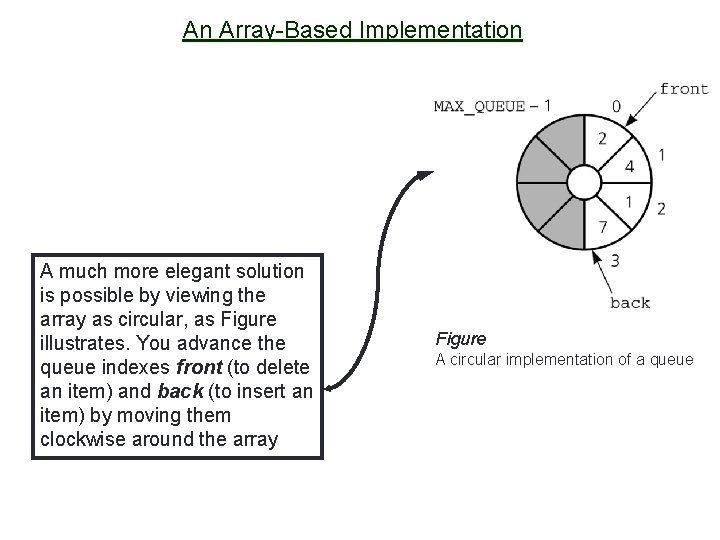
An Array-Based Implementation A much more elegant solution is possible by viewing the array as circular, as Figure illustrates. You advance the queue indexes front (to delete an item) and back (to insert an item) by moving them clockwise around the array 10 Figure A circular implementation of a queue

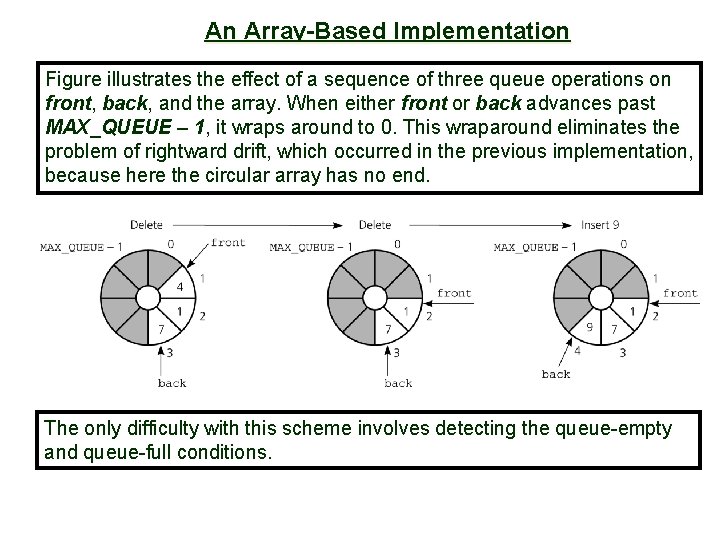
An Array-Based Implementation 11 Figure illustrates the effect of a sequence of three queue operations on front, back, and the array. When either front or back advances past MAX_QUEUE – 1, it wraps around to 0. This wraparound eliminates the problem of rightward drift, which occurred in the previous implementation, because here the circular array has no end. The only difficulty with this scheme involves detecting the queue-empty and queue-full conditions.

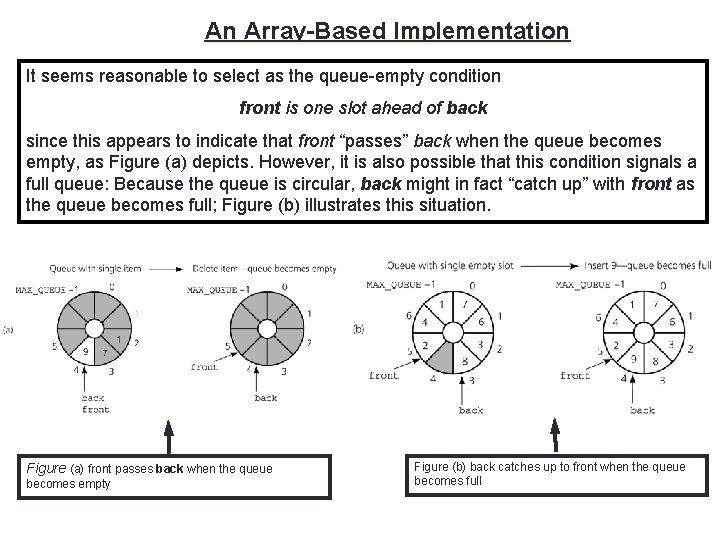
An Array-Based Implementation 12 It seems reasonable to select as the queue-empty condition front is one slot ahead of back since this appears to indicate that front “passes” back when the queue becomes empty, as Figure (a) depicts. However, it is also possible that this condition signals a full queue: Because the queue is circular, back might in fact “catch up” with front as the queue becomes full; Figure (b) illustrates this situation. Figure (a) front passes back when the queue becomes empty Figure (b) back catches up to front when the queue becomes full

An Array-Based Implementation 13 Obviously, you need a way to distinguish between the two situations. One such way is to keep a count of the number of items in the queue. => Before inserting into the queue, you check to see if the count is equal to MAX_QUEUE: if it is, the queue is full. => Before deleting an item from the queue, you check to see if the count is zero; if it is, the queue is empty.

An Array-Based Implementation 14 To initialize the queue, you set front to 0, back to MAX_QUEUE – 1, and count to 0. You obtain the wraparound effect of a circular queue by using modulo arithmetic (that is, the C++ % operator) when incrementing front and back. For example, example you can insert new. Item into the queue by using the statements back = (back+1) % MAX_QUEUE; items[back] = new. Item; ++count; Notice that if back equaled MAX_QUEUE -1 before the insertion of new. Item, the first statement, back = (back+1) % MAX_QUEUE, would have the effect of wrapping back around to location 0. Similarly, you can delete the item at the front of the queue by using the statements front = (front+1) % MAX_QUEUE; --count;

An Array-Based Implementation 15 Sometimes you do not require a count of the number of items in the queue. One approach uses a flag is. Full to distinguish between the full and empty conditions. The expense of maintaining an is. Full flag is about the same as that of maintaining a counter. However, a faster implementation declares MAX_QUEUE + 1 locations for the array items, but uses only MAX_QUEUE of them for queue items. You sacrifice one array location and make front the index of the location before the front of the queue.

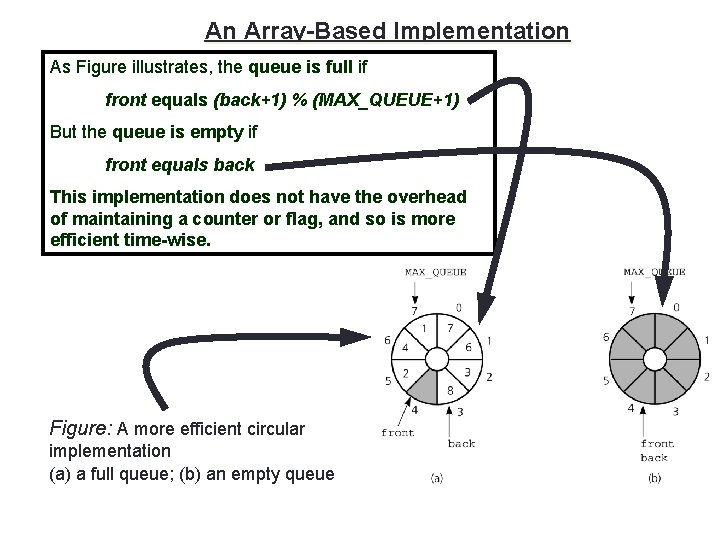
An Array-Based Implementation As Figure illustrates, the queue is full if front equals (back+1) % (MAX_QUEUE+1) But the queue is empty if front equals back This implementation does not have the overhead of maintaining a counter or flag, and so is more efficient time-wise. Figure: A more efficient circular implementation (a) a full queue; (b) an empty queue 16

17 An Array-Based Implementation of the ADT Queue

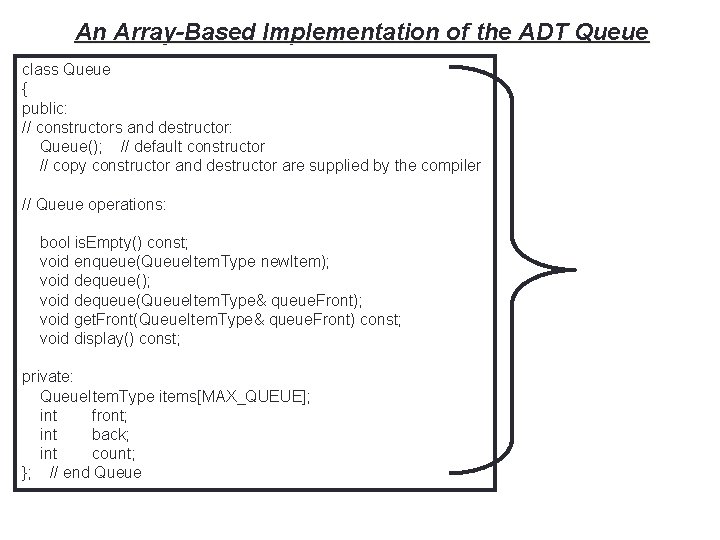
18 An Array-Based Implementation of the ADT Queue class Queue { public: // constructors and destructor: Queue(); // default constructor // copy constructor and destructor are supplied by the compiler // Queue operations: bool is. Empty() const; void enqueue(Queue. Item. Type new. Item); void dequeue(Queue. Item. Type& queue. Front); void get. Front(Queue. Item. Type& queue. Front) const; void display() const; private: Queue. Item. Type items[MAX_QUEUE]; int front; int back; int count; }; // end Queue class Declaration of class Queue

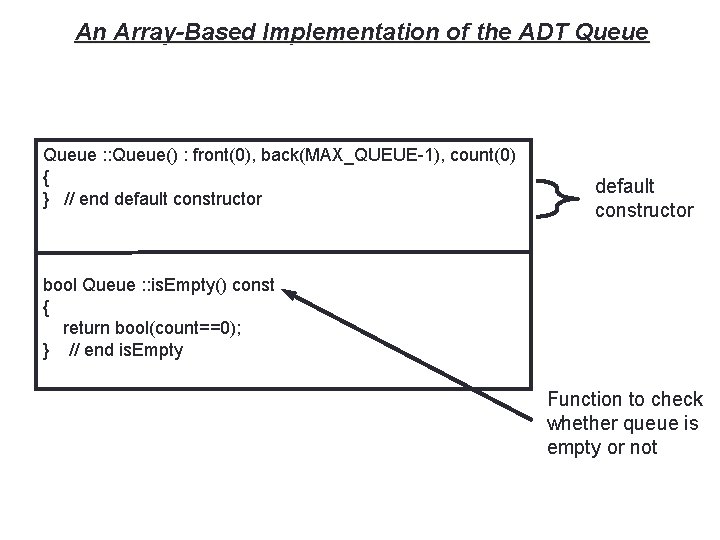
19 An Array-Based Implementation of the ADT Queue : : Queue() : front(0), back(MAX_QUEUE-1), count(0) { } // end default constructor bool Queue : : is. Empty() const { return bool(count==0); } // end is. Empty Function to check whether queue is empty or not

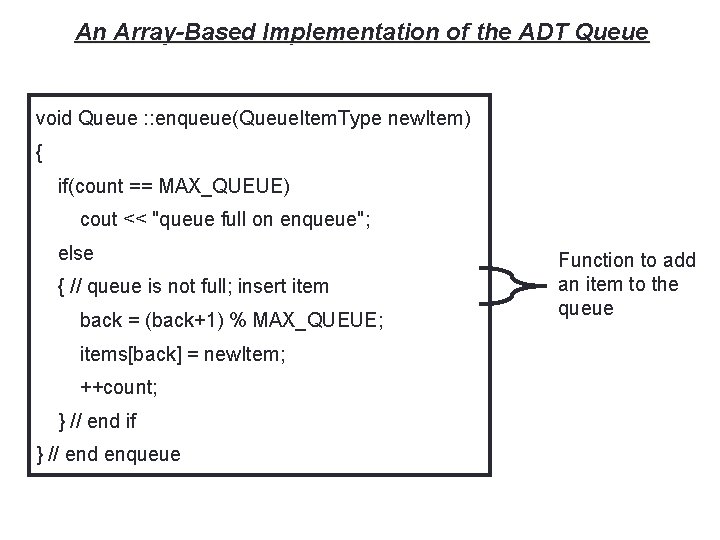
20 An Array-Based Implementation of the ADT Queue void Queue : : enqueue(Queue. Item. Type new. Item) { if(count == MAX_QUEUE) cout << "queue full on enqueue"; else { // queue is not full; insert item back = (back+1) % MAX_QUEUE; items[back] = new. Item; ++count; } // end if } // end enqueue Function to add an item to the queue

21 An Array-Based Implementation of the ADT Queue void Queue : : dequeue() { if (is. Empty()) cout << "empty queue, cannot dequeue" ; else { // queue is not empty; remove front = (front+1) % MAX_QUEUE; --count; } // end if } // end dequeue Function to remove front item from the queue

22 An Array-Based Implementation of the ADT Queue void Queue : : dequeue(Queue. Item. Type& queue. Front) { if (is. Empty()) cout << "empty queue, cannot dequeuen" ; else { // queue is not empty; retrieve and remove front queue. Front = items[front]; front = (front+1) % MAX_QUEUE; --count; cout << "Front element of the queue is “; cout << queue. Front << endl; } // end if } // end dequeue Function to retrieve and remove front item from the queue

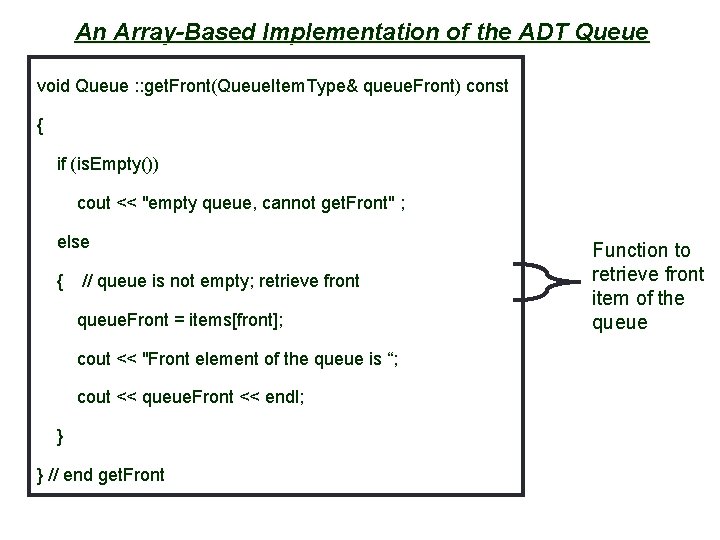
23 An Array-Based Implementation of the ADT Queue void Queue : : get. Front(Queue. Item. Type& queue. Front) const { if (is. Empty()) cout << "empty queue, cannot get. Front" ; else { // queue is not empty; retrieve front queue. Front = items[front]; cout << "Front element of the queue is “; cout << queue. Front << endl; } } // end get. Front Function to retrieve front item of the queue

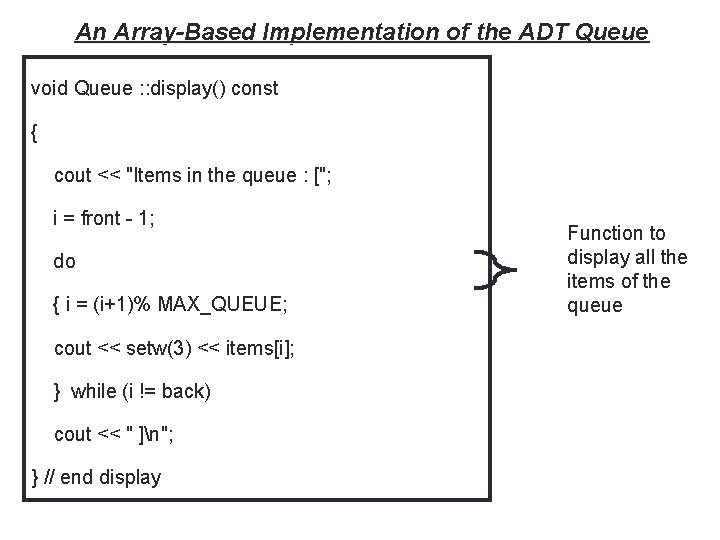
24 An Array-Based Implementation of the ADT Queue void Queue : : display() const { cout << "Items in the queue : ["; i = front - 1; do { i = (i+1)% MAX_QUEUE; cout << setw(3) << items[i]; } while (i != back) cout << " ]n"; } // end display Function to display all the items of the queue

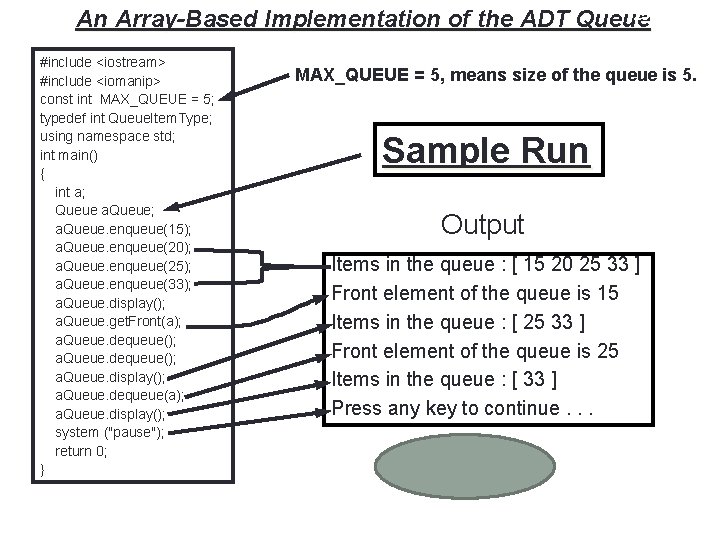
25 An Array-Based Implementation of the ADT Queue #include <iostream> #include <iomanip> const int MAX_QUEUE = 5; typedef int Queue. Item. Type; using namespace std; int main() { int a; Queue a. Queue; a. Queue. enqueue(15); a. Queue. enqueue(20); a. Queue. enqueue(25); a. Queue. enqueue(33); a. Queue. display(); a. Queue. get. Front(a); a. Queue. dequeue(); a. Queue. display(); a. Queue. dequeue(a); a. Queue. display(); system ("pause"); return 0; } MAX_QUEUE = 5, means size of the queue is 5. Sample Run Output Items in the queue : [ 15 20 25 33 ] Front element of the queue is 15 Items in the queue : [ 25 33 ] Front element of the queue is 25 Items in the queue : [ 33 ] Press any key to continue. . .

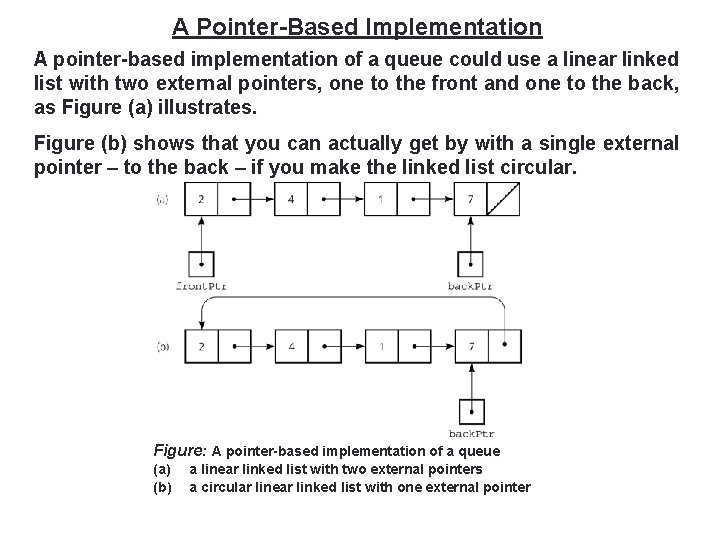
A Pointer-Based Implementation 26 A pointer-based implementation of a queue could use a linear linked list with two external pointers, one to the front and one to the back, as Figure (a) illustrates. Figure (b) shows that you can actually get by with a single external pointer – to the back – if you make the linked list circular. Figure: A pointer-based implementation of a queue (a) (b) a linear linked list with two external pointers a circular linear linked list with one external pointer

A Pointer-Based Implementation 27 Insertion at the back and deletion from the front are straightforward. Figure illustrates the addition of an item to a nonempty queue. Inserting the new node, to which new. Ptr points, at the back of the queue requires three pointer changes: the next pointer in the new node, the next pointer in the current back node, and the external pointer back. Ptr. Figure depicts these changes and indicates the order in which they can occur. (The dashed lines indicate pointer values before the changes. ) Figure: Inserting an item into a nonempty queue

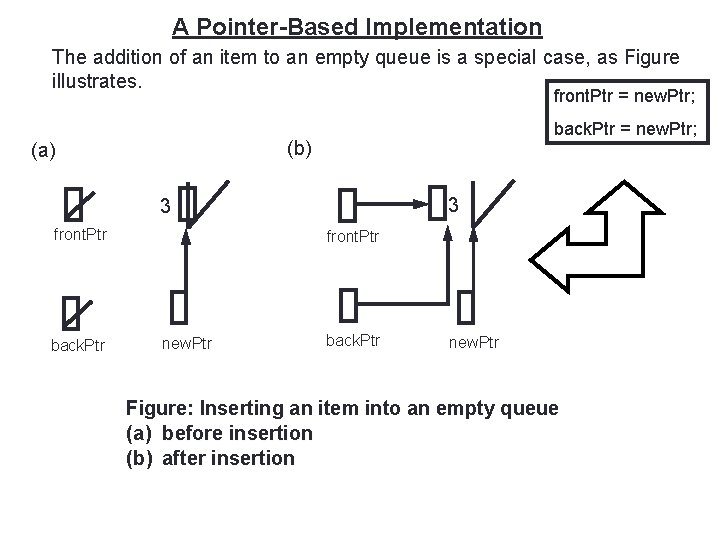
28 A Pointer-Based Implementation The addition of an item to an empty queue is a special case, as Figure illustrates. front. Ptr = new. Ptr; back. Ptr = new. Ptr; (b) (a) 3 3 front. Ptr back. Ptr front. Ptr new. Ptr back. Ptr new. Ptr Figure: Inserting an item into an empty queue (a) before insertion (b) after insertion

A Pointer-Based Implementation 29 Deletion from the front of the queue is simpler than insertion at the back. Figure illustrates the removal of the front item of a queue that contains more than one item. Notice that you need to change only the external pointer front. Ptr. Deletion from a queue of one item is a special case that sets the external pointers back. Ptr and front. Ptr to NULL. Figure: Deleting an item from a queue of more than one item

30 A Pointer-Based Implementation of the ADT Queue (linked queue)

31 A Pointer-Based Implementation of the ADT Queue class Queue { public: // constructors and destructor: Queue(); // default constructor Queue(const Queue& Q); // copy constructor ~Queue(); // destructor // Queue operations: bool is. Empty() const; // Determines whether the queue is empty. // Precondition: None. // Postcondition: Returns true if the queue is empty, otherwise returns false. void enqueue(Queue. Item. Type new. Item); // Inserts an item at the back of a queue. // Precondition: new. Item is the item to be inserted. // Postcondition: If the insertion is successful, new. Item is at the back of the queue.

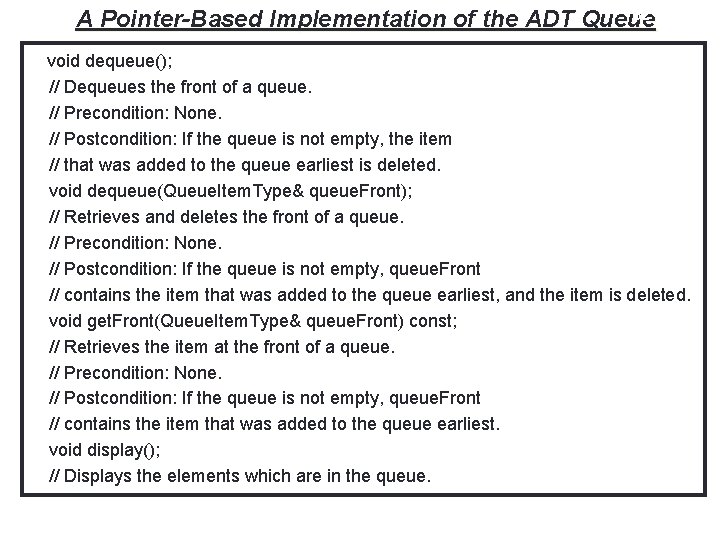
32 A Pointer-Based Implementation of the ADT Queue void dequeue(); // Dequeues the front of a queue. // Precondition: None. // Postcondition: If the queue is not empty, the item // that was added to the queue earliest is deleted. void dequeue(Queue. Item. Type& queue. Front); // Retrieves and deletes the front of a queue. // Precondition: None. // Postcondition: If the queue is not empty, queue. Front // contains the item that was added to the queue earliest, and the item is deleted. void get. Front(Queue. Item. Type& queue. Front) const; // Retrieves the item at the front of a queue. // Precondition: None. // Postcondition: If the queue is not empty, queue. Front // contains the item that was added to the queue earliest. void display(); // Displays the elements which are in the queue.

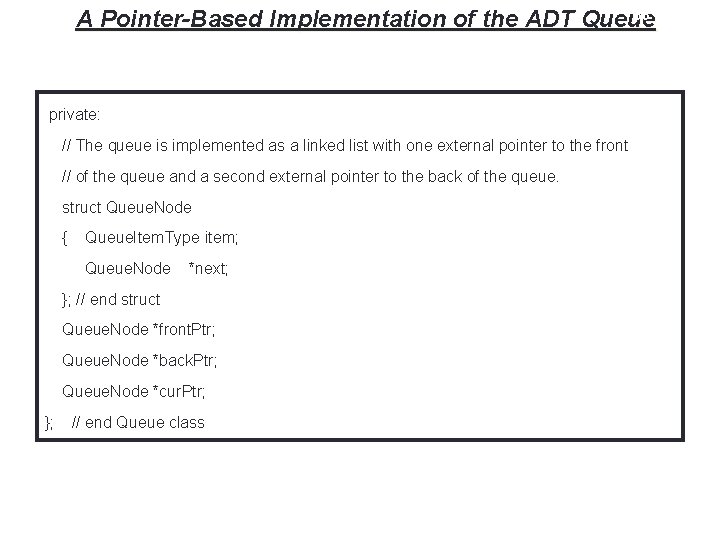
33 A Pointer-Based Implementation of the ADT Queue private: // The queue is implemented as a linked list with one external pointer to the front // of the queue and a second external pointer to the back of the queue. struct Queue. Node { Queue. Item. Type item; Queue. Node *next; }; // end struct Queue. Node *front. Ptr; Queue. Node *back. Ptr; Queue. Node *cur. Ptr; }; // end Queue class

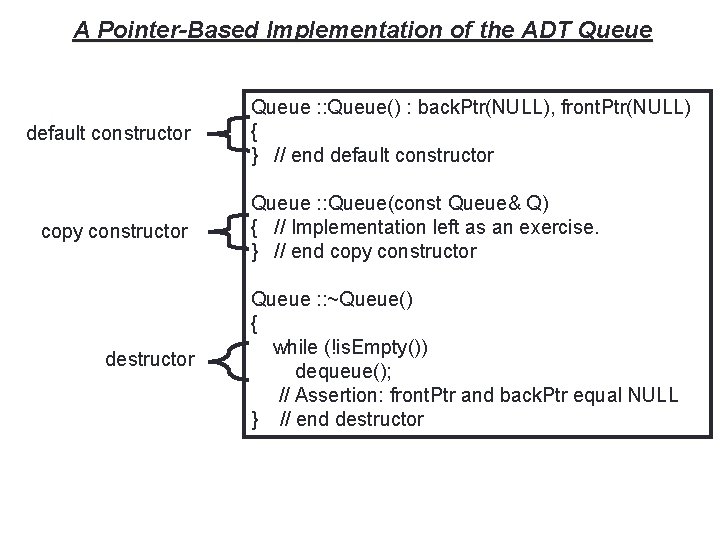
34 A Pointer-Based Implementation of the ADT Queue default constructor copy constructor destructor Queue : : Queue() : back. Ptr(NULL), front. Ptr(NULL) { } // end default constructor Queue : : Queue(const Queue& Q) { // Implementation left as an exercise. } // end copy constructor Queue : : ~Queue() { while (!is. Empty()) dequeue(); // Assertion: front. Ptr and back. Ptr equal NULL } // end destructor

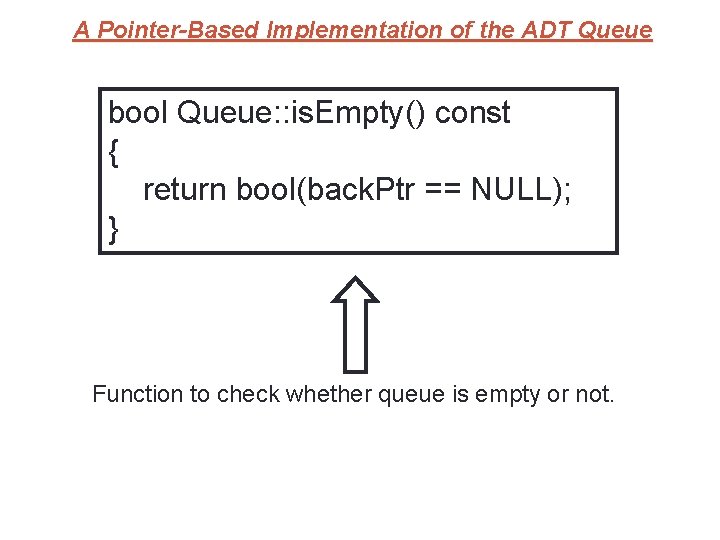
35 A Pointer-Based Implementation of the ADT Queue bool Queue: : is. Empty() const { return bool(back. Ptr == NULL); } // end is. Empty Function to check whether queue is empty or not.

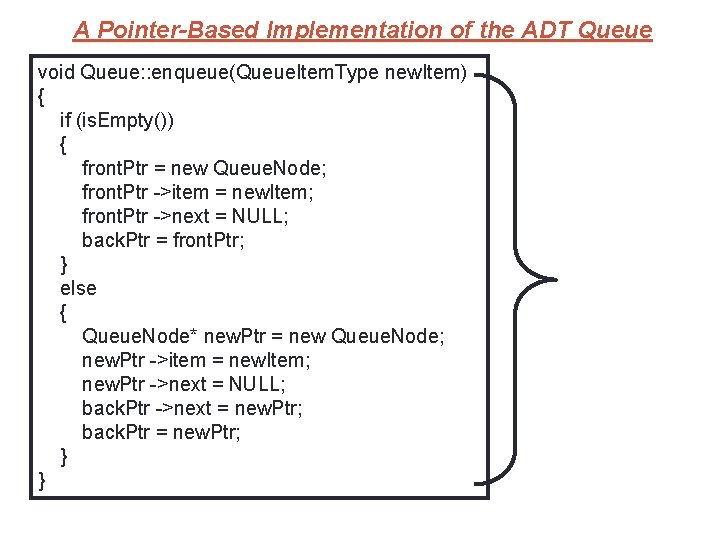
36 A Pointer-Based Implementation of the ADT Queue void Queue: : enqueue(Queue. Item. Type new. Item) { if (is. Empty()) { front. Ptr = new Queue. Node; front. Ptr ->item = new. Item; front. Ptr ->next = NULL; back. Ptr = front. Ptr; } else { // create a new node Queue. Node* new. Ptr = new Queue. Node; new. Ptr ->item = new. Item; new. Ptr ->next = NULL; back. Ptr ->next = new. Ptr; back. Ptr = new. Ptr; } } // end enqueue Function to add an item to the queue

37 A Pointer-Based Implementation of the ADT Queue void Queue : : dequeue() { if (is. Empty()) cout << "empty queue, cannot dequeue" ; else { // queue is not empty; remove front Queue. Node *temp. Ptr = front. Ptr; if (front. Ptr == back. Ptr) // special case? { // yes, one node in queue front. Ptr = NULL; back. Ptr = NULL; } else front. Ptr = front. Ptr->next; temp. Ptr ->next = NULL; // defensive strategy delete temp. Ptr; } // end if } // end dequeue Function to remove front item from the queue

38 A Pointer-Based Implementation of the ADT Queue void Queue : : dequeue(Queue. Item. Type& queue. Front) { if (is. Empty()) cout << "empty queue, cannot dequeuen" ; else { // queue is not empty; retrieve and remove front queue. Front = front. Ptr ->item; dequeue(); // delete front cout << "Front element of the queue is “ << queue. Front << endl; } // end if } // end dequeue Function to retrieve and remove front item from the queue

39 A Pointer-Based Implementation of the ADT Queue void Queue : : get. Front(Queue. Item. Type& queue. Front) const { if (is. Empty()) cout << "empty queue, cannot get. Front" ; else { // queue is not empty; retrieve front queue. Front = front. Ptr ->item; cout << "Front element of the queue is " << queue. Front << endl; } } // end get. Front Function to retrieve front item of the queue

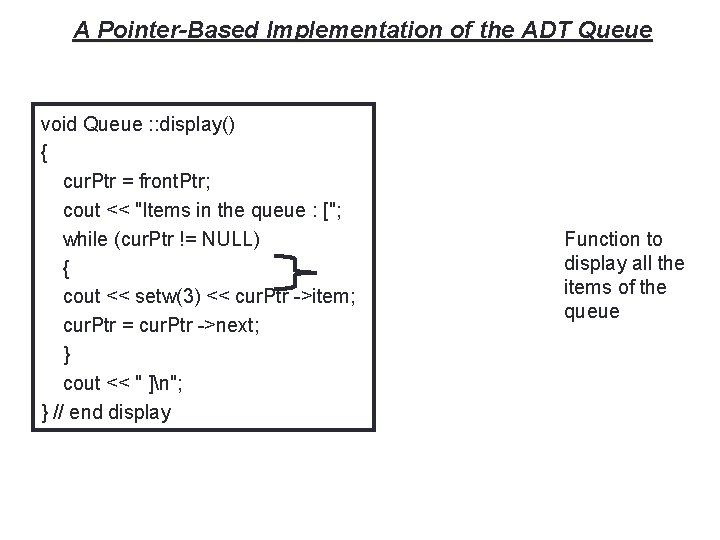
40 A Pointer-Based Implementation of the ADT Queue void Queue : : display() { cur. Ptr = front. Ptr; cout << "Items in the queue : ["; while (cur. Ptr != NULL) { cout << setw(3) << cur. Ptr ->item; cur. Ptr = cur. Ptr ->next; } cout << " ]n"; } // end display Function to display all the items of the queue

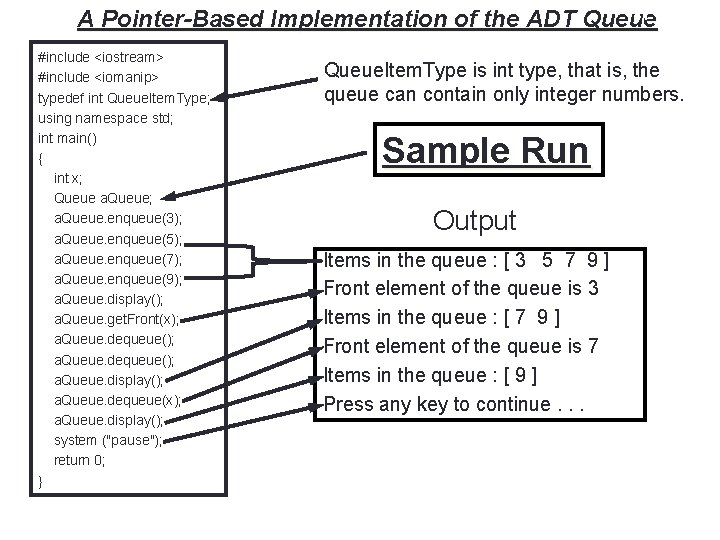
41 A Pointer-Based Implementation of the ADT Queue #include <iostream> #include <iomanip> typedef int Queue. Item. Type; using namespace std; int main() { int x; Queue a. Queue; a. Queue. enqueue(3); a. Queue. enqueue(5); a. Queue. enqueue(7); a. Queue. enqueue(9); a. Queue. display(); a. Queue. get. Front(x); a. Queue. dequeue(); a. Queue. display(); a. Queue. dequeue(x); a. Queue. display(); system ("pause"); return 0; } Queue. Item. Type is int type, that is, the queue can contain only integer numbers. Sample Run Output Items in the queue : [ 3 5 7 9 ] Front element of the queue is 3 Items in the queue : [ 7 9 ] Front element of the queue is 7 Items in the queue : [ 9 ] Press any key to continue. . .

42 The Standard Template Library Class queue

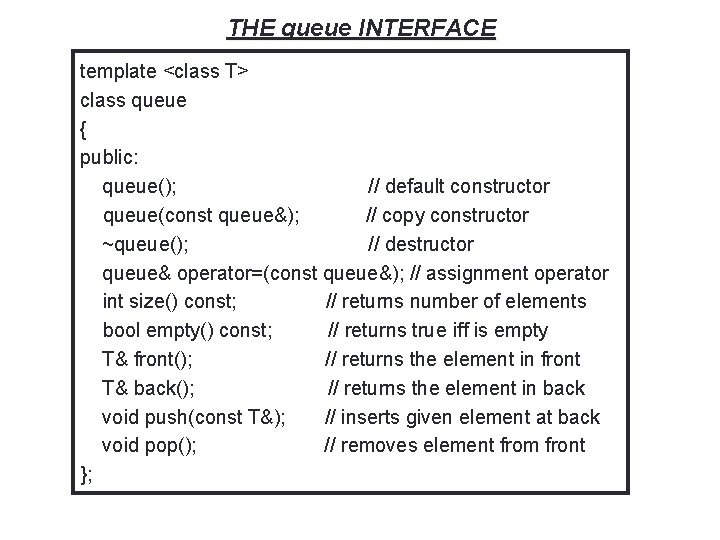
THE queue INTERFACE template <class T> class queue { public: queue(); // default constructor queue(const queue&); // copy constructor ~queue(); // destructor queue& operator=(const queue&); // assignment operator int size() const; // returns number of elements bool empty() const; // returns true iff is empty T& front(); // returns the element in front T& back(); // returns the element in back void push(const T&); // inserts given element at back void pop(); // removes element from front }; 43

Using a queue of Strings #include<iostream> #include<queue> using namespace std; int main() { queue<string> q; q. push ("Manoj"); q. push ("Sharaf"); q. push ("Wong"); q. push ("Azyyati"); q. push ("Norhana"); cout << "Size of queue is : " << q. size() << endl; cout << "n. Front element of the queue is "; cout << q. front(); cout << "n. Back element of the queue is "; cout << q. back(); cout << "nn. Elements in the queue : nn"; while (!q. empty()) { cout << q. front() << endl; q. pop(); } cout << endl; system("pause"); return 0; } 44 Sample Run Output Size of queue is : 5 Front element of the queue is Manoj Back element of the queue is Norhana Elements in the queue : Manoj Sharaf Wong Azyyati Norhana Press any key to continue. . .

45 Simple Applications Of The ADT Queue

46 Reading a String of Characters

47 When you enter characters at a keyboard, the system must retain them in the order in which you typed them. It could use a queue for this purpose, as the following pseudocode indicates: // read a string of characters from a // single line of input into a queue a. Queue. create. Queue() While (not end of line) { Read a new character ch a. Queue. enqueue(ch) } // end while

48 Once the characters are in a queue, the system can process them as necessary. For example: If you had typed an integer – without any mistakes, but possibly preceded or followed by blanks – the queue would contain digits and possibly blanks. If the digits are 2, 4, and 7, the system could convert them into the decimal value 247 by computing 10 * (10 * 2 + 4) + 7

49 The following pseudocode performs this conversion in general: // convert digits in a queue a. Queue into a // decimal integer n // get first digit, ignoring any leading blanks do { a. Queue. dequeue(ch) } while (ch is blank) // Assertion: ch contains first digit // compute n from digits in queue n=0 done = false do { n = 10 * n + integer that ch represents if (!a. Queue. is. Empty()) a. Queue. dequeue(ch) else done = true } while (!done and ch is a digit) // Assertion: n is result

50 Recognizing Palindromes

51 As you know that: a palindrome is a string of characters that reads the same from left to right as it does from right to left. As you have learned that you can use a stack to reverse the order of occurrences. You should realize by now that you can use a queue to preserve the order of occurrences. Thus, you can use both a queue and a stack to determine whether a string is a palindrome.

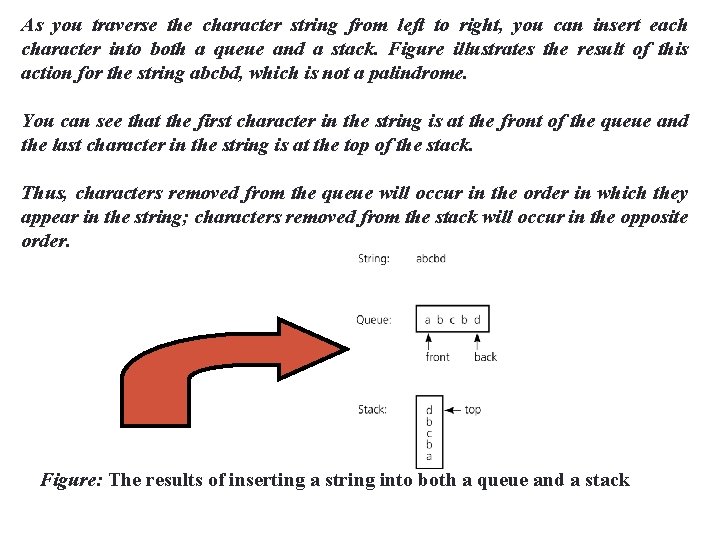
52 As you traverse the character string from left to right, you can insert each character into both a queue and a stack. Figure illustrates the result of this action for the string abcbd, which is not a palindrome. You can see that the first character in the string is at the front of the queue and the last character in the string is at the top of the stack. Thus, characters removed from the queue will occur in the order in which they appear in the string; characters removed from the stack will occur in the opposite order. Figure: The results of inserting a string into both a queue and a stack

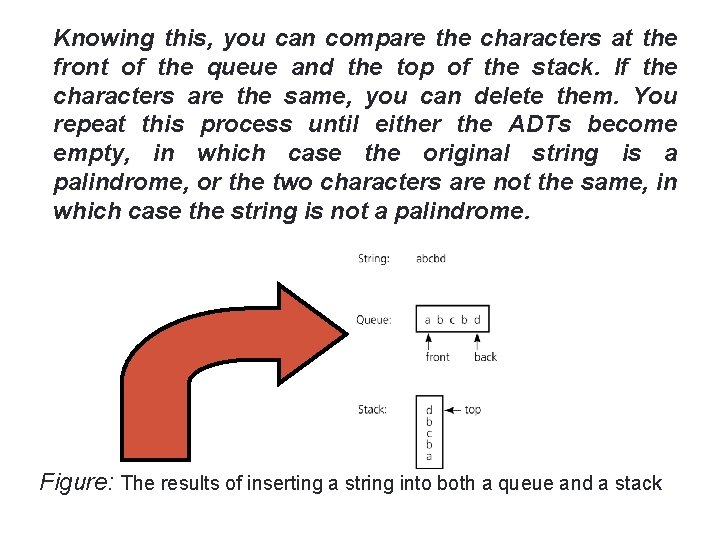
53 Knowing this, you can compare the characters at the front of the queue and the top of the stack. If the characters are the same, you can delete them. You repeat this process until either the ADTs become empty, in which case the original string is a palindrome, or the two characters are not the same, in which case the string is not a palindrome. Figure: The results of inserting a string into both a queue and a stack

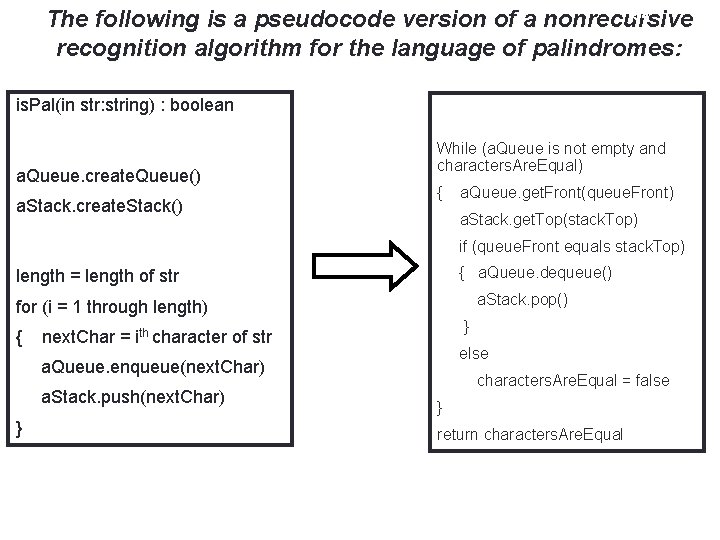
54 The following is a pseudocode version of a nonrecursive recognition algorithm for the language of palindromes: is. Pal(in str: string) : boolean // compare the queue characters // Determines whether str is a palindrome. // with the stack characters // create an empty queue and an empty stack While (a. Queue is not empty and characters. Are. Equal) a. Queue. create. Queue() a. Stack. create. Stack() // insert each character of the string into both { a. Queue. get. Front(queue. Front) a. Stack. get. Top(stack. Top) // the queue and the stack if (queue. Front equals stack. Top) length = length of str { a. Queue. dequeue() a. Stack. pop() for (i = 1 through length) { next. Char = ith character of str a. Queue. enqueue(next. Char) a. Stack. push(next. Char) } // end for } else characters. Are. Equal = false } // end while return characters. Are. Equal

55 PRIORITY QUEUES

PRIORITY QUEUES 56 The use of a queue structure ensures that the items are processed in the order they are received. For example, example in a banking environment, the customers who arrive first are served first. However, there are certain situations when this First In First Out rule needs to be relaxed somewhat. In a hospital environment, patients are, usually, seen in the order they arrive. Therefore, you could use a queue to ensure that the patients are seen in the order they arrive.

PRIORITY QUEUES 57 However, if a patient arrives with severe or life threatening symptoms, they are treated first. In other words, these patients take priority over the patients who can wait to be seen, such as those awaiting their routine annual check-up. For another example, in a shared environment, when print requests are sent to the printer, interactive programs take priority over batch processing programs

PRIORITY QUEUES 58 There are many other situations where some priority is assigned to the customers. To implement such a data structure in a program, we use special types of queues, called priority queues In a priority queue, customers or jobs with higher priority are pushed to the front of the queue. One way to implement a priority queue is to use an ordinary linked list, which keeps the items in order from the highest to lowest priority. However, an effective way to implement a priority queue is to use a treelike structure.

STL class priority_queue 59 Here is part of the interface for the Standard C++ priority_queue container class template: template <class T> class priority_queue { public: priority_queue(); priority_queue(const priority_queue&); ~priority_queue(); priority_queue& operator=(const priority_queue&); int size() const; // returns number of elements bool empty() const; // returns true iff this is empty const T& top() const; // returns the front element void push(const T&); // inserts given element at back void pop(); // removes element from front private: //. . }; These are the same functions as for the queue class template. The only significant difference is that the priority_queue class requires the template parameter T to be an ordinal type (i. e. , a type for which the comparison operators are defined) so that the pop() and top() functions remove and return the highest priority element instead of the first element.

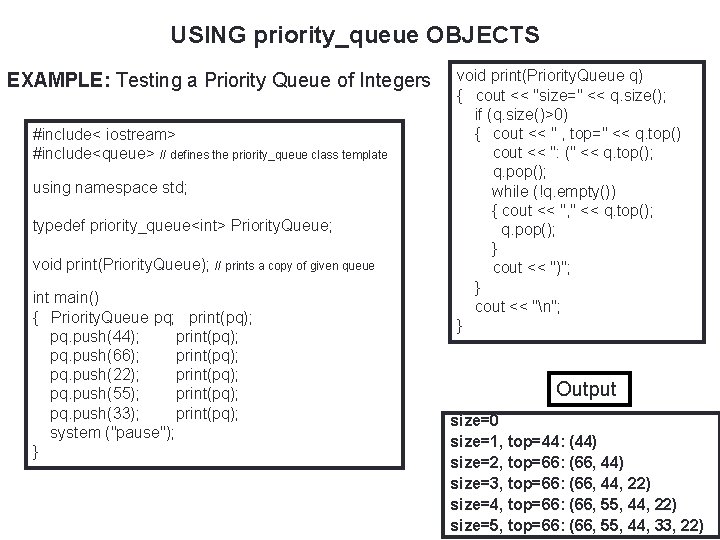
60 USING priority_queue OBJECTS EXAMPLE: Testing a Priority Queue of Integers #include< iostream> #include<queue> // defines the priority_queue class template using namespace std; typedef priority_queue<int> Priority. Queue; void print(Priority. Queue); // prints a copy of given queue int main() { Priority. Queue pq; print(pq); pq. push(44); print(pq); pq. push(66); print(pq); pq. push(22); print(pq); pq. push(55); print(pq); pq. push(33); print(pq); system ("pause"); } void print(Priority. Queue q) { cout << "size=" << q. size(); if (q. size()>0) { cout << " , top=" << q. top() cout << ": (" << q. top(); q. pop(); while (!q. empty()) { cout << ", " << q. top(); q. pop(); } cout << ")"; } cout << "n"; } Output size=0 size=1, top=44: (44) size=2, top=66: (66, 44) size=3, top=66: (66, 44, 22) size=4, top=66: (66, 55, 44, 22) size=5, top=66: (66, 55, 44, 33, 22)

PRIORITY QUEUES 61 The print() function suggests that the elements are stored in the priority queue in descending order But that is probably not true. The function uses the priority_queue : : pop() function to access the elements, and that member function is required to remove the elements in order of their priority. But there is no obligation on the priority_queue itself to store the elements in any particular order. Indeed, most implementations keep the elements only partially ordered.