1 QCD Quark Confinement Presented To American Physical

1 QCD Quark Confinement Presented To American Physical Society DPF 2006 + JSF 2006 31 October 2006 By Carl T. Case R&D Consulting

2 Outline • Framework for a Baryon Confinement Theory • Long Standing QCD Confinement Questions • Dirac Equation for Baryon Quarks (Composite of Q &G) • Solution of Dirac Equation for Composite Baryon Quark • Flavors & Generations • Baryon Mass Spectrum Calculations • Quark Generations

3 Framework and Approach for Theory • Massless Quarks Described by Dirac Equation • Massless Gluons Described by QCD Maxwell Equations • Seeking Eigenstates: Energy; Momenta; Angular Momenta; Parity • Using Hartree Self-Consistent-Field (SCF) Methodology – Converts Multi-Particle Problem to Multiple Single Particle Problems • Second Quantization – Enables Treating Quark & Gluon Operators on Common Basis • Gluon Fields Expressed as Complete Orthogonal Multipole Expansions – Lowest Order Multipoles Use for QCD Fields in Confinement Range – QCD Maxwell Eq. Commutator Terms contribute at Higher Orders

4 Long Standing Questions • Mechanism for Chiral Symmetry Breaking in QCD? • Confinement Mechanism For Quarks? • Confinement Mechanism For Gluons? • Why Do Quark Flavors Occur? • How Do Massless Quarks & Gluons Acquire Mass? • Is QCD a Calculable Theory in Confinement Range? • Are there Only Three Generations? … If so Why?

Quark-Gluon Velocity Synchronization Triggers Chiral Symmetry Breaking (CSB) • Consider Quarks & Gluons Moving with Same Velocity • Countervailing Magnetic Force Cancels Electric Force – Only a Color Magnetic Field Remains 5

6 Color Magnetic Bottle Confines Quarks • If Quarks and Gluons have same velocity, then CSB is triggered • Magnetic Bottle Pushes Quark into Force-Free Orbital Plane

7 CSB Simplifies the Dirac Equation • Before CSB • After CSB

8 Quantized Magnetic Flux Mechanism Confines Gluons • Quark’s Phase Angle is Given By Line Integral of Vector Potential or Surface Integral of Magnetic Field • Gluons Trapped by Circulating Quarks – Results in Quantized Bundles of Color Magnetic Flux Implies

9 Dirac Equation- Angular Momentum • From Chart 7 • Using Angular part of the operator • Dirac Equation can be written as

Dirac Equation. Composite Angular Momentum • Addition of Angular Momentum Quark & Gluon Operators Indicates that Total Orbital Ang. Mom. Is a Good Quantum Number where 10

Mass Acquisition by Quarks & Gluons • The Equatorial Plane is a Force-Free Region for Quarks • However, Well-Defined Angular Momentum for Quarks and Gluons • Implies Polar Angle, , is not Well-Defined; Location Uncertain • Tus, Magnetic Force Applies Inertial Drag Against Quarks & Gluons • Results in Kinetic Energy lost to Inertial Drag that shows up as Mass • Mass is Necessary for Quark-Gluon Composite to Conserve Energy 11

Dirac Equation - The Mass Term • Dirac Equation in terms of Quark-Gluon Composite Ang. Mom. where • Mass term can be added in Gauge Invariant manner 12

Flavor States & Amount of Mass Gain are Connected • CSB depends on Countervailing Magnetic Force cancelling Electric Force • Requires that the Countervailing Force is Constant • Quantized Flux Equations Produce a series of Topological Degenerate Ground States that Correspond 1 -to-1 to the Quark Flavor States • Winding Number, n, serves as Quantum Number Gluon • If Quark Mass is known, then Quark speed can be calculated. 13

14 Flavor State Data for Baryon Quarks

Is QCD a Calculable Theory in Confinement Range? • Key Issue – Calculation Strong Running Coupling Constant • Quantized Color Flux Equations Enable Calculation • Summary of Calculation is on Next Chart 15

Calculation of Strong Running Coupling Constant 16

Is QCD a Calculable Theory in Confinement Range? • Composite Q-G Dirac Equation provides Approximate Solutions 17

18 Approximate Energy Eigenstates for Baryon Quarks Baryon Mass is

Baryon Mass Spectra Calculations Results - Spin Only- 19

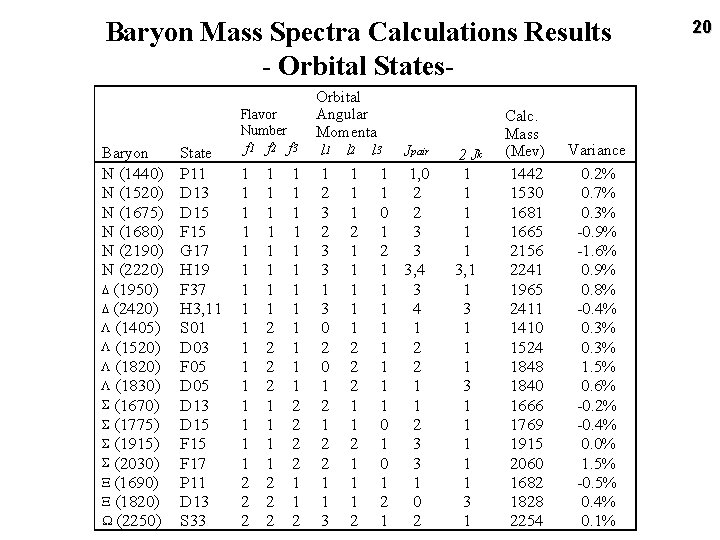
Baryon Mass Spectra Calculations Results - Orbital States. Baryon State f 1 f 2 f 3 Orbital Angular Momenta l 1 l 2 l 3 N (1440) N (1520) N (1675) N (1680) N (2190) N (2220) D (1950) D (2420) L (1405) L (1520) L (1830) S (1670) S (1775) S (1915) S (2030) X (1690) X (1820) W (2250) P 11 D 13 D 15 F 15 G 17 H 19 F 37 H 3, 11 S 01 D 03 F 05 D 13 D 15 F 17 P 11 D 13 S 33 1 1 1 1 2 2 2 1 2 3 3 1 3 0 2 0 1 2 2 1 1 3 Flavor Number 1 1 1 1 2 2 2 1 1 1 2 2 1 1 1 2 2 2 1 1 1 2 Jpair 1 1, 0 1 2 0 2 1 3 2 3 1 3, 4 1 3 1 4 1 1 1 2 1 1 0 2 1 3 0 3 1 1 2 0 1 2 2 Jk Calc. Mass (Mev) Variance 1 1 1 3, 1 1 3 1 1442 1530 1681 1665 2156 2241 1965 2411 1410 1524 1848 1840 1666 1769 1915 2060 1682 1828 2254 0. 2% 0. 7% 0. 3% -0. 9% -1. 6% 0. 9% 0. 8% -0. 4% 0. 3% 1. 5% 0. 6% -0. 2% -0. 4% 0. 0% 1. 5% -0. 5% 0. 4% 0. 1% 20

21 Empirical Scaling Law for Quark Speed C related to Coulomb Charge

Higher Flavor States? Are There more Than 3 Generations? • Scaling Law Suggests possible 4 th Gen. Quark (b’) w/ Mass > 100 Ge. V • Scaling Law also suggests all other quarks have energies are > Te. V which is well above the Quark-Gluon Plasma Critical Energy 22

Summary 23 • Dynamical Relationship Identified that Triggers CSB • Baryon Quarks Are Shown to be Composite of Massless Quarks and Gluons • Baryon Quarks Occupy a series of Degenerate Ground States Corresponding to the Six Quark Flavors – Each Flavor has Unique Quantum Number, Mass, and Speed • Baryon Mass Spectra Calculations are in Good Agreement with Experimental Data • Empirical Power Law for Speed of Quark Flavors indicates a Possible 4 th Generation Quark (b’) with Mass of 110 -160 Ge. V – Other Projected Quark Masses are above Quark-Gluon Plasma Limit

24 Backup Charts

Spin Percentage of Angular Momentum • Total Angular Momentum Distribution for Baryon is given by – Total = 3*(2 n+1+0. 5) = 3*(2 n+1. 5) • n=1 (u, d) Total = 3. 5 Spin %= 14. 3% • n=2 (s, c) Total = 5. 5 Spin %= 9. 1% • n=3 (b, t) Total = 7. 5 Spin %= 6. 7% 25

26 Theoretical Framework • Lowest Order Multipole Color Fields

Abstract Dirac equation is solved for 3 massless quarks under influence of generated color fields. If quarks and gluons have identical velocities, then chiral symmetry is broken. Color electric field is totally cancelled; quarks are trapped in color magnetic bottle; gluons are trapped by circulating quarks in quantized color magnetic flux bundles. Second quantization and Hartree approach are used to solve Dirac equation. Each quark along with its bundle of gluons behaves as a composite particle with mass gained from symmetry breaking. Solution exhibits a series of degenerate ground states that give rise to quark flavor states. Spinor wave function solutions from Dirac equation are used to calculate baryon mass spectrum. 27