1 Probability Class outline Probability definitions Random Error

1 Probability

Class outline Probability definitions Random Error Normal Distribution Probability Distributions and Decision Making 2

Probability What is the probability that I will obtain a head when flipping a nickel? What is the probability that a student in this class is female? Assume a couple has an equal probability of having a boy or a girl. Which is more likely to occur with 4 births? Bbbb Gggg bgbg 3

Probability What is the probability that I will obtain a head when flipping a nickel? 50% What is the probability that a student in this class is female? 4

Probability The chance of an event occurring/chance of all possible events occurring Ex. 1 Probability of heads on a coin flip = 1(heads)/2(heads or tails) Ex. 2 Probability of rolling a two on a die 1/6 5

Probability Independent Mutually exclusive Not influenced by probability of another event Cannot occur at the same time Conditional Dependent upon another event 6

Probability Rules: Mutually Exclusive Events Probability of A OR B (heads or tails) Probability of A + Probability of B . 5 +. 5 = 1 or 1 -0 = 1 Multiple Events (e. g. Flip a coin twice) Probability of A AND B (Head on first flip, tails on second) Probability of A * Probability of B . 5*. 5 =. 25 Heads first flip, heads OR tails on second) Probability of A * (Probability of A or B) . 5*1 = . 5 7

Probability Rules: Mutually Exclusive Events Probability of three heads in a row . 5*. 5=. 125 Probability of two heads in a row and a head or tail . 5*(1)=. 25 8

Practice What is the probability of obtaining five (5) heads in a row? What is the probability of obtaining a head after obtaining four heads in a row? 9

Practice During World War Two I Japanese Ace pilot Saburo Sakai in Samurai recalled his experiences on an airbase in New Guniea: “The enemy did his best to make sure we did not sleep at night. They almost unfailingly attacked our air base, dropping bombs in the darkness. It got so bad that we often abandoned our sleeping quarters and went out to the runway after dark to sleep in the craters dug by enemy bombs. Our theory was that there little probability of an enemy bomb striking exactly where one had fallen previously. ” 1010 1. What assumption did Saburo Sakai and his colleagues make about the relationship about where bombs fall? 2. Assume that bombing during World War Two was relatively inaccurate and within a five mile radius essentially random. If Saburo and his colleagues wanted the best chance for a good night’s sleep, where should they sleep, in their beds or in craters? 10

Random Error Estimate my height Write on a piece of paper Guess what the temperature is outside now (don’t cheat!) 11

Random Error There is a certain amount of error associated with your estimates Typically the errors will fall symmetrically around the true estimate Normal distribution, a type of probability distribution Without knowing my true height your best guess would be the mean You would be less confident the further away from the mean a guess is 12

Probability Distribution The frequency of events with a random component have a distribution Normal Height IQ T Chi-square 13

Probability Distribution Normal Distribution In large samples random numbers (e. g. coin flip, roll of die, prediction errors) will be distributed normally Central limit theorem Law of large numbers 14

Central limit theorem When numerous random samples are drawn from a population distribution, the shape of the distribution will resemble a normal distribution if enough samples are drawn (law of large numbers) 15

Probability Distributions and Decision Making An example with a coin One of the coins in my hand is “fake” or has two heads How many heads do I have to obtain before you are willing to bet the coin is fake? 16

Probability Distributions and Decision Making An example with a coin One of the coins in my hand is “fake” or has two heads How many heads do I have to obtain before you are willing to bet the coin is fake? Probability of one flip without a heads 50% Probability of two flips without a heads 25% Probability of three flips without a heads 12. 5% Probability of four flips without a heads 6. 25% 17

Probability Distributions and Decision Making An example with a die One of the dies in my hand does not have a one How many rolls do you have to observe before determining if the die is fake? 18

Probability Distributions and Decision Making An example with a die One of the dies in my hand does not have a one How many rolls do you have to observe before determining if the die is fake? Probability of one roll without a one 83. 33% Probability of two rolls without a one 69. 4% . . . Probability of ten rolls without a one 16. 2% . 19

Probability Distributions and Decision Making If we know the probability distribution (e. g. how likely to get x number of heads or x number of rolls without a one) we can make informed decisions 20

Probability Distributions and Decision Making The link to Social Science and Planning If we know the properties of a given probability distribution we can estimate the probability of an event occurring Ex. Normal distribution The probability of x depends on the mean and the standard deviation Z-score tells us how many standard deviations x is from the mean We can use the z-score to determine the probability of x 21

Z STATISTIC 22

Example in class problems Vince Yosarian works for the Bureau of Forms. His manager has reprimanded Vince because she feels that he has not performed up to standard for processing forms at the bureau, the crucial part of the job. At the bureau, the number of forms processed by employees is normally distributed, with a mean of 67 forms per employee per day, with a standard deviation of 7. His manager has calculated that Vince’s average rate is 50 forms processed per day. What percentage of employees at the bureau process fewer forms than Vince? What percentage of employees at the bureau process more forms than Vince? Does the manager’s complaint seem justified or not? 23

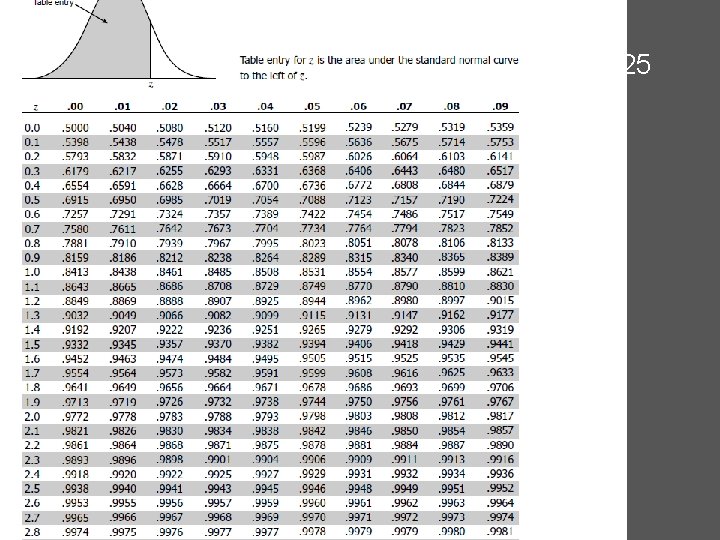
Example in class problems 1. Calculate z-statistic z = (50 -67) /7 = -2. 43 24
25

Example in class problems 1. z = (50 -67) /7 = -2. 43 Associated probability =. 4925 Interpretation: 99. 25% of workers are faster 26

Example Parnelli Jones, a vehicle manager for the northeast region of the forestry service, is charged with purchasing automobiles for service use. Because forestry service employees often have to drive long distances in isolated regions, Parnelli is very concerned about gasoline mileage for the vehicle fleet. One automobile manufac-turer has told him that the particular model of vehicle that interests him has averaged 27. 3 miles per gallon in road tests with a standard deviation of 3. 1 (normal distribution). Parnelli would like to be able to tell his superiors at the forestry service that the cars will get at least 25 miles to the gallon. According to the road test data, what percentage of the cars can be expected to meet this criterion? Parnelli also thinks that his superiors might settle for cars that got 24 miles to the gallon or better. What percentage of the cars can be expected to meet this criterion? 27

Example in class problems 2. a. z = (25 -27. 3) /3. 1 = -. 7 Associated probability =. 24196 Interpretation: 24. 2% of cars will not meet criterion Please note that the z-table in the textbook gives the percentage between the mean and. 7 standard deviations below the mean. 24. 2% represents the number that falls below that value b. z = (24 -27. 3) /3. 1 = -1. 1 Associated probability. 13567 Interpretation: 13. 6% of cars will not meet criterion Please note that the z-table in the textbook gives the percentage between the mean and. 7 standard deviations below the mean. 13. 6% represents the number that falls below that value 28

T-distribution 29
- Slides: 29