1 PCP Proof Map Sum Check GapQSOn 2

1

PCP Proof Map Sum Check Gap-QS[O(n), , 2| |-1] quadratic equations of constant size with consistency assumptions Gap-QScons[O(1), , 2| |-1] Consistent Reader Gap-QS*[O(1), , | |- ] Error correcting codes conjunctions of constant number of quadratic equations, whose dependencies are constant. Gap-QS[O(1), , 2| |-1] 2

Using consistent readers 3

Consistent Readers Remove Consistency Assumptions: Concept: Readers are plugged into equations, and ensure (w. h. p) the domain variables are only assigned values corresponding to some permissible polynomial. Def: A function f is called a -permissible polynomial (with respect to an assignment A) if at least 1 - of the points x are assigned the value of a dimension d and degree r polynomial. 4

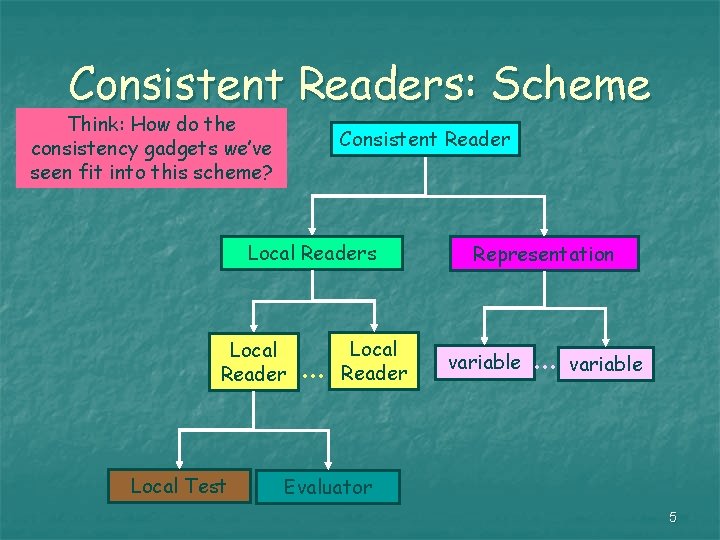
Consistent Readers: Scheme Think: How do the consistency gadgets we’ve seen fit into this scheme? Consistent Reader Local Readers Local Reader Local Test . . . Local Reader Representation variable . . . variable Evaluator 5

The Desired Properties of A Consistent Reader n n Efficiency: There is only a polynomial number of local readers. Low Dependency: Each local reader depends on a constant number of representation variables. Linearity: Each local test is a conjunction of linear equations over representation variables. Each evaluator is a linear combination of such. Range: All variables should range over . 6

The Desired Properties of A Consistent Reader n n Completeness: All local tests accept every assignment to the variables corresponding to some -permissible polynomial. Moreover, every evaluator must return the evaluations of that polynomial. Soundness: At most an fraction of the tests can be satisfied when no -permissible polynomial exists. 7

The Consistent Reader We Have Representation: n One variable for every cube (affine subspace) of dimension k+2, containing the k points corresponding to variables from this domain appearing in equations. (Values of the variables range over all degree-r, dimension k+2 polynomials) n One variable for every point x d. (Values of the variables range over ). 8

The Consistent Reader We Have Consistent-Reader: n One local-reader for every cube-variable C and a point-variable y C, which n n rejects if A’s value for C restricted to y disagrees with A’s value on y, otherwise: returns A’s values on C restricted to x 1, . . . , xk. 9

Does This Consistent Reader Suffice? n n n Implicitly, our consistent reader relies itself on consistency assumptions. This will be resolved in the proof of the Composition-Recursion lemma, assuring us there exists a satisfactory consistent reader. In the meantime, let us assume that, and continue with the PCP proof. You’d might want to take a better look at the desired properties and the construction first. 10

Gap-QScons Reduces To Gap. Note the uniformity of the construction: QS* Each equation contributes the exact same The Construction: number of conjunctions. n Let p be one of the equations. n Assume there are k domains F 1, . . . , Fk (associated with k consistent readers). n Generate a conjunction for every choice of one local reader of each consistent reader. n Each conjunction has the following format: the original equation, where each domain variable is replaced by its evaluation local test 1 . . . local test k 11

Correctness: Completeness n n n Let A denote an instance of Gap-QScons[O(1), , 2/| |]. Let B denote the corresponding instance of Gap-QS*[O(1), , | |- ]. Completeness: a good satisfying assignment for A can be easily extended into a satisfying assignment for B. 12

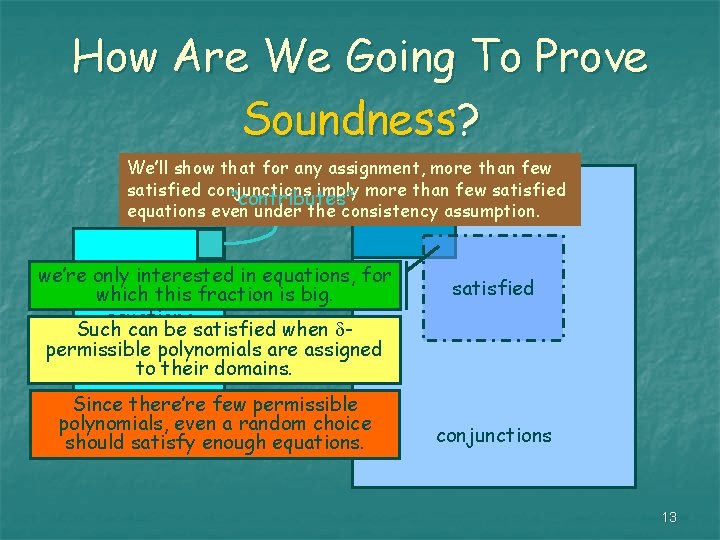
How Are We Going To Prove Soundness? We’ll show that for any assignment, more than few satisfied conjunctions imply more than few satisfied “contributes” equations even under the consistency assumption. we’re only interested in equations, for which this fraction is big. equations Such can be satisfied when permissible polynomials are assigned to their domains. Since there’re few permissible polynomials, even a random choice should satisfy enough equations. satisfied conjunctions 13

Correctness: Soundness n n n Suppose there exists an assignment which satisfies >| |- of B’s conjunctions. Let p be an equation which more than k of its conjunctions are satisfiable. At least -k of the equations satisfy this. 14

Correctness: Soundness n n For every reader, at most of the local tests err. Overall at most k of all local tests err. Hence there exists a satisfied conjunction with no erroneous tests. satisfying assignment for p which assigns every domain a -permissible polynomial. 15

Auxiliary Lemma: Not Many Permissible Polynomials Lemma: For any big enough ( 2>4 rd| |-1), there are less than 2 -1 -permissible polynomials. Proof: n Suppose there were 2 -1 -permissible polynomials. n Each agrees with every other polynomial on at most rd| |-1 of the points. 16

Auxiliary Lemma: Not Many Permissible Polynomials n n n Overall on at most a 2 -1 rd| |-1 fraction there exists some polynomial it agrees with. Which is less than ½ by the choice of . But a -permissible polynomial agrees with the assignment on at least of the points. 17

Auxiliary Lemma: Not Many Permissible Polynomials n n Thus, for each polynomial for more than ½ of the points it’s the only one agreeing with the assignment on them. Contradiction! Recall that by our assumption there as many as 2 -1 polynomials. � 18

Proof of Soundness Continued n n If we assign each domain a random permissible polynomial, p should be satisfied with probability at least O( k). Hence the expected number of satisfied equations is at least O(( -k ) k). Thus at least one assignment satisfies that many equations. For an appropriate choice of the parameter , this number is greater than 2/| |. � 19

PCP Proof Map Sum Check Gap-QS[O(n), , 2| |-1] quadratic equations of constant size with consistency assumptions Gap-QScons[O(1), , 2| |-1] Consistent Reader BUT it remains to prove the compositionrecursion lemma. . . Gap-QS*[O(1), , | |- ] Error correcting codes conjunctions of constant number of quadratic equations, whose dependencies are constant. Gap-QS[O(1), , 2| |-1] 20