1 PCP Proof Map Sum Check GapQSOn 2

1

PCP Proof Map Sum Check Gap-QS[O(n), , 2| |-1] quadratic equations of constant size with consistency assumptions Gap-QScons[O(1), , 2| |-1] Consistent Reader BUT it remains to prove the compositionrecursion lemma. . . Gap-QS*[O(1), , | |- ] Error correcting codes conjunctions of constant number of quadratic equations, whose dependencies are constant. Gap-QS[O(1), , 2| |-1] 2

Using error correcting codes 3

Conjunctions of Equations Definition (Gap-QS*[D 1, D 2, , ]): Instance: a set of n conjunctions of D 1 quadratic equations (polynomials) over . Each equation depends on at most D 2 variables. Problem: to distinguish between: There is an assignment satisfying all the conjunctions. No more than an fraction of the conjunctions can be satisfied simultaneously. 4

Conjunctions of Equations An example instance of Gap-QS*[2, 1, Z 2, ½]: Notice that we can satisfy more than a half of the equations!! Henceforth, we’ll assume the number of equations in all the conjunctions is the same. Is this a restriction? 5

The reduction Claim: Gap-QS*[D 1, D 2, , ] reduces to Gap. QS[D 1·D 2, , +| |-1] (as long as | |D 1 is at most polynomial). Proof: Given an instance of Gap-QS*[D 1, D 2, , ], replace each conjunction with all linear combinations of its polynomials. (i. e. apply Hadamard code to conjuncts) 6

Correctness of the Reduction n n If the original system had a common solution, so does the new system. Otherwise, fix an assignment to the variables of the system and observe the two instances: 7

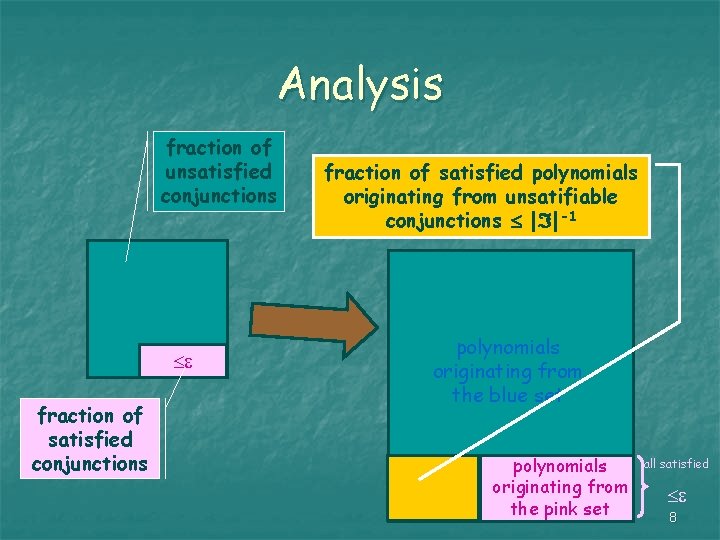
Analysis fraction of unsatisfied conjunctions fraction of satisfied polynomials originating from unsatifiable conjunctions | |-1 polynomials originating from the blue set polynomials originating from the pink set all satisfied 8

Relaxation n n Yes instance of Gap-QS*[D 1, D 2, , ] are transformed into Yes instances of Gap. QS[D 1·D 2, , +| |-1]. No instance of Gap-QS*[D 1, D 2, , ] are transformed into No instances of Gap. QS[D 1·D 2, , +| |-1]. The construction is efficient when | |D 1 is at most polynomial in the size of the input. What proves the claim. � 9

Amplification Claim: For any constant C, Gap-QS[D, , ] reduces to Gap-QS[C·D, , C+| |-1] (When | | is at most polynomial in the size of the input). Proof: Given an instance of Gap-QS[D, , ], generate the set of all linear combinations of C polynomials. By an argument similar to the former, the claim holds. � 10

PCP Proof Map Sum Check Gap-QS[O(n), , 2| |-1] quadratic equations of constant size with consistency assumptions Gap-QScons[O(1), , 2| |-1] Consistent Reader BUT it remains to prove the compositionrecursion lemma. . . Gap-QS*[O(1), , | |- ] Error correcting codes conjunctions of constant number of quadratic equations, whose dependencies are constant. Gap-QS[O(1), , 2| |-1] 11