1 Overview of Automata Theory and Proof Methods

1. Overview of Automata Theory and Proof Methods Automata theory studies abstract computing devices, or machines Ø Turing machines were proposed by A. Turing in the 1930 s as an abstraction for general-purpose computing machines Ø Finite automata, which are simpler (less powerful) machines, were proposed in the 1940 s and 1950 s to model brain functions Ø Formal languages, which are closely related the pushdown automata machines, were proposed by linguist N. Chomsky in the 1950 s Ø The study of time and space efficiency of programs led to models for tractable and intractable problems, e. g. NPcomplete and NP-hard problems

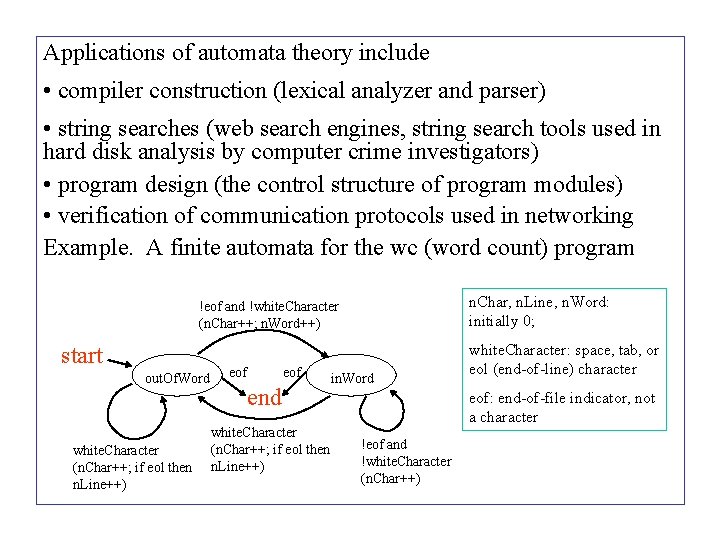
Applications of automata theory include • compiler construction (lexical analyzer and parser) • string searches (web search engines, string search tools used in hard disk analysis by computer crime investigators) • program design (the control structure of program modules) • verification of communication protocols used in networking Example. A finite automata for the wc (word count) program n. Char, n. Line, n. Word: initially 0; !eof and !white. Character (n. Char++; n. Word++) start out. Of. Word white. Character (n. Char++; if eol then n. Line++) eof end white. Character (n. Char++; if eol then n. Line++) in. Word white. Character: space, tab, or eol (end-of-line) character eof: end-of-file indicator, not a character !eof and !white. Character (n. Char++)

Formal Proof Methods: • Statements in the if-then form: Ø if x 4 and x is an integer then 2 x x 2. Ø if A B and B C then A C. • Use definitions and theorems: Ø Let S U, where S is finite and U is infinite. Prove U – S is infinite. (Definition: A set A is finite if |A| = n, a natural number (more precisely, if there is a bijection between A and the set {1, 2, …, n}). A set is infinite is it is not finite. Theorem: Let A B = U and A B = . If both A and B are finite, then |A| + |B| = |U|. ) • Statements in the iff (if-and-only-if) form: Ø Let x be a real number. Then x is an integer iff x = x.

Formal Proof Methods (cont’d): • Statements without assumptions: Ø sin 2 + cos 2 = 1. Ø R (S T) = (R S) (R T). (There is a typographical error on the right-hand side of this identity on p. 14 of the text, in two places. ) • Proof by contradiction: Ø (The pigeonhole principle) If n+1 pigeons nest in n holes, then there exists one hole that has at least two pigeons. • Counterexamples: Ø (Conjecture) The expression n 2 – n + 41 is a prime for all natural number n. (A counterexample. Try n = 41. The value is 412 – 41 + 41 = 412, not a prime. )

Formal Proof Methods (cont’d): • Use of universal (for all, ) and existential (there exists, ) quantifiers: Ø (Definition) A set S is infinite if n N A S such that |A| = n; that is, for all natural number n the set S contains a subset A whose size equals n. Ø Given two positive functions f(n) and g(n) that are defined on natural numbers n. We say f(n) = O(g(n)), or f = O(g) in short, if constants c and k such that n k, f(n) c g(n); that is, f(n) c g(n) for all n that is larger than some threshold value k, where c and k are some constants (independent of n). Ø (De. Morgan’s Laws) ( n P(n)) n ( P(n)); ( n P(n)) n ( P(n)). For example, the negation of all apples in the bag are red is there exists a non-red apple in the bag; the negation of there exists a rainy day last month is every day of last month is non-rainy.

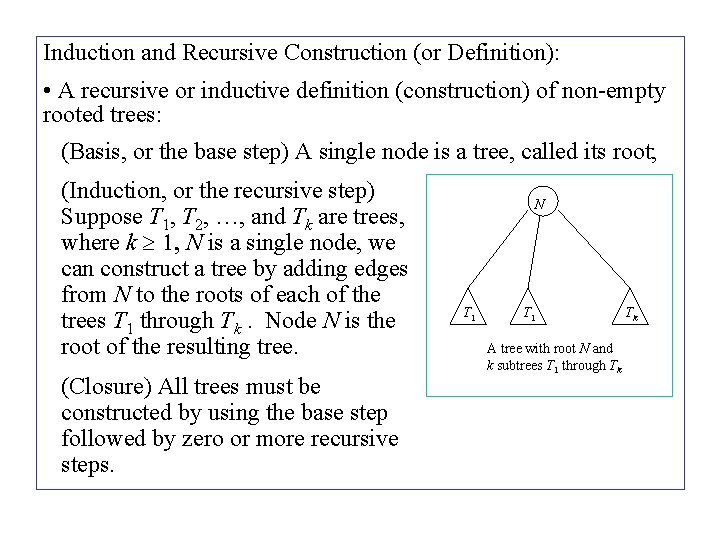
Induction and Recursive Construction (or Definition): • A recursive or inductive definition (construction) of non-empty rooted trees: (Basis, or the base step) A single node is a tree, called its root; (Induction, or the recursive step) Suppose T 1, T 2, …, and Tk are trees, where k 1, N is a single node, we can construct a tree by adding edges from N to the roots of each of the trees T 1 through Tk. Node N is the root of the resulting tree. (Closure) All trees must be constructed by using the base step followed by zero or more recursive steps. N T 1 A tree with root N and k subtrees T 1 through Tk Tk

Induction and Recursive Construction (cont’d): • Every (rooted) tree has one more node than it has edges. (Proof) We use induction on the number of recursive steps used in constructing a tree. We use the notations n and e for the numbers of nodes and edges, respectively. (Basis) Suppose a tree is constructed by the base step only. In this case, the tree has one single node and no edges; thus, n = 1 and e = 0, so n = e + 1. (Induction) We assume every tree satisfies the node-edge relation if it is constructed using m steps. We now consider a tree T which uses m+1 steps. The last step must be connecting k subtrees T 1 through Tk to a root N. Since each subtree uses m steps (because the whole tree uses m+1 steps, one of which is the last step), each subtree Ti satisfies the relations ni = ei + 1, where ni and ei denote tree Ti’s numbers of nodes and edges, resp. Thus, 1 i n ni = 1 i n (ei + 1). Since tree T has (1+ 1 i n ni) nodes and has 1 i n (ei + 1) edges, so the node-edge relation is satisfied by tree T.

Strings and Languages: • (Definitions and notations) An alphabet is a finite, non-empty set of symbols. A string (or a word) is a finite sequence of symbols from some alphabet. The number of symbols in a string w is the length of the string, denoted |w|. Thus, if the alphabet = {0, 1}, a string w = 011 has a length |011| = 3. Two strings u and v can be concatenated, denoted uv, by writing out the symbols of u followed by those of v. Thus, |uv| = |u| + |v|. Note that uv vu in general. The empty string (a string of no symbols) is denoted (sometimes ). Note that |w| = 0 iff w =. • (Definition related to languages) Let be an alphabet. Then 1 = , 2 = the set of strings of length 2 over , similarly for 3, 4, etc. By convention, 0 = { }. The set of all (finite) strings over is denoted * = 0 1 2 …, which is an infinite union. Any subset L * is called a language over . In particular, the empty set is a language. Note that { }.

Some Sample languages: • Define L = {0 n 1 n | n 0} = { , 01, 0011, 000111, …} = the set of strings that start with any number of 0’s followed by the same number of 1’s, including the empty string . • (A recursive or inductive definition of a language S) (Base step) The empty string belongs to S. (Recursive step) If a string w belongs to S, then the string 0 w 1 also belongs to S. (Closure) No other strings belong to S unless they are constructed by applying zero or more recursive steps after the base step. To prove L = S, we prove two parts: (1) S L and (2) L S. Proving (1) means proving x S implies x L, which can be done by induction on the steps used in constructing string x. To prove (2), use induction on n to prove 0 n 1 n S for all n 0.

Some Laws Related to Strings and Languages: Let A, B, and C denote sets of strings over an alphabet . • (Definition) The concatenation set AB = {uv | u A and v B}; that is, AB contains all possible concatenations of any string of A followed by any string of B. The Kleene star A* = A 0 A 1 A 2 …, where A 0 = { }; thus, A* contains all strings formed by concatenating an arbitrary number of strings of A including multiple occurrences of the same string in the concatenation. • The following are commonly used theorems: Ø if A B then AC BC and A* B*; Ø A(B C) = AB AC ; (B C)A = BA CA; Ø A(B C) AB AC; however, the two sides are in general not equal, e. g. , when A = {a, ab}, B = {b}, C = {bb}, A(B C) = A = , but AB AC = {ab, abb} {abb, abbb} = {abb}.