1 OUTLINE Pendugaan Titik Parameter Konsep Dasar Persamaan



















- Slides: 34

1

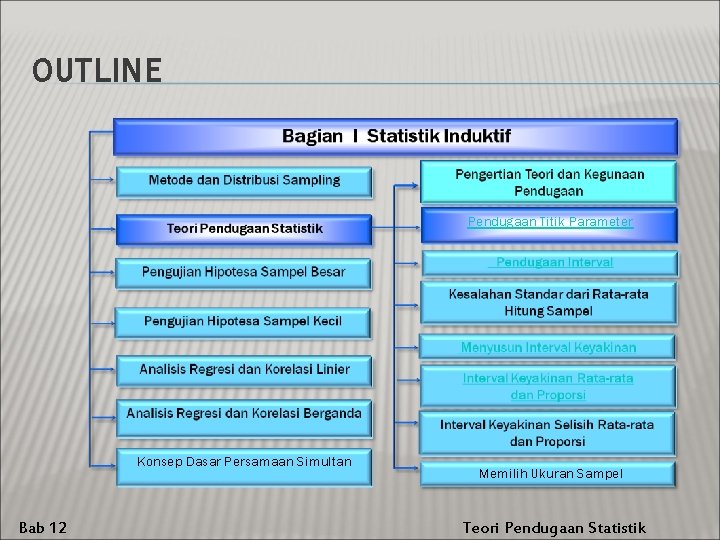
OUTLINE Pendugaan Titik Parameter Konsep Dasar Persamaan Simultan Bab 12 Memilih Ukuran Sampel Teori Pendugaan Statistik

INFERENSI STATISTIK Inferensi statistik mencakup semua metode yang digunakan dalam penarikan kesimpulan atau generalisasi mengenai populasi. Inferensi Statistik Pendugaan Parameter Pengujian Hipotesis 3

PENDUGAAN PARAMETER Pendugaan parameter berarti melakukan estimasi terhadap nilai dugaan/taksiran suatu parameter tertentu, karena pada umumnya nilai parameter suatu distribusi tidak diketahui Contoh : Seorang calon dalam suatu pemilihan ingin menduga proporsi yang sebenarnya pemilih yang akan memilihnya, dengan cara mengambil 100 orang secara acak untuk ditanyai pendapatnya. Proporsi pemilih yang menyukai calon tersebut dapat digunakan sebagai dugaan bagi proporsi populasi yang sebenarnya. 4

Metode Pendugaan Parameter Metode Pendugaan Klasik Metode Pendugaan Bayes Metode Pendugaan Klasik : Pendugaan dilakukan berdasarkan sepenuhnya pada informasi sampel yang diambil dari populasi. Metode Pendugaan Bayes : Pendugaan dengan menggabungkan informasi yang terkandung dalam sampel dengan informasi lain yang telah tersedia sebelumnya yaitu pengetahuan subyektif mengenai distribusi probabilitas parameter. 5

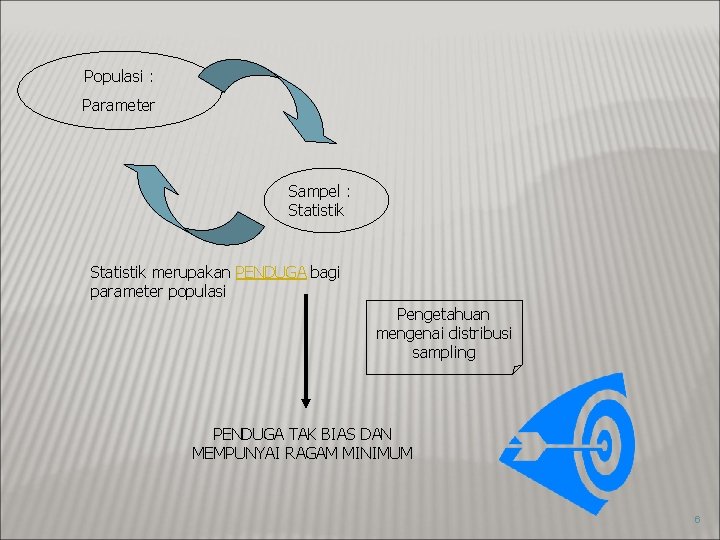
Populasi : Parameter Sampel : Statistik merupakan PENDUGA bagi parameter populasi Pengetahuan mengenai distribusi sampling PENDUGA TAK BIAS DAN MEMPUNYAI RAGAM MINIMUM 6

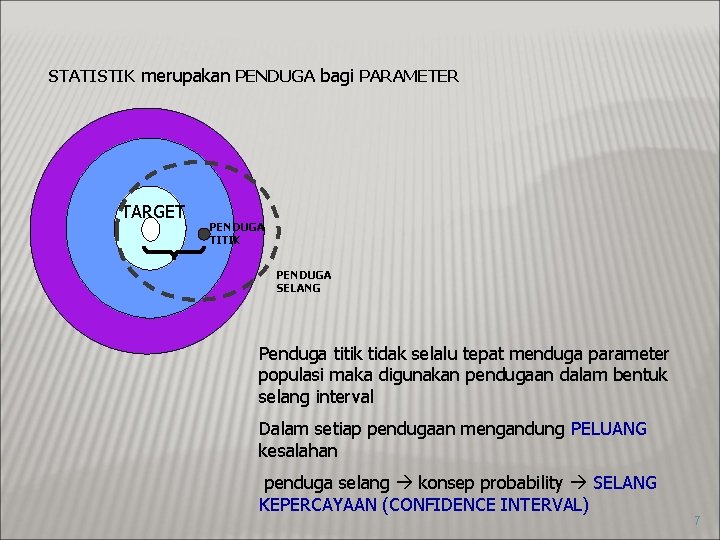
STATISTIK merupakan PENDUGA bagi PARAMETER TARGET PENDUGA TITIK PENDUGA SELANG Penduga titik tidak selalu tepat menduga parameter populasi maka digunakan pendugaan dalam bentuk selang interval Dalam setiap pendugaan mengandung PELUANG kesalahan penduga selang konsep probability SELANG KEPERCAYAAN (CONFIDENCE INTERVAL) 7

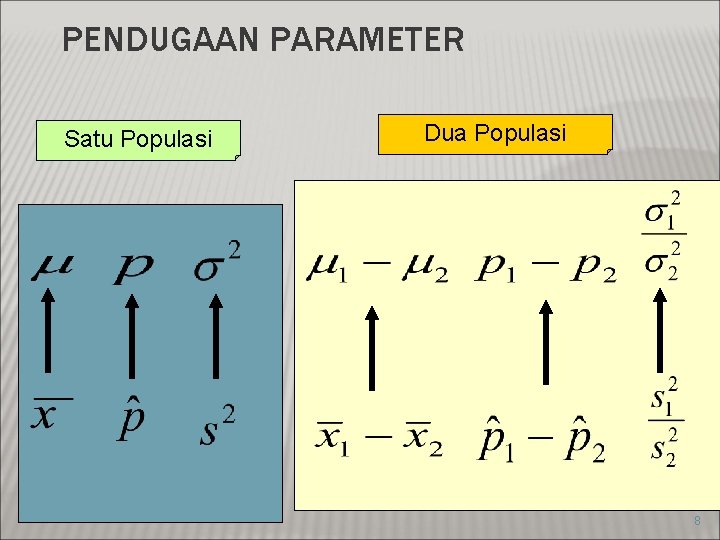
PENDUGAAN PARAMETER Satu Populasi Dua Populasi 8

PENDUGA TUNGGAL SEBAGAI FUNGSI UNSUR POPULASI atau S = f( X 1, X 2, …, X n) di mana: X X X s 2 = 1 (Xi - X ) 2 n-1 2 s = 1 {(X 1 - X ) 2 + (X 2 - Xx) 2 + … + (Xn - X ) 2} = 1 Xi n = 1 (X 1 + X 2 + … + X n) n n-1 f( X 2) f(X 1) f( X 3) X Bab 12: Teori Pendugaan Statistik Pendugaan Titik Paraneter

SIFAT-SIFAT PENDUGA Penduga Tidak Bias • Unbiased estimator Bab 12: Teori Pendugaan Statistik Penduga Efisien • Efficient estimator Penduga Konsisten • Consistent estimator Pendugaan Titik Paraneter 10

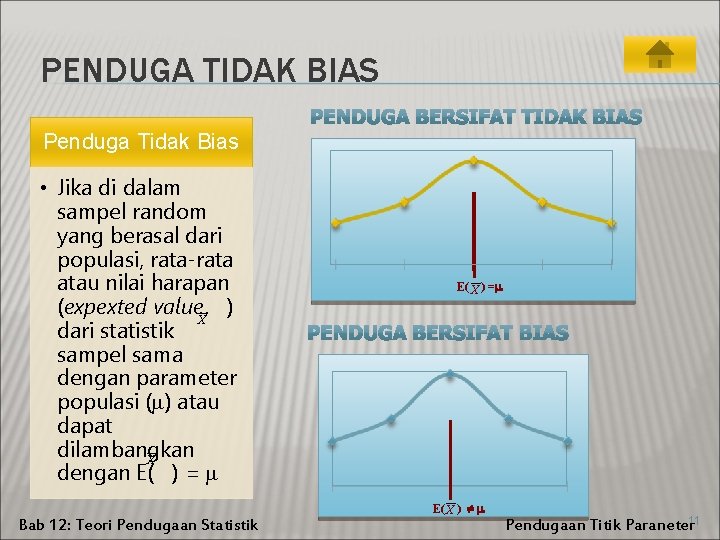
PENDUGA TIDAK BIAS Penduga Tidak Bias • Jika di dalam sampel random yang berasal dari populasi, rata-rata atau nilai harapan (expexted value, X ) dari statistik sampel sama dengan parameter populasi ( ) atau dapat dilambangkan X dengan E( ) = Bab 12: Teori Pendugaan Statistik E( X ) = E( X ) Pendugaan Titik Paraneter 11

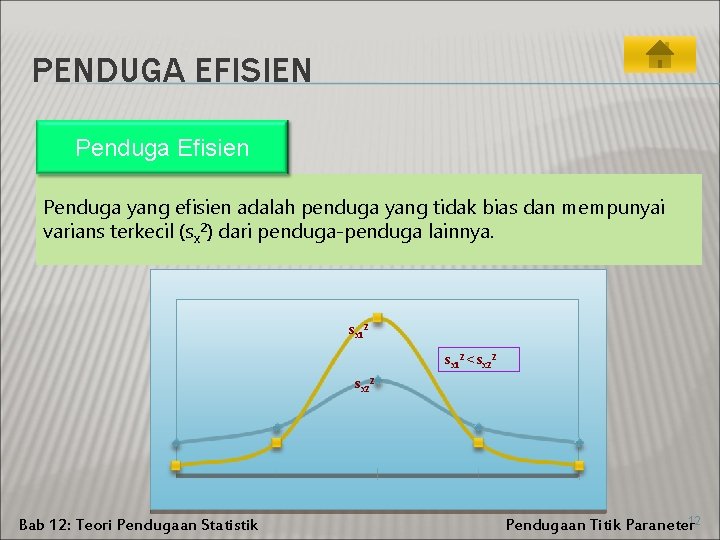
PENDUGA EFISIEN Penduga Efisien Penduga yang efisien adalah penduga yang tidak bias dan mempunyai varians terkecil (sx 2) dari penduga-penduga lainnya. sx 12 < sx 22 Bab 12: Teori Pendugaan Statistik Pendugaan Titik Paraneter 12

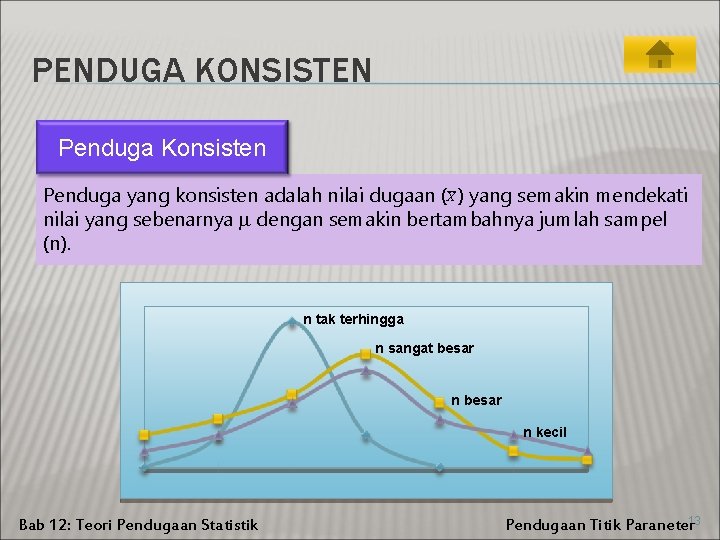
PENDUGA KONSISTEN Penduga Konsisten Penduga yang konsisten adalah nilai dugaan (X ) yang semakin mendekati nilai yang sebenarnya dengan semakin bertambahnya jumlah sampel (n). n tak terhingga n sangat besar n kecil Bab 12: Teori Pendugaan Statistik Pendugaan Titik Paraneter 13

PENDUGAAN INTERVAL Pendugaan interval menyatakan jarak di dalam mana suatu parameter populasi mungkin berada. Bab 12: Teori Pendugaan Statistik Pendugaan Interval

RUMUS INTERVAL PENDUGAAN (s – Zsx < P < s + Zsx ) = C S : statistik yang merupakan penduga parameter populasi (P) P : parameter populasi yang tidak diketahui Sx : standar deviasi distribusi sampel statistik Z : suatu nilai yang ditentukan oleh probabilitas yang berhubungan dengan pendugaan interval, Nilai Z diperoleh dari tabel luas di bawah kurva normal C : Probabilitas atau tingkat keyakinan yang dalam praktek sudah ditentukan dahulu s – Zsx : nilai batas bawah keyakinan s + Zsx : nilai batas keyakinan Bab 12: Teori Pendugaan Statistik Pendugaan Interval 15

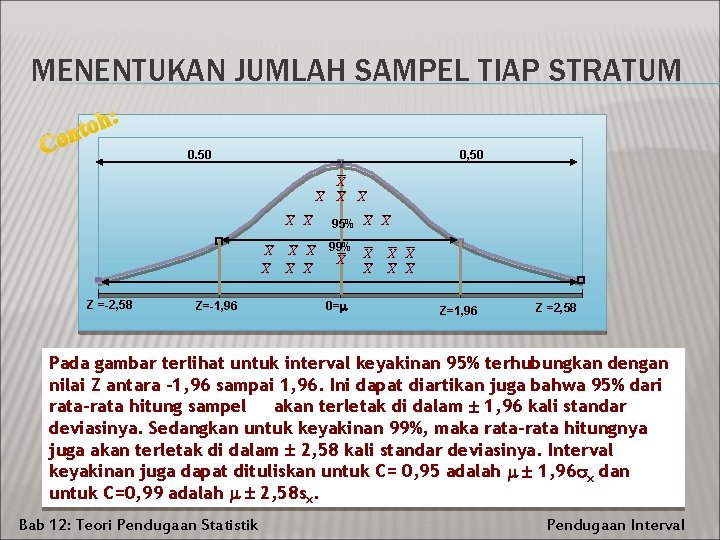
MENENTUKAN JUMLAH SAMPEL TIAP STRATUM : h o nt Co 0. 50 0, 50 X X X Z =-2, 58 Z=-1, 96 X X X 95% X X X 99% X X X 0= X X Z=1, 96 Z =2, 58 Pada gambar terlihat untuk interval keyakinan 95% terhubungkan dengan nilai Z antara – 1, 96 sampai 1, 96. Ini dapat diartikan juga bahwa 95% dari rata-rata hitung sampel akan terletak di dalam 1, 96 kali standar deviasinya. Sedangkan untuk keyakinan 99%, maka rata-rata hitungnya juga akan terletak di dalam 2, 58 kali standar deviasinya. Interval keyakinan juga dapat dituliskan untuk C= 0, 95 adalah 1, 96 x dan untuk C=0, 99 adalah 2, 58 sx. Bab 12: Teori Pendugaan Statistik Pendugaan Interval

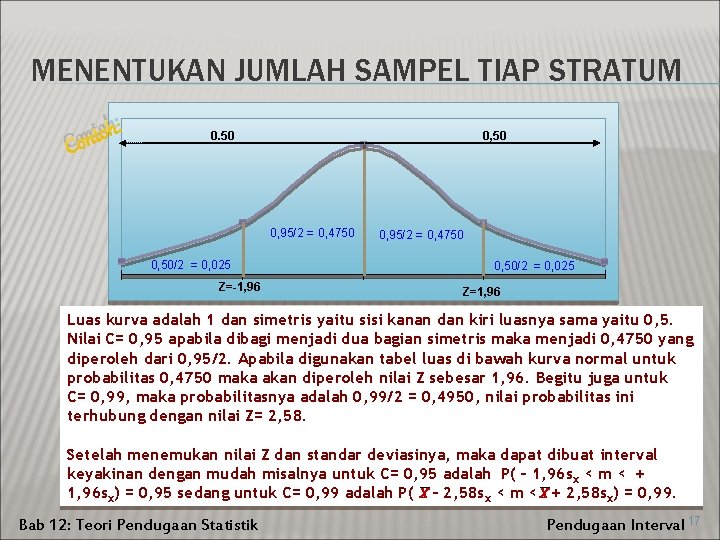
MENENTUKAN JUMLAH SAMPEL TIAP STRATUM : h o t on C 0. 50 0, 95/2 = 0, 4750 0, 50/2 = 0, 025 Z=-1, 96 0, 95/2 = 0, 4750 0, 50/2 = 0, 025 Z=1, 96 Luas kurva adalah 1 dan simetris yaitu sisi kanan dan kiri luasnya sama yaitu 0, 5. Nilai C= 0, 95 apabila dibagi menjadi dua bagian simetris maka menjadi 0, 4750 yang diperoleh dari 0, 95/2. Apabila digunakan tabel luas di bawah kurva normal untuk probabilitas 0, 4750 maka akan diperoleh nilai Z sebesar 1, 96. Begitu juga untuk C= 0, 99, maka probabilitasnya adalah 0, 99/2 = 0, 4950, nilai probabilitas ini terhubung dengan nilai Z= 2, 58. Setelah menemukan nilai Z dan standar deviasinya, maka dapat dibuat interval keyakinan dengan mudah misalnya untuk C= 0, 95 adalah P( – 1, 96 s x < m < + 1, 96 sx) = 0, 95 sedang untuk C= 0, 99 adalah P( X – 2, 58 sx < m < X + 2, 58 sx) = 0, 99. Bab 12: Teori Pendugaan Statistik Pendugaan Interval 17

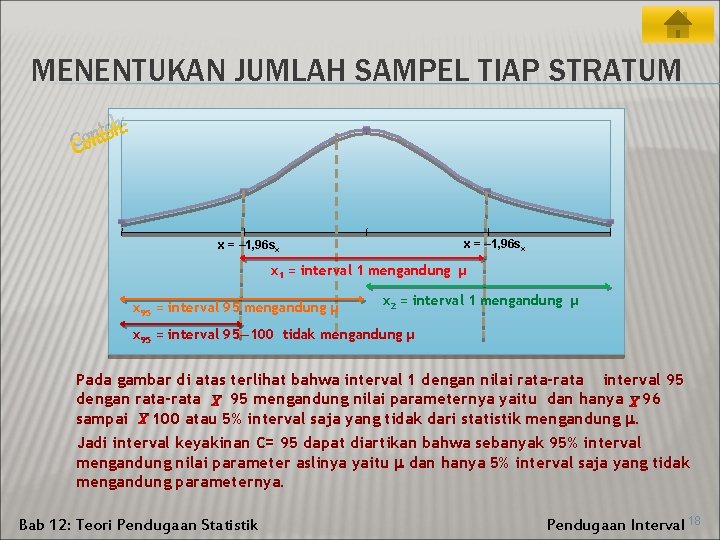
MENENTUKAN JUMLAH SAMPEL TIAP STRATUM h: o t n Co x = – 1, 96 sx x 1 = interval 1 mengandung µ x 95 = interval 95 mengandung µ x 2 = interval 1 mengandung µ x 95 = interval 95— 100 tidak mengandung µ Pada gambar di atas terlihat bahwa interval 1 dengan nilai rata-rata interval 95 dengan rata-rata X 95 mengandung nilai parameternya yaitu dan hanya X 96 sampai X 100 atau 5% interval saja yang tidak dari statistik mengandung . Jadi interval keyakinan C= 95 dapat diartikan bahwa sebanyak 95% interval mengandung nilai parameter aslinya yaitu dan hanya 5% interval saja yang tidak mengandung parameternya. Bab 12: Teori Pendugaan Statistik Pendugaan Interval 18

KESALAHAN STANDAR Kesalahan standar dari rata-rata hitung sampel adalah standar deviasi distribusi sampel dari rata-rata Bab 12: Teori Pendugaan Statistik Kesalahan Standar dari Rata-rata Hitung

RUMUS KESALAHAN STANDAR Untuk populasi yang tidak terbatas n/N < 0, 05: sx = n Untuk populasi yang terbatas n/N > 0, 05: sx = N - n n N -1 Bab 12: Teori Pendugaan Statistik : Standar deviasi populasi sx : Standar error/kesalahan standar dari rata-rata hitung sampel n : Jumlah atau ukuran sampel N : Jumlah atau ukuran populasi Kesalahan Standar dari Rata-rata Hitung 20

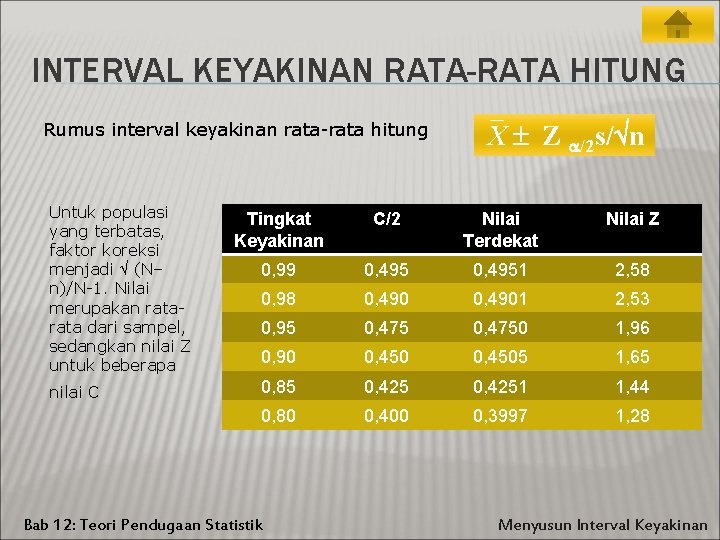
INTERVAL KEYAKINAN RATA-RATA HITUNG Rumus interval keyakinan rata-rata hitung Untuk populasi yang terbatas, faktor koreksi menjadi (N– n)/N-1. Nilai merupakan rata dari sampel, sedangkan nilai Z untuk beberapa nilai C X Z /2 s/ n Tingkat Keyakinan C/2 Nilai Terdekat Nilai Z 0, 99 0, 4951 2, 58 0, 98 0, 4901 2, 53 0, 95 0, 4750 1, 96 0, 90 0, 4505 1, 65 0, 85 0, 4251 1, 44 0, 80 0, 400 0, 3997 1, 28 Bab 12: Teori Pendugaan Statistik Menyusun Interval Keyakinan

INTERVAL KEYAKINAN RATA-RATA HITUNG Berdasarkan pada nilai Z dan diasumsikan bahwa n>30 maka dapat disusun interval beberapa keyakinan sebagai berikut: 99% • 2, 58 s/ n 98% • 2, 33 s/ n 95% • 1, 96 s/ n • 1, 65 s/ n • 1, 44 s/ n 99% 98% Bab 12: Teori Pendugaan Statistik 22 Menyusun Interval Keyakinan

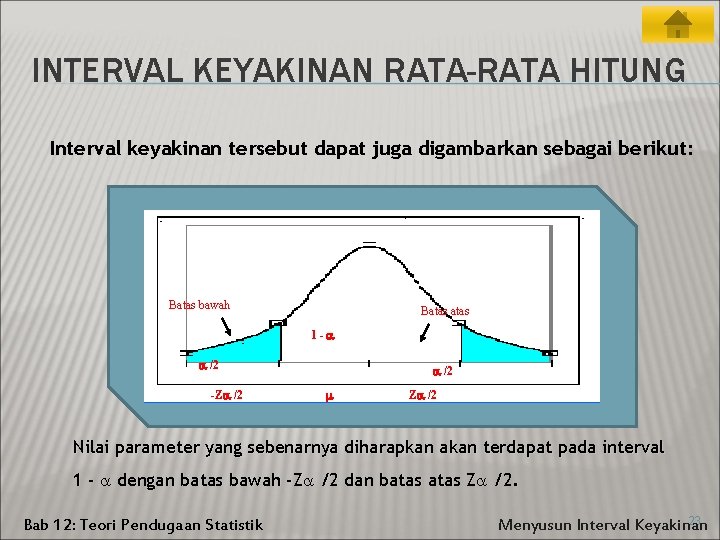
INTERVAL KEYAKINAN RATA-RATA HITUNG Interval keyakinan tersebut dapat juga digambarkan sebagai berikut: Batas bawah Batas 1 - /2 -Z /2 Nilai parameter yang sebenarnya diharapkan akan terdapat pada interval 1 - dengan batas bawah -Z /2 dan batas Z /2. Bab 12: Teori Pendugaan Statistik 23 Menyusun Interval Keyakinan

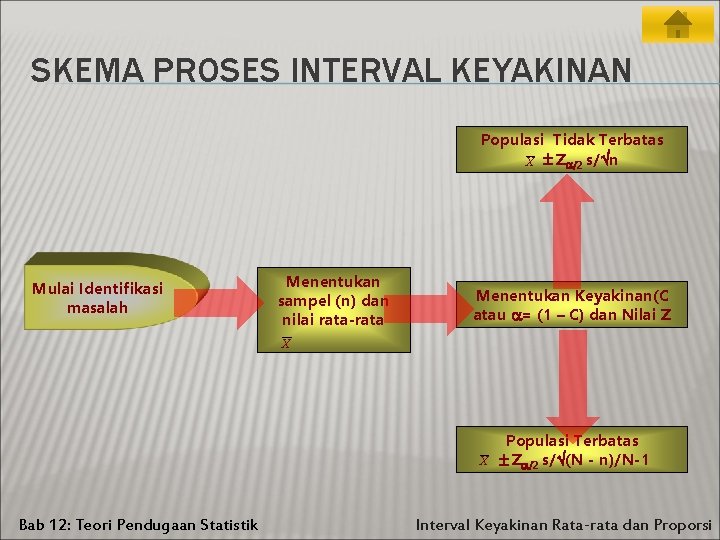
SKEMA PROSES INTERVAL KEYAKINAN Populasi Tidak Terbatas X Z /2 s/ n Mulai Identifikasi masalah Menentukan sampel (n) dan nilai rata-rata Menentukan Keyakinan(C atau = (1 – C) dan Nilai Z X X Bab 12: Teori Pendugaan Statistik Populasi Terbatas Z /2 s/ (N - n)/N-1 Interval Keyakinan Rata-rata dan Proporsi

DISTRIBUSI & STANDAR DEVIASI POPULASI Distribusi Sampling: Normal Standar Deviasi Populasi: Diketahui Probabilitas ( X – Z /2 x < < ( X Z /2 s/ (N – n)/N – 1 n sx ) = C atau X Probabilitas ( Z /2 sx ) = C : Rata-rata dari sampel Z /2 : Nilai Z dari tingkat kepercayaan : Rata-rata populasi yang diduga x : Standar error / kesalahan standar dari rata-rata hitung sampel C : Tingkat keyakinan : (1 – C) X Bab 12: Teori Pendugaan Statistik Interval Keyakinan Rata-rata dan Proporsi

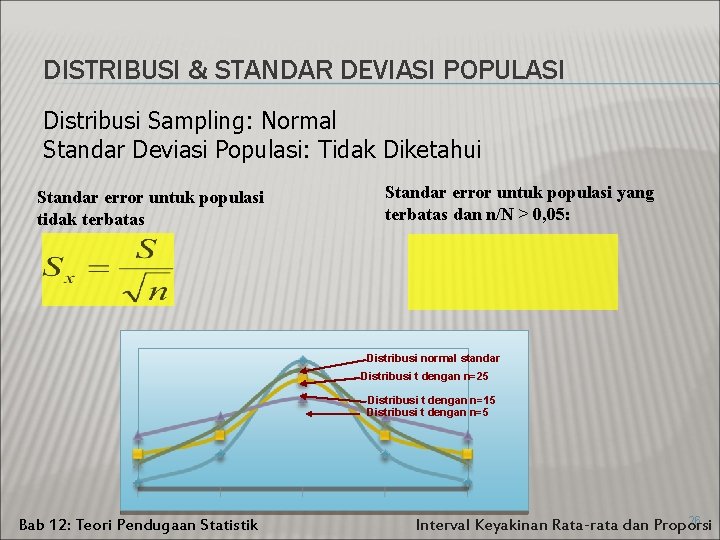
DISTRIBUSI & STANDAR DEVIASI POPULASI Distribusi Sampling: Normal Standar Deviasi Populasi: Tidak Diketahui Standar error untuk populasi tidak terbatas Standar error untuk populasi yang terbatas dan n/N > 0, 05: Distribusi normal standar Distribusi t dengan n=25 Distribusi t dengan n=15 Distribusi t dengan n=5 Bab 12: Teori Pendugaan Statistik 26 Interval Keyakinan Rata-rata dan Proporsi

DISTRIBUSI & STANDAR DEVIASI Distribusi Sampling: Mendekati Normal Standar Deviasi Populasi: Tidak Diketahui ( X – t /2 sx< < ( X + t /2 sx ) X : Rata-rata dari sampel t /2 : Nilai t dari tingkat kepercayaan : Rata-rata populasi yang diduga sx : Standar error/kesalahan standar dari rata-rata hitung sampel C : Tingkat keyakinan : 1–C Bab 12: Teori Pendugaan Statistik Interval Keyakinan Rata-rata dan Proporsi

DISTRIBUSI & STANDAR DEVIASI Untuk populasi yang tidak terbatas Untuk populasi yang terbatas Rumus pendugaan proporsi populasi Probabilitas (p - Z /2. Sp<P< p + Z /2. Sp) p : Proporsi sampel Z /2: Nilai Z dari tingkat keyakinan P : Proporsi populasi yang diduga Sp : Standar error/kesalahan dari proporsi C : Tingkat keyakinan : 1 – C Bab 12: Teori Pendugaan Statistik 28 Interval Keyakinan Rata-rata dan Proporsi

INTERVAL KEYAKINAN UNTUK SELISIH RATA-RATA Probabilitas (( X 1 - X)2 - Z /2. x 1 -x 2) < ( - X 1 ) <X 2 ( - )X 1+ ZX /2 2. x 1 -x 2) Di mana standar error dari nilai selisih rata-rata adalah: Apabila standar deviasi dari populasi tidak ada, maka dapat diduga dengan standar deviasi sampel yaitu: Di mana: x 1 -x 2 : Standar deviasi selisih rata-rata populasi sx 1 -x 2 : Standar error selisih rata-rata sx 1, sx 1: Standar deviasi sampel dari dua populasi n 1, n 2: Jumlah sampel setiap populasi Bab 12: Teori Pendugaan Statistik Interval Keyakinan Rata-rata Selisih dan

INTERVAL KEYAKINAN UNTUK SELISIH PROPORSI Probabilitas ((p 1 -p 2) - Z /2. sp 1 -p 2) <(P 1 -P 2) < (p 1 -p 2) + Z /2. sp 1 -p 2) Di mana standar error dari nilai selisih proporsi adalah: p 1, p 2 : Proporsi sampel dari dua populasi Sp 1, sp 1: Standar error selisih proporsi dari dua populasi n 1, n 2 : Jumlah sampel setiap populasi Bab 12: Teori Pendugaan Statistik Interval Keyakinan Rata-rata Selisih dan

FAKTOR UKURAN SAMPEL Faktor yang memengaruhi jumlah sampel: Tingkat keyakinan yang dipilih Kesalahan maksimum yang diperbolehkan Variasi dari populasi Bab 12: Teori Pendugaan Statistik 31 Memilih Ukuran Sampel

RUMUS JUMLAH SAMPEL UNTUK MENDUGA RATA-RATA POPULASI Rumus jumlah sampel dalam populasi dirumuskan sebagai berikut: n = [(Za/2. s)/e]2 Rumus tersebut diturunkan dari interval keyakinan sebagaimana diuraikan sebagai berikut: P (–Za/2 < Za/2 ) = C = 1 – a (–Za/2 < ( – m)/(s/Ön) < Za/2) (–Za/2 (s/Ön) < ( – m) < Za/2(s/Ön)) (x – m) < Za/2(s/Ön); ingat bahwa error e = – m e < Za/2(s/Ön); e 2 = (Za/2)2(s 2/n); n = [(Za/2. s)/e]2 Bab 12: Teori Pendugaan Statistik 32 Memilih Ukuran Sampel

RUMUS JUMLAH SAMPEL UNTUK MENDUGA RATA-RATA POPULASI Untuk mendapatkan rumus jumlah sampel dalam pendugaan proporsi populasi dapat diturunkan sebagai berikut: P (–Z /2 < Z /2 ) = C = 1 – (–Z /2 < (p 1 – p 2)/( / n) <Z /2) (–Z /2( [(p(1 – p)]/n – 1) < (p 1 – p 2) < Z /2( [p(1– p)]/n– 1) (p 1 – p 2) < Z /2( [(p(1 – p)]/n – 1); ingat bahwa error e = p 1 – p 2 e < Z /2( [(p(1 – p)]/n – 1); dikuadratkan kedua sisi menjadi e 2 = (Z /2)2[(p(1 – p)]/n – 1; dipindahkan n – 1 ke sisi kiri n – 1 = (Z /2. )2 p(1 – p) sehingga n menjadi e 2 n = (Z /2. )2 p(1 – p) + 1 e 2 Bab 12: Teori Pendugaan Statistik 33 Memilih Ukuran Sampel

T A K E M A H R I S I 34
 Penduga selang adalah
Penduga selang adalah Sel adalah pertemuan antara titik-titik dan titik-titik
Sel adalah pertemuan antara titik-titik dan titik-titik Campuran homogen tersusun dari titik-titik dan titik-titik
Campuran homogen tersusun dari titik-titik dan titik-titik Yang merupakan jenis-jenis pendugaan parameter adalah
Yang merupakan jenis-jenis pendugaan parameter adalah Pendugaan rasio dua ragam
Pendugaan rasio dua ragam Pendugaan adalah
Pendugaan adalah Jenis jenis pendugaan
Jenis jenis pendugaan Rumus pendugaan titik
Rumus pendugaan titik Contoh pendugaan titik
Contoh pendugaan titik Tentukanlah nilai yang dikosongkan berikut ini
Tentukanlah nilai yang dikosongkan berikut ini Etika dasar desain grafis
Etika dasar desain grafis Peta konsep komponen komputer
Peta konsep komponen komputer Konsep dasar unit pemrosesan dan dasar datapath
Konsep dasar unit pemrosesan dan dasar datapath Organisasi datapath
Organisasi datapath Pengertian profesi kependidikan
Pengertian profesi kependidikan Peta konsep materi peluang kelas 12
Peta konsep materi peluang kelas 12 Pengertian komunikasi
Pengertian komunikasi Perbedaan fbm dan abm
Perbedaan fbm dan abm Konsep konsep dasar kewirausahaan
Konsep konsep dasar kewirausahaan Apakah manfaat membaca senyap
Apakah manfaat membaca senyap Tambahkanlah
Tambahkanlah Contoh varian pemrograman
Contoh varian pemrograman We... to the college yesterday
We... to the college yesterday Andi memiliki tangki minyak berbentuk tabung
Andi memiliki tangki minyak berbentuk tabung Software pengolah gambar bitmap
Software pengolah gambar bitmap Lagu satu satu aku sayang ibu ciptaan
Lagu satu satu aku sayang ibu ciptaan Angka ketelitian yang dimiliki oleh jangka sorong adalah
Angka ketelitian yang dimiliki oleh jangka sorong adalah Titik l terletak pada koordinat
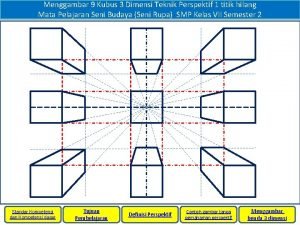
Titik l terletak pada koordinat Perspektif lemari
Perspektif lemari Eko is titik-titik dan ari
Eko is titik-titik dan ari Kukenang jasamu pembela nusa bangsa
Kukenang jasamu pembela nusa bangsa Lempeng prisma tiang granular merupakan titik-titik tanah
Lempeng prisma tiang granular merupakan titik-titik tanah Tanda titik digunakan untuk
Tanda titik digunakan untuk Panjang pr qr 13 cm dan pq 10 cm maka panjang rs adalah
Panjang pr qr 13 cm dan pq 10 cm maka panjang rs adalah Gambarkan bangun datar persegi tunjukkan dengan garis tebal
Gambarkan bangun datar persegi tunjukkan dengan garis tebal