1 Outline Introduction Background Distributed Database Design Database

1 Outline Introduction Background Distributed Database Design Database Integration Semantic Data Control Distributed Query Processing Overview Query decomposition and localization Distributed query optimization Multidatabase query processing Distributed Transaction Management Data Replication Parallel Database Systems Distributed Object DBMS Peer-to-Peer Data Management Web Data Management Current Issues

Query Optimization Issues – 2 Replicated Fragments A distributed relation is usually divided into relation fragments. Localization: Distributed queries expressed on global relations are mapped into queries on physical fragments of relations by translating relations into fragments.

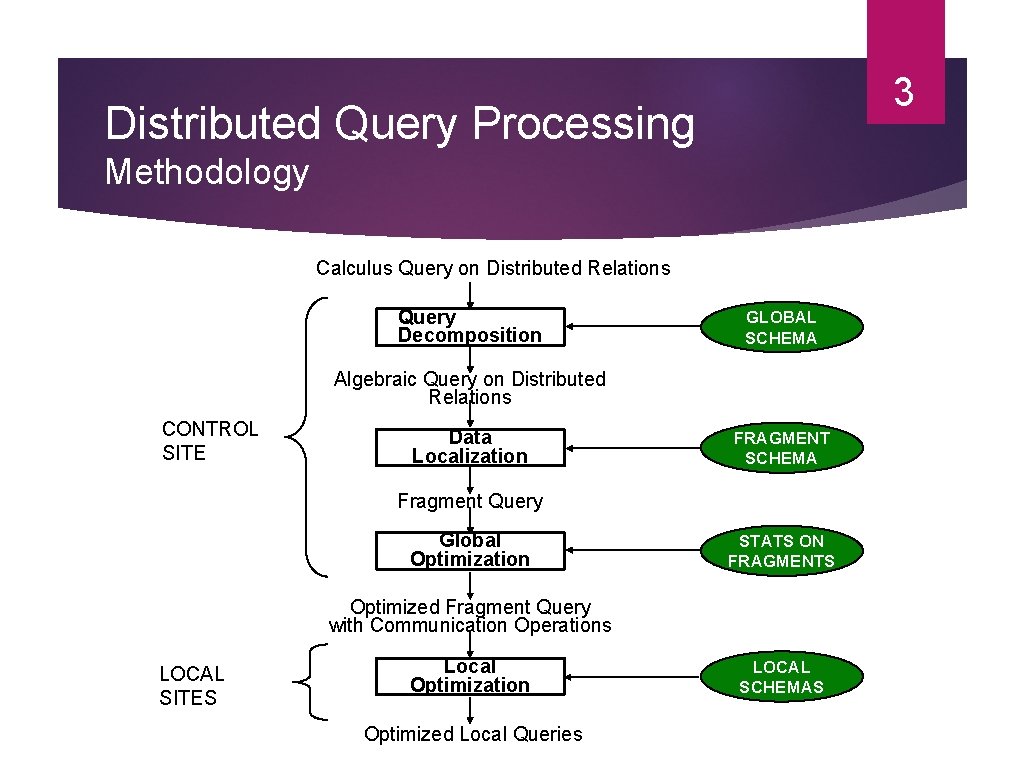
3 Distributed Query Processing Methodology Calculus Query on Distributed Relations Query Decomposition GLOBAL SCHEMA Algebraic Query on Distributed Relations CONTROL SITE Data Localization FRAGMENT SCHEMA Fragment Query Global Optimization STATS ON FRAGMENTS Optimized Fragment Query with Communication Operations LOCAL SITES Local Optimization Optimized Local Queries LOCAL SCHEMAS

4 Step 1 – Query Decomposition Input : Calculus query on global relations Process: 1) Normalization manipulate query quantifiers and qualification 2) Analysis detect and reject “incorrect” queries possible for only a subset of relational calculus 3) Simplification 4) eliminate redundant predicates Restructuring calculus query algebraic query NOTE: More than one translation may be possible. use transformation rules

5 Normalization Lexical and syntactic analysis check validity (similar to compilers) check for attributes and relations type checking on the qualification Put into normal form Conjunctive normal form (p 11 p 12 … p 1 n) … (pm 1 pm 2 … pmn) Disjunctive normal form (p 11 p 12 … p 1 n) … (pm 1 pm 2 … pmn) OR's mapped into union AND's mapped into join or selection

6 Analysis Refute incorrect queries Type incorrect If any of its attribute or relation names are not defined in the global schema If operations are applied to attributes of the wrong type Semantically incorrect Components do not contribute in any way to the generation of the result Only a subset of relational calculus queries can be tested for correctness Those that do not contain disjunction and negation To detect connection graph (query graph) join graph

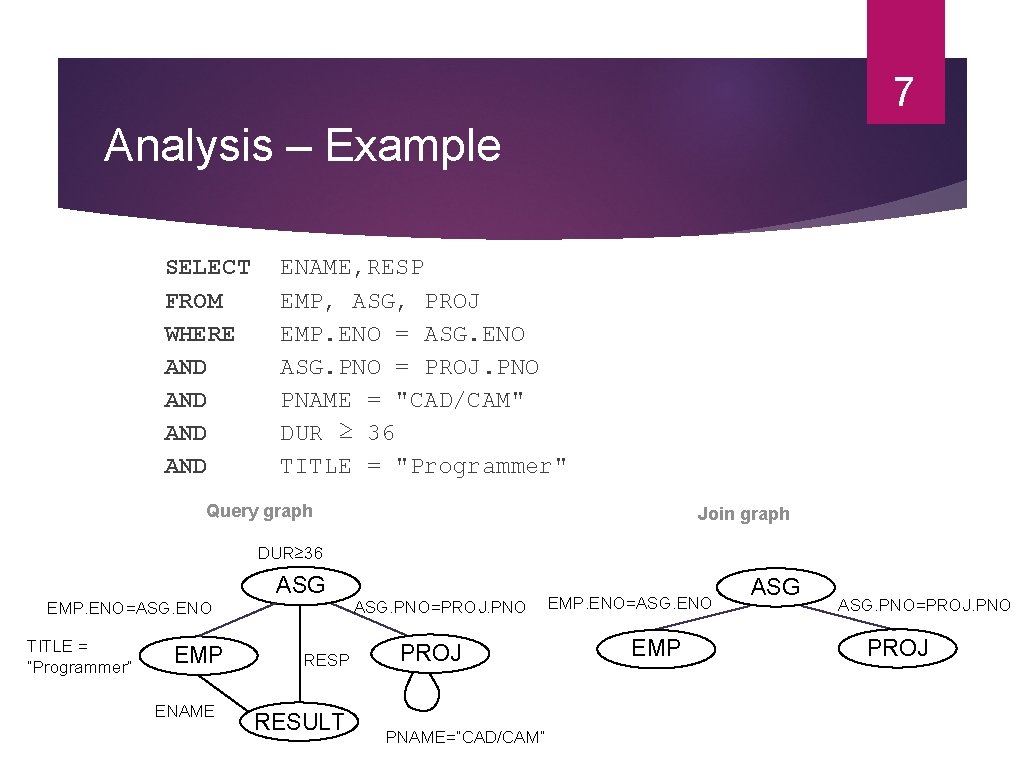
7 Analysis – Example SELECT FROM WHERE AND AND ENAME, RESP EMP, ASG, PROJ EMP. ENO = ASG. ENO ASG. PNO = PROJ. PNO PNAME = "CAD/CAM" DUR ≥ 36 TITLE = "Programmer" Query graph Join graph DUR≥ 36 ASG EMP. ENO=ASG. ENO TITLE = “Programmer” EMP ENAME RESP RESULT ASG. PNO=PROJ. PNO PROJ PNAME=“CAD/CAM” EMP. ENO=ASG. ENO EMP ASG. PNO=PROJ. PNO PROJ

8 Analysis If the query graph is not connected, the query may be wrong or use Cartesian product. SELECT ENAME, RESP FROM EMP, ASG, PROJ WHERE EMP. ENO = ASG. ENO AND PNAME = "CAD/CAM" AND DUR > 36 AND TITLE = "Programmer" ASG EMP ENAME RESP RESULT PROJ PNAME=“CAD/CAM”

9 Simplification Why simplify? Remember the example How? Use transformation rules Elimination of redundancy idempotency rules Application of transitivity Use of integrity rules

10 Simplification – Example SELECT FROM WHERE OR AND TITLE EMP. ENAME = "J. Doe" (NOT(EMP. TITLE = "Programmer") (EMP. TITLE = "Programmer" EMP. TITLE = "Elect. Eng. ") NOT(EMP. TITLE = "Elect. Eng. ")) SELECT FROM WHERE TITLE EMP. ENAME = "J. Doe"

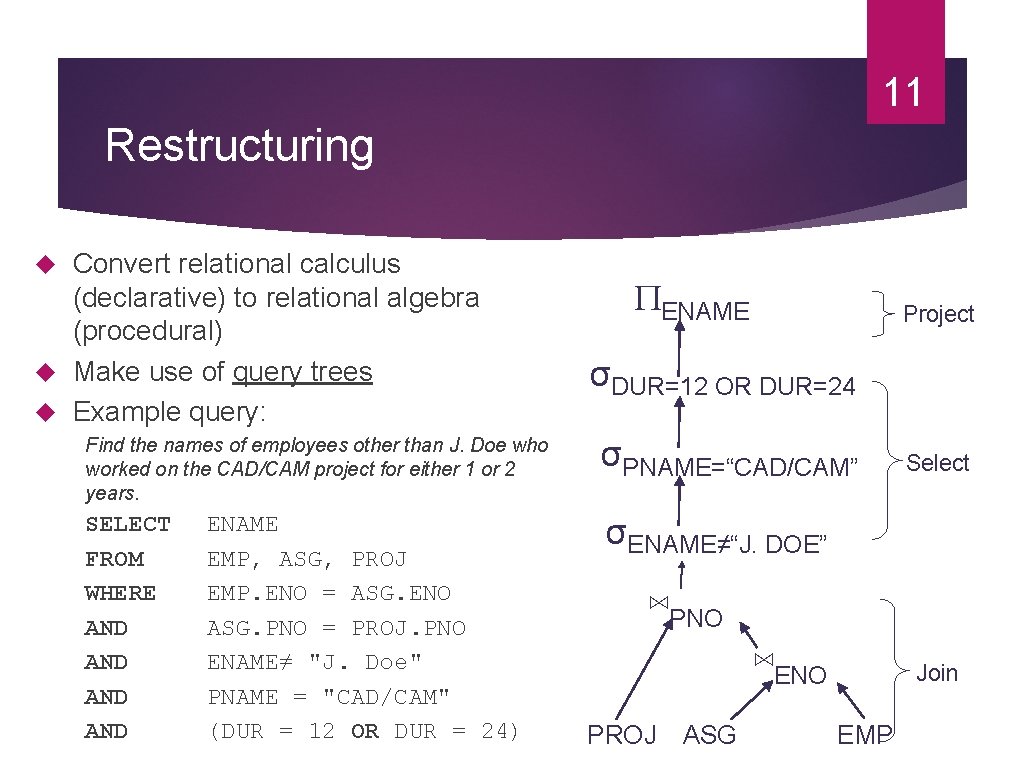
11 Restructuring Convert relational calculus (declarative) to relational algebra (procedural) Make use of query trees Example query: ENAME Project σDUR=12 OR DUR=24 Find the names of employees other than J. Doe who worked on the CAD/CAM project for either 1 or 2 years. σPNAME=“CAD/CAM” SELECT FROM WHERE AND AND σENAME≠“J. DOE” ENAME EMP, ASG, PROJ EMP. ENO = ASG. ENO ASG. PNO = PROJ. PNO ENAME≠ "J. Doe" PNAME = "CAD/CAM" (DUR = 12 OR DUR = 24) Select ⋈PNO ⋈ENO PROJ ASG Join EMP

Restructuring – Transformation Rules Commutativity of binary operations R×S S× R R ⋈S S ⋈R R S S R Associativity of binary operations ( R × S) × T R × (S × T) (R ⋈S) ⋈T R ⋈ (S ⋈T) Idempotence of unary operations A’( A’’(R)) A’(R) p 1(A 1)( p 2(A 2)(R)) p 1(A 1) p 2(A 2)(R) where R[A] and A' A, A" A and A' A" Commuting selection with projection 12

Restructuring – Transformation Rules Commuting selection with binary operations p(A)(R × S) ( p(A) (R)) × S p(A )(R ⋈(A , B )S) ( p(A ) (R)) ⋈(A , B )S i j k p(A )(R T) p(A ) (R) p(A ) (T) i i i where Ai belongs to R and T Commuting projection with binary operations C(R × S) A’(R) × B’(S) C(R ⋈(A , B )S) A’(R) ⋈(A , B ) B’(S) j k C(R S) C(R) C(S) where R[A] and S[B]; C = A' B' where A' A, B' B 13

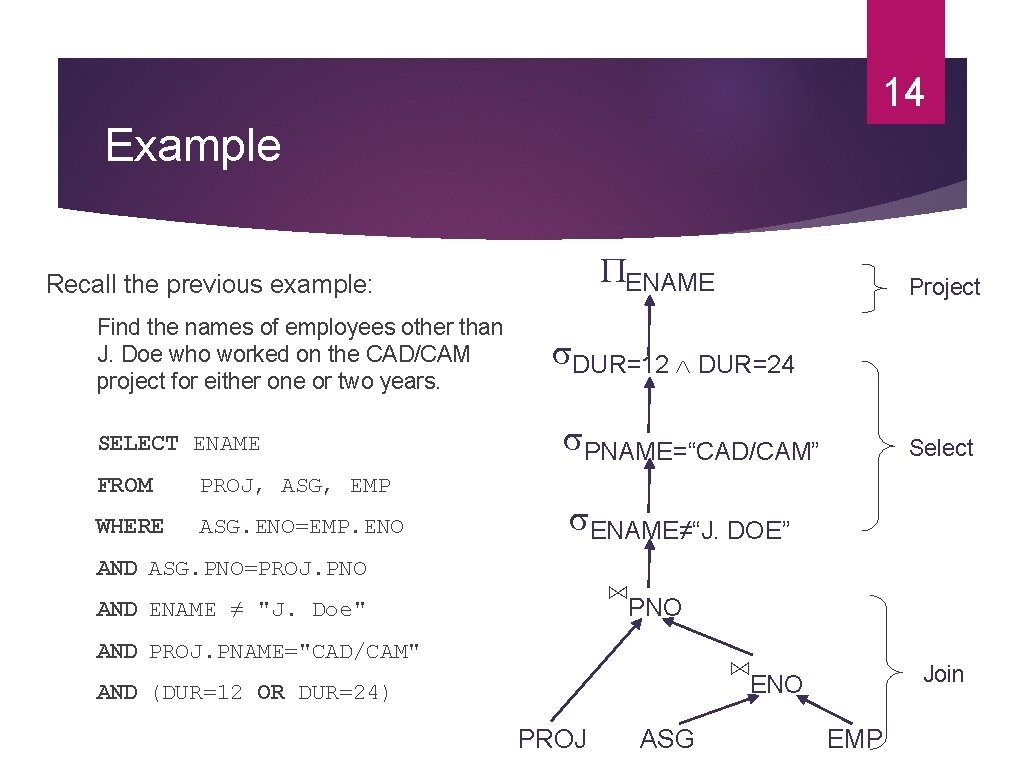
14 Example ENAME Recall the previous example: Find the names of employees other than J. Doe who worked on the CAD/CAM project for either one or two years. SELECT ENAME FROM PROJ, ASG, EMP WHERE ASG. ENO=EMP. ENO Project DUR=12 DUR=24 PNAME=“CAD/CAM” Select ENAME≠“J. DOE” AND ASG. PNO=PROJ. PNO ⋈PNO AND ENAME ≠ "J. Doe" AND PROJ. PNAME="CAD/CAM" ⋈ENO AND (DUR=12 OR DUR=24) PROJ ASG Join EMP

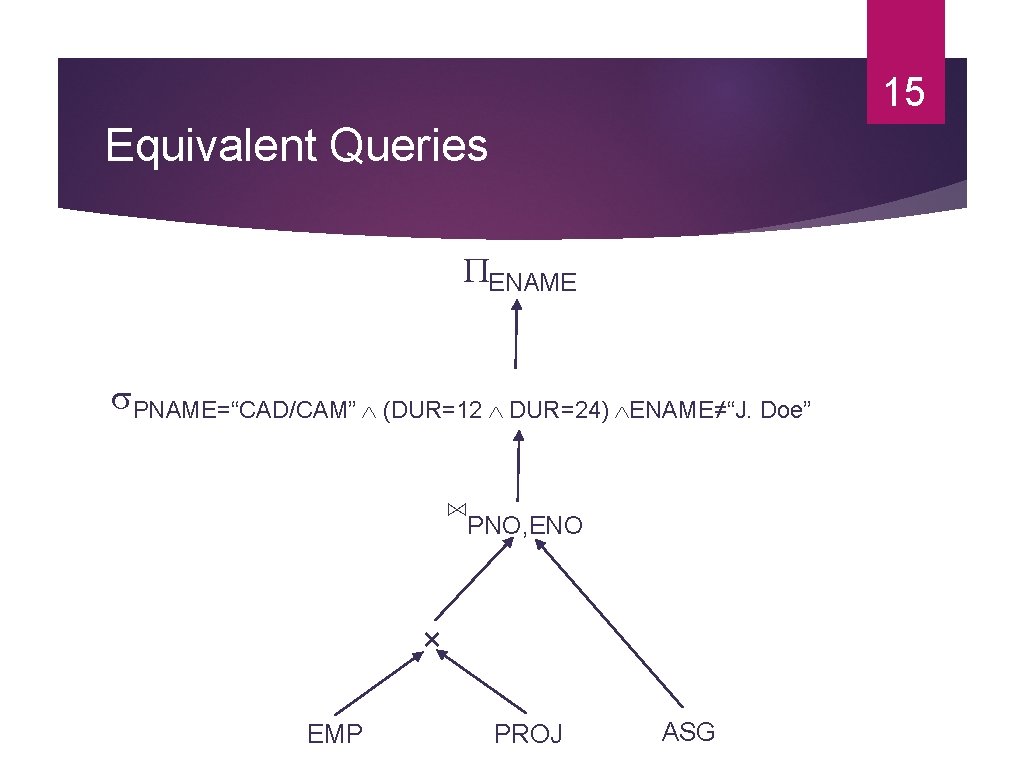
15 Equivalent Queries ENAME PNAME=“CAD/CAM” (DUR=12 DUR=24) ENAME≠“J. Doe” ⋈PNO, ENO × EMP PROJ ASG

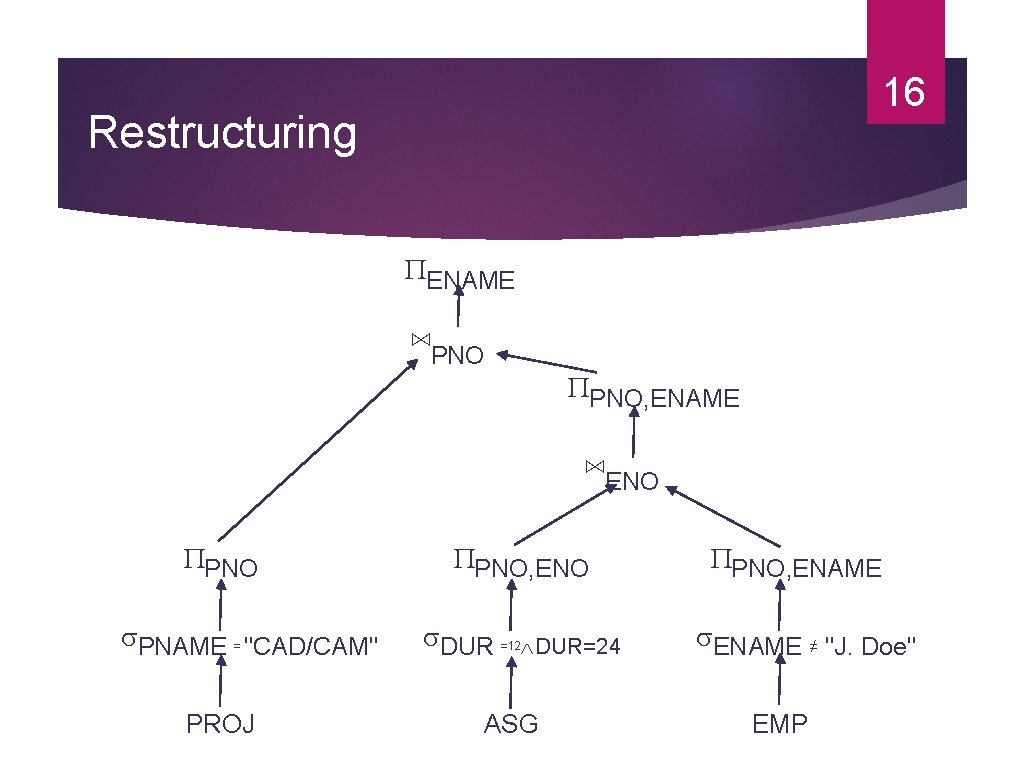
16 Restructuring ENAME ⋈PNO PNO, ENAME ⋈ENO PNAME = "CAD/CAM" PROJ PNO, ENO DUR =12 DUR=24 ASG PNO, ENAME ≠ "J. Doe" EMP

17 Step 2 – Data Localization Input: Algebraic query on distributed relations Process: Determine which fragments are involved Localization program substitute for each global query its materialization program optimize

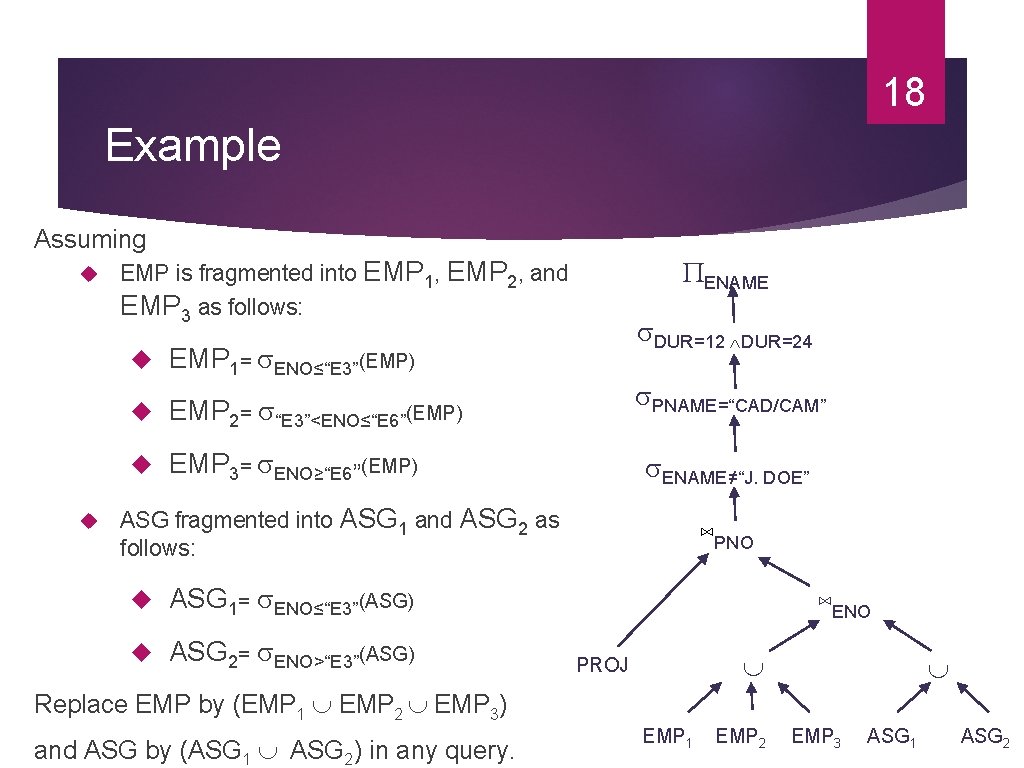
18 Example Assuming ENAME EMP is fragmented into EMP 1, EMP 2, and EMP 3 as follows: DUR=12 DUR=24 EMP 1= ENO≤“E 3”(EMP) EMP 2= “E 3”<ENO≤“E 6”(EMP) EMP 3= ENO≥“E 6”(EMP) PNAME=“CAD/CAM” ENAME≠“J. DOE” ASG fragmented into ASG 1 and ASG 2 as follows: ASG 1= ENO≤“E 3”(ASG) ASG 2= ENO>“E 3”(ASG) ⋈PNO ⋈ENO PROJ Replace EMP by (EMP 1 EMP 2 EMP 3) and ASG by (ASG 1 ASG 2) in any query. EMP 1 EMP 2 EMP 3 ASG 1 ASG 2

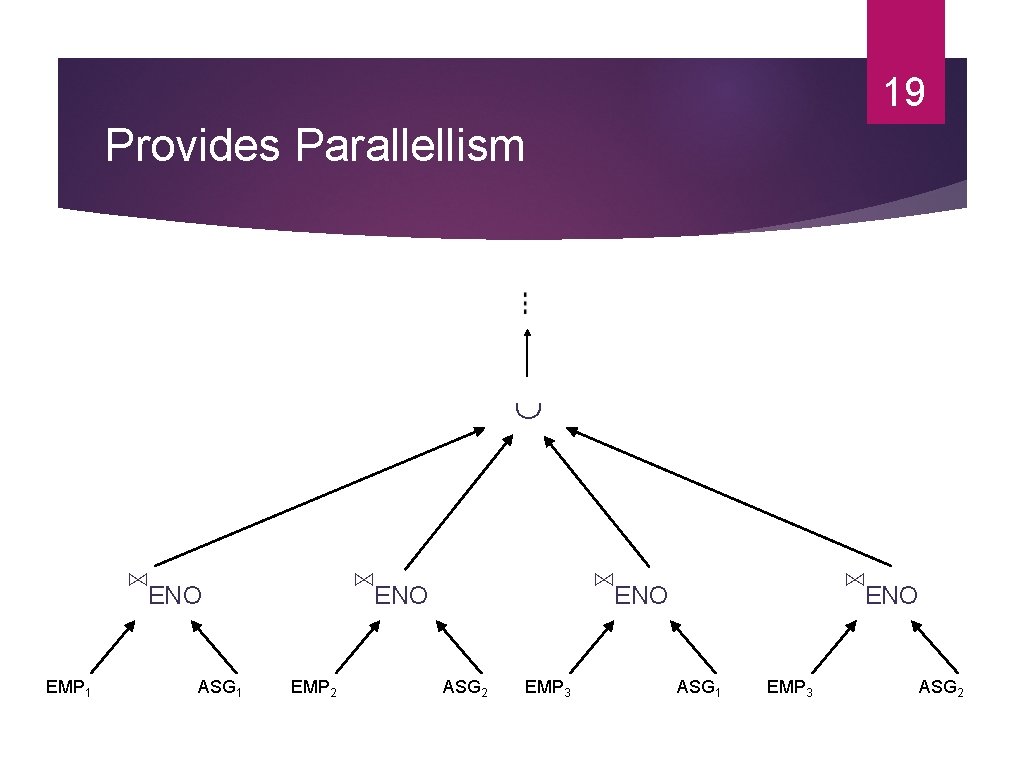
19 Provides Parallellism ⋈ENO EMP 1 ASG 1 ⋈ENO EMP 2 ⋈ENO ASG 2 EMP 3 ⋈ENO ASG 1 EMP 3 ASG 2

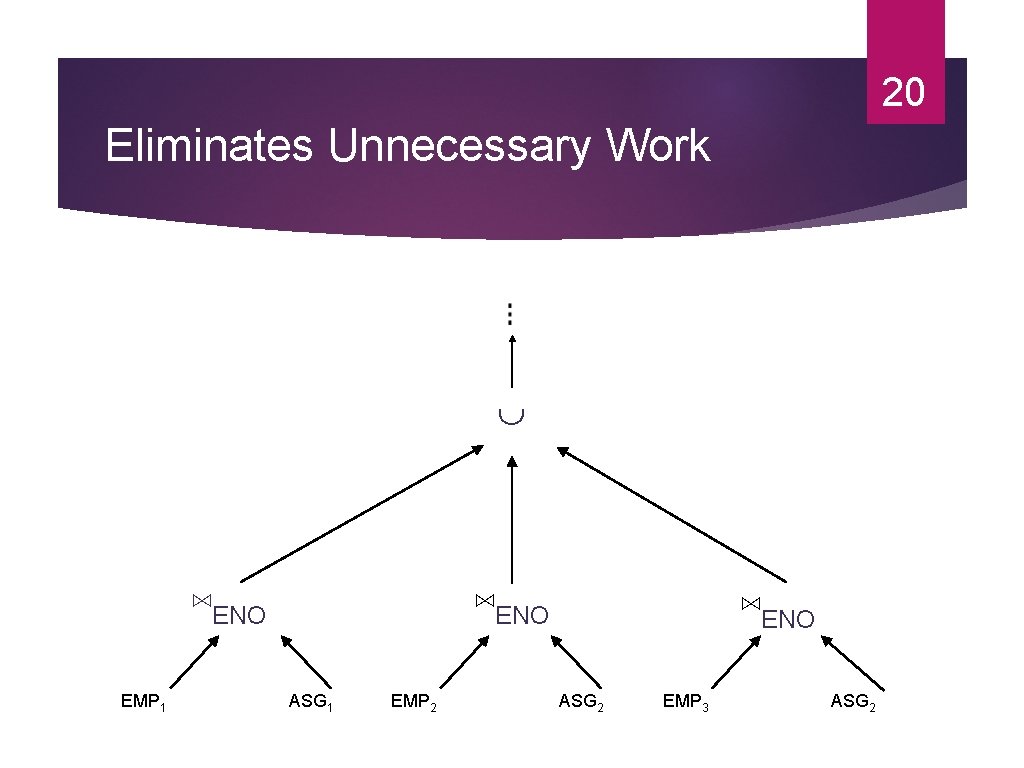
20 Eliminates Unnecessary Work ⋈ENO EMP 1 ⋈ENO ASG 1 EMP 2 ⋈ENO ASG 2 EMP 3 ASG 2

21 Reduction for Primary Horizontal Fragmentation (PHF) Reduction with selection Relation R and FR={R 1, R 2, …, Rw} where Rj= pj(R) pi(Rj)= if x in R: ¬(pi(x) pj(x)) Example ENO=“E 5” SELECT * FROM EMP WHERE ENO="E 5" ENO=“E 5” EMP 1 EMP 2 EMP 3 EMP 2

22 Reduction for PHF Reduction with join Possible if fragmentation is done on join attribute Distribute join over union (R 1 R 2)⋈S (R 1⋈S) (R 2⋈S) Given Ri = pi(R) and Rj = pj(R) R⋈i Rj = if x in Ri, y in Rj: ¬(pi(x) pj(y))

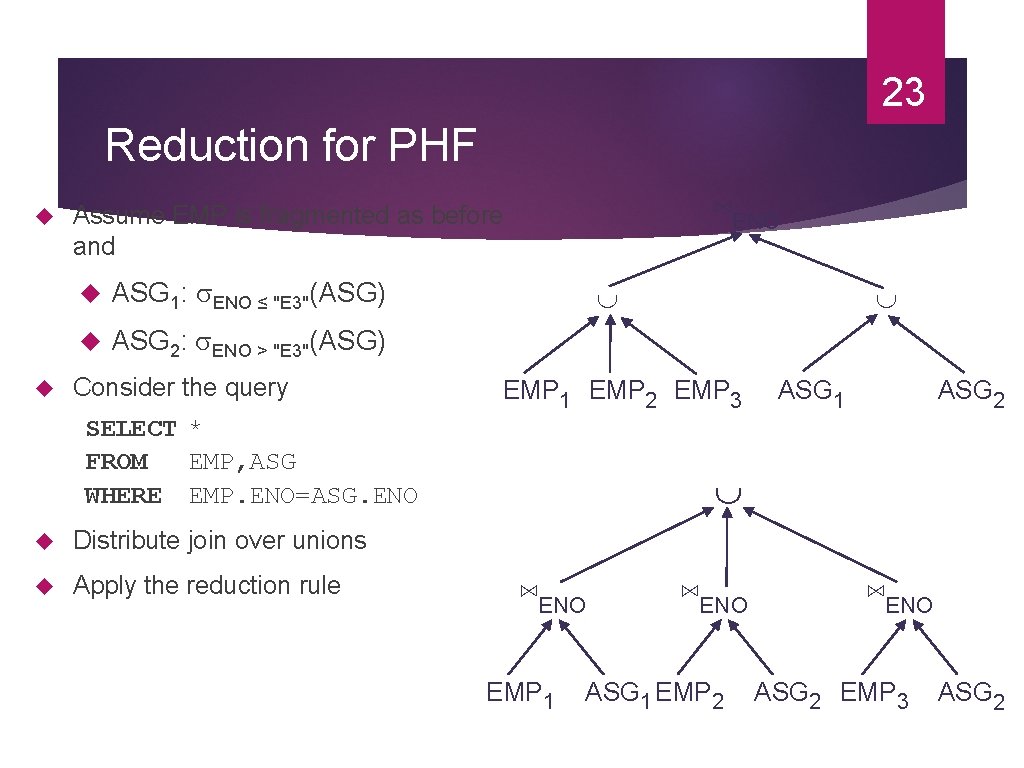
23 Reduction for PHF ⋈ENO Assume EMP is fragmented as before and ASG 1: ENO ≤ "E 3"(ASG) ASG 2: ENO > "E 3"(ASG) Consider the query EMP 1 EMP 2 EMP 3 SELECT * FROM EMP, ASG WHERE EMP. ENO=ASG. ENO Distribute join over unions Apply the reduction rule ASG 1 ASG 2 ⋈ENO EMP 1 ⋈ENO ASG 1 EMP 2 ⋈ENO ASG 2 EMP 3 ASG 2

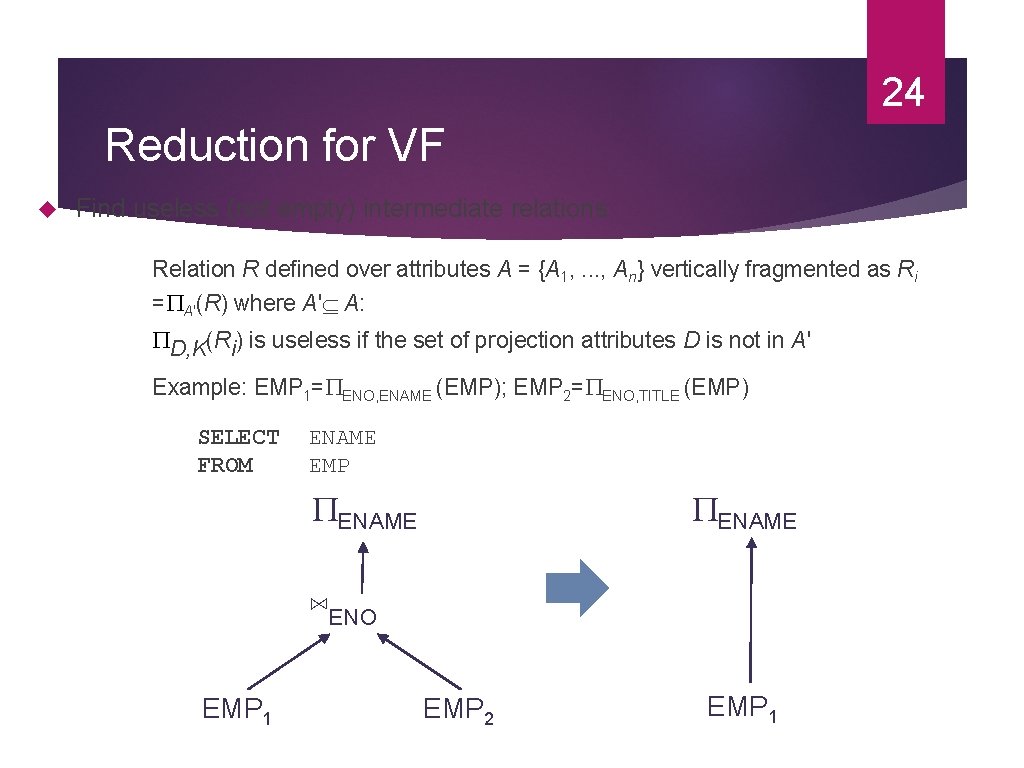
24 Reduction for VF Find useless (not empty) intermediate relations Relation R defined over attributes A = {A 1, . . . , An} vertically fragmented as Ri = A'(R) where A' A: D, K(Ri) is useless if the set of projection attributes D is not in A' Example: EMP 1= ENO, ENAME (EMP); EMP 2= ENO, TITLE (EMP) SELECT FROM ENAME EMP ENAME ⋈ENO EMP 1 EMP 2 EMP 1

25 Reduction for DHF Rule : Distribute joins over unions Apply the join reduction for horizontal fragmentation Example ASG 1: ASG ⋉ENO EMP 1 ASG 2: ASG ⋉ENO EMP 2 EMP 1: TITLE=“Programmer” (EMP) EMP 2: TITLE=“Programmer” (EMP) Query SELECT * FROM EMP, ASG WHERE ASG. ENO = EMP. ENO AND EMP. TITLE = "Mech. Eng. "

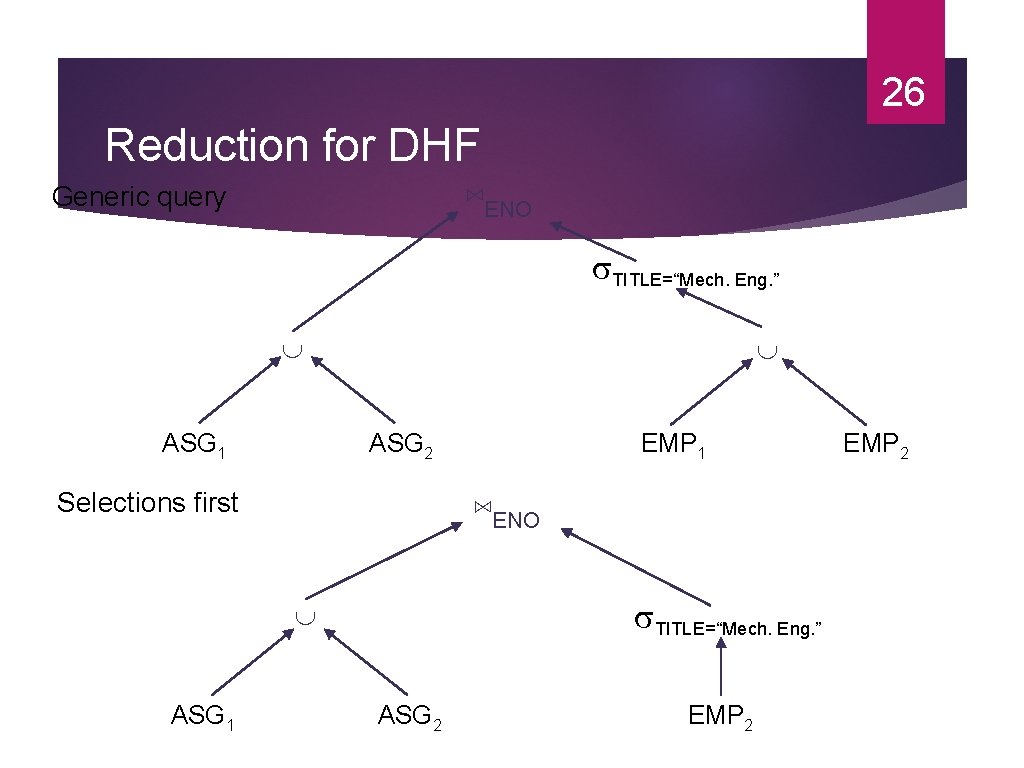
26 Reduction for DHF ⋈ENO Generic query TITLE=“Mech. Eng. ” ASG 1 ASG 2 Selections first ⋈ENO TITLE=“Mech. Eng. ” ASG 1 EMP 1 ASG 2 EMP 2

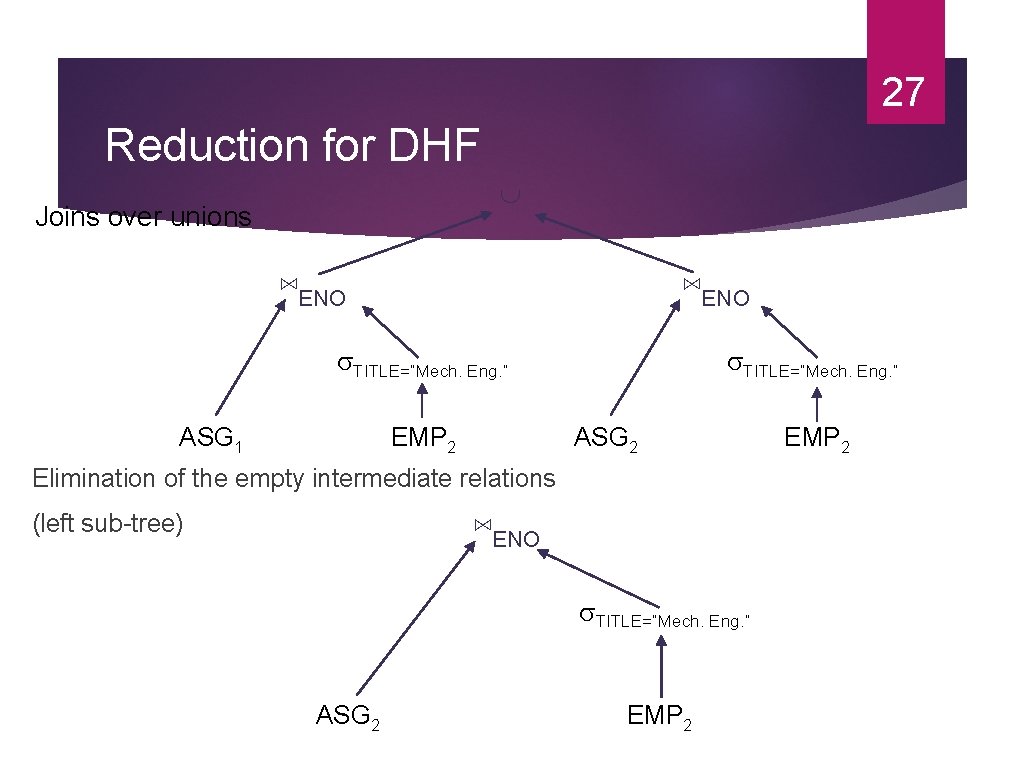
27 Reduction for DHF Joins over unions ⋈ENO TITLE=“Mech. Eng. ” ASG 1 EMP 2 TITLE=“Mech. Eng. ” ASG 2 Elimination of the empty intermediate relations ⋈ENO (left sub-tree) TITLE=“Mech. Eng. ” ASG 2 EMP 2

Reduction for Hybrid Fragmentation Combine the rules already specified: Remove empty relations generated by contradicting selections on horizontal fragments; Remove useless relations generated by projections on vertical fragments; Distribute joins over unions in order to isolate and remove useless joins. 28

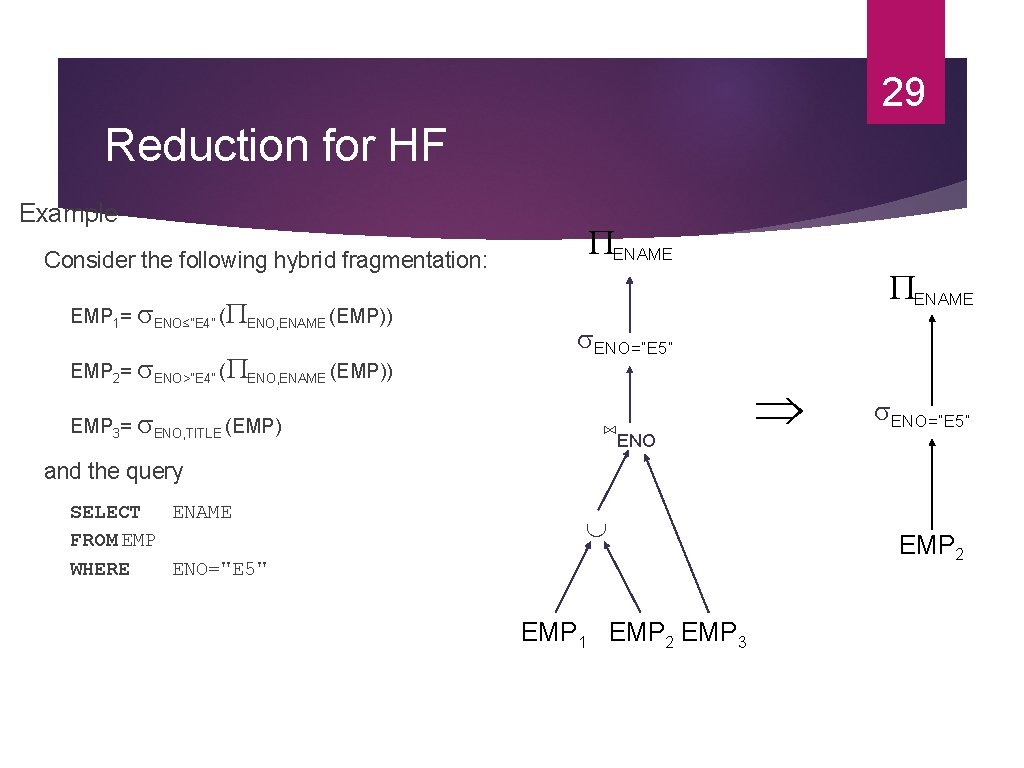
29 Reduction for HF Example Consider the following hybrid fragmentation: EMP 1= ENO≤"E 4" ( ENO, ENAME (EMP)) EMP 2= ENO>"E 4" ( ENO, ENAME (EMP)) EMP 3= ENO, TITLE (EMP) ENAME ENO=“E 5” ⋈ENO ENO=“E 5” and the query SELECT ENAME FROM EMP WHERE ENO="E 5" EMP 1 EMP 2 EMP 3 EMP 2