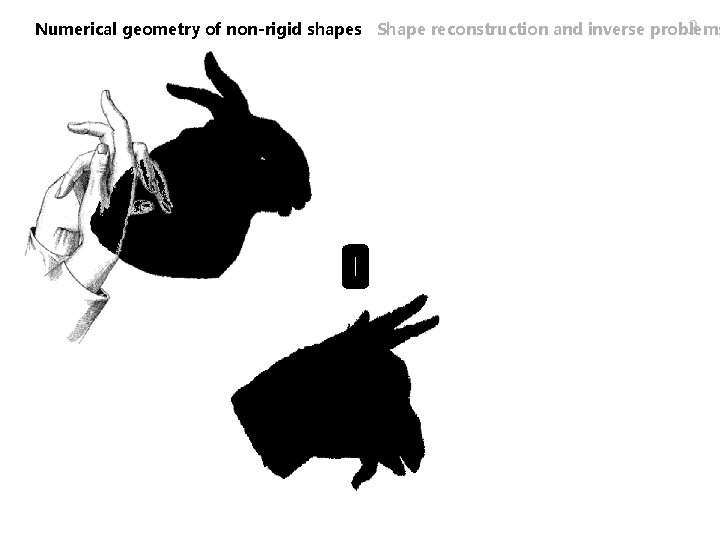
1 Numerical geometry of nonrigid shapes Shape reconstruction

1 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Lecture 9 © Alexander & Michael Bronstein tosca. cs. technion. ac. il/book Numerical geometry of non-rigid shapes Stanford University, Winter 2009

2 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems

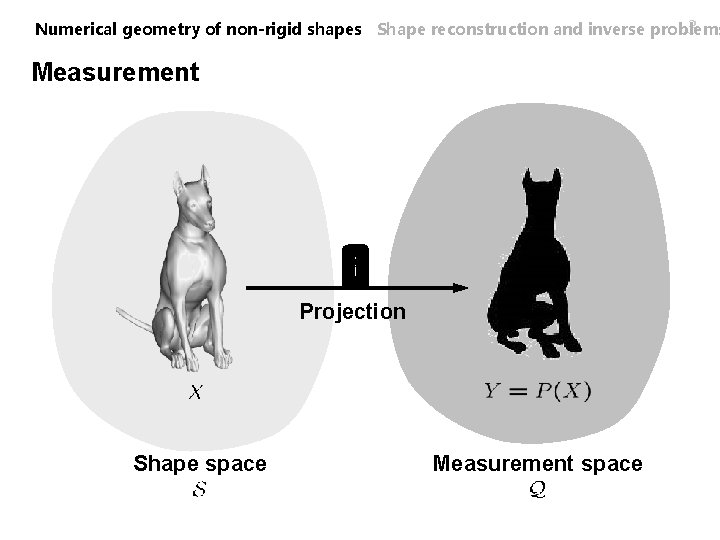
3 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Measurement Projection Shape space Measurement space

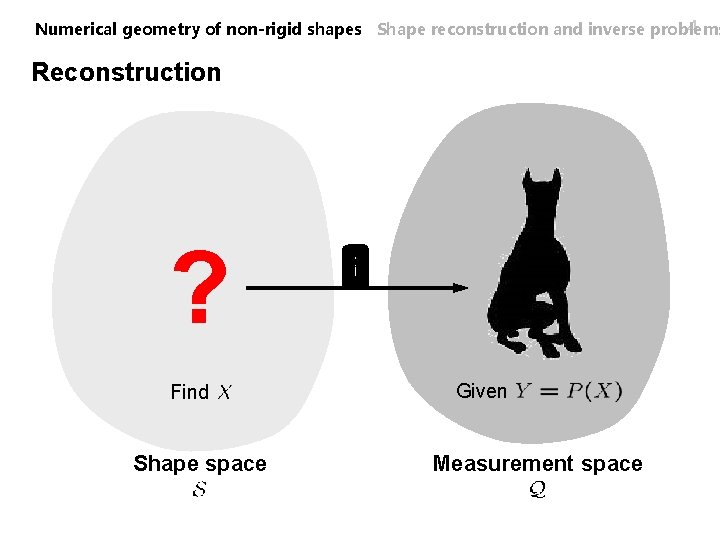
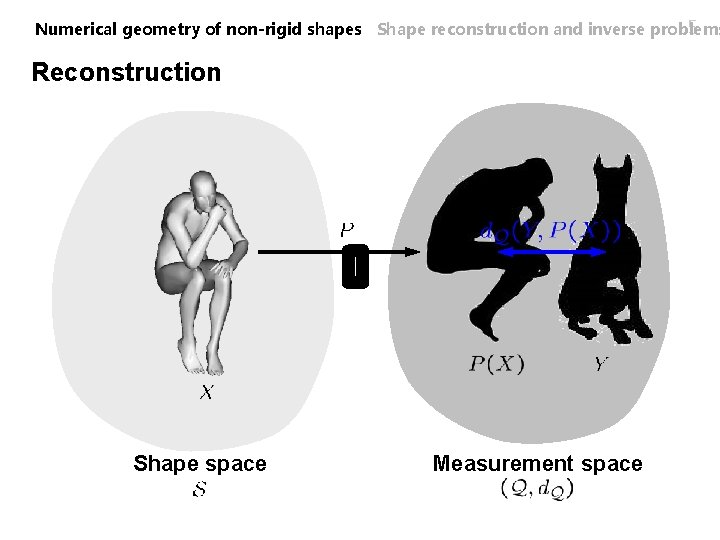
4 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Reconstruction ? Find Shape space Given Measurement space

5 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Reconstruction Shape space Measurement space

6 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Inverse problems Given a (possibly noisy) measurement of unknown shape Reconstruct the shape by minimizing the distance between given measurement and measurement obtained from shape

7 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Inverse problems

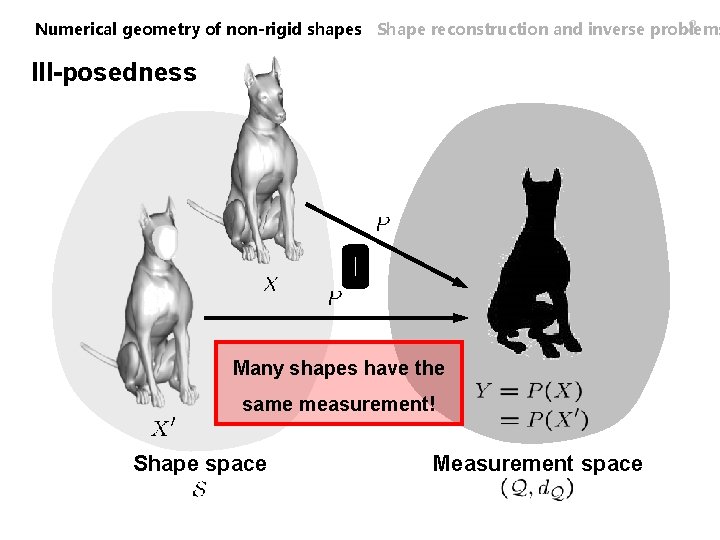
8 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Ill-posedness Many shapes have the same measurement! Shape space Measurement space

9 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Prior knowledge We know that the measurements come from deformations of the same object!

10 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Regularization Deformations of the dog shape Shape space Measurement space

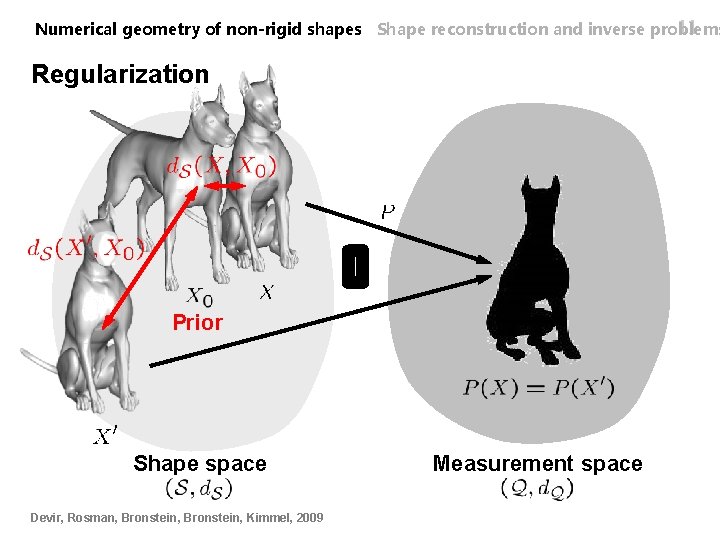
11 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Regularization Prior Shape space Devir, Rosman, Bronstein, Kimmel, 2009 Measurement space

12 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Inverse problems with intrinsic prior Error Regularization n Prior is given on the intrinsic geometry of the shape (intrinsic prior) n Error = distance between measurements n Regularization = intrinsic distance from prior shape n Prior shape is a deformation of the shape we need to reconstruct Devir, Rosman, Bronstein, Kimmel, 2009

13 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Solution of inverse problems with intrinsic prior n Optimization variable: shape , represented as a set of coordinates n Possible initialization: prior shape n Gradients of and Does it sound familiar? Devir, Rosman, Bronstein, Kimmel, 2009 w. r. t. are required

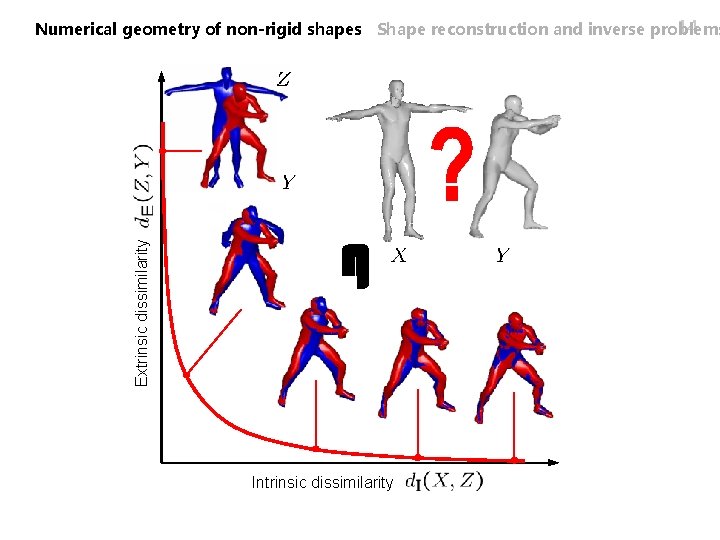
Extrinsic dissimilarity 14 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Intrinsic dissimilarity

15 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Joint similarity as inverse problem n Measurement space = shape space n Identity projection operator n = intrinsic distance on shape space n = extrinsic distance on measurement space n Prior = the shape itself

16 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Computation of the regularization term n Assume shape = deformation of prior with the same connectivity n Trivial correspondence n Compute L 2 distortion of geodesic distances and gradient n n is a fixed (precomputed) matrix of geodesic distances on depends on the variables (must be updated on every iteration) A. Bronstein, M. Bronstein, R. Kimmel, ICCV 2007

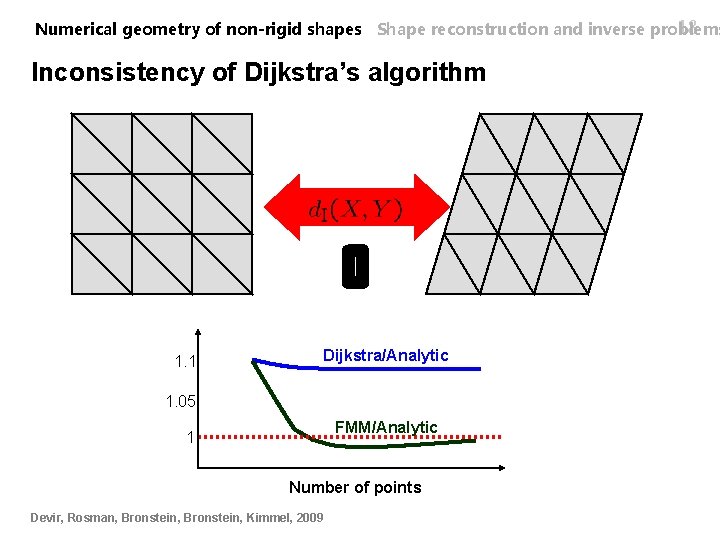
17 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Computation of using Dijkstra’s algorithm n Same approach as in joint similarity n Compute and fix the path of the geodesic n n is a matrix of Euclidean distances between adjacent vertices is a linear operator integrating the path length along fixed path n At each iteration, only n Computation of A. Bronstein, M. Bronstein, R. Kimmel, ICCV 2007 changes is straightforward

18 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Inconsistency of Dijkstra’s algorithm 1. 1 Dijkstra/Analytic 1. 05 FMM/Analytic 1 Number of points Devir, Rosman, Bronstein, Kimmel, 2009

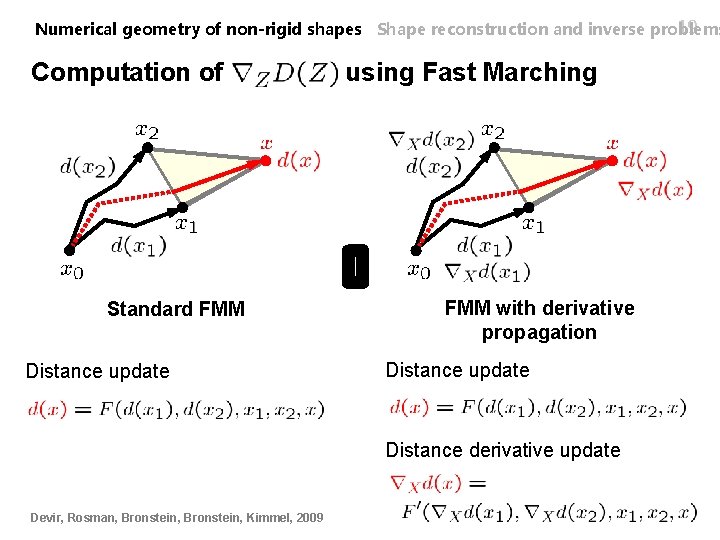
19 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Computation of Standard FMM Distance update using Fast Marching FMM with derivative propagation Distance update Distance derivative update Devir, Rosman, Bronstein, Kimmel, 2009

20 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Shape-from-X Silhouette Shading Image Sparse points Stereo

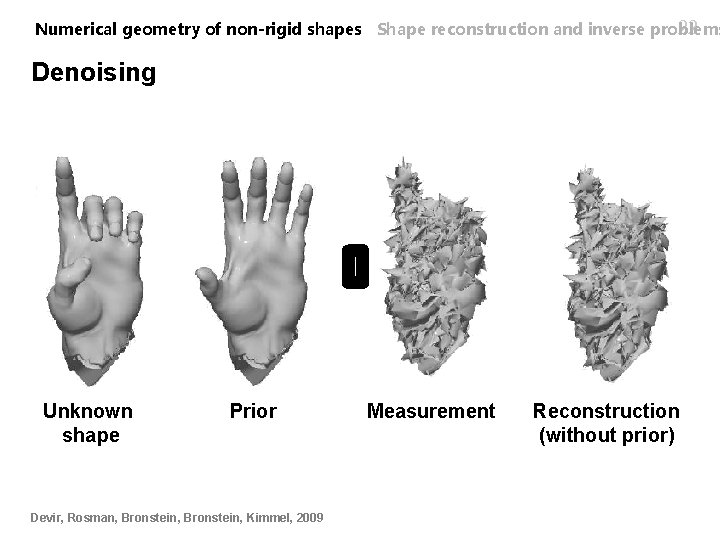
21 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Denoising n Measurement space = shape space n Identity projection operator n = intrinsic distance on shape space n = extrinsic distance on measurement space n Noisy measurement

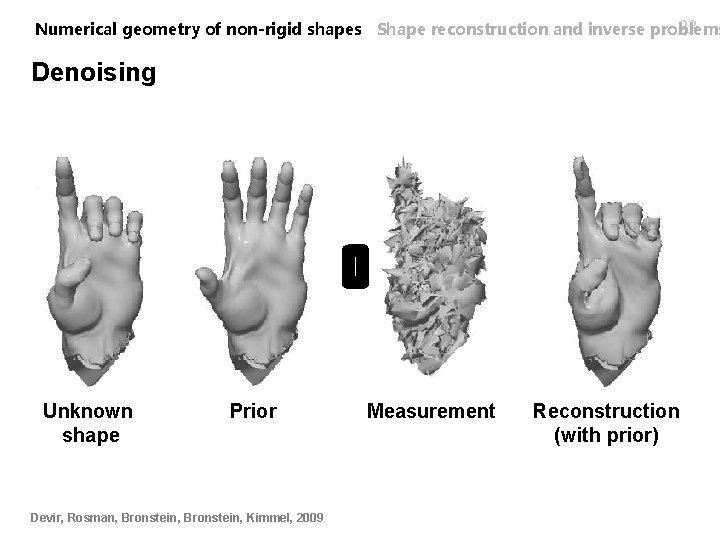
22 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Denoising Unknown shape Prior Devir, Rosman, Bronstein, Kimmel, 2009 Measurement Reconstruction (without prior)

23 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Denoising Unknown shape Prior Devir, Rosman, Bronstein, Kimmel, 2009 Measurement Reconstruction (with prior)

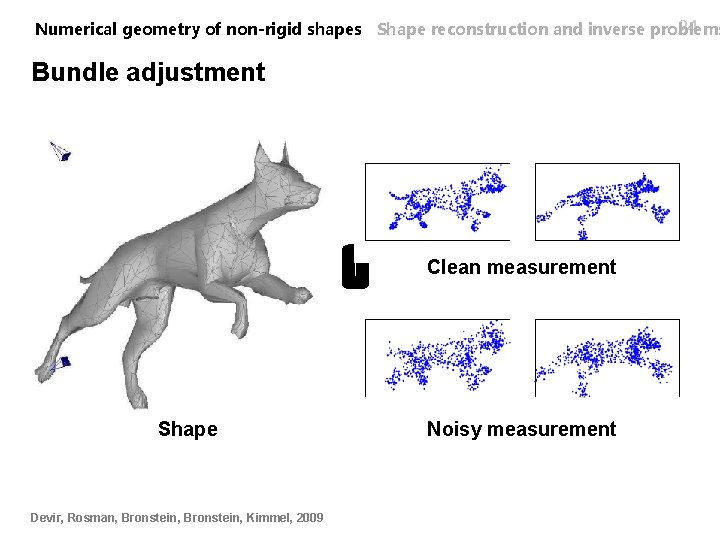
24 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Bundle adjustment Clean measurement Shape Devir, Rosman, Bronstein, Kimmel, 2009 Noisy measurement

25 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Bundle adjustment n Measurement space of 2 D point clouds n Projection operator n (assuming known correspondence) n Noisy measurement

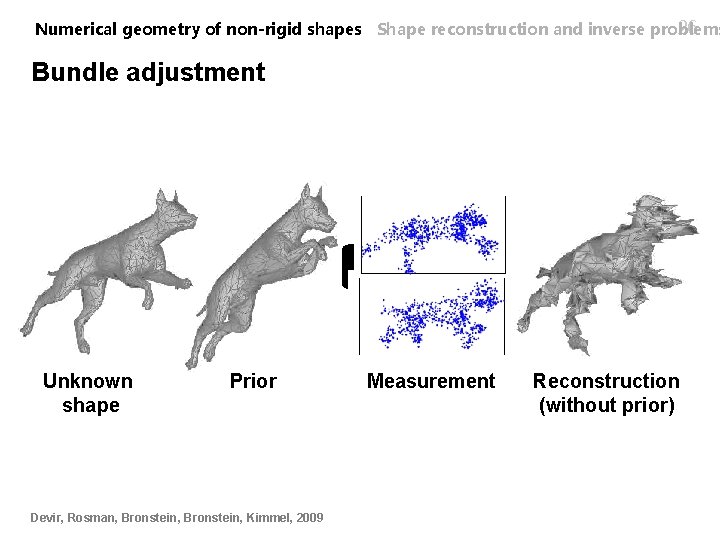
26 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Bundle adjustment Unknown shape Prior Devir, Rosman, Bronstein, Kimmel, 2009 Measurement Reconstruction (without prior)

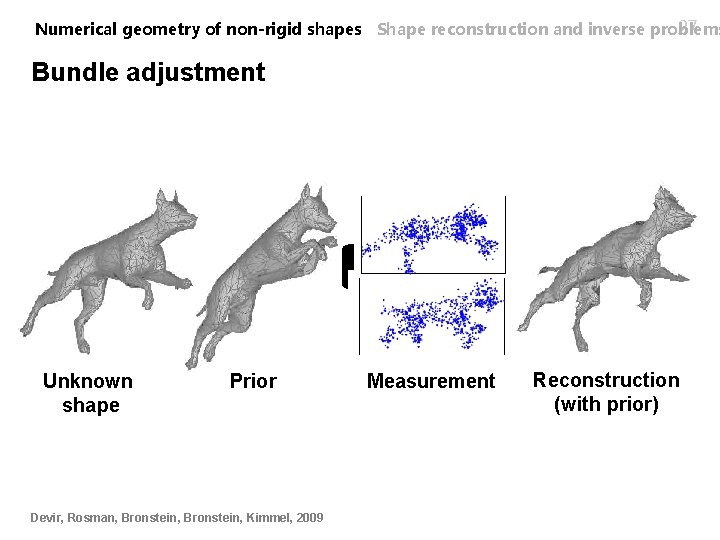
27 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Bundle adjustment Unknown shape Prior Devir, Rosman, Bronstein, Kimmel, 2009 Measurement Reconstruction (with prior)

28 Numerical geometry of non-rigid shapes Shape reconstruction and inverse problems Shape-to-image matching Measured image Salzmann, Pilet, Ilic, Fua, 2007 Reconstruction