1 Logic Circuits Boolean Algebra and Logic Gates

1

ﻣﺪﺍﺭ ﻣﻨﻄﻘی Logic Circuits Boolean Algebra and Logic Gates 2

Algebras �What is an algebra? �Mathematical system consisting of � Set of elements � Set of operators � Axioms or postulates �Why is it important? �Defines rules of “calculations” �Note: operators with two inputs are called binary(e. g. +, -) �Does not mean they are restricted to binary numbers! �Operator(s) with one input are called unary(e. g. √) 3

George Boole �Father of Boolean algebra � He came up with a type of linguistic algebra, the three most basic operations of which were (and still are) AND, OR and NOT. It was these three functions that formed the basis of his premise, and were the only operations necessary to perform comparisons or basic mathematical functions. � Boole’s system (detailed in his 'An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities', 1854) was based on a binary approach, processing only two objects - the yes-no, true-false, on-off, zero-one approach. George Boole (1815 - 1864) � Surprisingly, given his standing in the academic community, Boole's idea was either criticized or completely ignored by the majority of his peers. � Eventually, one bright student, Claude Shannon (19162001), picked up the idea and ran with it 4

Huntington postulates for Boolean algebra �Boolean algebra is an algebraic structure defined by a set of elements, B, together with two binary operators, + and. , provided that: � 1. Closure � 2. Identity element � 3. Commulitative � 4. distributive � 5. complement � 6. There exist at least two element such as B = {0, 1} 5

Venn Diagrams for Postulates X′Y XY X XY′ X′ B 6

Venn Diagrams for Postulates X Y B Set is shaded Y Set X X. Y X+Y isisshaded 7

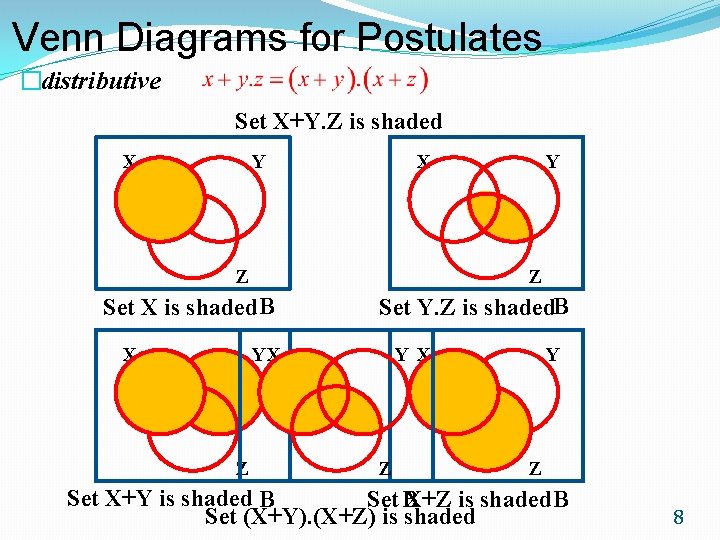
Venn Diagrams for Postulates �distributive Set X+Y. Z is shaded X Y X Z Z Set X is shaded. B X Set Y. Z is shaded. B YX Z Y Z Set X+Y is shaded B Set B X+Z is shaded. B Set (X+Y). (X+Z) is shaded 8

Venn Diagrams for Postulates X. X′ X + X′ Null Set 0 Set X B B Universal Set 1 B Set X′ B 9

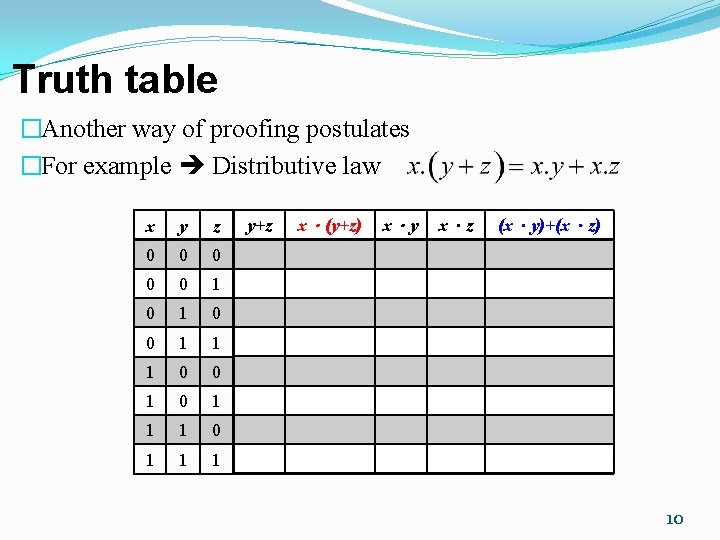
Truth table �Another way of proofing postulates �For example Distributive law x y z y+z x．(y+z) x．y x．z (x．y)+(x．z) 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 0 0 1 1 1 0 1 1 1 1 10

Duality Principle �If an expression is valid in Boolean algebra, the dual of that expression is also valid. �To form a dual of an expression �Replace all + with. �Replace all. with + �Replace all 1 with 0 �Replace all 0 with 1 �Example: a + (b. c) = (a + b). (a + c) a. (b + c) = ab + ac �Take care not to alter the location of the parentheses if they are present. 11

Boolean Theorems �Huntington’s postulates define some rules Post. �Need more rules to modify algebraic expressions 1: 2: 3: 4: closure (a) x+0=x, (b) x· 1=x (a) x+y=y+x, (b) x·y=y·x (a) x(y+z) = xy+xz, (b) x+yz = (x+y)(x+z) Post. 5: (a) x+x’=1, (b) x·x’=0 �Theorems that are derived from postulates �What is a theorem? �A formula or statement that is derived from postulates (or other proven theorems) �Basic theorems of Boolean algebra �Theorem 1 (a): x + x = x (b): x · x = x �Looks straightforward, but needs to be proven ! 12

Basic theorems 13

Proof of x+x=x �We can only use Huntington postulates: �Show that x+x=x. x+x = (x+x)· 1 = (x+x)(x+x’) = x+xx’ = x+0 =x Huntington postulates: Post. 2: (a) x+0=x, (b) x· 1=x Post. 3: (a) x+y=y+x, (b) x·y=y·x Post. 4: (a) x(y+z) = xy+xz, (b) x+yz = (x+y)(x+z) Post. 5: (a) x+x’=1, (b) x·x’=0 by 2(b) by 5(a) by 4(b) by 5(b) by 2(a) �We can now use Theorem 1(a) in future proofs 14

Proof of x·x=x �Similar to previous proof Huntington postulates: Post. 2: (a) x+0=x, (b) x· 1=x Post. 3: (a) x+y=y+x, (b) x·y=y·x Post. 4: (a) x(y+z) = xy+xz, (b) x+yz = (x+y)(x+z) Post. 5: (a) x+x’=1, (b) x·x’=0 Th. 1: (a) x+x=x �Show that x·x = xx+0 = xx+xx’ = x(x+x’) = x· 1 =x by 2(a) by 5(b) by 4(a) by 5(a) by 2(b) �Or we can just use duality principle 15

Proof of x+1=1 �Theorem 2(a): x + 1 = 1．(x + 1) by =(x + x')(x + 1) = x + x' 1 = x + x' =1 �Theorem 2(b): x．0 = 0 Huntington postulates: 2(b) 5(a) 4(b) 2(b) 5(a) Post. 2: (a) x+0=x, (b) x· 1=x Post. 3: (a) x+y=y+x, (b) x·y=y·x Post. 4: (a) x(y+z) = xy+xz, (b) x+yz = (x+y)(x+z) Post. 5: (a) x+x’=1, (b) x·x’=0 Th. 1: (a) x+x=x by duality 16

Absorption Property (Covering) Huntington postulates: �Theorem 6(a): x + xy = x � x + xy = x．1 + xy = x (1 + y) = x (y + 1) = x．1 =x Post. 2: (a) x+0=x, (b) x· 1=x Post. 3: (a) x+y=y+x, (b) x·y=y·x Post. 4: (a) x(y+z) = xy+xz, (b) x+yz = (x+y)(x+z) Post. 5: (a) x+x’=1, (b) x·x’=0 Th. 1: (a) x+x=x by 2(b) 4(a) 3(a) Th 2(a) 2(b) • Theorem 6(b): x (x + y) = x by duality • By means of truth table(another way of proof) x y xy x+xy 0 0 0 1 1 17

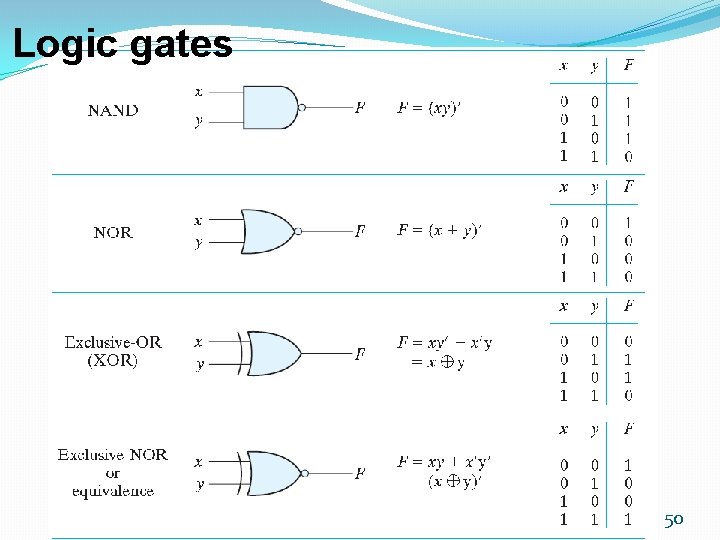
De. Morgan’s Theorem �Theorem 5(a) : �Theorem 5(b) : (x + y)′ = x′y′ (xy)′ = x′ + y′ NAND gate NOR gate �By means of truth table x y x′ y′ x+y (x+y)′ x′y′ xy x′+y′ (xy)′ 0 0 1 1 0 1 0 0 0 1 1 0 0 1 0 0 �(x 1 x 2 x 3 x 4…. )′ = x 1′+x 2′+x 3′+x 4′+…. �(x 1+x 2+x 3+x 4+…)′ = x 1′x 2′x 3′x 4′…. 18

Consensus Theorem 1. 2. xy + x’z + yz = xy + x’z (x+y) • (x’+z) • (y+z) = (x+y) • (x’+z) -- (dual) � Proof: xy + x’z + yz = xy + x’z + (x+x’)yz = xy + x’z + xyz + x’yz = (xy + xyz) + (x’z + x’zy) = xy + x’z 19

Operator Precedence �The operator precedence for evaluating Boolean Expression is �Parentheses �NOT �AND �OR �Examples �x y' + z �(x y + z)' 20

De. Morgan’s Theorem �The rule of complementing an expression: �Replacing each + with. �Replacing each. With + �Replacing each variable by its complement �In applying De. Morgan’s theorem operator precedence must be observed �Example: �(x+yz)′ = ? � x′. (yz) ′ = x′. (y′+z′) = x′y′ + x′z′ � Wrong x′y′+z′ 21

Boolean Functions �A Boolean function �Binary variables �Binary operators OR and AND �Unary operator NOT �Parentheses �Examples �F 1= x y z' �F 2 = x + y'z �F 3 = x' y' z + x' y z + x y' �F 4 = x y' + x' z 22

Boolean Functions �A boolean function F 1 can be uniquely represented by its truth table. �There is only one way that a Boolean function can be represented in a truth table. �However, when the function is in algebraic form, it can be expressed in a variety of ways, �Simplification is needed 23

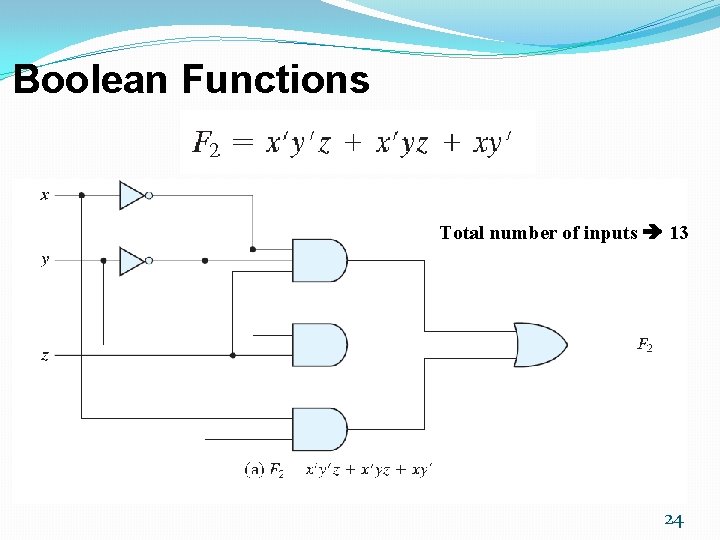
Boolean Functions Total number of inputs 13 24

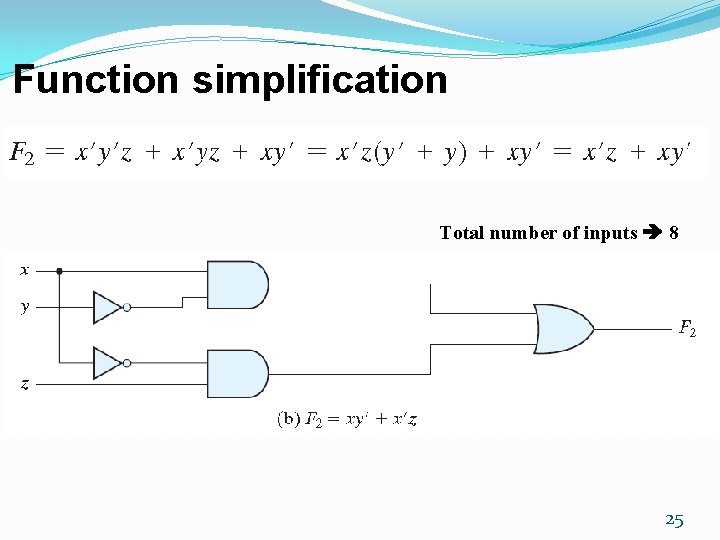
Function simplification Total number of inputs 8 25

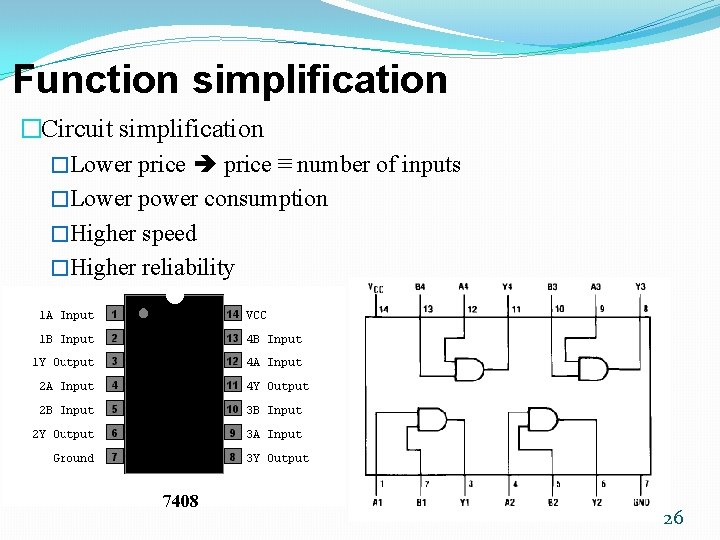
Function simplification �Circuit simplification �Lower price ≡ number of inputs �Lower power consumption �Higher speed �Higher reliability 7408 26

Algebraic Manipulation �By minimizing Boolean expression it is possible to simplify circuit implementation �It is a hard problem (no specific rules to follow) �Algebraic Manipulation �Map simplification �CAD (Computer-Aided Design) �Example: 27

Complementing a function � 1 - De. Morgan’s theorem � 2 - Take the dual of the function and then complement each literal �Example De. Morgan’s theorem Duality 28

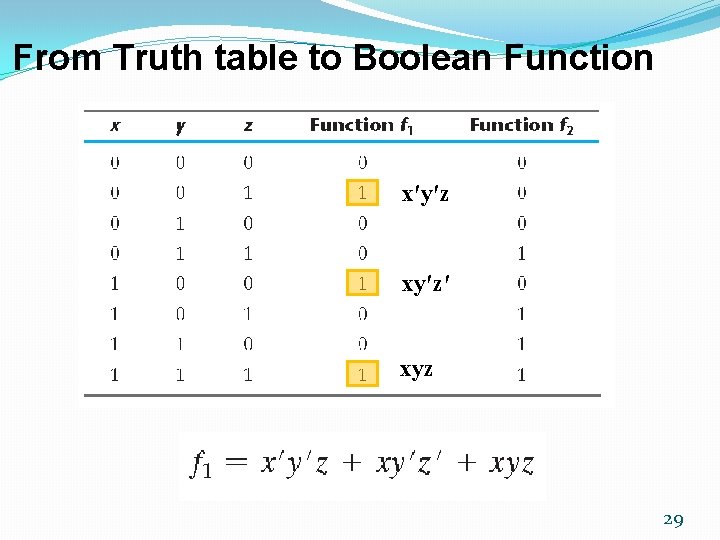
From Truth table to Boolean Function x′y′z xy′z′ xyz 29

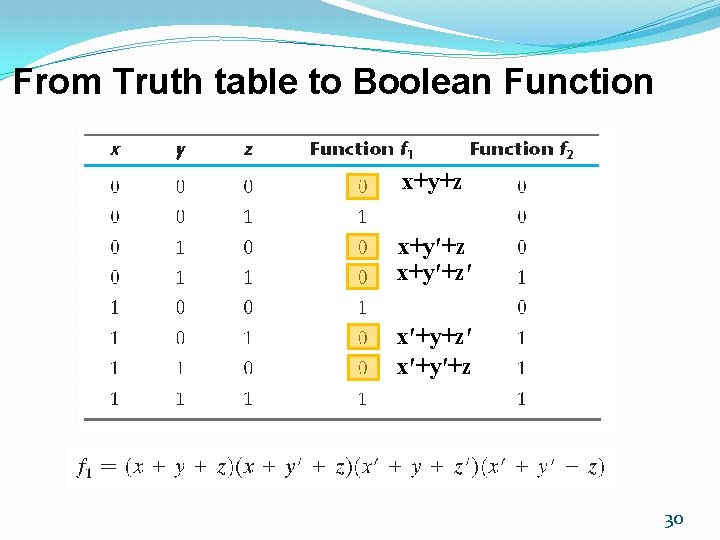
From Truth table to Boolean Function x+y+z x+y′+z′ x′+y′+z 30

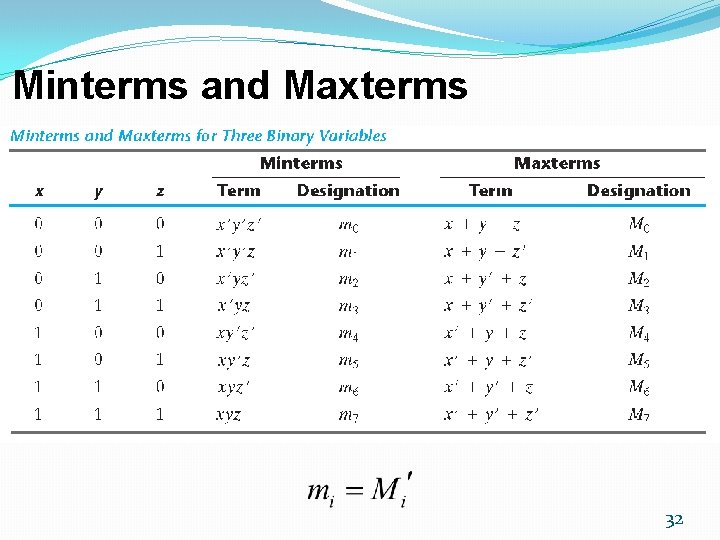
Minterms and Maxterms �A minterm (standard product): an AND term consists of all input literals in their normal form or in their complement form. �A maxterm (standard sums): an OR term consists of all input literals in their normal form or in their complement form. �n literal 2 n Maxterm and 2 n Minterm 31

Minterms and Maxterms 32

From Truth table to Boolean Function �Forming a minterm for each combination of the variables that produces a 1 in the function and then taking the OR of all those terms. (SOM)(Sum Of Minterms) m 1 m 4 m 7 33

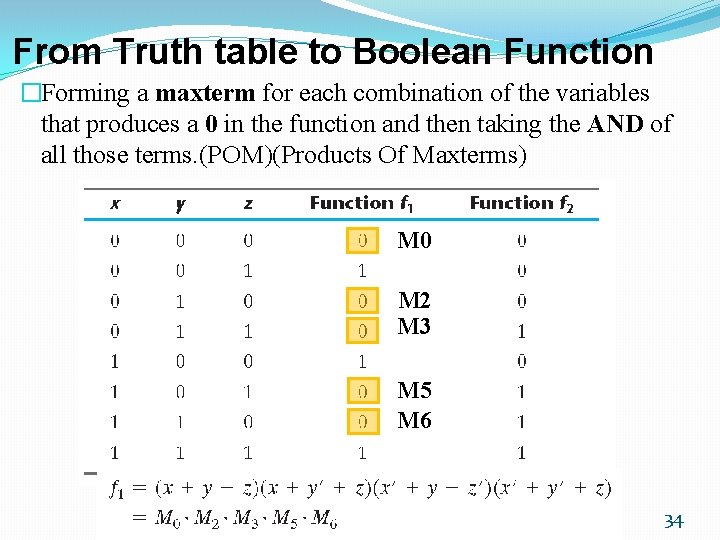
From Truth table to Boolean Function �Forming a maxterm for each combination of the variables that produces a 0 in the function and then taking the AND of all those terms. (POM)(Products Of Maxterms) M 0 M 2 M 3 M 5 M 6 34

Canonical form �Boolean functions expressed as a sum of minterms or product of maxterms are said to be in canonical form. �Two canonical form for each function 35

Converting a function to its canonical form �Express the Boolean function F = A + B′C as a SOM A = A(B + B′) = AB + AB′ A = AB(C + C′) + AB′(C + C′)= ABC + ABC′ + AB′C′ B′C = B′C(A + A′) = AB′C + A′B′C F = A′B′C + AB′C′ + AB′C + ABC′ + ABC m 1 m 4 m 5 m 6 m 7 36

Converting a function to its canonical form �Express the Boolean function F = A + B′C as a SOM 37

Converting a function to its canonical form �Express the Boolean function F = xy + x′z as a POM. �Step 1: using distributive law, x + yz = (x + y)(x + z) bring the function into OR terms. �Step 2: Then any missing variable x in each OR term is ORed with xx′. F = xy + x′z = (xy + x′)(xy + z) = (x + x′)(y + x′)(x + z)(y + z) = (x′ + y)(x + z)(y + z) x′ + y = x′ + y + zz′ = (x′ + y + z)(x′ + y + z′) x + z = x + z + yy′ = (x + y + z)(x + y′ + z) y + z = y + z + xx′ = (x + y + z)(x′ + y + z) F = (x + y + z)(x + y′ + z)(x′ + y + z′) 38

Conversion between canonical forms �The complement of a function expressed as the sum of minterms equals the sum of minterms missing from the original function. �By De. Morgan theorems 39

Standard forms �Canonical forms are very seldom the ones with the least number of literals. �Each minterm or maxterm must contain, by definition, all the variables, either complemented or uncomplemented. �Standard form �The terms that form the function may contain one, two, or any number of literals. �Two standard forms �SOP(Sum Of Products) �POS(Product of Sums) 40

SOP �The sum of products is a Boolean expression containing AND terms, called product terms, with one or more literals each. �The sum denotes the ORing of these terms. 41

POS �A product of sums is a Boolean expression containing OR terms, called sum terms. Each term may have any number of literals. �The product denotes the ANDing of these terms. 42

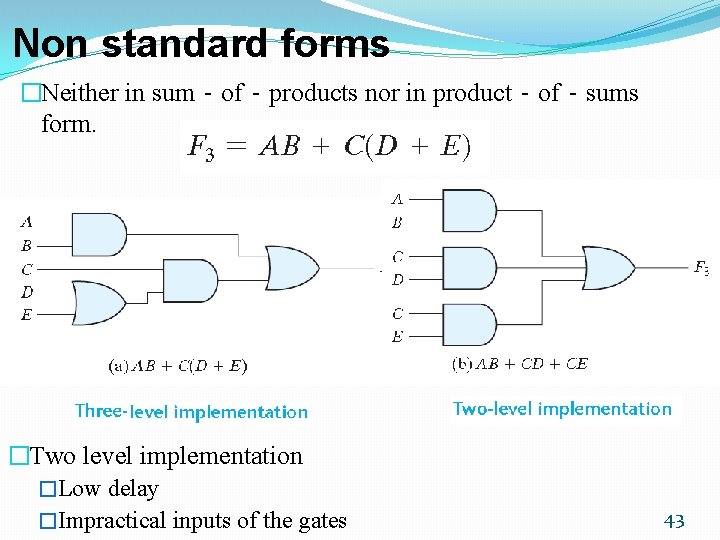
Non standard forms �Neither in sum‐of‐products nor in product‐of‐sums form. �Two level implementation �Low delay �Impractical inputs of the gates 43

Other Logic Operations �How many functions can be constructed by n Boolean variable? �Functions are combination of Minterms or Maxterms. �n variable 2 n minterms or maxterms �Each minterm or maxterm has two binary value 0 or 1 �Two of the functions are constant F = 0, F = 1 �n = 2 16 or 14 �n = 5 4294967296!! �n = 8 1. 1579208923731619542357098500869 e+77 44

Other Logic Operations �The 16 functions listed can be subdivided into three categories: � 1 - Two functions that produce a constant 0 or 1. � 2 - Four functions with unary operations: complement and transfer. � 3 - Ten functions with binary operators that define eight different operations: AND, OR, NAND, NOR, exclusive‐OR, equivalence, inhibition, and implication. 45

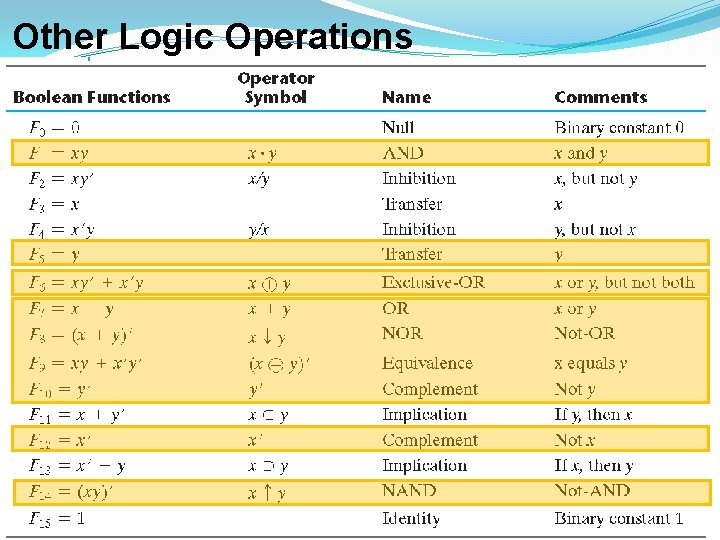
Other Logic Operations 46

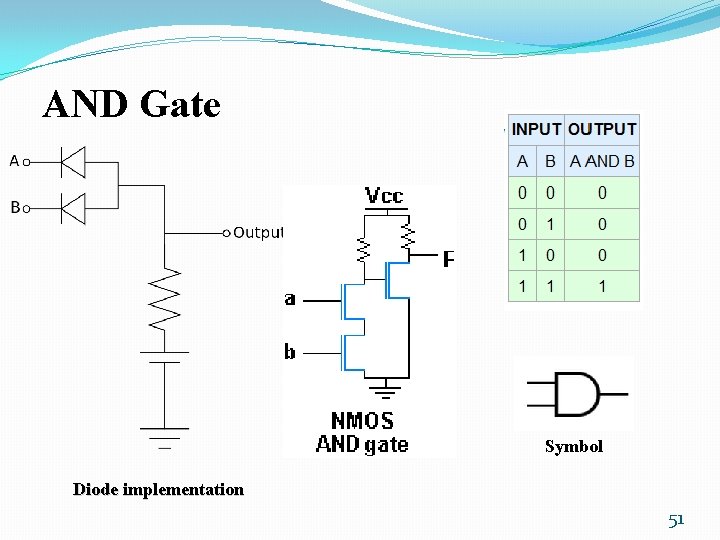
Digital Logic Gates �Boolean expression: AND, OR and NOT operations �Constructing gates of other logic operations �The feasibility and economy; �The possibility of extending gate's inputs; �The basic properties of the binary operations (commutative and associative); �The ability of the gate to implement Boolean functions. 47

Standard Gates �Consider the 16 functions in Table of slide 46 �Two are equal to a constant (F 0 and F 15). �Four are repeated twice (F 4, F 5, F 10 and F 11). �Inhibition (F 2) and implication (F 13) are not commutative or associative. �The other eight: complement (F 12), transfer (F 3), AND (F 1), OR (F 7), NAND (F 14), NOR (F 8), XOR (F 6), and equivalence (XNOR) (F 9) are used as standard gates. �Complement: inverter. �Transfer: buffer (increasing drive strength). �Equivalence: XNOR. 48

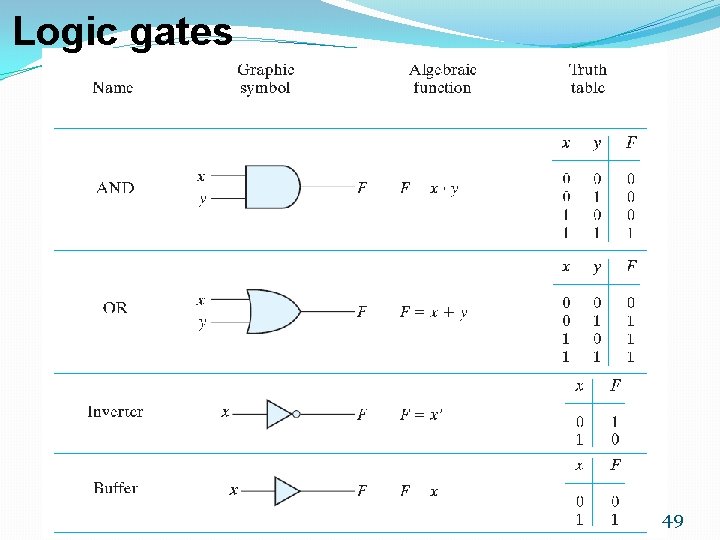
Logic gates 49

Logic gates 50

AND Gate Symbol Diode implementation 51

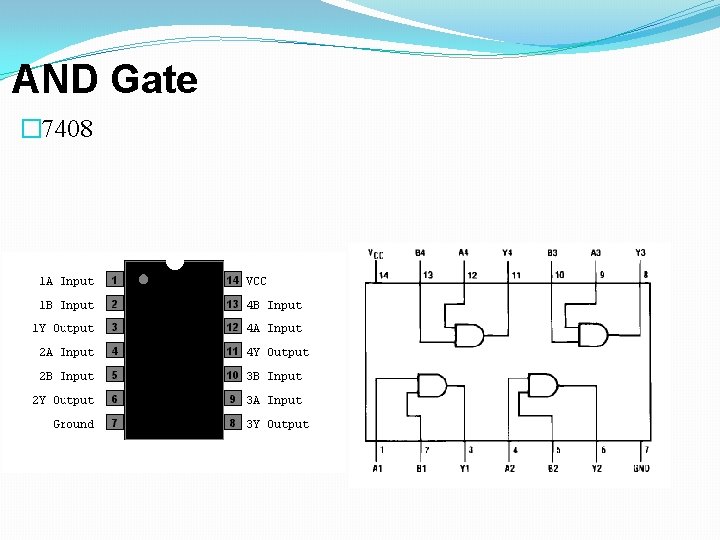
AND Gate � 7408

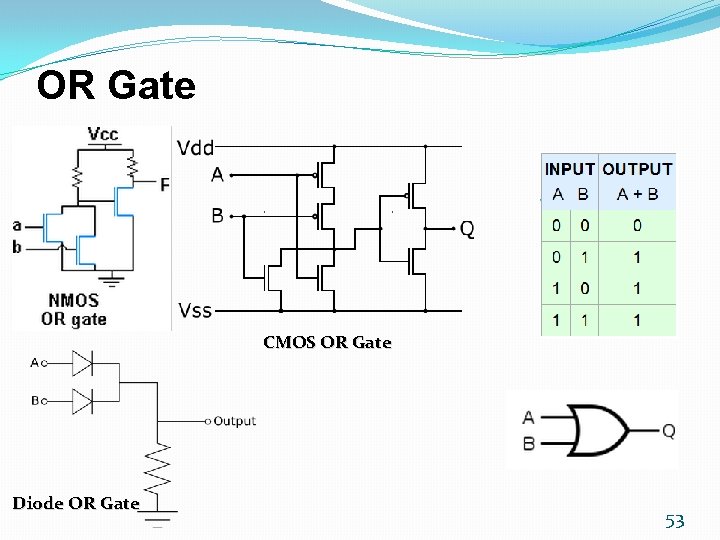
OR Gate CMOS OR Gate Diode OR Gate 53

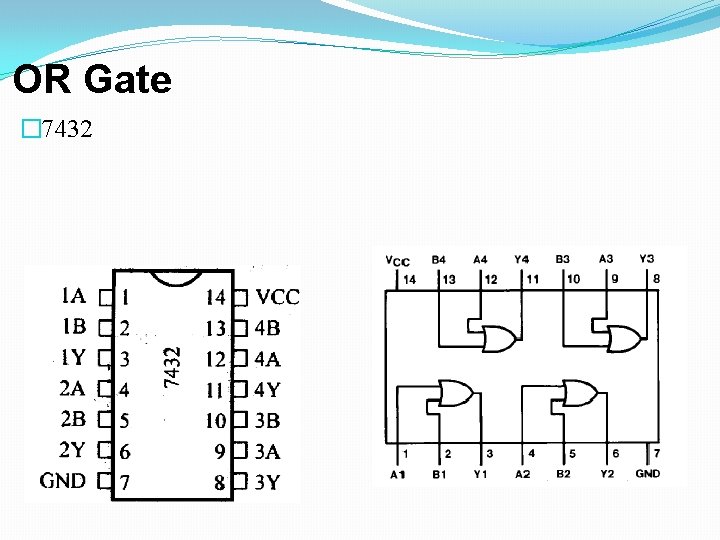
OR Gate � 7432

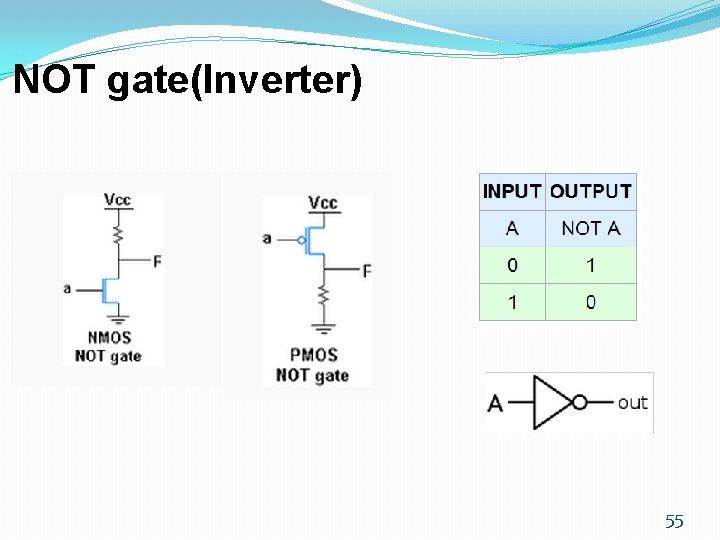
NOT gate(Inverter) 55

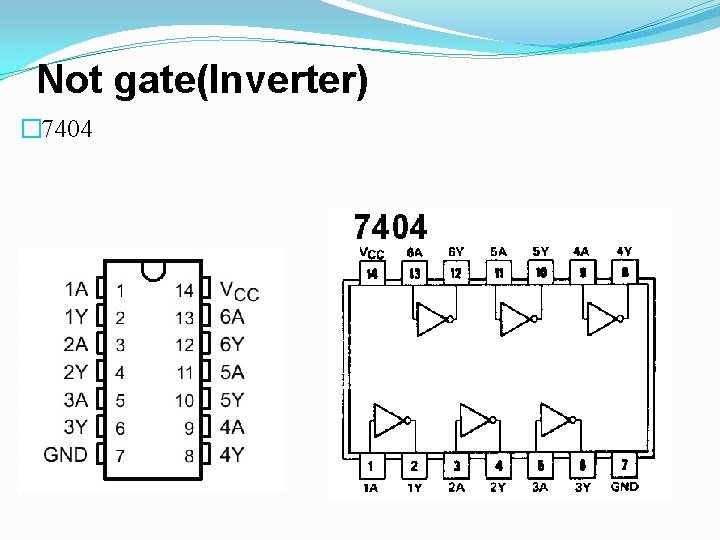
Not gate(Inverter) � 7404

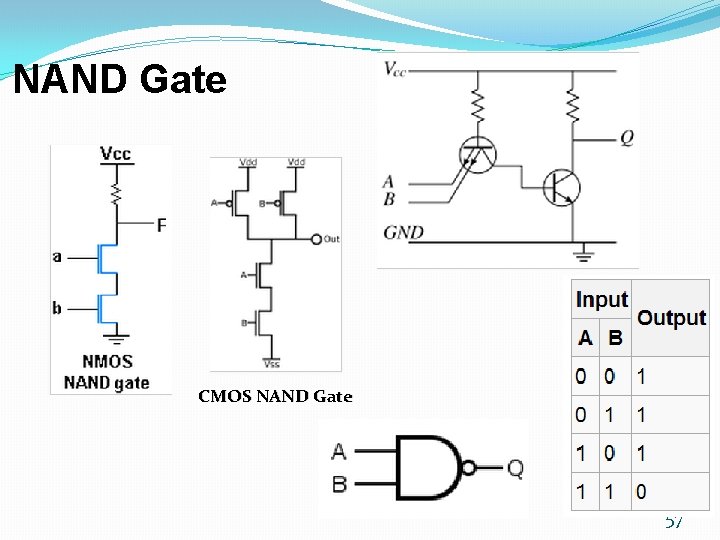
NAND Gate CMOS NAND Gate 57

NAND Gate � 7400

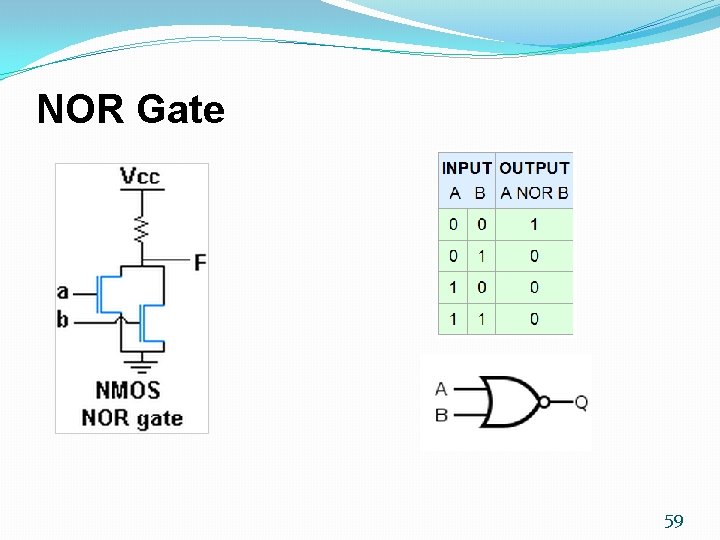
NOR Gate 59

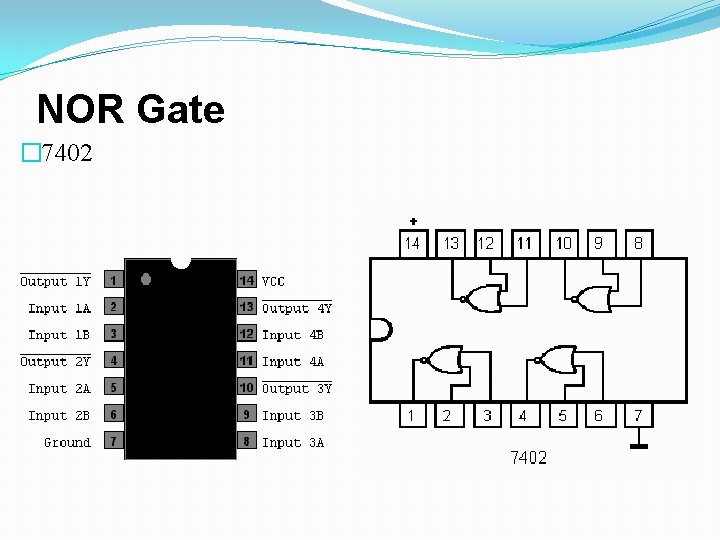
NOR Gate � 7402

Extension Multiple Inputs �Extension to multiple inputs �A gate can be extended to multiple inputs. � If its binary operation is commutative and associative. �AND and OR are commutative and associative. � OR �x+y = y+x �(x+y)+z = x+(y+z) = x+y+z � AND �xy = yx �(x y)z = x(y z) = x y z 61

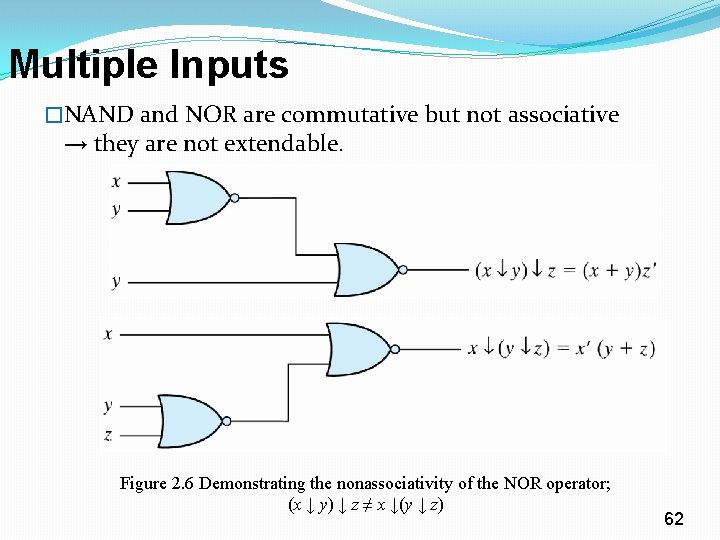
Multiple Inputs �NAND and NOR are commutative but not associative → they are not extendable. Figure 2. 6 Demonstrating the nonassociativity of the NOR operator; (x ↓ y) ↓ z ≠ x ↓(y ↓ z) 62

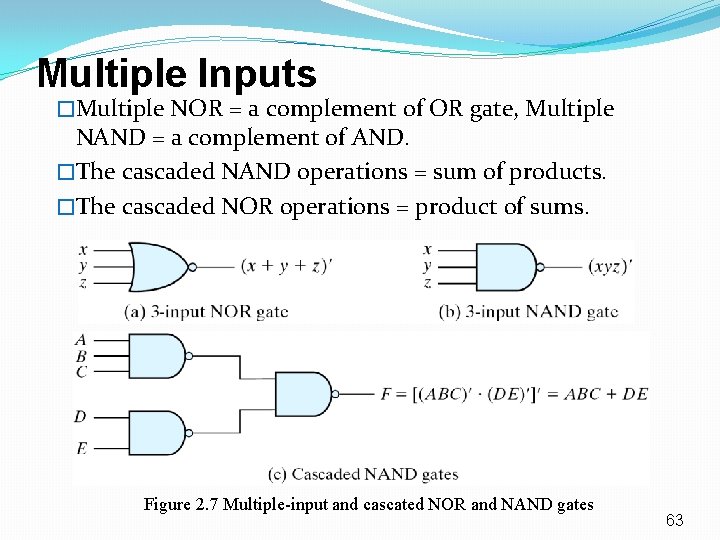
Multiple Inputs �Multiple NOR = a complement of OR gate, Multiple NAND = a complement of AND. �The cascaded NAND operations = sum of products. �The cascaded NOR operations = product of sums. Figure 2. 7 Multiple-input and cascated NOR and NAND gates 63

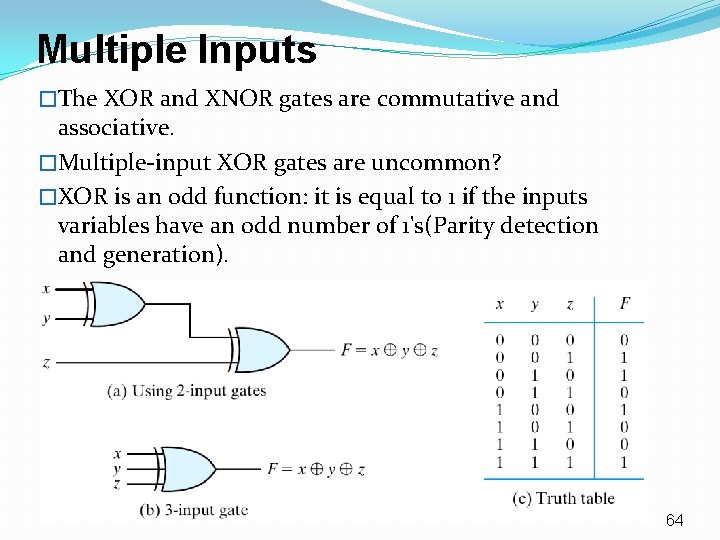
Multiple Inputs �The XOR and XNOR gates are commutative and associative. �Multiple-input XOR gates are uncommon? �XOR is an odd function: it is equal to 1 if the inputs variables have an odd number of 1's(Parity detection and generation). 64

Positive and Negative Logic �Two signal values <=> two logic values �Positive logic: H=1; L=0 �Negative logic: H=0; L=1 �Consider a TTL gate �A positive logic AND gate �A negative logic OR gate �The positive logic is used in this book Figure 2. 9 Signal assignment and logic polarity 65

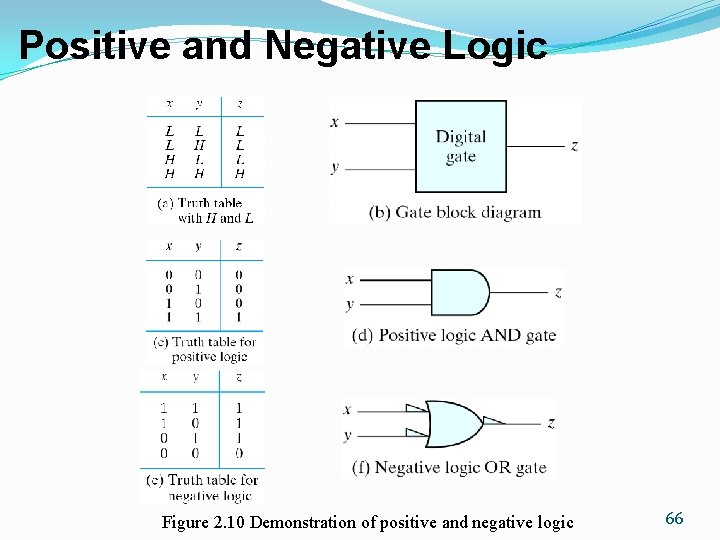
Positive and Negative Logic Figure 2. 10 Demonstration of positive and negative logic 66

Integrated Circuits Level of Integration �An IC (a chip) �Examples: �Small-scale Integration (SSI): < 10 gates �Medium-scale Integration (MSI): 10 ~ 100 gates �Large-scale Integration (LSI): 100 ~ xk gates �Very Large-scale Integration (VLSI): > xk gates, Millions �Ultra Large-scale Integration (ULSI): Billions �VLSI �Small size (compact size) �Low cost �Low power consumption �High reliability �High speed 67

Digital Logic Families �Digital logic families: circuit technology �TTL: transistor-transistor logic (dying? ) �ECL: emitter-coupled logic (high speed, high power consumption) �MOS: metal-oxide semiconductor (NMOS, high density) �CMOS: complementary MOS (low power) �Bi. CMOS: high speed, high density 68

Digital Logic Families �The characteristics of digital logic families �Fan-out: the number of standard loads that the output of a typical gate can drive. �Power dissipation. �Propagation delay: the average transition delay time for the signal to propagate from input to output. �Noise margin: the minimum of external noise voltage that caused an undesirable change in the circuit output. 69

CAD �CAD – Computer-Aided Design �Millions of transistors �Computer-based representation and aid �Automatic the design process �Design entry � Schematic capture � HDL – Hardware Description Language �Verilog, VHDL �Simulation �Physical realization � ASIC, FPGA, PLD 70

Chip Design �Why is it better to have more gates on a single chip? � Easier to build systems � Lower power consumption � Higher clock frequencies �What are the drawbacks of large circuits? � Complex to design � Chips have design constraints � Hard to test �Need tools to help develop integrated circuits � Computer Aided Design (CAD) tools � Automate tedious steps of design process � Hardware description language (HDL) describe circuits � VHDL is one such system 71

Home Works � 2. 8, 2. 9, 2. 10, 2. 12, 2. 13, 2. 17, 2. 18, 2. 20, 2. 21, 2. 23, 2. 27, 2. 28. 2. 29 72