1 Lightningfast simulation of open system an effortless


















- Slides: 28

1 Lightning-fast simulation of open system: an effortless modal approach (GENOME) Dr Parry Y. Chen, Ben Gurion U. Prof. David J. Bergman, Tel Aviv U. Prof. Egor A. Muljarov, Cardiff U. Prof. Yonatan Sivan, Ben Gurion U.

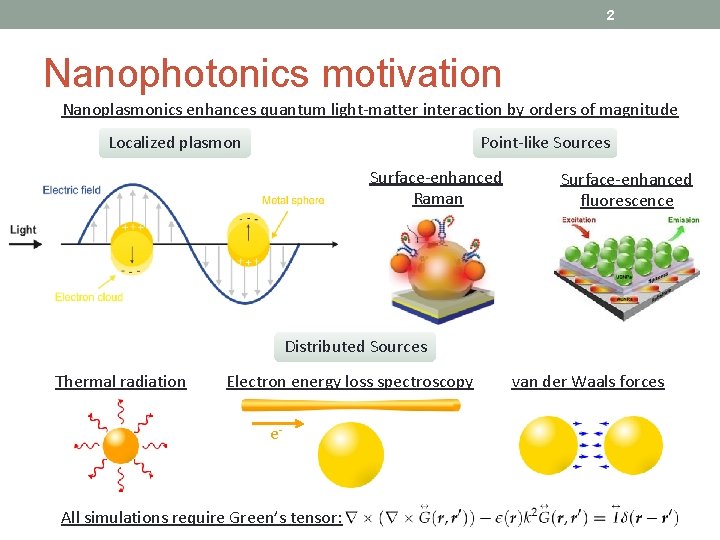
2 Nanophotonics motivation Nanoplasmonics enhances quantum light-matter interaction by orders of magnitude Localized plasmon Point-like Sources Surface-enhanced Raman Surface-enhanced fluorescence Distributed Sources Thermal radiation Electron energy loss spectroscopy e- All simulations require Green’s tensor: van der Waals forces

3 Electrodynamics Simulation Our methods are general to all PDEs, but in this presentation, we consider Maxwell’s Equations • General sources, general structure Green’s Tensor • • r’ If source is a point, defines Green’s tensor Gives electromagnetic density of states Many applications in optics e. g. spontaneous emission rate, Purcell factor, thermal emission, electron-energy loss spectroscopy, dipole-dipole intn’s, … r

4 COMSOL: Direct Solution Overview of FEM • Discretize space • Convert differential equation to linear system of equations • Solve by “matrix inversion” • Repeat simulation for each source distribution Finite Element Mesh

5 COMSOL: Frequency Domain Modal Overview for closed systems First, solve for eigenmode Provides complete basis to expand fields Expand sources using eigenmodes Solution for any source obtained instantaneously! Accurate results using only a few modes: enables physical insight

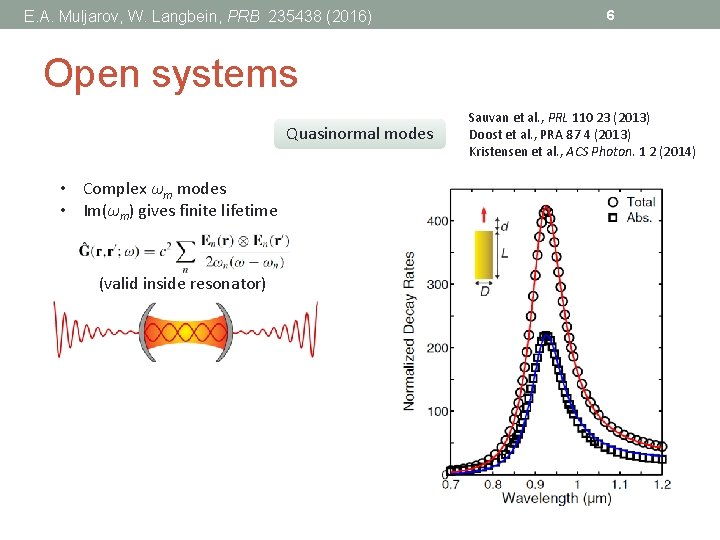
E. A. Muljarov, W. Langbein, PRB 235438 (2016) 6 Open systems Quasinormal modes • Complex ωm modes • Im(ωm) gives finite lifetime (valid inside resonator) Sauvan et al. , PRL 110 23 (2013) Doost et al. , PRA 87 4 (2013) Kristensen et al. , ACS Photon. 1 2 (2014)

7 Open systems Quasinormal modes • Complex ωm modes • Im(ωm) gives finite lifetime Sauvan et al. , PRL 110 23 (2013) Doost et al. , PRA 87 4 (2013) Kristensen et al. , ACS Photon. 1 2 (2014) (valid inside resonator) • Diverges at infinity since k. R and -ωt are opposite in sign • Incomplete basis • Non-linear eigenvalue equation Lalanne et al. , Ar. Xiv 170502433 (2017) Solution correct only inside

P. Y. Chen, D. J Bergman, Y. Sivan, PRApplied 044018 (2019) 8 GENOME (Gen. Normal Mode Exp. ) Our alternative to quasinormal modes Goal: generalize normal mode expansion to open systems Concept Fix frequency and geometry. Resonance condition: eigenpermittivity ϵm r’ ϵb ϵi r ϵm free-space Green’s tensor • • Decays to 0 at infinity Valid over all space Always a discrete set of modes Linear eigenvalue equation detuning from resonance

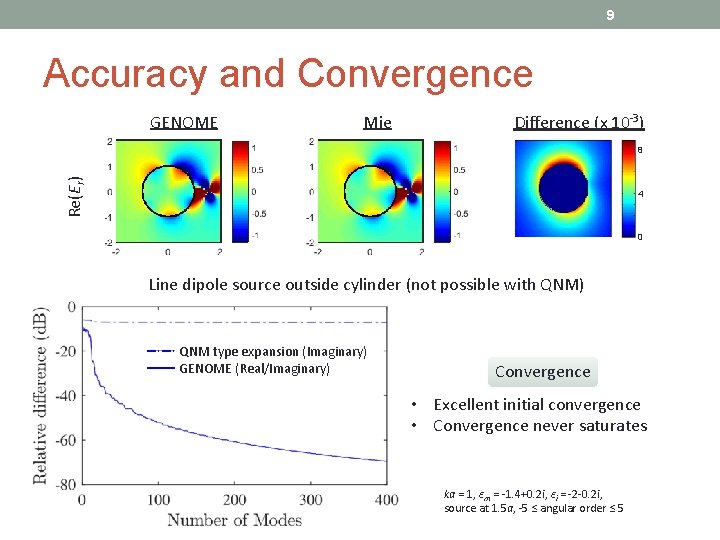
9 Accuracy and Convergence GENOME Mie Difference (x 10 -3) Re(Er) 8 4 0 Line dipole source outside cylinder (not possible with QNM) QNM type expansion (Imaginary) GENOME (Real/Imaginary) Convergence • Excellent initial convergence • Convergence never saturates ka = 1, εm = -1. 4+0. 2 i, εi = -2 -0. 2 i, source at 1. 5 a, -5 ≤ angular order ≤ 5

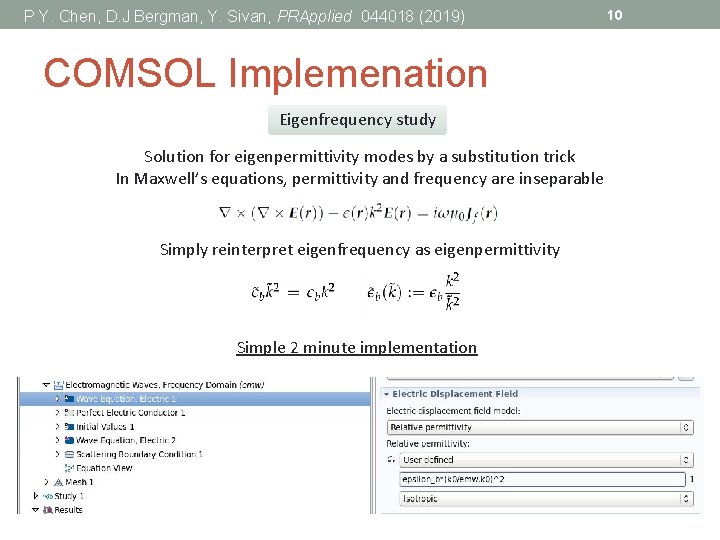
P. Y. Chen, D. J Bergman, Y. Sivan, PRApplied 044018 (2019) COMSOL Implemenation Eigenfrequency study Solution for eigenpermittivity modes by a substitution trick In Maxwell’s equations, permittivity and frequency are inseparable Simply reinterpret eigenfrequency as eigenpermittivity Simple 2 minute implementation 10

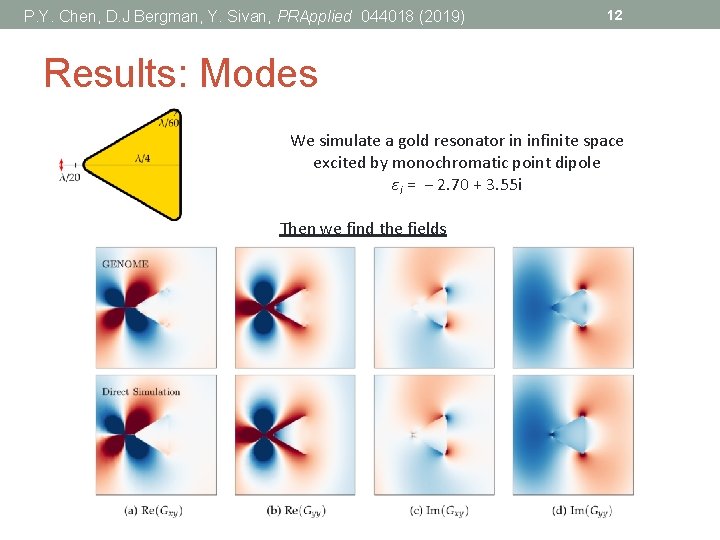
P. Y. Chen, D. J Bergman, Y. Sivan, PRApplied 044018 (2019) 11 Results: Modes We simulate a gold resonator in infinite space excited by monochromatic point dipole εi = − 2. 70 + 3. 55 i First we find the modes

P. Y. Chen, D. J Bergman, Y. Sivan, PRApplied 044018 (2019) 12 Results: Modes We simulate a gold resonator in infinite space excited by monochromatic point dipole εi = − 2. 70 + 3. 55 i Then we find the fields

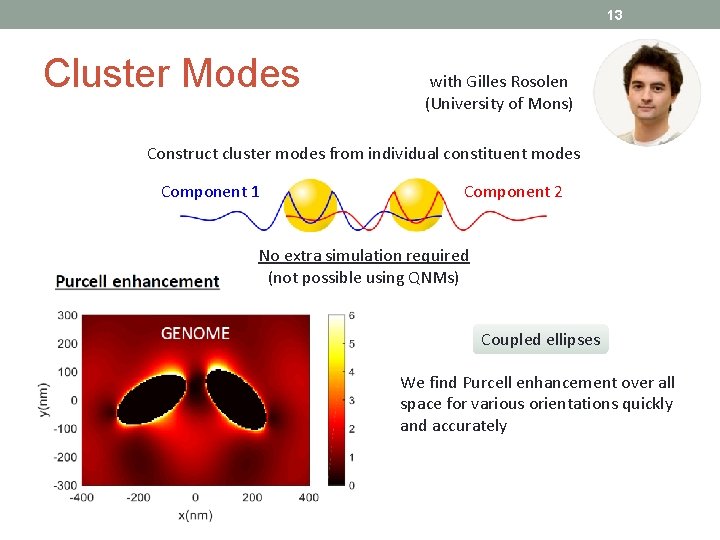
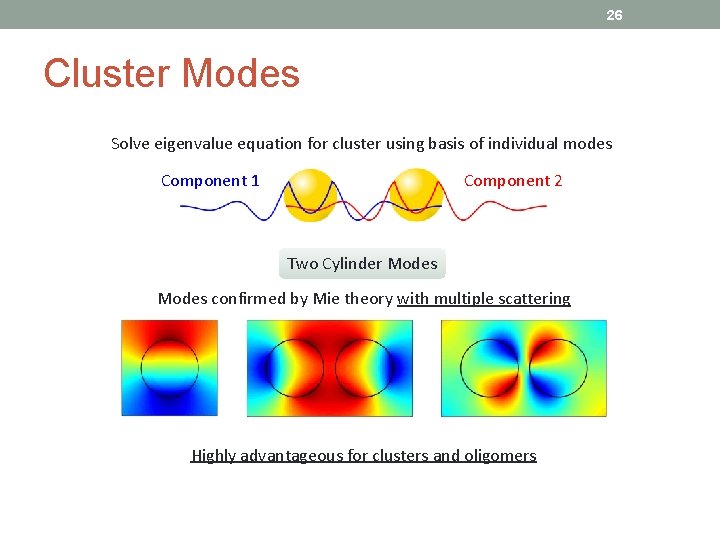
13 Cluster Modes with Gilles Rosolen (University of Mons) Construct cluster modes from individual constituent modes Component 1 Component 2 No extra simulation required (not possible using QNMs) Coupled ellipses We find Purcell enhancement over all space for various orientations quickly and accurately

P. Y. Chen, D. J Bergman, Y. Sivan, PRApplied 044018 (2019) Conclusion Generalized Normal Mode Expansion (GENOME) • GENOME successfully treats open systems via modal expansion • Modes are discrete and complete ϵb r’ r ϵi ϵm Applicable to open systems in… Acoustics and geophysics Quantum Mechanics and other PDEs 14

15 SUPPLEMENTARY SLIDES

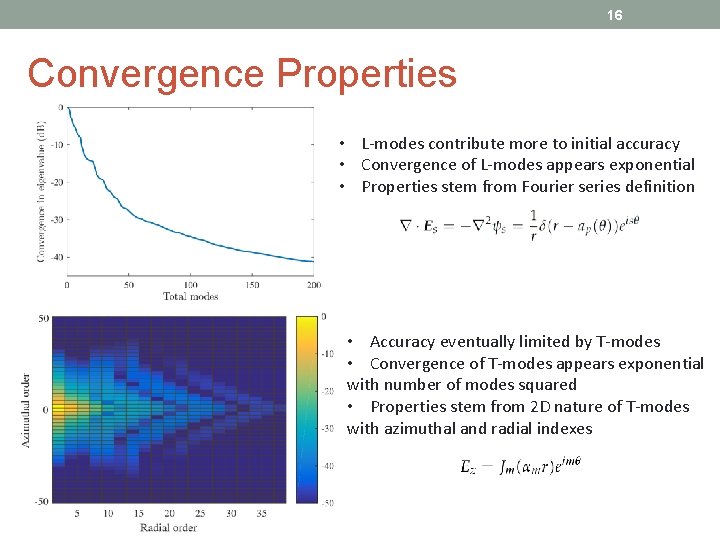
16 Convergence Properties • L-modes contribute more to initial accuracy • Convergence of L-modes appears exponential • Properties stem from Fourier series definition • Accuracy eventually limited by T-modes • Convergence of T-modes appears exponential with number of modes squared • Properties stem from 2 D nature of T-modes with azimuthal and radial indexes

17 Simplified overlap integrals Aim: reduce area integrals to contour integrals Area integral Contour integral Idea: clever use of vector identities Conclusion: we only need the L-mode and its potential along the deformation boundary

18 Intricacies of integration Evaluation of E can be difficult due to singularity at r = r’ Integral can only be defined as Cauchy principal value However, the PV is the average of the two limiting values Eave E(1) E(2) The difference between the limiting values also needs to be calculated The difference is just the Dirac-delta weight

19 Lossy Modal Expansion • Radiation losses • Material losses Normal modes not applicable Loss Quasinormal modes Sauvan et al. , PRL 110 23 (2013) Doost et al. , PRA 87 4 (2013) Kristensen et al. , ACS Photon. 1 2 (2014) • Complex ωm modes • Im(ωm) gives finite lifetime • Diverges at infinity since k. R and -ωt are opposite in sign • Normalization is more difficult • Approximate: incomplete basis • Can require modal continuum • Non-linear eigenvalue equation

20 Completeness? Discrete Set • Each ϵ-eigenmode radiates (Sommerfeld radiation condition) • Infinite but discrete modes Im[ϵm] Why are our modes discrete? Eigenmodes Are our modes complete for the interior? Re[ϵm] Higher order modes approach infinite potential well ϵm - ϵb Conjecture which is known to have a complete set of modes Based on: G. Birkhoff & G Rota, On the completeness of Sturm-Liouville expansions, Am. Math. Monthly 67 835 -841 (1960)

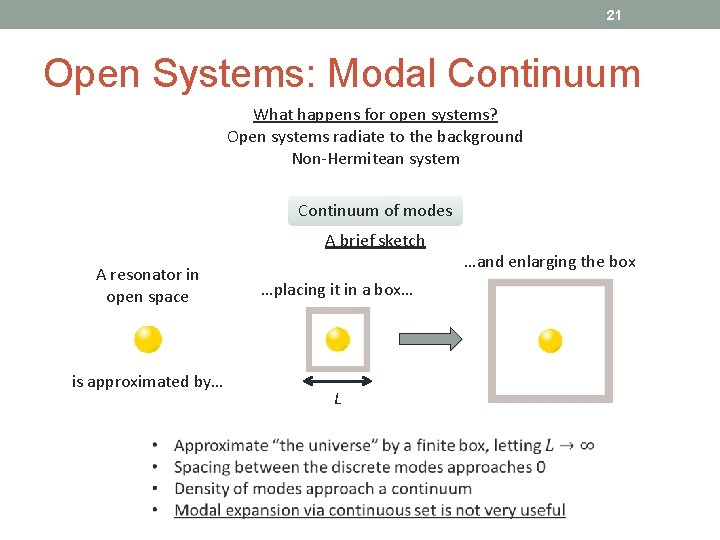
21 Open Systems: Modal Continuum What happens for open systems? Open systems radiate to the background Non-Hermitean system Continuum of modes A brief sketch A resonator in open space is approximated by… …placing it in a box… L …and enlarging the box

22 Simplified overlap integrals Aim: reduce area integrals to contour integrals Area integral Contour integral Idea: clever use of vector identities Example: Ez field Modes satisfy Helmholtz equation Result

23 P. Y. Chen et al. , PRApplied accepted (2018) GENOME Derivation I Begin with Maxwell equations with sources ϵb ϵi Treat structure as another source by moving to RHS Green’s function solution (Lippmann-Schwinger) ϴ(r) = Heaviside function where ϴ(r) = 0 ϴ(r) = 1 Solve using eigenmodes • Permittivity is the eigenvalue • Provides complete basis for fields inside structure • Completeness extends to background fields via Lipp-Schw.

P. Y. Chen et al. , PRApplied accepted (2018) 24 GENOME Derivation II Compact notation: Farhi & Bergman, PRA 93 063844 (2016) Formal solution: ϵb Solve by projecting onto source-free eigenmodes ϵi ϵm NB: ϵm≠ϵi Exploit unified Green’s function to operate on Em, not Jf Solution of Lippmann-Schwinger via projection

25 A Naive Solution First, solve for eigenmodes Assume expansion is possible Insert into Green’s tensor Project and use orthogonality Result is incorrect due to incompleteness! We will demonstrate w/numerics

26 Cluster Modes Solve eigenvalue equation for cluster using basis of individual modes Component 1 Component 2 Two Cylinder Modes confirmed by Mie theory with multiple scattering Highly advantageous for clusters and oligomers

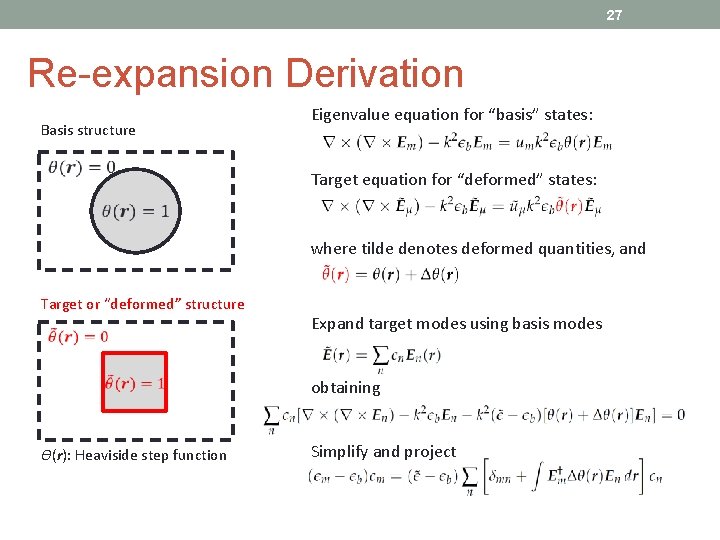
27 Re-expansion Derivation Basis structure Eigenvalue equation for “basis” states: Target equation for “deformed” states: where tilde denotes deformed quantities, and Target or “deformed” structure ϴ(r): Heaviside step function Expand target modes using basis modes obtaining Simplify and project

28 Re-expansion Derivation II Basis structure The linear system of equations Target or “deformed” structure can be put into matrix form, by defining to obtain the matrix ϴ(r): Heaviside step function Matrix is small and dense
 Open innovation open science open to the world
Open innovation open science open to the world Earth is a closed system
Earth is a closed system Explain open and closed system
Explain open and closed system Inventory management simulation pearson
Inventory management simulation pearson Rat cardiovascular system simulation
Rat cardiovascular system simulation On delay timer symbol
On delay timer symbol Open hearts open hands
Open hearts open hands Digestive system circulatory system and respiratory system
Digestive system circulatory system and respiratory system Clam circulatory system
Clam circulatory system Usuf thermodynamics
Usuf thermodynamics Nids open source
Nids open source Contoh open loop system
Contoh open loop system I/o device management in operating system
I/o device management in operating system Arteries and veins difference
Arteries and veins difference Lims software free download
Lims software free download Manakah yang lebih baik open loop atau close loop system
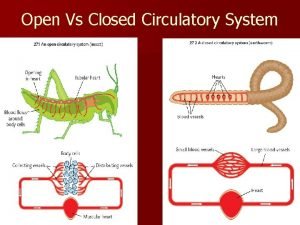
Manakah yang lebih baik open loop atau close loop system Open circulatory system
Open circulatory system Open circulatory system
Open circulatory system Difference between open and closed circulatory system
Difference between open and closed circulatory system Bell coleman air refrigeration cycle
Bell coleman air refrigeration cycle Mass transport in animals
Mass transport in animals Model open system interconnection
Model open system interconnection Partial prefabrication
Partial prefabrication Learning content management system open source
Learning content management system open source Open source it ticketing system
Open source it ticketing system Open system energy balance
Open system energy balance Mollusca open circulatory system
Mollusca open circulatory system Human open system
Human open system Frog circulatory system
Frog circulatory system