1 Isosceles triangles perp bisectors 2 Angle at

1 Isosceles triangles + perp. bisectors 2 Angle at center and at circumference 3 Angle in a semi circle 4 Angles in the same segment 5 Opposite angles in a cyclic quadrilateral 6 Right angle between a tangent and radius 7 Tangential lines the same length 8 Alternate segment theorem

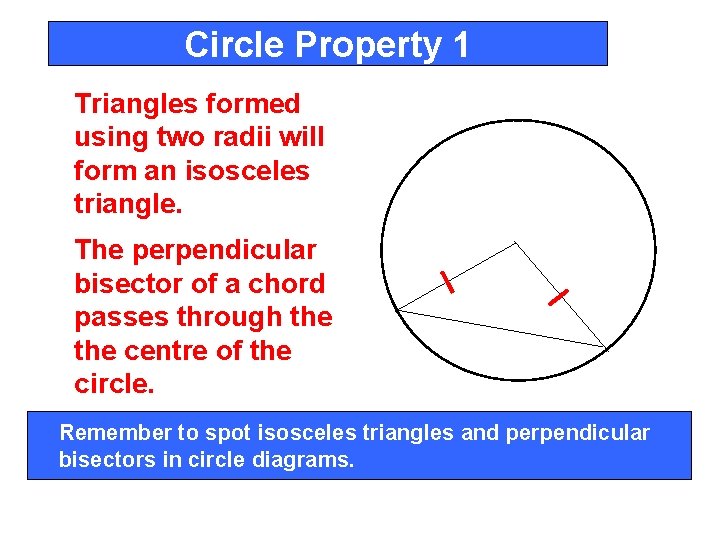
Circle Property 1 Triangles formed using two radii will form an isosceles triangle. The perpendicular bisector of a chord passes through the centre of the circle. Remember to spot isosceles triangles and perpendicular bisectors in circle diagrams.

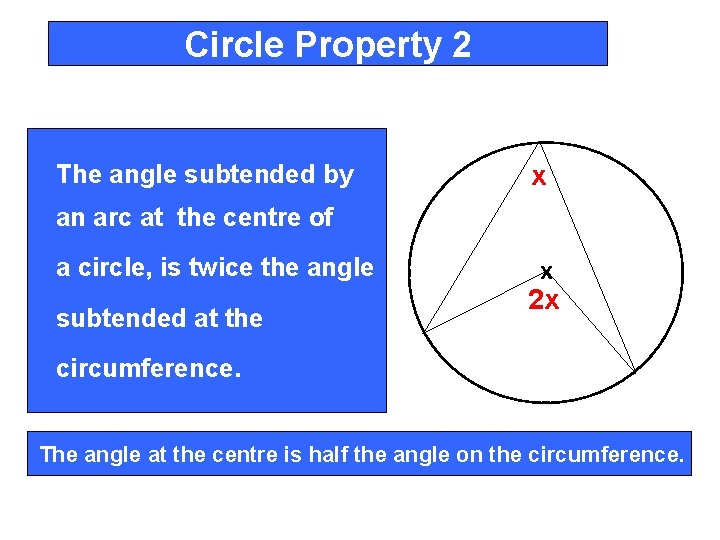
Circle Property 2 The angle subtended by x an arc at the centre of a circle, is twice the angle subtended at the x 2 x circumference. The angle at the centre is half the angle on the circumference.

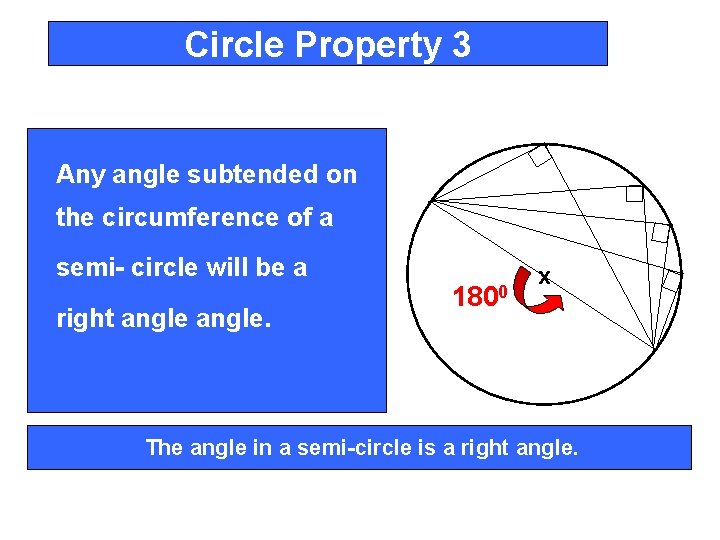
Circle Property 3 Any angle subtended on the circumference of a semi- circle will be a right angle. 1800 x The angle in a semi-circle is a right angle.

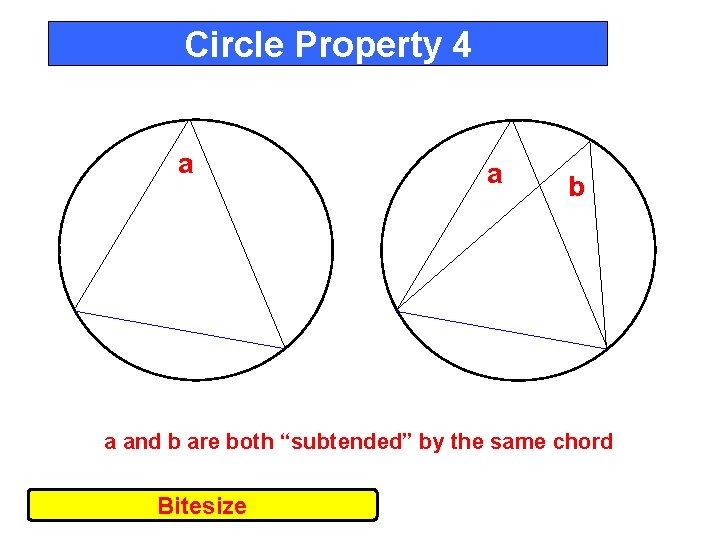
Circle Property 4 a a b a and b are both “subtended” by the same chord Bitesize

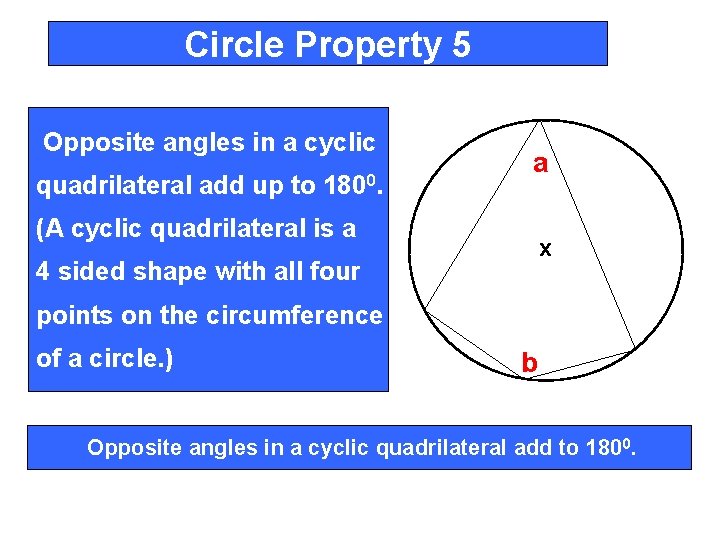
Circle Property 5 Opposite angles in a cyclic quadrilateral add up to 1800. a (A cyclic quadrilateral is a x 4 sided shape with all four points on the circumference of a circle. ) b Opposite angles in a cyclic quadrilateral add to 1800.

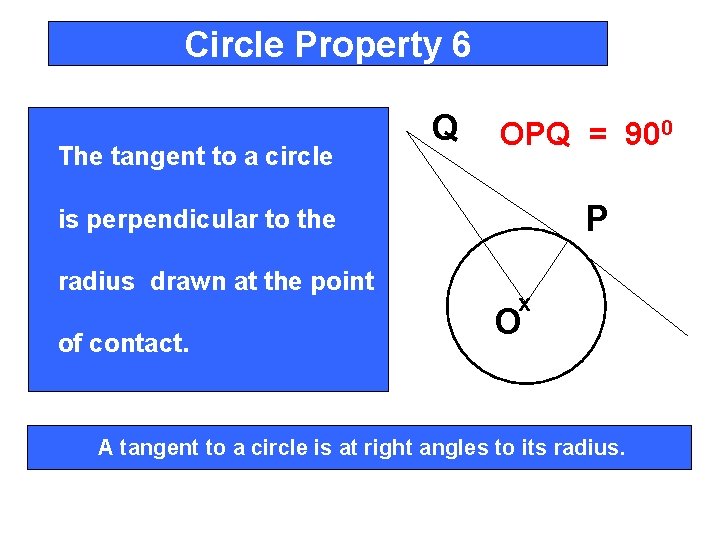
Circle Property 6 The tangent to a circle Q OPQ = 900 P is perpendicular to the radius drawn at the point of contact. x O A tangent to a circle is at right angles to its radius.

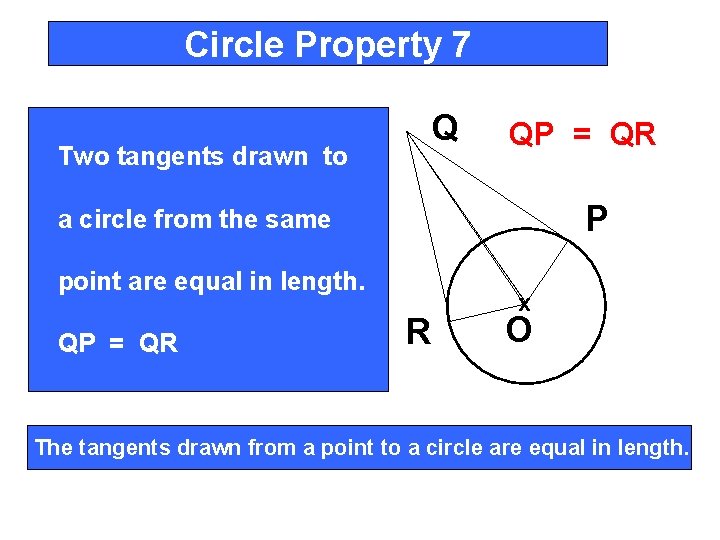
Circle Property 7 Q Two tangents drawn to QP = QR P a circle from the same point are equal in length. QP = QR R x O The tangents drawn from a point to a circle are equal in length.

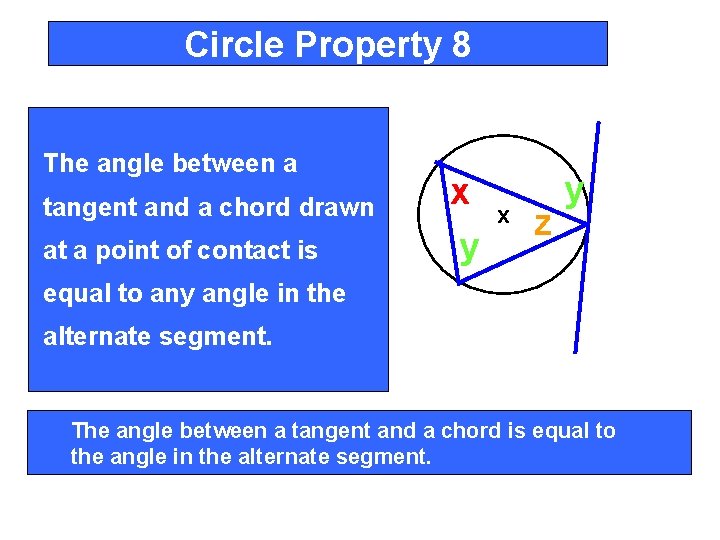
Circle Property 8 The angle between a tangent and a chord drawn at a point of contact is x y x z y equal to any angle in the alternate segment. The angle between a tangent and a chord is equal to the angle in the alternate segment.