1 Introduction to Statistics Elementary Statistics Larson Ch

1 Introduction to Statistics Elementary Statistics Larson Ch 1 Larson/Farber As you view these slides be sure to have paper, pencil, a calculator and your text handy. Click to advance to the slide show. Farber 1

Section 1. 1 An Overview of Statistics After you see the slides for each section, do the Try It Yourself problems in your text for that section to see if you understood the material. Then, do the assigned problems for that section.

Objectives: Ø Define Statistics Ø Distinguish between Population and Sample Ø Distinguish between parameter and Statistics Ø Distinguish between population parameter and sample statistics Ch 1 Larson/Farber 3

What is Statistics? Statistics is the science of collecting, organizing, analyzing, and interpreting data in order to make decisions.

Important Terms • Population The collection of all responses, measurements, or counts that are of interest. • Example: 1. The 5 million South Carolina voters who voted in November's election. 2. Your Turn Ch 1 Larson/Farber 5

Important Terms • Sample A portion or subset of the population. • Example: 1. Live 5 News surveyed 1000 people as they exited the polls. x x xx x x x xx x x xx x xx x x xx x x x x x 2. Your Turn x Ch 1 Larson/Farber x 6

What is Data? Data: Consist of information coming from observations, counts, measurements, or responses. Ø Examples: Population 1. The number of peoples living in cities in the low country SC 2. The number of car dealership Summerville SC Ch 1 Larson/Farber 7

What is Data? (Peer Talk) Peer Talk: Turn to your neighbor Identify a category (ex: basketball) Generate 3 examples of data in the category Ch 1 Larson/Farber 8

Population Sample In a recent survey, 3002 adults in the United States were asked if they read news on the internet at least once a week. 600 of the adults said yes. Ch 1 Larson/Farber 9

Important Terms • Parameter: A number that describes a population characteristic. Example: Average gross income of all people in the United States in 2002. • Statistic: A number that describes a sample characteristic. Example: 2002 gross income of people from a sample of three states. Ch 1 Larson/Farber 10

Parameter vs Statistics Determine if the numerical value represents a parameter or a statistic. In a random check of a sample of groceries stores, the FDA found that 34% of the stores were not storing fish at the proper temperature. A survey of 1, 068 students was taken from Clemson University which has 19, 000 students. Only 54% claimed to enjoy the food. Ch 1 Larson/Farber 11

Parameter vs Statistics Determine if the numerical value represents a parameter or a statistic. In a recent year, the average Math scores for all graduates on the ACT was 20. 7. In a recent year, the interest category for 12% of all new magazines was sports. Ch 1 Larson/Farber 12

Two Branches of Statistics Descriptive Statistics Involves organizing, summarizing, and displaying data. Example: 1. Based on the 2010 census, 40. 5 millions households have two vehicles. 2. The average annual salary for an NFL player for the year 2014 was $1, 100, 500. Ch 1 Larson/Farber 13

Two Branches of Statistics Inferential Statistics Involves using sample data to draw conclusions about a population. Example: 1. From past figures, it is projected that fewer students will drop out of school at ARHS this year. Ch 1 Larson/Farber 14

Descriptive vs Inferential The average of the students in your statistics class is 19 years. Does this statement describe a Descriptive Statistics or an Inferential Statistics From past figures, it is predicted that 56% of the registered voters in California will vote in the June primary. Does this statement describe a Descriptive Statistics or an Inferential Statistics A recent survey shows that people believe the local weathermen are wrong often. Is this a descriptive or inferential statistic? Ch 1 Larson/Farber 15

Closing Pick a term and describe it. Parameter Inferential Statistics Sample Statistic Descriptive Statistics Population Statistics Ch 1 Larson/Farber 16

Section 1. 2 Data Classification

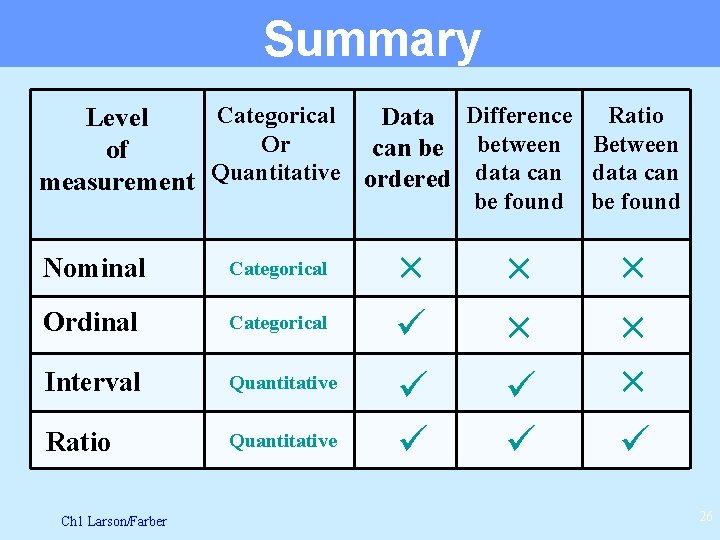
Data Classification A data set can be classified according to the type and the level of measurement: There are two types of data: 1 - Categorical data 2 - Quantitative data There are four levels of measurement: 1. Nominal 2. Ordinal 3. Interval 4. Ratio Ch 1 Larson/Farber 18

Type of Data Categorical data consist of attributes, labels, or non-numerical entries. Examples: The color of shirts, the type of car, the condition of a patient. Ch 1 Larson/Farber 19

Type of Data Quantitative data consist of numerical measurements or counts Examples: Age of students, Number of books in the book bag Ch 1 Larson/Farber 20

Levels of Measurement A data set can be classified according to the highest level of measurement that applies. The four levels of measurement, listed from lowest to highest are: 1. Nominal 2. Ordinal 3. Interval 4. Ratio Ch 1 Larson/Farber 21

Levels of Measurement 1. Nominal: Categories, names, labels, or qualities. Cannot perform mathematical operations on this data. Ex: type of car you drive, your major Ch 1 Larson/Farber 22

Levels of Measurement 2. Ordinal: Data can be arranged in order. You can say one data entry is greater than another. 1 st place Ex: TV ratings, condition of patient in hospital. Ch 1 Larson/Farber 23

Levels of Measurement 3. Interval: Data can be ordered and differences between 2 entries can be calculated. There is no inherent zero (a zero that means “none”. ) Ex: Temperature, year of birth Ch 1 Larson/Farber 24

Levels of Measurement 4. Ratio: There is an inherent zero. Data can be ordered, differences can be found, and a ratio can be formed so you can say one data value is a multiple of another. Ex. Height, weight, age Ch 1 Larson/Farber 25

Summary Categorical Data Difference Ratio Level Or can be between Between of measurement Quantitative ordered data can be found × × × Nominal Categorical × Ordinal Categorical ü × × Interval Quantitative Ratio Quantitative ü ü Ch 1 Larson/Farber ü 26

Section 1. 3 Experimental Design

Random Sample: Each member of the population has an equal chance of being selected. Simple Random Sample: All samples of the same size are equally likely. x x xxxx x x xx xx xx x x x x xx x xxxx x x x x x x xx xx xx x üAssign a number to each member of the population. üRandom numbers can be generated by a random number table, software program or a calculator. üData from members of the population that correspond to these numbers become members of the sample.

Stratified Random Samples Divide the population into groups (strata) and select a random sample from each group. Strata could be age groups, genders or levels of education, for example. Example: Sample A study on students behavior is conducted. The students are divided into grade level. Then a random sample of Each grade level is selected and interviewed Ch 1 Larson/Farber 29

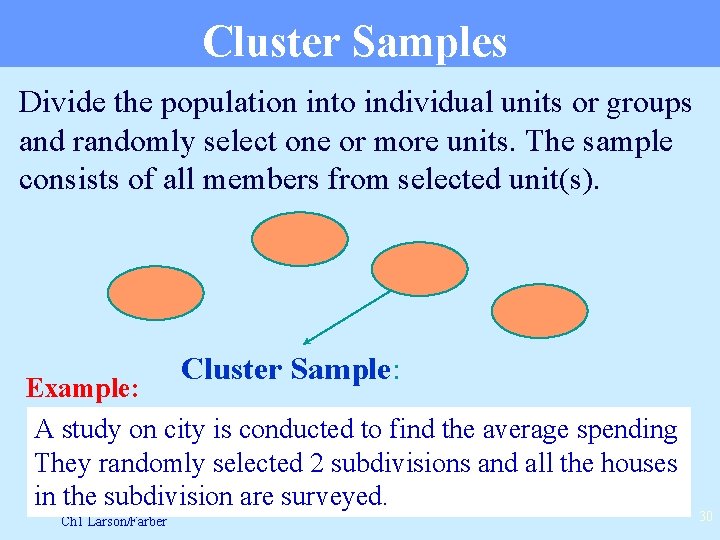
Cluster Samples Divide the population into individual units or groups and randomly select one or more units. The sample consists of all members from selected unit(s). Cluster Sample: Example: A study on city is conducted to find the average spending They randomly selected 2 subdivisions and all the houses in the subdivision are surveyed. Ch 1 Larson/Farber 30

Systematic Samples Choose a starting value at random. Then choose sample members at regular intervals. xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx We say we choose every kth member. In this example, k = 5. Every 5 th member of the population is selected. Example: Law enforcement officials stops and check the driver of Every third vehicle for blood and alcohol content. Ch 1 Larson/Farber 31

Other Samples Convenience Sample: Choose readily available members of the population for your sample. Example: A student ask 18 friends to participate in a psychology experiment Ch 1 Larson/Farber 32

Data Collection There are several ways to collect data: • Observation In an observational study, the observer observes and Measures the characteristics of interest. Example: During the change of class a ARHS, a teacher record the number of students who are in dress code violation Ch 1 Larson/Farber 33

Data Collection • Experiment: Apply a treatment to a part of the group and Observe the response. Example: A study of the effect on the human digestive system Of potato chips with fat substitute. Ch 1 Larson/Farber 34

Data Collection • Simulation: Use a mathematical model (often with a computer) to reproduce condition. Example: A study of how fast a virus will spread in region. Ch 1 Larson/Farber 35

Data Collection • Census: A count or measure of the entire population Example: A study of how the salary of all the employee of the Dorchester school district 2 • Sampling: A count or measure of part of the population. Example: A study of the GPA of the top 10% of the students at ARHS Ch 1 Larson/Farber 36