1 Intermediate Code Generation 2 Intermediate Code Generation

1 Intermediate Code Generation

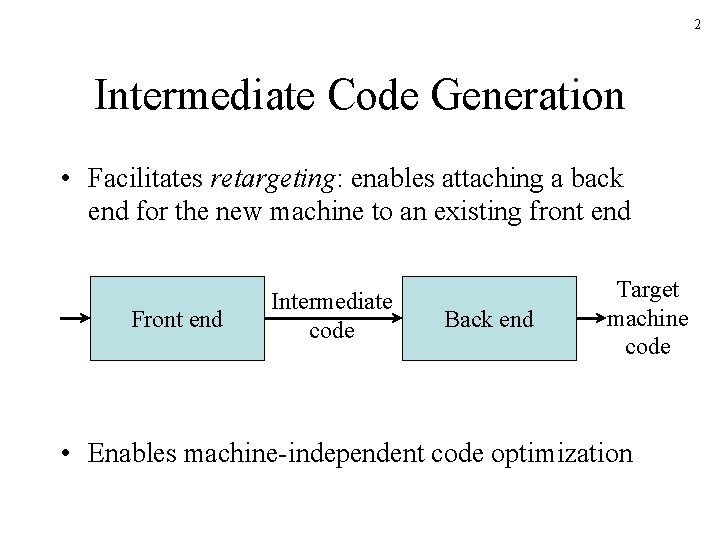
2 Intermediate Code Generation • Facilitates retargeting: enables attaching a back end for the new machine to an existing front end Front end Intermediate code Back end Target machine code • Enables machine-independent code optimization

3 Intermediate Representations • Graphical representations (e. g. AST) • Postfix notation: operations on values stored on operand stack • Three-address code: (e. g. triples and quads) x : = y op z

4 Three-Address Statements • • Assignment statements: x : = y op z, x : = op y Indexed assignments: x : = y[i], x[i] : = y Pointer assignments: x : = &y, x : = *y, *x : = y Copy statements: x : = y Unconditional jumps: goto lab Conditional jumps: if x relop y goto lab Function calls

5 Syntax-Directed Translation of Abstract Syntax Trees Production S id : = E E E 1 + E 2 E E 1 * E 2 E - E 1 E ( E 1 ) E id Semantic Rule S. nptr : = mknode(‘: =’, mkleaf(id, id. entry), E. nptr) E. nptr : = mknode(‘+’, E 1. nptr, E 2. nptr) E. nptr : = mknode(‘*’, E 1. nptr, E 2. nptr) E. nptr : = mknode(‘uminus’, E 1. nptr) E. nptr : = E 1. nptr E. nptr : = mkleaf(id, id. entry)

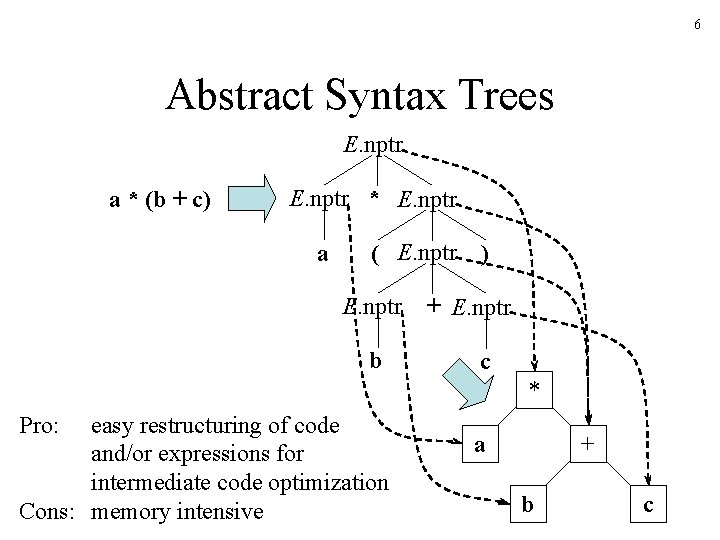
6 Abstract Syntax Trees E. nptr a * (b + c) E. nptr * E. nptr a ( E. nptr b ) + E. nptr c * Pro: easy restructuring of code and/or expressions for intermediate code optimization Cons: memory intensive a + b c

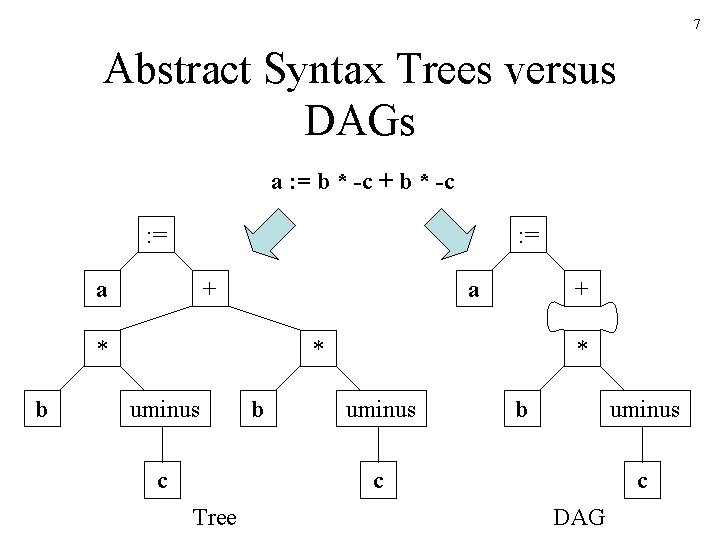
7 Abstract Syntax Trees versus DAGs a : = b * -c + b * -c : = a + a * b + * uminus c b * uminus b uminus c Tree c DAG

8 Postfix Notation a : = b * -c + b * -c a b c uminus * + assign Postfix notation represents operations on a stack Pro: easy to generate Cons: stack operations are more difficult to optimize Bytecode (for example) iload 2 iload 3 ineg imul iadd istore 1 // // // push b push c uminus * + store a

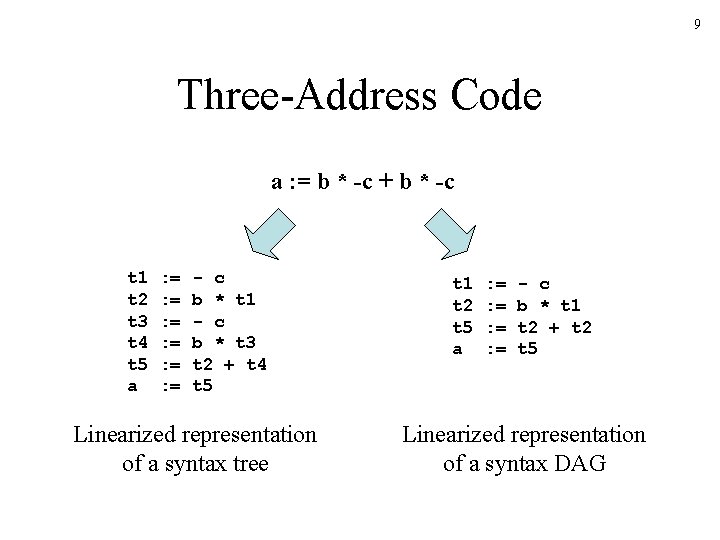
9 Three-Address Code a : = b * -c + b * -c t 1 t 2 t 3 t 4 t 5 a : = : = : = - c b * t 1 - c b * t 3 t 2 + t 4 t 5 Linearized representation of a syntax tree t 1 t 2 t 5 a : = : = - c b * t 1 t 2 + t 2 t 5 Linearized representation of a syntax DAG

Implementation of TAC Statements: Quadruples Ex : a : = b * -c + b * -c # Op Arg 1 Arg 2 Res (0) uminus c (1) * b (2) uminus c (3) * b t 3 t 4 (4) + t 2 t 4 t 5 (5) : = t 5 t 1 t 2 t 3 a Quads (quadruples) Pro: easy to rearrange code for global optimization Cons: lots of temporaries 10

Implementation of TAC Statements: Triples Ex : a : = b * -c + b * -c # Op Arg 1 Arg 2 (0) uminus c (1) * b (2) uminus c (3) * b (2) (4) + (1) (3) (5) : = a (4) (0) Triples Pro: temporaries are implicit Cons: difficult to rearrange code 11

12 Implementation of Three-Address Stmts: Indirect Triples # Stmt # Op Arg 1 (0) (14) uminus c (1) (15) * b (2) (16) uminus c (3) (17) * b (16) (4) (18) + (15) (17) (5) (19) : = a (18) Program Pro: Arg 2 (14) Triple container temporaries are implicit & easier to rearrange code

13 Syntax-Directed Translation into Three-Address Code Production S while E do S 1 S. begin: E. code if E. place = 0 goto S. after S. code Semantic rule goto S. begin : = newlabel() S. after: … S. code : = gen(S. begin ‘: ’) || E. code || gen(‘if’ E. place ‘=‘ ‘ 0’ ‘goto’ S. after) || S 1. code || gen(‘goto’ S. begin) || gen(S. after ‘: ’)

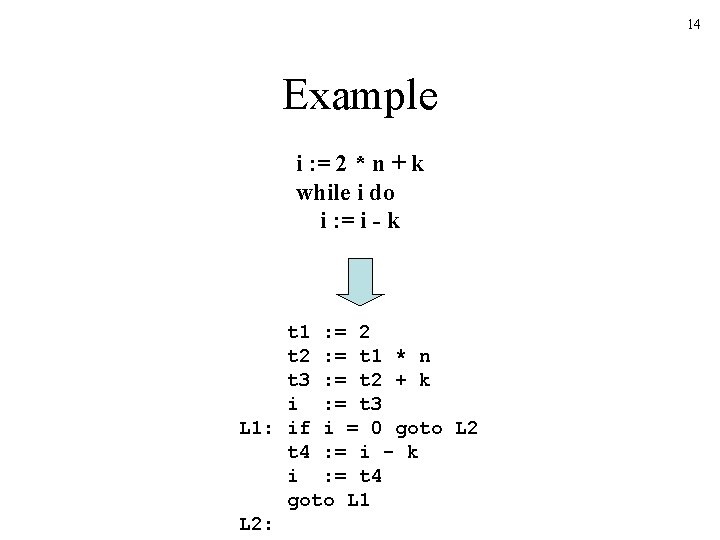
14 Example i : = 2 * n + k while i do i : = i - k t 1 : = 2 t 2 : = t 1 * n t 3 : = t 2 + k i : = t 3 L 1: if i = 0 goto L 2 t 4 : = i - k i : = t 4 goto L 1 L 2:

15 Advanced Intermediate Code Generation Techniques • Reusing temporary names • Addressing array elements • Translating logical and relational expressions • Translating short-circuit Boolean expressions and flow-of-control statements with backpatching lists • Translating procedure calls

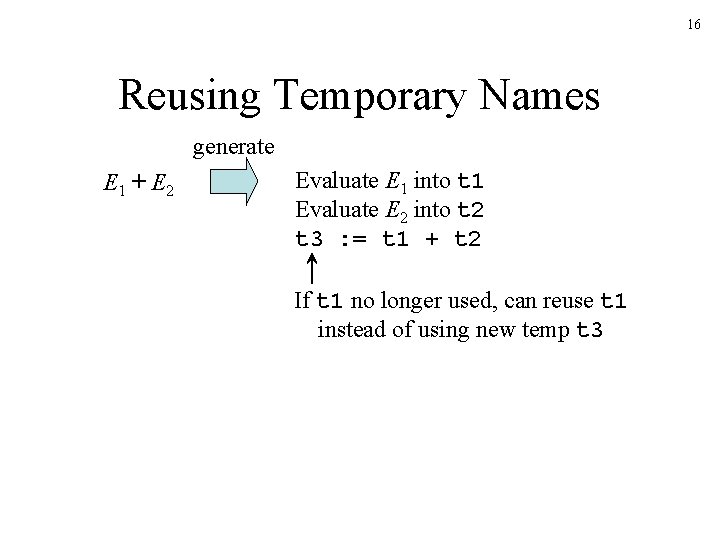
16 Reusing Temporary Names generate E 1 + E 2 Evaluate E 1 into t 1 Evaluate E 2 into t 2 t 3 : = t 1 + t 2 If t 1 no longer used, can reuse t 1 instead of using new temp t 3

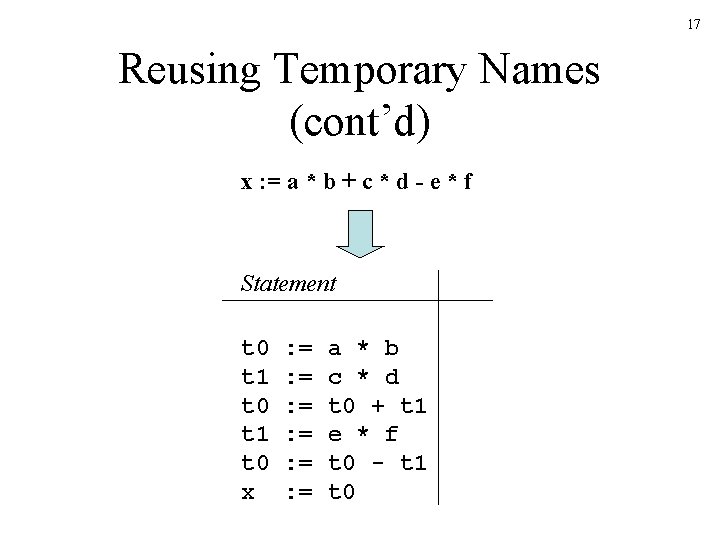
17 Reusing Temporary Names (cont’d) x : = a * b + c * d - e * f Statement t 0 t 1 t 0 x : = : = : = a * b c * d t 0 + t 1 e * f t 0 - t 1 t 0

18 Addressing Array Elements: One. Dimensional Arrays A : array [10. . 20] of integer; … : = A[i] = base. A + (i - low) * w =i*w+c where c = base. A - low * w with low = 10; w = 4 t 1 t 2 t 3 … : = : = c // c = i * 4 t 1[t 2] t 3 base. A - 10 * 4

19 Addressing Array Elements: Multi-Dimensional Arrays A : array [1. . 2, 1. . 3] of integer; low 1 = 1, low 2 = 1, n 1 = 2, n 2 = 3, w = 4 base. A A[1, 1] A[1, 2] A[2, 1] A[1, 3] A[1, 2] A[2, 1] A[2, 2] A[1, 3] A[2, 3] Row-major Column-major

20 Addressing Array Elements: Multi-Dimensional Arrays A : array [1. . 2, 1. . 3] of integer; (Row-major) … : = A[i, j] = base. A + ((i 1 - low 1) * n 2 + i 2 - low 2) * w = ((i 1 * n 2) + i 2) * w + c where c = base. A - ((low 1 * n 2) + low 2) * w with low 1 = 1; low 2 = 1; n 2 = 3; w = 4 t 1 t 2 t 3 t 4 … : = : = : = i * 3 t 1 + j c // c = t 1 * 4 t 2[t 3] t 4 base. A - (1 * 3 + 1) * 4

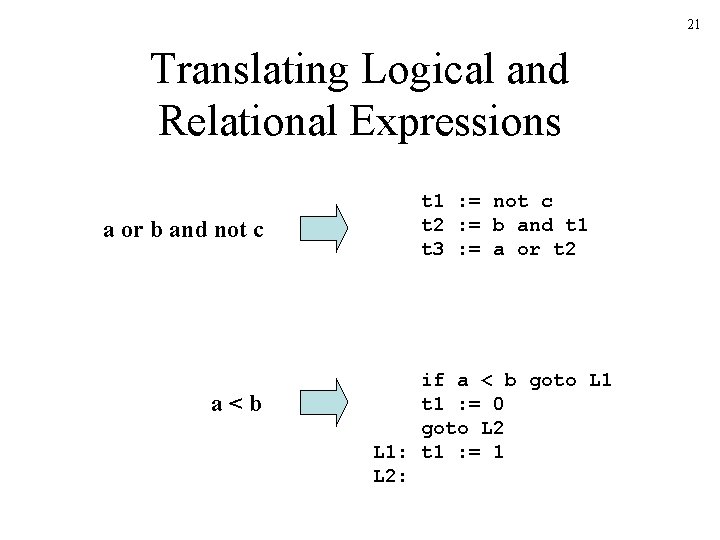
21 Translating Logical and Relational Expressions a or b and not c a<b t 1 : = not c t 2 : = b and t 1 t 3 : = a or t 2 if a < b goto L 1 t 1 : = 0 goto L 2 L 1: t 1 : = 1 L 2:

22 Backpatch Operations with Lists • makelist(i) creates a new list containing threeaddress location i, returns a pointer to the list • merge(p 1, p 2) concatenates lists pointed to by p 1 and p 2, returns a pointer to the concatenates list • backpatch(p, i) inserts i as the target label for each of the statements in the list pointed to by p

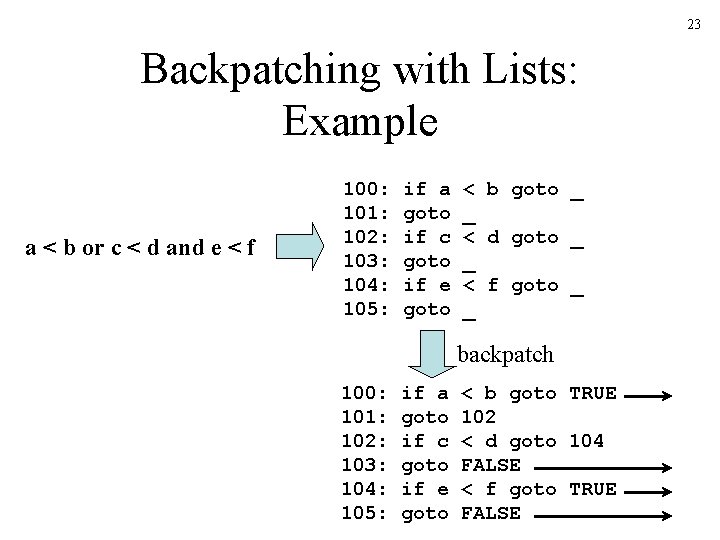
23 Backpatching with Lists: Example a < b or c < d and e < f 100: 101: 102: 103: 104: 105: if a goto if c goto if e goto < b goto _ _ < d goto _ _ < f goto _ _ backpatch 100: 101: 102: 103: 104: 105: if a goto if c goto if e goto < b goto TRUE 102 < d goto 104 FALSE < f goto TRUE FALSE

24 Translating Procedure Calls S call id ( Elist ) Elist , E |E foo(a+1, b, 7) t 1 : = a + 1 t 2 : = 7 param t 1 param b param t 2 call foo 3