1 ICT Foundations of Propositional Logic Copyright 2010

1 ICT Foundations of Propositional Logic Copyright © 2010, Copyright IT Gatekeeper – Ohiwa Lab. All rights © 2010, Project IT Gatekeeper Project – Ohiwa Lab. reserved. All rights reserved.

2 Why to learn Logic? • As a basis in computer science ▪ For understanding the logic circuits being used in computer ▪ This lecture introduces the basis of Logic circuits ▪ Logic is also an important concept in programming • As a general knowledge of college students ▪ Recommend those who want to study more specifically to take other related courses ▪ E. g. : Mathematics and Logic, Functional Calculation Theory, etc. • As an useful tool for many things ▪ To solve many fundamental questions of logic problems in the company entrance exam SPI（Synthetic Personality Inventory） ▪ Logic formula approach can be applied to Web search engine Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

3 What is a Proposition? • A proposition or Statement is a sentence which is either true or false (not be a question, or an imperative sentence). ▪ Whale is a mammal. 　→　true (always precise) ▪ Aristotle is great. → false (“great” is not clear) • Examples of proposition: ○ I am a student. ○ Dog has four legs. ○ School was canceled yesterday. × How old are you? × Clean up your room! Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

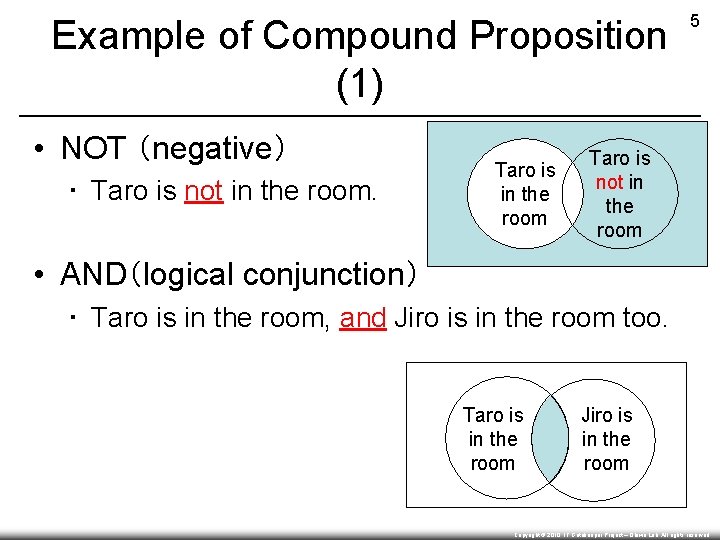
Simple Proposition and Compound Proposition 4 • Simple proposition ▪ does not contain negative words or conjunctions ▪ E. g. : I am a student. • Compound proposition ▪ contains conjunctions (and, or, but, if, equal to) or negative words (not) ▪ E. g. : Taro is in the room and Jiro is in the room too. ※”equal to” is not addressed in this lecture Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

Example of Compound Proposition (1) • NOT （negative） ▪ Taro is not in the room. Taro is in the room 5 Taro is not in the room • AND（logical conjunction） ▪ Taro is in the room, and Jiro is in the room too. Taro is in the room Jiro is in the room Q Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

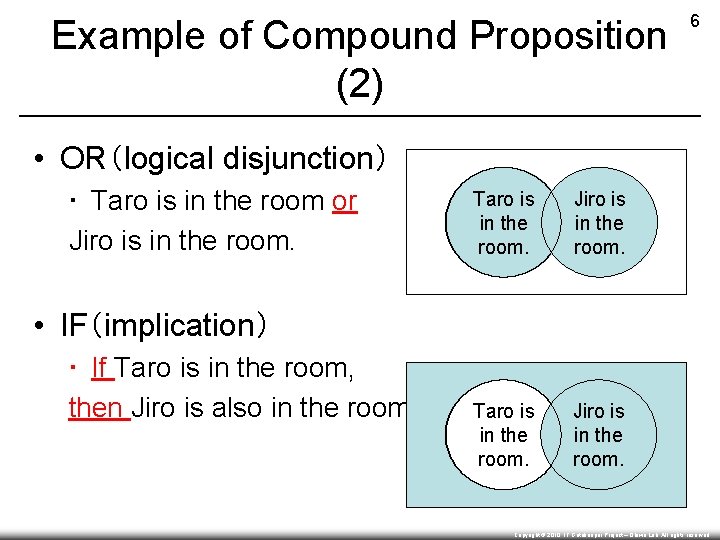
Example of Compound Proposition (2) 6 • OR（logical disjunction） ▪ Taro is in the room or Jiro is in the room. Taro is in the room. Jiro is in the room. • IF（implication） ▪ If Taro is in the room, then Jiro is also in the room. Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

7 Note for Disjunction • “Taro is in the room, or Jiro is in the room” ⇒If Taro and Jiro are in the room, this proposition is true (inclusive disjunction). Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

8 Note for Implication • For example, with compound proposition “If tomorrow is a national holiday, ICT foundation class will be cancelled. There’re four possible cases: （1）Tomorrow is a national holiday, ICT foundation class is cancelled. ⇒ true （2）Tomorrow is a national holiday, ICT foundation class is not cancelled. ⇒ false （3）Tomorrow is not a national holiday, ICT foundation class is cancelled. ⇒ true （4）Tomorrow is not a national holiday, ICT foundation class is not cancelled. ⇒ true • At the beginning of the compound proposition “if tomorrow is a national holiday” only “class is cancelled” has been stated, and “tomorrow is not a national holiday” does not assert anything about. Therefore (3) (4) are true. Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

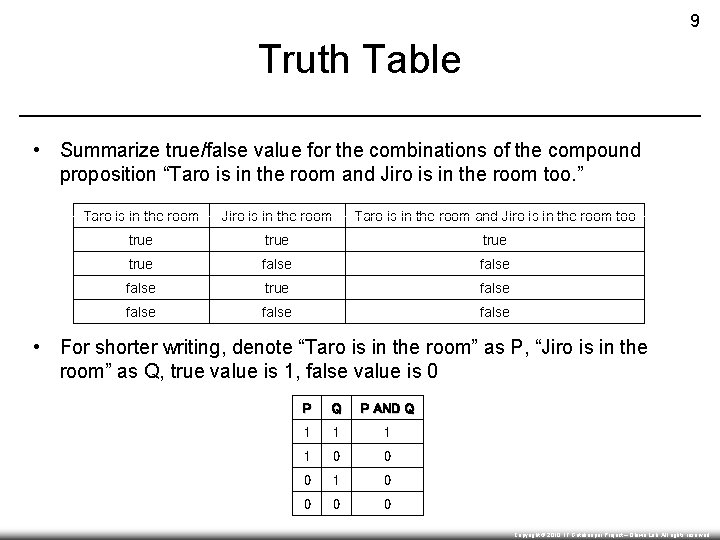
9 Truth Table • Summarize true/false value for the combinations of the compound proposition “Taro is in the room and Jiro is in the room too. ” Taro is in the room Jiro is in the room Taro is in the room and Jiro is in the room too true false true false • For shorter writing, denote “Taro is in the room” as P, “Jiro is in the room” as Q, true value is 1, false value is 0 P Q P AND Q 1 1 0 0 0 1 0 0 Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

10 Truth Function • Truth of a compound proposition is determined as according to the truth of the simple proposition which it is composed. P Q P AND Q 1 1 0 0 0 1 0 0 • Truth of a compound proposition is a function of the truth of the simple proposition. • Truth table represents truth function. Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

11 Summary of the Basic Truth functions • List of symbols (Other notations also exist) ▪ ▪ Negation (NOT)：￢P　 Conjunction（AND）：P∧Q　 Disjunction（OR）：P∨Q 　 Implication (IF…THEN…)：P⇒Q　 P 1 1 0 Q 1 0 1 ￢P 0 0 1 P∧Q 1 0 0 P∨Q 1 1 1 P⇒Q 1 0 0 1 Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

12 【Exercise １】 Conversion Device • Two output devices, P and Q, use the following rules to convert input of 0 and 1: ▪ P: for two incoming signals X 1 & X 2, when at least one of them is 1, the output of P is 1, when both of them are 0, the output of P is 0. ▪ Q：for two incoming signals X 1 & X 2, only when both of them are 1, the output of Q is 1, when one of them are 0, the output of Q is 0. • Connected P & Q as the following circuit ▪ For each incoming signal (X 1, X 2) respectively to P, Q which combinations of (input, output) are correct? a） （X 1, X 2, Y）＝（1, 0, 1） （X 1，X 2） P Q P b） （X 1, X 2, Y）＝（1, 0, 0） Y c） （X 1, X 2, Y）＝（0, 1, 1） d） （X 1, X 2, Y）＝（0, 1, 0） Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

13 ICT Foundation Applied to Web Searching Copyright © 2010, Copyright IT Gatekeeper – Ohiwa Lab. All rights © 2010, Project IT Gatekeeper Project – Ohiwa Lab. reserved. All rights reserved.

14 Search Engine • System that provides searching service to Web page. ▪ Full text search type • Search by input keywords • Display result pages containing the keywords. • E. g. : Google uses keywords to search web page ▪ Directory search type • Classify web pages by keywords • E. g. : From Category of Yahoo to search Web page Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

15 Search using Logical Formulas • Google, for instance, a full-text search service uses logical formulas to do a search efficiently. • Google search form ▪ It is possible to use an own form for searching, but using logical formulas makes it easy to write. Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

Search using Logical Formulas (1) AND Search 16 • AND Search ▪ Input: Keyword 1 AND Keyword 2　 ▪ Find pages that contain both of these keywords ▪ Add keyword AND to narrow the search results • Generally, space can be used to express AND（only input ○○ △△） ▪ For example: SLR cheapest sony Keyword 1 Keyword 2 Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

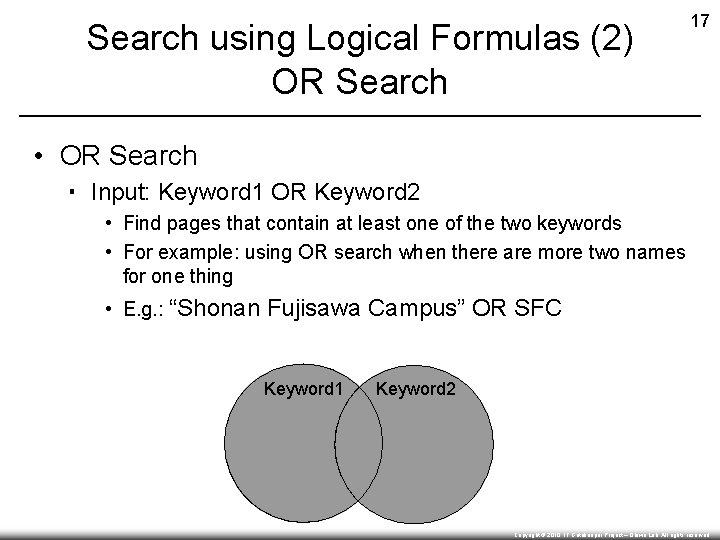
Search using Logical Formulas (2) OR Search 17 • OR Search ▪ Input: Keyword 1 OR Keyword 2 • Find pages that contain at least one of the two keywords • For example: using OR search when there are more two names for one thing • E. g. : “Shonan Fujisawa Campus” OR SFC Keyword 1 Keyword 2 Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

Search using Logical Formulas (3) NOT Search 18 • NOT search ▪ Input: Keyword 1 NOT Keyword 2 ▪ Among pages contain ○○，remove pages △△ ▪ Official written is Keyword 1 AND NOT Keyword 2, but general written omits “AND” Keyword 1 Keyword 2 Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

19 ICT Foundation Applied to SPI Copyright © 2010, Copyright IT Gatekeeper – Ohiwa Lab. All rights © 2010, Project IT Gatekeeper Project – Ohiwa Lab. reserved. All rights reserved.

20 SPI • Synthetic Personality Inventory ▪ Inspection is widely adopted for deciding the employees. ▪ The synthesis aptitude test which is utilized two sides of the ability aspect and the character aspect is used to measure personal talent. ▪ There are many questions about “proposition” and “inference” for ability and character inspection tests. Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

21 Converse, Inverse, Contrapositive • Original proposition：P ⇒ Q • Converse：Q ⇒ P • Inverse：￢ P ⇒ ￢Q • Contrapositive：￢Q ⇒ ￢P ※ If the original proposition is true, the contrapositive is also true. Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

22 Syllogism • Premise 1: ▪ P⇒Q　“Socrates is a human” • Premise 2: ▪ Q⇒R　“All humans die” • Conclusion: ▪ P⇒R　“Socrates dies” Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

【Exercise ２】 Sample question of SPI (1) 23 • The proposition “One who likes chess is good at mathematics” is true. Which are correct among the following: a） One who does not like chess is bad at mathematics. b） One who likes chess likes mathematics. c） One who is good at mathematics likes chess. d） One who is not good at mathematics does not like chess. e） One who like chess likes Go. 手とり足とり就活Book SPI問題集 BEST COLLEGES就職部 著　ミネルヴァ出版企画 2006 Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

【Exercise 3】 Sample question of SPI (2) 24 • Assume these statements are true. ▪ Romanticist is a poet. ▪ One who likes stars likes little birds and flowers. ▪ One who likes flowers is romanticists. • Which of these statements are logically true? a） One who likes little birds like flowers. b） One who likes flowers likes stars. c） A poet likes flowers. d） One who likes little birds is romanticists. e） One who likes stars is a poet. 手とり足とり就活Book SPI問題集 BEST COLLEGES就職部 著　ミネルヴァ出版企画 2006 Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.

【Exercise ４】 Who is the honest convict/prisoner? 25 • In a jail, there are prisoners always respond honestly, and prisoners always tell lie. • Guard wants to screen the honest for giving amnesty, asks this question to each prisoner “Who is honest, who tells lie? ” • Then, there’s threesome answered as the following: • A： ▪ B tells lie. I’m honest so I only tell the truth. • B： ▪ C tells lie. I’m honest. • C： ▪ A and B tell lie. I am? Of course, I’m honest. • For each of A，B，C, answer whether or not an honest man or liar. Copyright © 2010, IT Gatekeeper Project – Ohiwa Lab. All rights reserved.