1 Gratings and the Plane Wave Spectrum EMLAB

1 Gratings and the Plane Wave Spectrum EMLAB

Lecture Outline 2 • Review • Wave vectors • Phase matching at an interface • Electromagnetic behavior at an interface • Waves in periodic media • The plane wave spectrum EMLAB

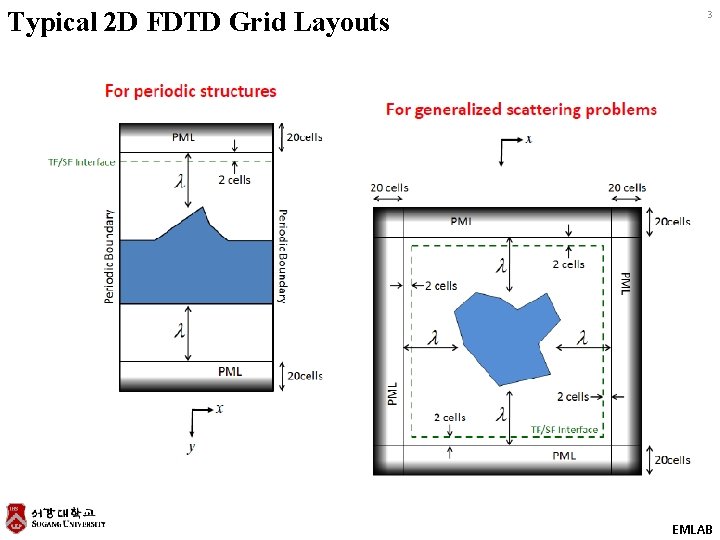
Typical 2 D FDTD Grid Layouts 3 EMLAB

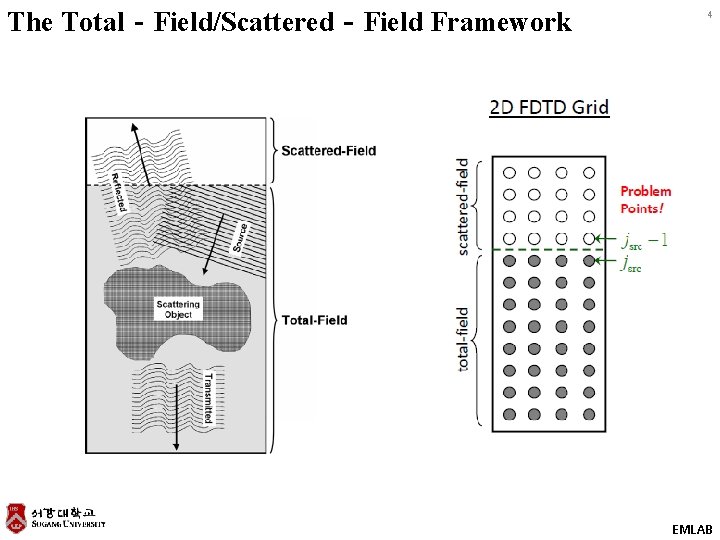
The Total‐Field/Scattered‐Field Framework 4 EMLAB

Corrections to Finite‐Difference Equations at the Problem Cells (Ez Mode) 5 On the scattered‐field side of the TF/SF interface, the curl equation contains a term from the total‐field side. The source must be subtracted from this term to make it look like a scattered‐field quantity. On the total‐field side of the TF/SF interface, the curl equation contains a term from the scattered‐field side. The source must be added to this term to make it look like a total‐field quantity. EMLAB

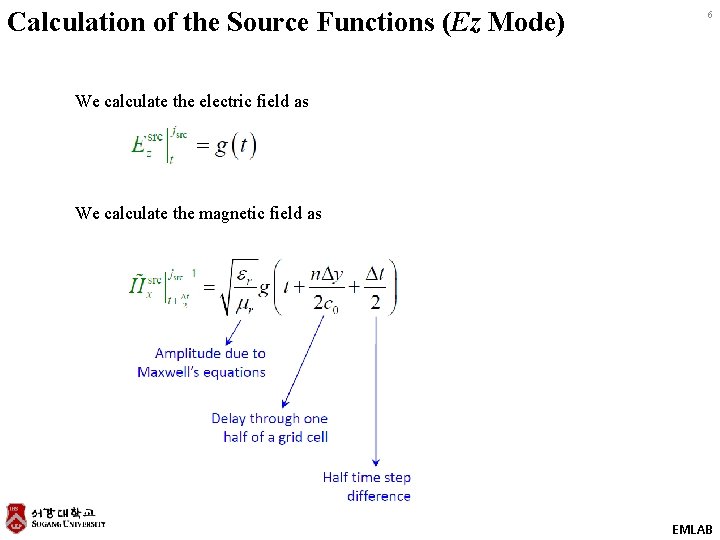
Calculation of the Source Functions (Ez Mode) 6 We calculate the electric field as We calculate the magnetic field as EMLAB

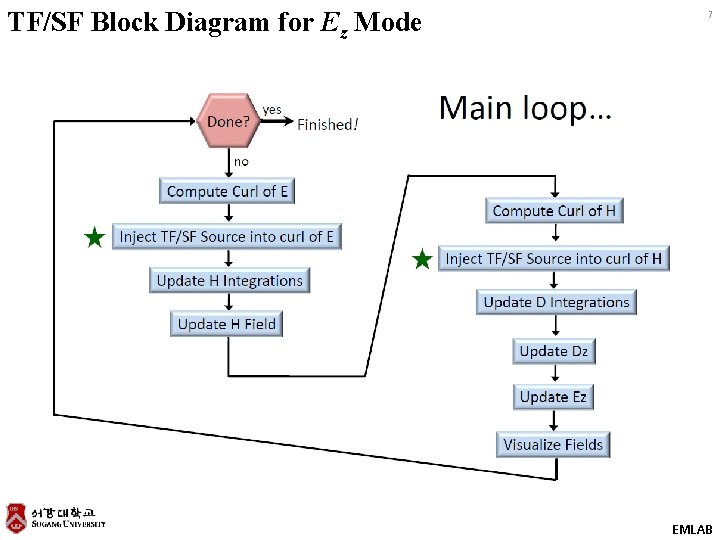
TF/SF Block Diagram for Ez Mode 7 EMLAB

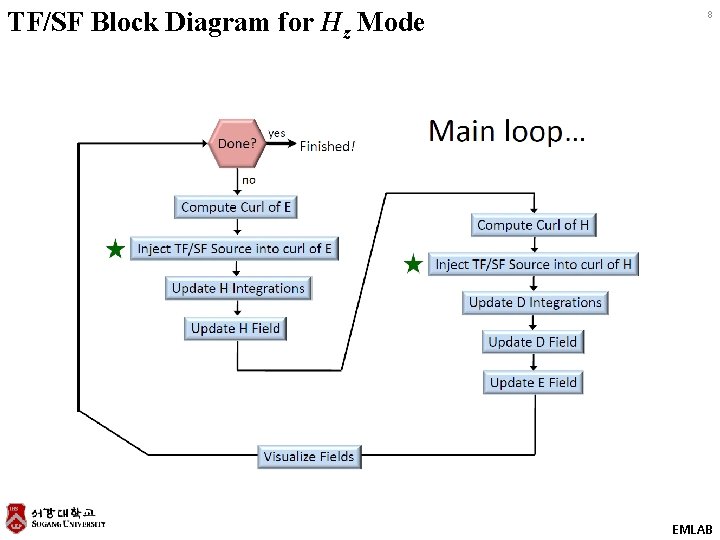
TF/SF Block Diagram for Hz Mode 8 EMLAB

9 Wave Vectors EMLAB

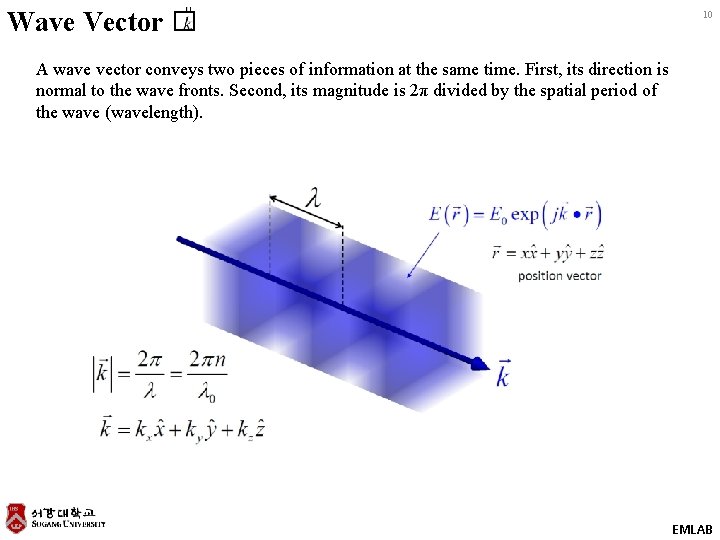
Wave Vector � 10 A wave vector conveys two pieces of information at the same time. First, its direction is normal to the wave fronts. Second, its magnitude is 2π divided by the spatial period of the wave (wavelength). EMLAB

The Complex Wave Vector 11 A wave travelling the +z direction can be written in terms of the wave number k as The wave vector can be complex. We can write it in terms of a real and an imaginary part. Substituting this into or uniform plane wave formula let’s us interpret the real and imaginary parts of k. EMLAB

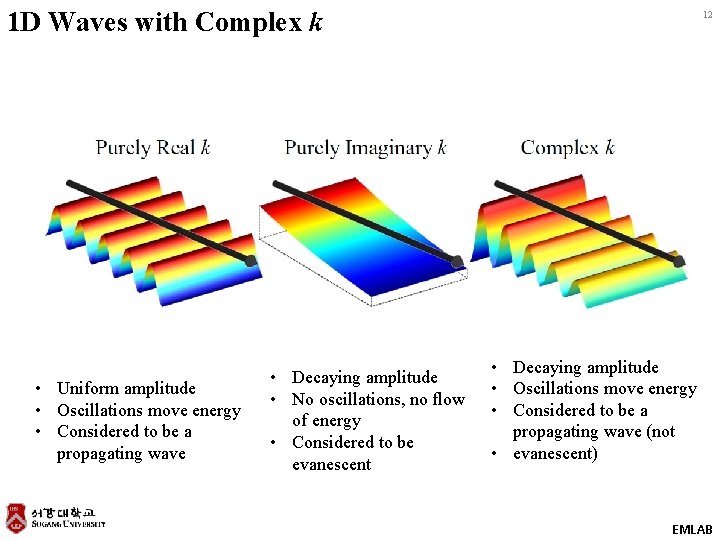
1 D Waves with Complex k • Uniform amplitude • Oscillations move energy • Considered to be a propagating wave • Decaying amplitude • No oscillations, no flow of energy • Considered to be evanescent 12 • Decaying amplitude • Oscillations move energy • Considered to be a propagating wave (not • evanescent) EMLAB

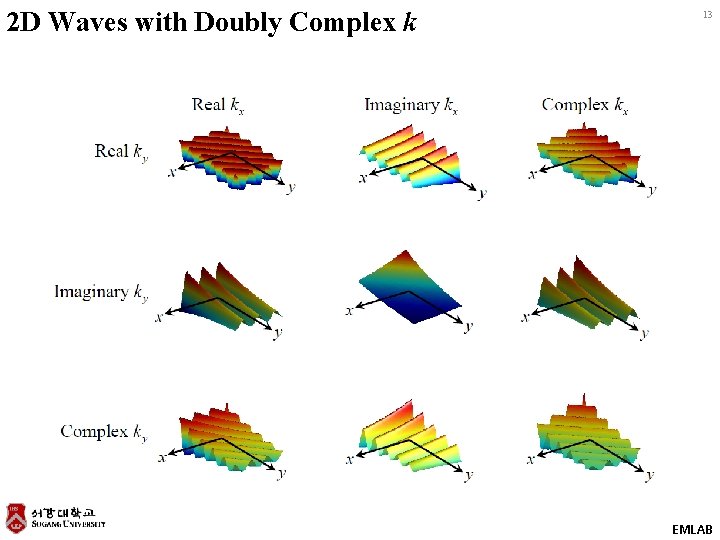
2 D Waves with Doubly Complex k 13 EMLAB

14 Phase Matching at an Interface EMLAB

Dispersion Relation and Index Ellipsoids 15 The dispersion relation for a material relates the wave vector to frequency. Essentially, it tells us the refractive index as a function of direction through the material. For isotropic materials, this is The dispersion relation defines a surface called an “index ellipsoid. ” The vector connecting the origin to a point on the sphere is the k‐vector for that direction from which refractive index can be calculated. This surface is a sphere for isotropic materials. EMLAB

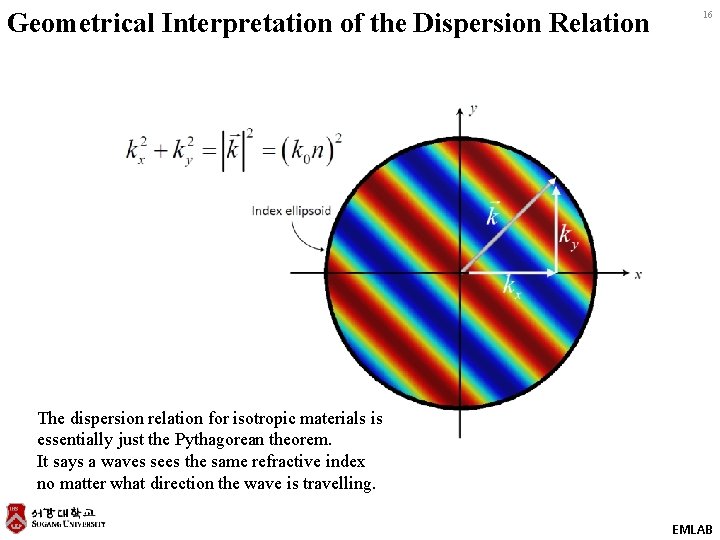
Geometrical Interpretation of the Dispersion Relation 16 The dispersion relation for isotropic materials is essentially just the Pythagorean theorem. It says a waves sees the same refractive index no matter what direction the wave is travelling. EMLAB

Index Ellipsoid in Two Different Materials Material 1 17 Material 2 EMLAB

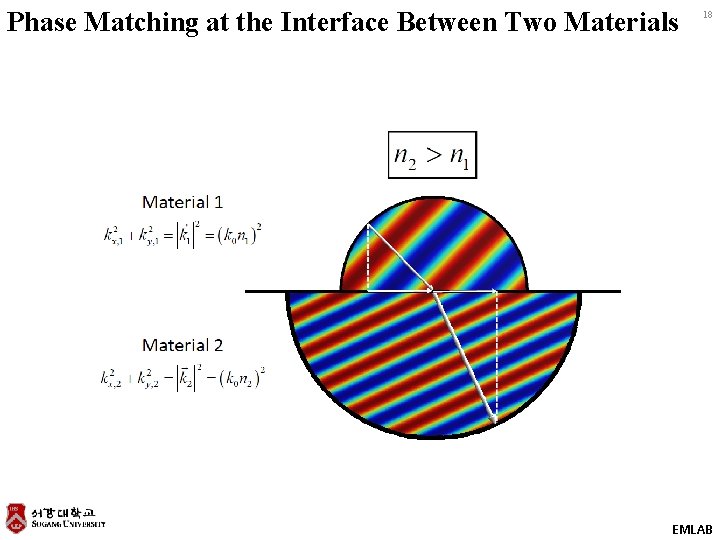
Phase Matching at the Interface Between Two Materials 18 EMLAB

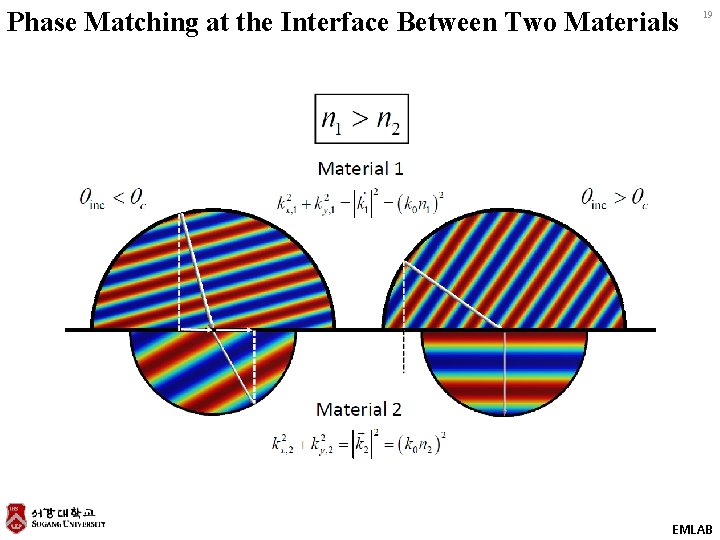
Phase Matching at the Interface Between Two Materials 19 EMLAB

20 Electromagnetic Behavior at an Interface EMLAB

Longitudinal Component of the Wave Vector 21 1. 1. Boundary conditions require that the tangential component of the wave vector is continuous across the interface. Assuming kx is purely real in material 1, kx must be purely real in material 2. ü We have oscillations and energy flow in the x direction. 2. Knowing that the dispersion relation must be satisfied, the longitudinal component of the wave vector in material 2 is calculated from the dispersion relation in material 2. EMLAB

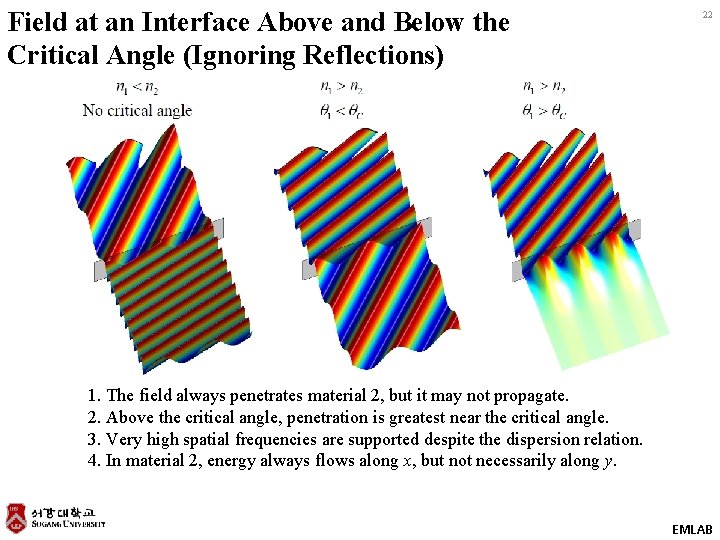
Field at an Interface Above and Below the Critical Angle (Ignoring Reflections) 22 1. The field always penetrates material 2, but it may not propagate. 2. Above the critical angle, penetration is greatest near the critical angle. 3. Very high spatial frequencies are supported despite the dispersion relation. 4. In material 2, energy always flows along x, but not necessarily along y. EMLAB

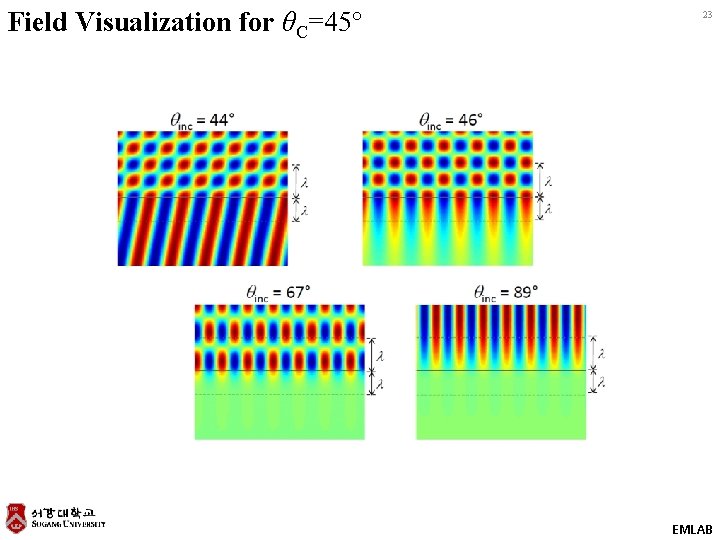
Field Visualization for θC=45° 23 EMLAB

24 Waves in Periodic Media EMLAB

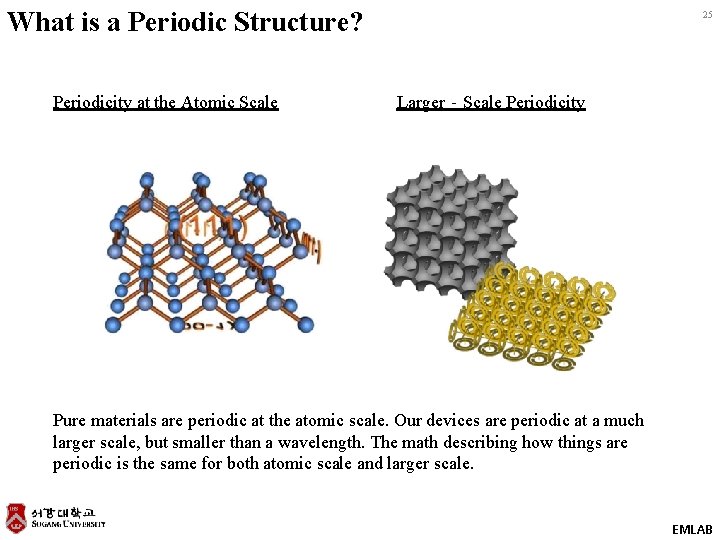
What is a Periodic Structure? Periodicity at the Atomic Scale 25 Larger‐Scale Periodicity Pure materials are periodic at the atomic scale. Our devices are periodic at a much larger scale, but smaller than a wavelength. The math describing how things are periodic is the same for both atomic scale and larger scale. EMLAB

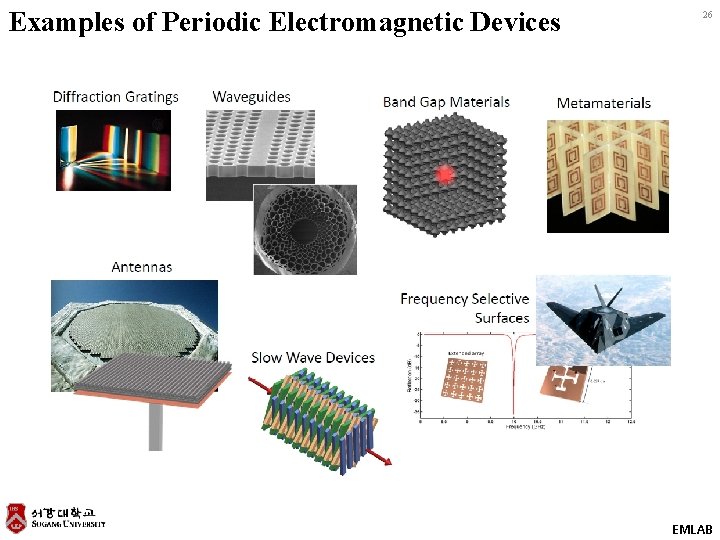
Examples of Periodic Electromagnetic Devices 26 EMLAB

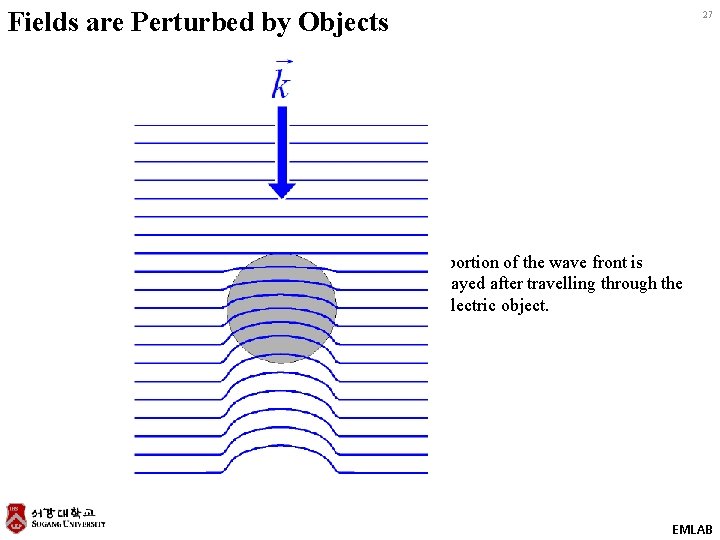
Fields are Perturbed by Objects 27 A portion of the wave front is delayed after travelling through the dielectric object. EMLAB

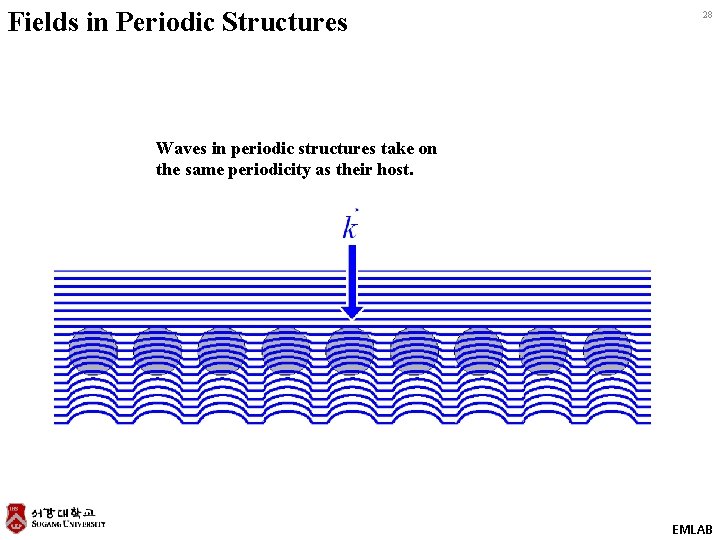
Fields in Periodic Structures 28 Waves in periodic structures take on the same periodicity as their host. EMLAB

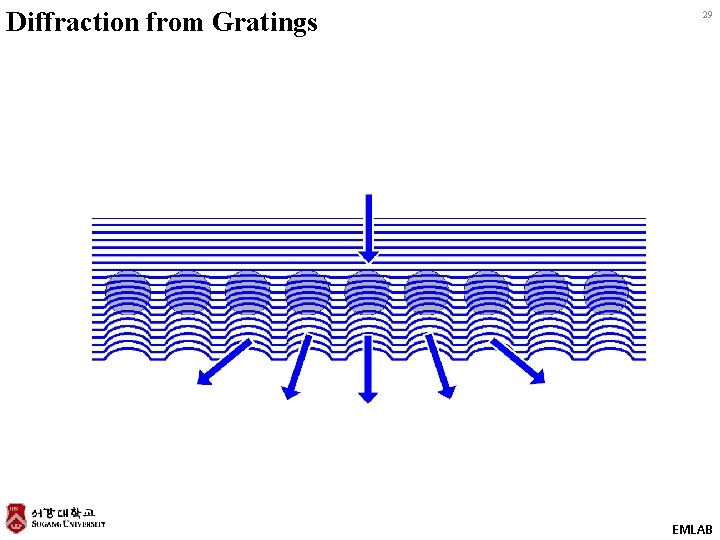
Diffraction from Gratings 29 EMLAB

Grating Equation 30 The angles of the diffracted modes are related to the wavelength and grating through the grating equation. The grating equation only predicts the directions of the modes, not how much power is in them. EMLAB

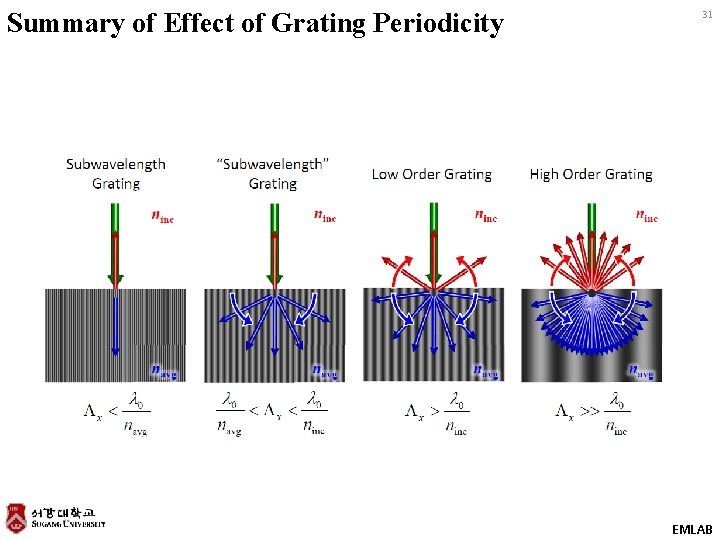
Summary of Effect of Grating Periodicity 31 EMLAB

32 The Plane Wave Spectrum EMLAB

1 D Complex Fourier Series 33 If a function f(x) is periodic with period Λx, it can be expanded into a complex Fourier series. Typically, we retain only a finite number of terms in the expansion. EMLAB

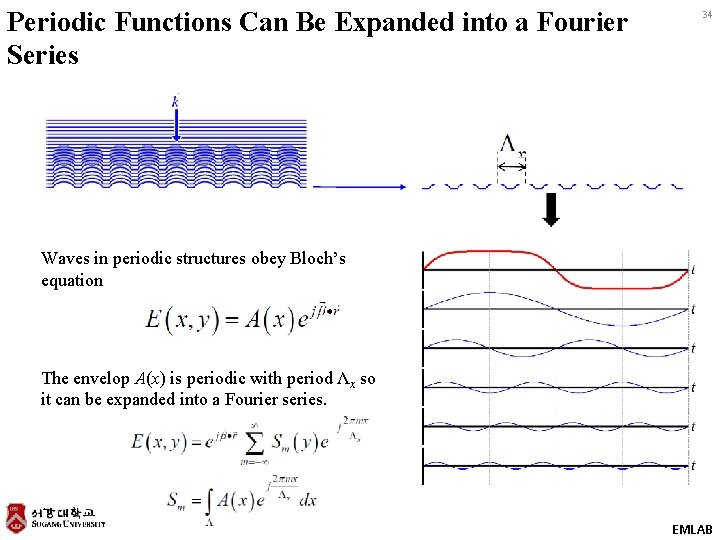
Periodic Functions Can Be Expanded into a Fourier Series 34 Waves in periodic structures obey Bloch’s equation The envelop A(x) is periodic with period Λx so it can be expanded into a Fourier series. EMLAB

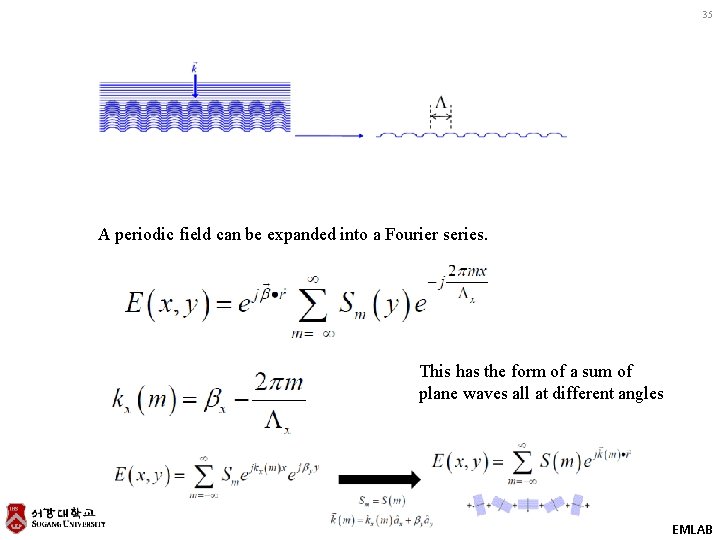
35 A periodic field can be expanded into a Fourier series. This has the form of a sum of plane waves all at different angles EMLAB

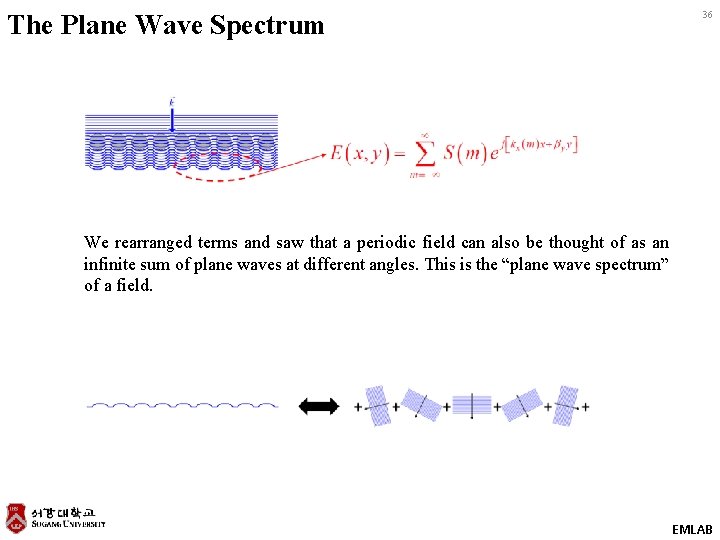
The Plane Wave Spectrum 36 We rearranged terms and saw that a periodic field can also be thought of as an infinite sum of plane waves at different angles. This is the “plane wave spectrum” of a field. EMLAB

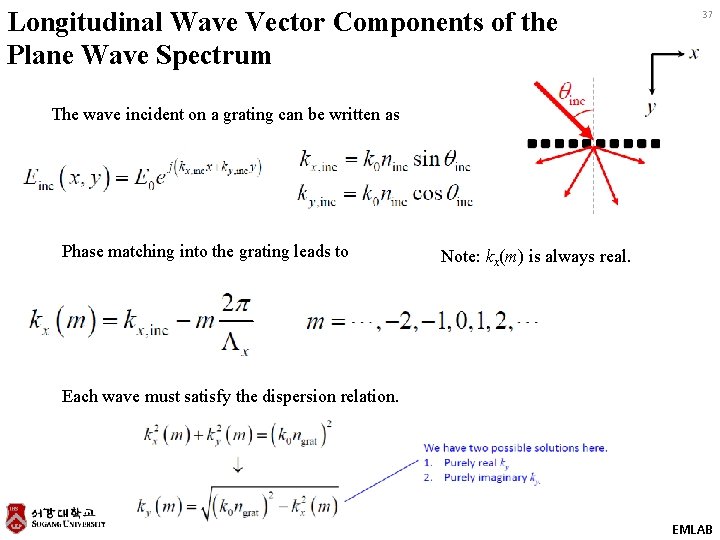
Longitudinal Wave Vector Components of the Plane Wave Spectrum 37 The wave incident on a grating can be written as Phase matching into the grating leads to Note: kx(m) is always real. Each wave must satisfy the dispersion relation. EMLAB

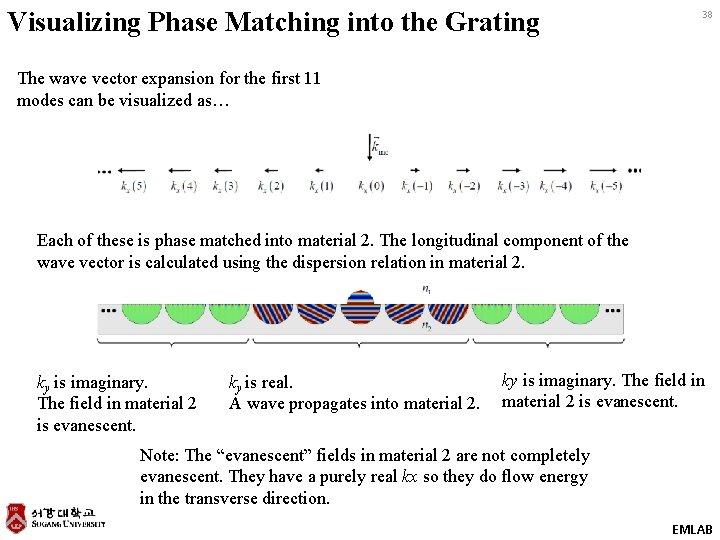
Visualizing Phase Matching into the Grating 38 The wave vector expansion for the first 11 modes can be visualized as… Each of these is phase matched into material 2. The longitudinal component of the wave vector is calculated using the dispersion relation in material 2. ky is imaginary. The field in material 2 is evanescent. ky is real. A wave propagates into material 2. ky is imaginary. The field in material 2 is evanescent. Note: The “evanescent” fields in material 2 are not completely evanescent. They have a purely real kx so they do flow energy in the transverse direction. EMLAB