1 Give an induction definition of the set

1. Give an induction definition of the set S= { π : π is a permutation of {1, 2, 3, …, n} for some integer n ≥ 1 } 2. Use it to prove by induction that the number of permutations on {1, 2, … , n} is equal to n!. 3. Prove that the set S is countable. 1

Lecture 5: Introduction to Graph Theory Introduction to graph theory (review of CSC 225). Many of the hard problems (problems for which we do not have a polynomial time algorithm) studied at the end of the class are questions about graphs. 2

An undirected graph G consists of a set V of vertices and a set E of edges where each edge in E is associated with an unordered pair of vertices from V. The degree of a vertex v is the number of edges incident to v. If (u, v) is in E then u and v are adjacent. A simple graph has no loops or multiple edges. Exercise: prove by induction that a simple graph G on n vertices has at most n(n-1)/2 edges. 3

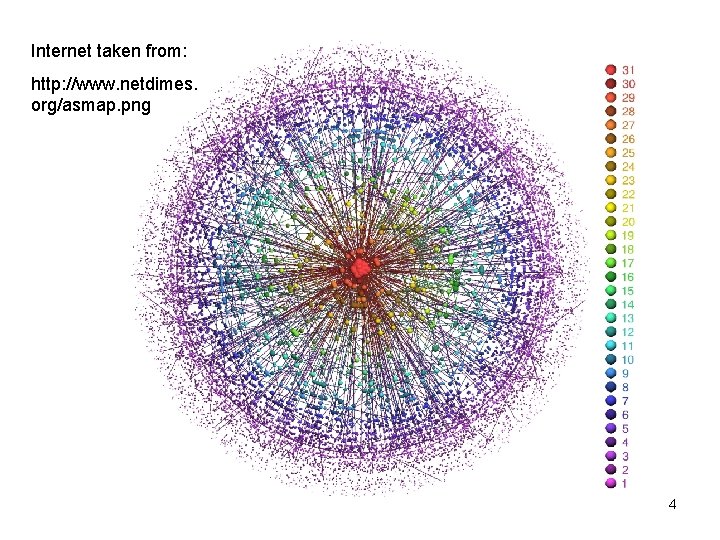
Internet taken from: http: //www. netdimes. org/asmap. png 4

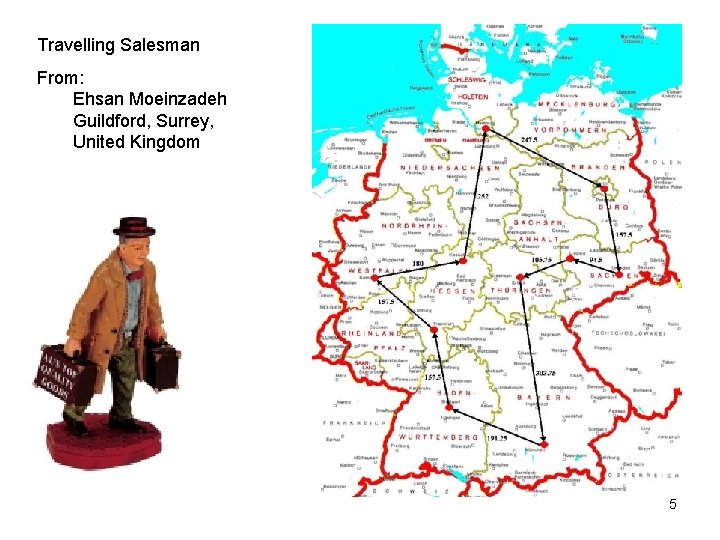
Travelling Salesman From: Ehsan Moeinzadeh Guildford, Surrey, United Kingdom 5

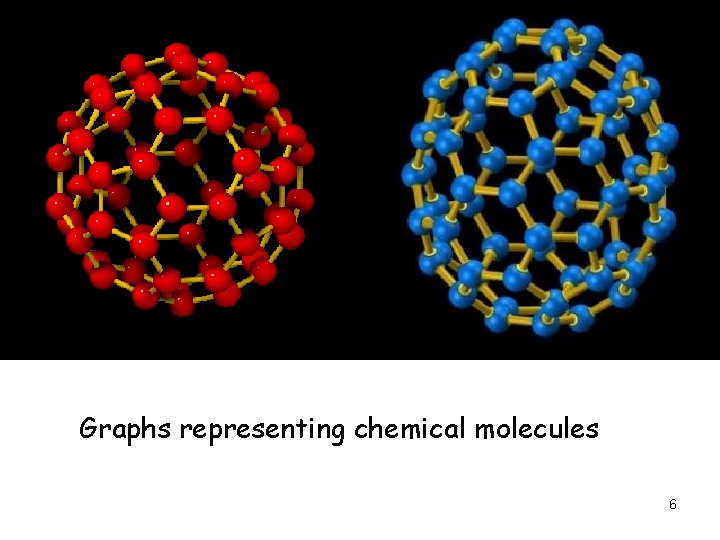
Graphs representing chemical molecules 6

7

A cycle of a graph is an alternating sequence of vertices and edges of the form v 0, (v 0, v 1), v 1, (v 1, v 2), v 2, (v 2, v 3), … , vk-1, (vk-1, vk), vk where except for v 0 = vk the vertices are distinct. Exercise: define path, define connected. A tree is a connected graph with no cycles. A subgraph H of a graph G is a graph with V(H) and E(H) E(G). H is spanning if V(H) = V(G). Spanning tree- spanning subgraph which is a tree. 8

Strange Algorithms Input: a graph G Question: does G have a spanning tree? This can be answered by computing a determinant of a matrix and checking to see if it is zero or not. Don’t make assumptions about what my algorithms for Hamilton Path/Hamilton cycle are doing! Treat them as a black box. 9

Fullerenes • Correspond to 3 -regular planar graphs. • All faces are size 5 or 6. • Euler’s formula: exactly 12 pentagons. 10

Nobel Prize in Chemistry 1996 In 1996, the Nobel Prize in Chemistry was awarded jointly to Robert Curl, Harold Kroto and Richard Smalley for their discovery of fullerenes. Prof Robert F. Curl Jr Photo: P. S. Howell Prof Sir Harold W. Kroto Prof Richard E. Smalley Photo: Prudence Cummings Photo: P. S. Howell, Rice

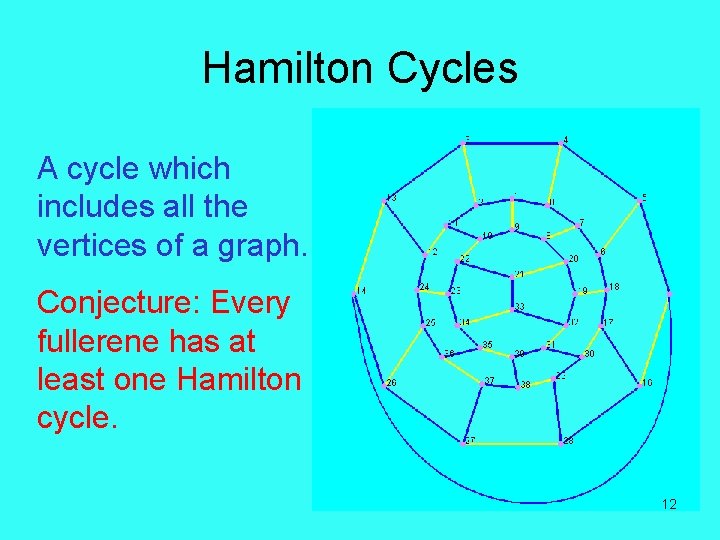
Hamilton Cycles A cycle which includes all the vertices of a graph. Conjecture: Every fullerene has at least one Hamilton cycle. 12

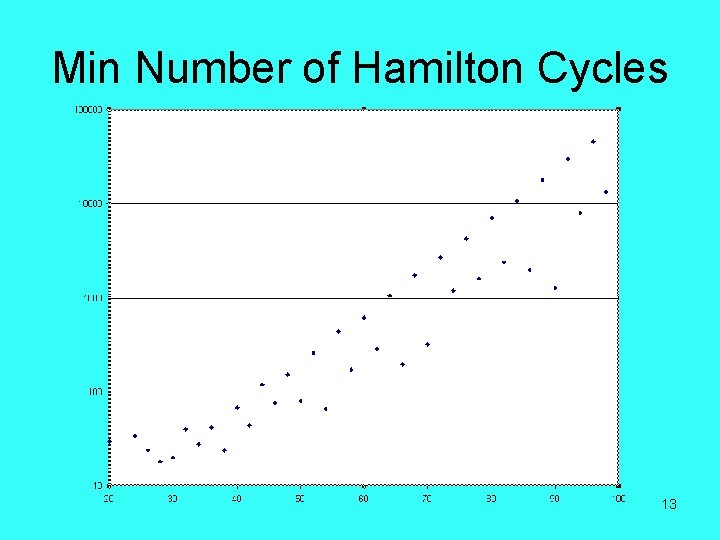
Min Number of Hamilton Cycles 13

Conjecture For all fullerenes except isomer 38: 2, every edge is in at least one Hamilton cycle Isomer 38: 2 14

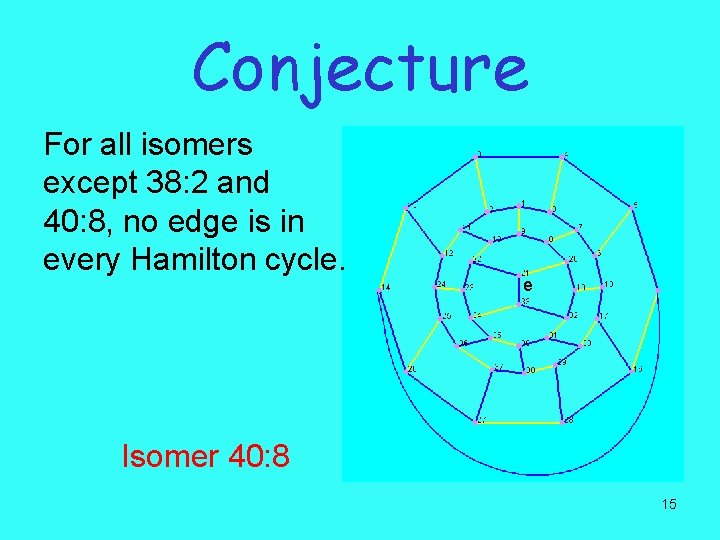
Conjecture For all isomers except 38: 2 and 40: 8, no edge is in every Hamilton cycle. e Isomer 40: 8 15

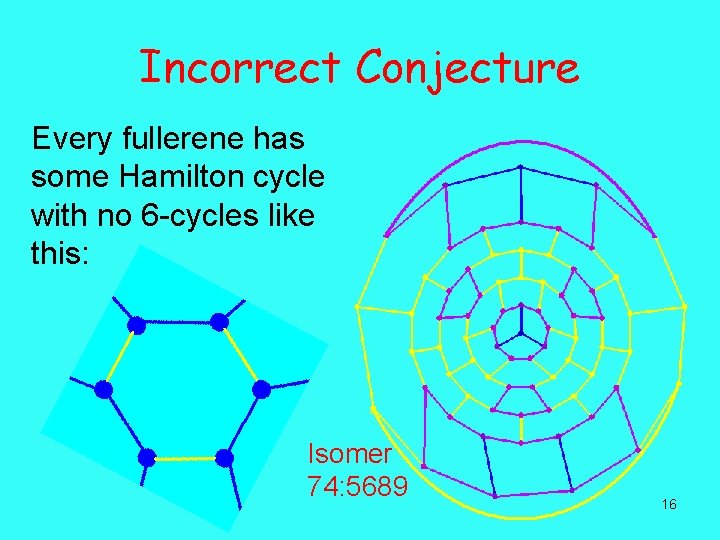
Incorrect Conjecture Every fullerene has some Hamilton cycle with no 6 -cycles like this: Isomer 74: 5689 16

Regular Languages http: //eloquentjavascript. net/img/xkcd_regular_expressions. png 17

Σ* = set of all strings over alphabet Σ Language over Σ – any subset of Σ* Examples: Σ = {0, 1} L 1 = { w Σ* : w has an even number of 0’s} L 2 = { w Σ* : w is the binary representation of a prime number with no leading zeroes} L 3 = Σ* L 4 = { } = Φ L 5 = { ε } 18

Operations on Languages: 1. Complement of L defined over Σ = = { w Σ* : w is not in L } 2. Concatenation of Languages L 1 ۰ L 2 = L 1 L 2 = {w= x۰ y for some x L 1 and y L 2} 3. Kleene star of L, L* = { w= w 1 w 2 w 3 … wk for some k ≥ 0 and w 1, w 2, w 3, … , wk are all in L} 4. L+ = L ۰ L* (Concatenate together one or more strings from L. ) 19