1 Face Recognition using PCA Eigenfaces and LDA

1 Face Recognition using PCA (Eigenfaces) and LDA (Fisherfaces) Pradeep Buddharaju COSC 6397 - Information Assurance U of H

Principal Component Analysis • • A N x N pixel image of a face, represented as a vector occupies a single point in N 2 -dimensional image space. Images of faces being similar in overall configuration, will not be randomly distributed in this huge image space. Therefore, they can be described by a low dimensional subspace. Main idea of PCA (cutler 96): 2 – To find vectors that best account for variation of face images in entire image space. – These vectors are called eigen vectors. – Construct a face space and project the images into this face space (eigenfaces). COSC 6397 - Information Assurance U of H

Image Representation 3 • Training set of images of size N*N are represented by vectors of size N 2 1, 2, 3, …, M Example COSC 6397 - Information Assurance U of H

Average Image and Difference Images 4 • The average training set is defined by Ψ = (1/M) ∑Mi=1 i • Each face differs from the average by vector Φi = Γi – Ψ COSC 6397 - Information Assurance U of H

Covariance Matrix 5 • A covariance matrix is constructed as: C = AAT, where A=[Φ 1, …, ΦM] of size N 2 x N 2 Size of this matrix is N 2 x N 2 • Finding eigenvectors of N 2 x N 2 matrix is intractable. Hence, use the matrix ATA of size M x M and find eigenvectors of this small matrix. Size of this matrix is M*M COSC 6397 - Information Assurance U of H

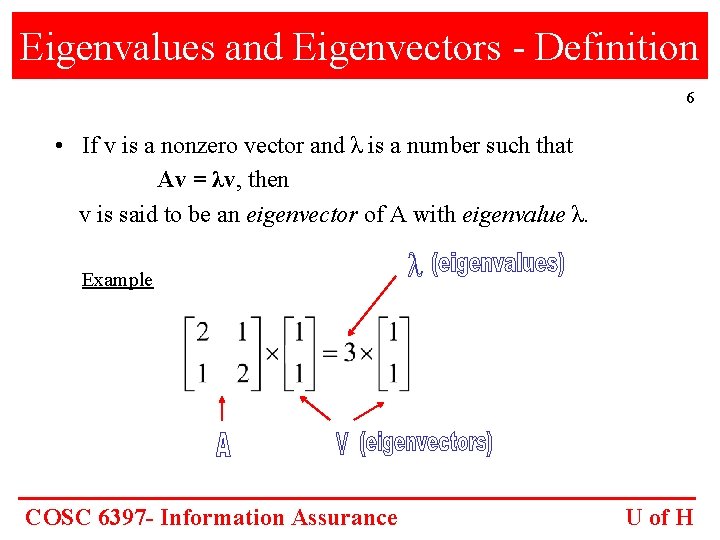
Eigenvalues and Eigenvectors - Definition 6 • If v is a nonzero vector and λ is a number such that Av = λv, then v is said to be an eigenvector of A with eigenvalue λ. Example COSC 6397 - Information Assurance U of H

How to Calculate Eigenvectors? 7 COSC 6397 - Information Assurance U of H

Eigenvectors of Covariance Matrix 8 • The eigenvectors vi of ATA are: • Consider the eigenvectors vi of ATA such that ATAvi = ivi • Premultiplying both sides by A, we have AAT(Avi) = i(Avi) COSC 6397 - Information Assurance U of H

Face Space 9 • The eigenvectors of covariance matrix are ui = Avi • ui resemble facial images which look ghostly, hence called eigenfaces COSC 6397 - Information Assurance U of H

Projection into Face Space 10 • A face image can be projected into this face space by Ωk = UT(Γk – Ψ); k=1, …, M COSC 6397 - Information Assurance U of H

Recognition 11 • The test image, Γ, is projected into the face space to obtain a vector, Ω: Ω = UT(Γ – Ψ) • The distance of Ω to each face class is defined by Єk 2 = ||Ω-Ωk||2; k = 1, …, M • A distance threshold, Өc, is half the largest distance between any two face images: Өc = ½ maxj, k {||Ωj-Ωk||}; j, k = 1, …, M COSC 6397 - Information Assurance U of H

Recognition 12 • Find the distance, Є , between the original image, Γ, and its reconstructed image from the eigenface space, Γf, Є2 = || Γ – Γf ||2 , where Γf = U * Ω + Ψ • Recognition process: – IF Є≥Өc then input image is not a face image; – IF Є<Өc AND Єk≥Өc for all k then input image contains an unknown face; – IF Є<Өc AND Єk*=mink{ Єk} < Өc then input image contains the face of individual k* COSC 6397 - Information Assurance U of H

Limitations of Eigenfaces Approach 13 • Variations in lighting conditions – Different lighting conditions for enrolment and query. – Bright light causing image saturation. • Differences in pose – Head orientation - 2 D feature distances appear to distort. • Expression - Change in feature location and shape. COSC 6397 - Information Assurance U of H

Linear Discriminant Analysis 14 • PCA does not use class information – PCA projections are optimal for reconstruction from a low dimensional basis, they may not be optimal from a discrimination standpoint. • LDA is an enhancement to PCA – Constructs a discriminant subspace that minimizes the scatter between images of same class and maximizes the scatter between different class images COSC 6397 - Information Assurance U of H

Mean Images 15 • Let X 1, X 2, …, Xc be the face classes in the database and let each face class Xi, i = 1, 2, …, c has k facial images xj, j=1, 2, …, k. • We compute the mean image i of each class Xi as: • Now, the mean image of all the classes in the database can be calculated as: COSC 6397 - Information Assurance U of H

Scatter Matrices 16 • We calculate within-class scatter matrix as: • We calculate the between-class scatter matrix as: COSC 6397 - Information Assurance U of H

Projection 17 • • We find the product of SW-1 and SB and then compute the Eigen vectors of this product (SW-1. SB). Use same technique as eigenfaces approach to reduce the dimensionality of scatter matrix to compute eigenvectors. Form a matrix U that represents all eigenvectors of SW-1. SB by placing each eigenvector ui as each column in that matrix. Each face image xj Xi can be projected into this face space by the operation Ωi = UT(xj – ) COSC 6397 - Information Assurance U of H

Testing 18 • Same as Eigenfaces Approach COSC 6397 - Information Assurance U of H

References 19 • Turk, M. , Pentland, A. : Eigenfaces for recognition. J. Cognitive Neuroscience 3 (1991) 71– 86 • Belhumeur, P. Hespanha, J. , Kriegman, D. : Eigenfaces vs. fisherfaces: recognition using class specific linear projection. IEEE Transactions on Pattern Analysis and Machine Intelligence 19 (1997) 711– 720 COSC 6397 - Information Assurance U of H