1 Draw a parse tree for the following

1. Draw a parse tree for the following derivation: S C A C C A b b bb. Bbb bba. Aaabb b b a a bb 2. Show on your parse tree u, v, x, y, z as per the pumping theorem. 3. Prove that the language for this question is an infinite language.

A message from Caitlin Blank (secretary of the Computer Science Course Union): If you haven't heard of the CSCU, check out our webpage (www. cscu. csc. uvic. ca) or visit us at ECS 331. Anyway, we try to make life better by doing awesome things - among said awesome things is this year's Halloween Pub Crawl: October 30 th! $20 gets you into 4 venues (no cover), 3 free drinks, time at a pool table, karaoke, and even busses between venues. It's going to be great, so we hope to see you there! Tickets are on sale now, so for more information email me (cblank@uvic. ca) or stop by the CSCU Office: ECS 331!

Assignment #4 is posted: due on Tues. Nov. 17 (3 weeks from today). Please start early and do not leave it to the night before. Tutorials cancelled this week. The TA will offer an additional session sometime between Dec. 7 -11 to compensate. Final exam tutorial: Monday Dec. 14. Please bring your final exam schedule info to class on Wed. so we can schedule a time for these. Reading break: Tues. /Wed. Nov. 10/11 (no class) No class on Dec. 4: Memorial service 11: 30 am.

Pushdown Automata Picture from: Torsten Schaßan

Pushdown Automata: A pushdown automaton is like a NDFA which has a stack. Every context-free language has a pushdown automaton that accepts it. This lecture starts with some examples, gives the formal definition, then investigates PDA’s further.

Stacks

Stack Data Structure: permits push and pop at the top of the stack.

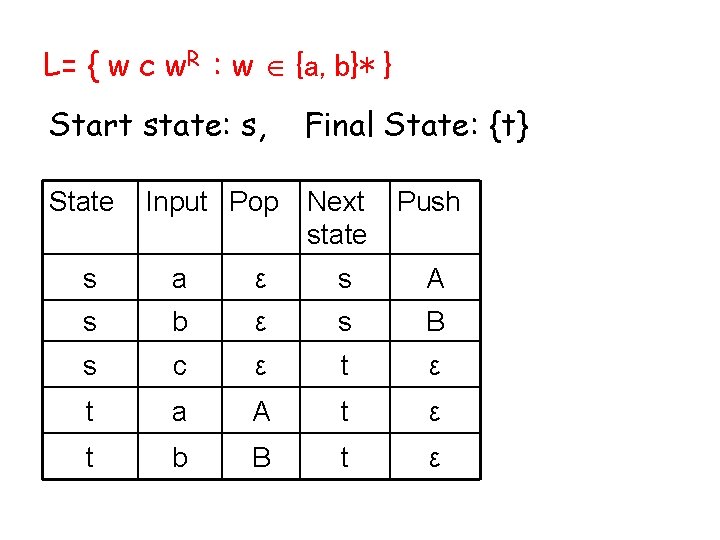
L= { w c w. R : w {a, b}* } Start state: s, Final State: {t} State Next state Push Input Pop s a ε s A s b ε s B s c ε t a A t ε t b B t ε

To accept, there must exist a computation which: 1. Starts in the start state with an empty stack. 2. Applies transitions of the PDA which are applicable at each step. 3. Consumes all the input. 4. Terminates in a final state with an empty stack.

w=abbcbba (s, abbcbba, ε) ├* (s, cbba, BBA)├ (t, bba, BBA) ├* Stack is knocked over like this: (t, ε, ε) B B A A

A pushdown automaton is a sextuple M= (K, Σ, Γ, Δ, s, F) where K is a finite set of states, Σ is an alphabet (the input symbols) Γ is an alphabet (the stack symbols) Δ, the transition relation, is a finite subset of ( K x (Σ⋃ {ε}) x Γ*) x (K x Γ*) state input pop next state push

A configuration of a PDA is a member of K current state x Σ* input remaining x Γ* stack A configuration (q, σ w, α x) ├ (r, w, βx) if ((q, σ, α ), (r, β)) Δ. For M= (K, Σ, Γ, Δ, s, F), L(M) (the language accepted by M) = { w Σ* : (s, w, ε) ├* (f, ε, ε) for some final state f in F}.

L(M)= { w Σ* : (s, w, ε) ├* (f, ε, ε) for some final state f in F}. To accept, there must exist a computation which: 1. Starts in the start state with an empty stack. 2. Applies transitions of the PDA which are applicable at each step. 3. Consumes all the input. 4. Terminates in a final state with an empty stack.

PDA’s are non-deterministic: L= { w w. R : w {a, b}* } Start state: s, Final State: {t} State Next state Push Input Pop s a ε s A s b ε s B s ε ε t a A t ε t b B t ε Guessing wrong time to switch from s to t gives non -accepting computations.

L= {w in {a, b}* : w has the same number of a’s and b’s} Start state: s Final states: {s} State Input Pop s s a a b b ε A ε B Next Push state s B s ε s A s ε

L= {w in {a, b}* : w has the same number of a’s and b’s} State state: s, Final states: {f} State Input Pop s t t t t ε a a a b b b ε ε X A B X Next Push state t X t BX t ε t BB t AX t AA t ε f ε A more deterministic solution: Stack will never contain both A’s and B’s. X- bottom of stack marker.