1 Draw 4 concentric circles 2 Draw an

Central Angle : An Angle whose vertex is at the center of the circle

Semicircle: An Arc that equals 180° E D To name: use 3 letters EDF

You try… 10. 2 Practice B 1 -8 D A E C F B

THINGS TO KNOW AND REMEMBER A circle has 360 degrees A semicircle has 180

measure of an arc = measure of central angle A E Q m AB

Arc Addition Postulate A C B m ABC = m AB + m BC

Tell me the measure of the following arcs. m DAB = 240 m BCA

You try… 10. 2 Practice B 9 – 20 M N O 82 P

Congruent Arcs have the same measure and MUST come from the same circle or

In the same circle, or in congruent circles, two minor arcs are congruent if

If a diameter of a circle is perpendicular to a chord, then the diameter

What can you tell me about segment AC if you know it is the

Ex. 1 If a diameter of a circle is perpendicular to a chord, then

Example 2 EX 2: IN P, if PM AT, PT = 10, and PM

Example 3 In R, XY = 30, RX = 17, and RZ XY. Find

Example 4 IN Q, KL LZ. IF CK = 2 X + 3 and

In the same circle or in congruent circles, two chords are congruent if and

Ex. 6: IN K, K is the midpoint of RE. If TY = -3

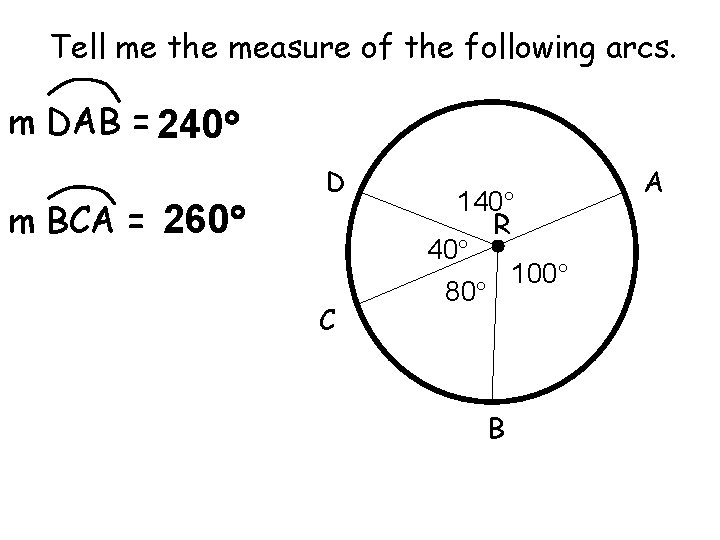
Slides: 26

Download presentation

1. Draw 4 concentric circles 2. Draw an internally tangent line to two circles 3. Name two different types of segments that are equal. 4. Explain the difference between a secant & a chord 5. What do you know about a tangent line and the radius drawn to the point of tangency?

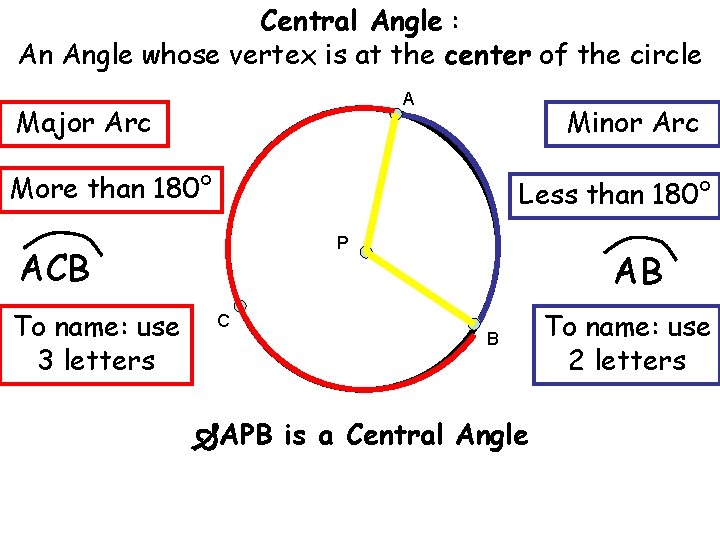
Central Angle : An Angle whose vertex is at the center of the circle A Major Arc Minor Arc More than 180° Less than 180° P ACB To name: use 3 letters C AB B APB is a Central Angle To name: use 2 letters

Semicircle: An Arc that equals 180° E D To name: use 3 letters EDF P F

You try… 10. 2 Practice B 1 -8 D A E C F B

THINGS TO KNOW AND REMEMBER A circle has 360 degrees A semicircle has 180 degrees Vertical Angles are Equal

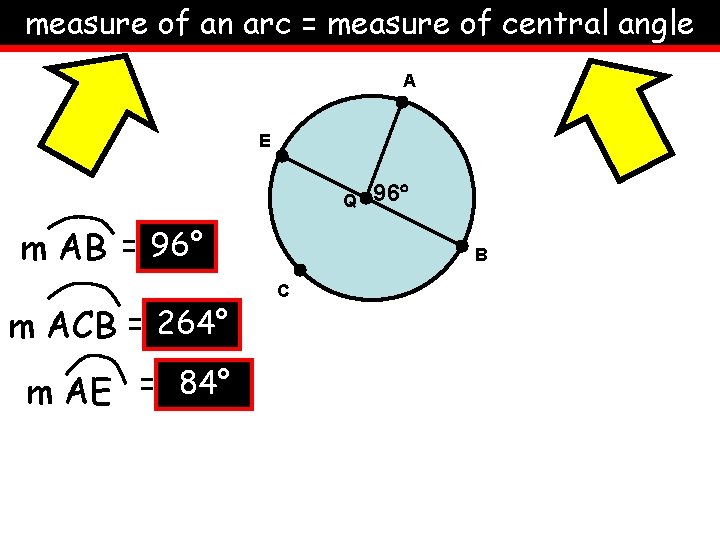
measure of an arc = measure of central angle A E Q m AB = 96° m ACB = 264° m AE = 84° 96 B C

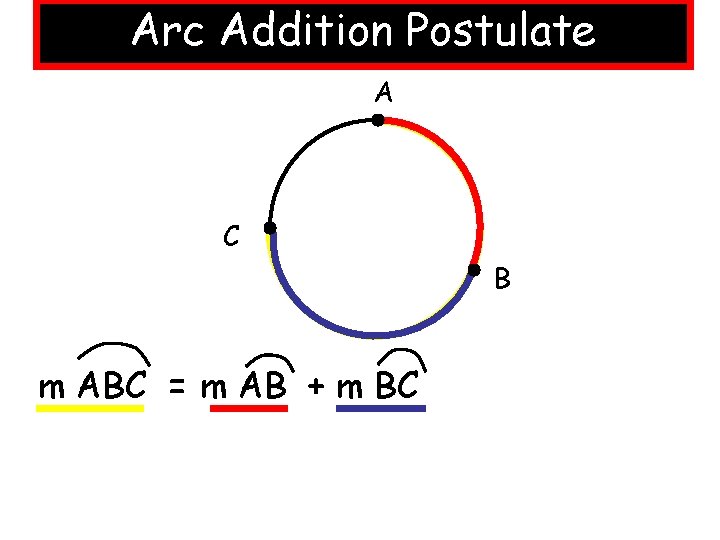
Arc Addition Postulate A C B m ABC = m AB + m BC

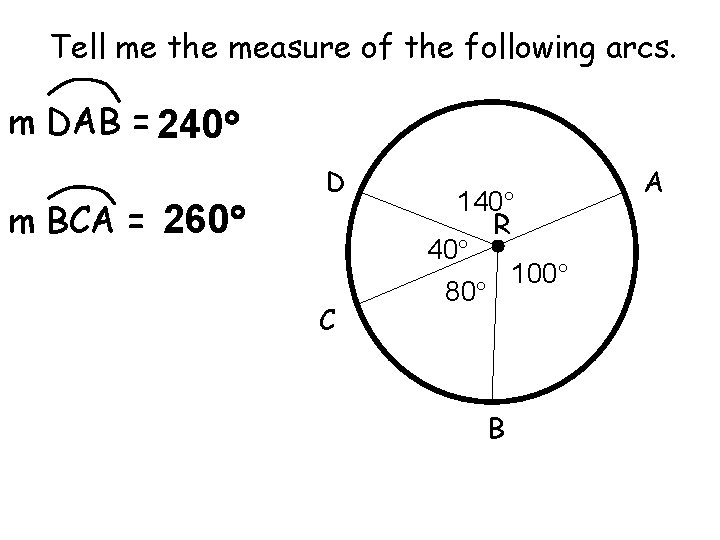
Tell me the measure of the following arcs. m DAB = 240 m BCA = 260 D C 140 R 40 100 80 B A

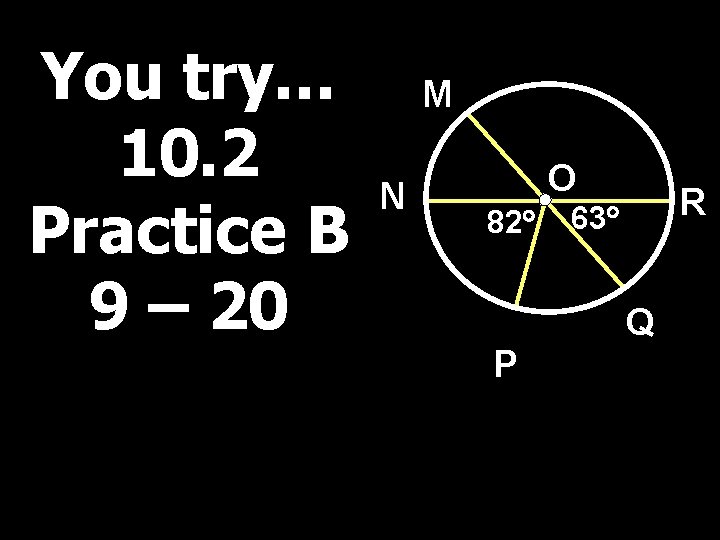
You try… 10. 2 Practice B 9 – 20 M N O 82 P R 63 Q

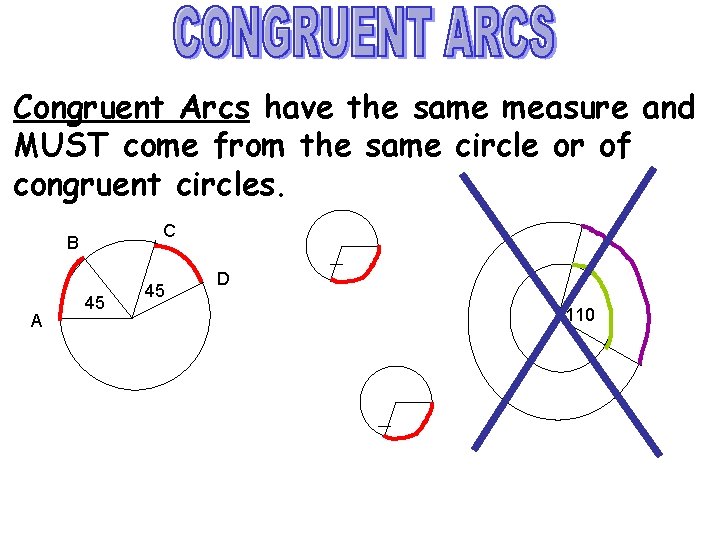
Congruent Arcs have the same measure and MUST come from the same circle or of congruent circles. C B A 45 45 D 110

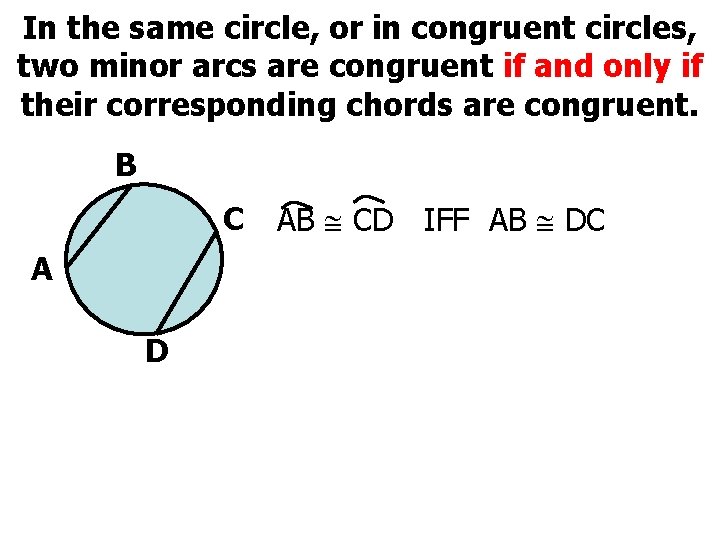
In the same circle, or in congruent circles, two minor arcs are congruent if and only if their corresponding chords are congruent. B C A D AB CD IFF AB DC

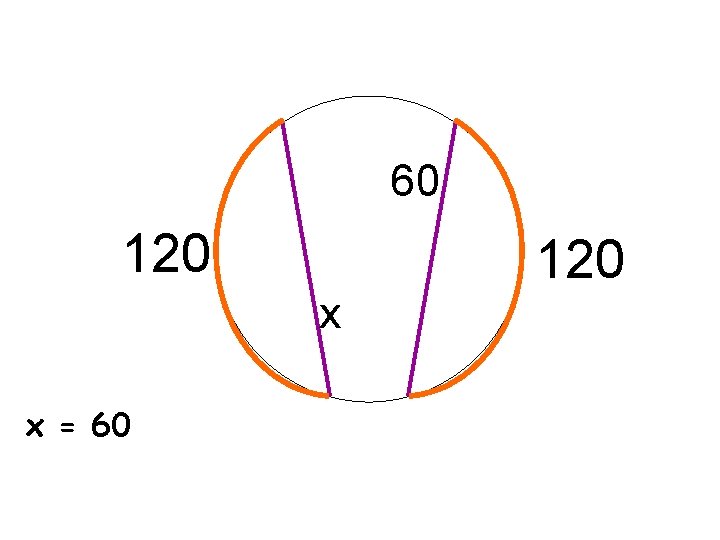
60 120 x x = 60 120

2 x 2 x = x + 40 x = 40 x + 40

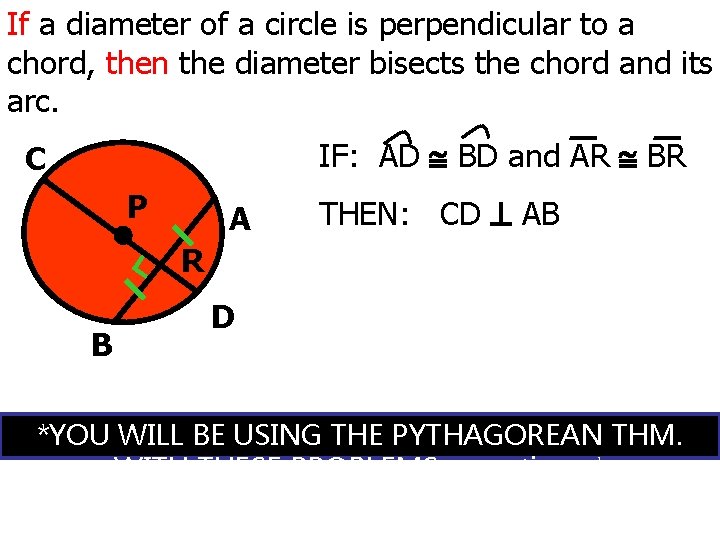
If a diameter of a circle is perpendicular to a chord, then the diameter bisects the chord and its arc. IF: AD BD and AR BR C P A THEN: CD AB R B D *YOU WILL BE USING THE PYTHAGOREAN THM. WITH THESE PROBLEMS sometimes*

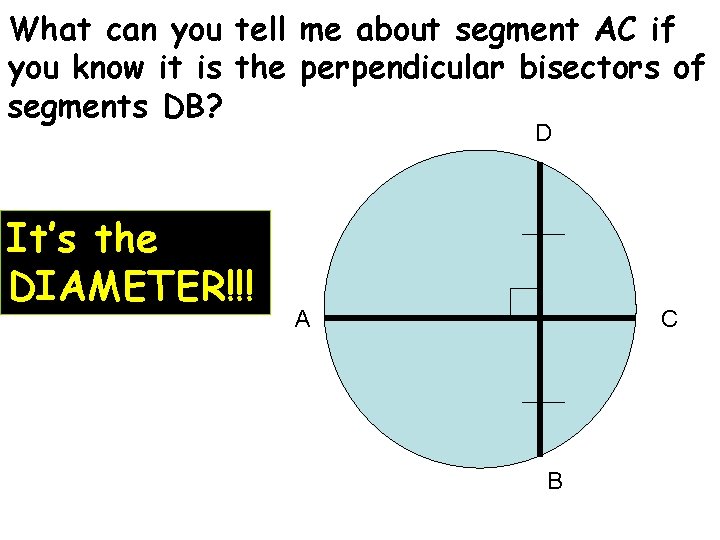
What can you tell me about segment AC if you know it is the perpendicular bisectors of segments DB? D It’s the DIAMETER!!! A C B

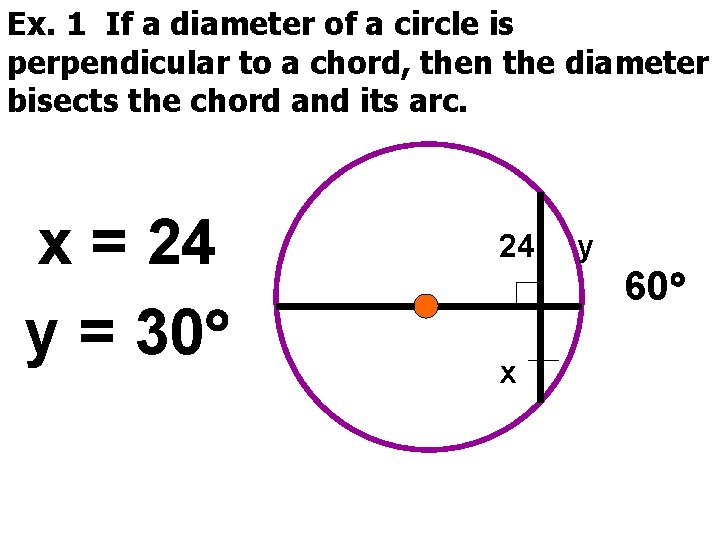
Ex. 1 If a diameter of a circle is perpendicular to a chord, then the diameter bisects the chord and its arc. x = 24 y = 30 24 y 60 x

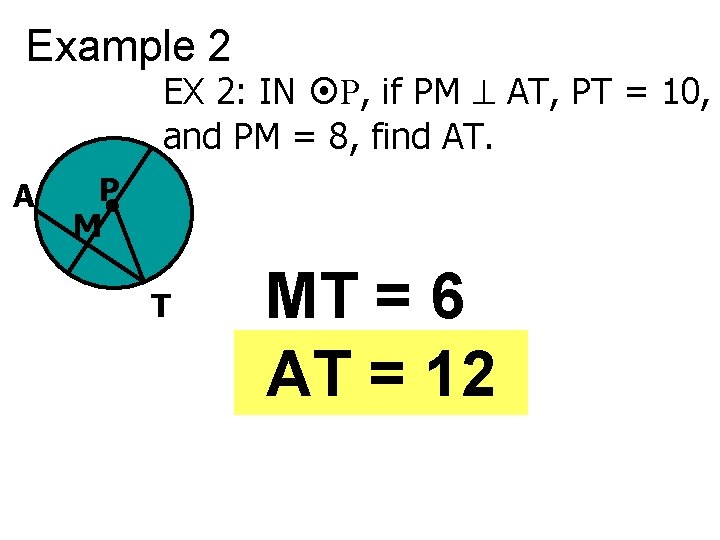
Example 2 EX 2: IN P, if PM AT, PT = 10, and PM = 8, find AT. A P M T MT = 6 AT = 12

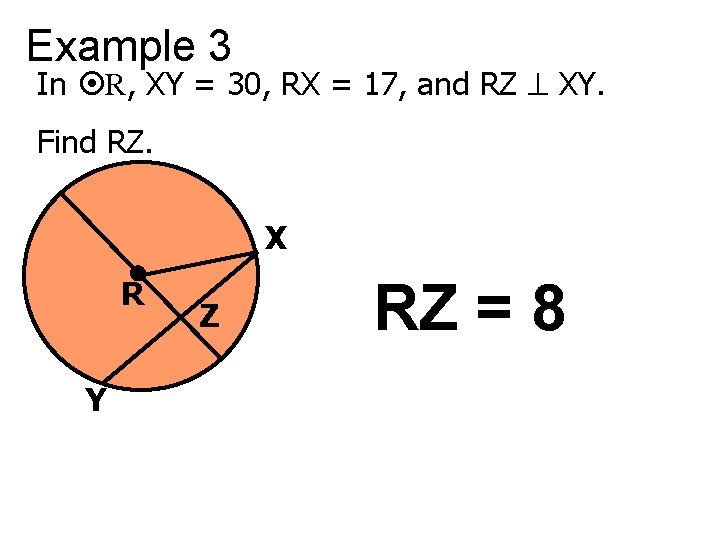
Example 3 In R, XY = 30, RX = 17, and RZ XY. Find RZ. X R Y Z RZ = 8

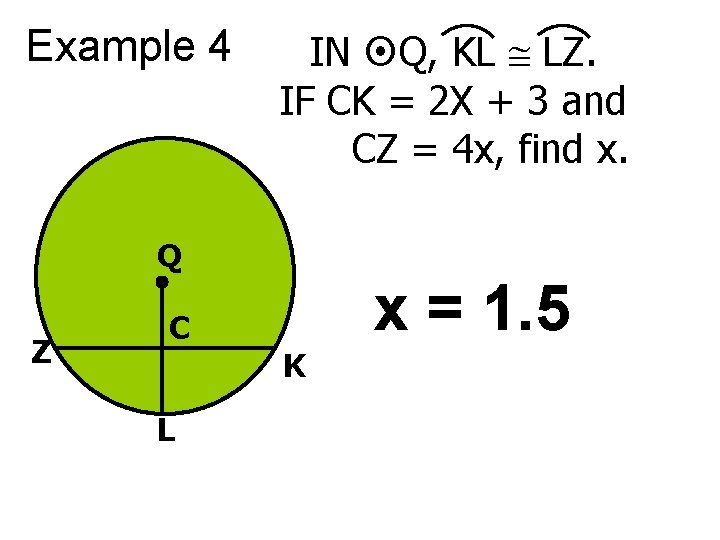
Example 4 IN Q, KL LZ. IF CK = 2 X + 3 and CZ = 4 x, find x. Q Z C L x = 1. 5 K

You try… 10. 2 Practice B 23 – 26

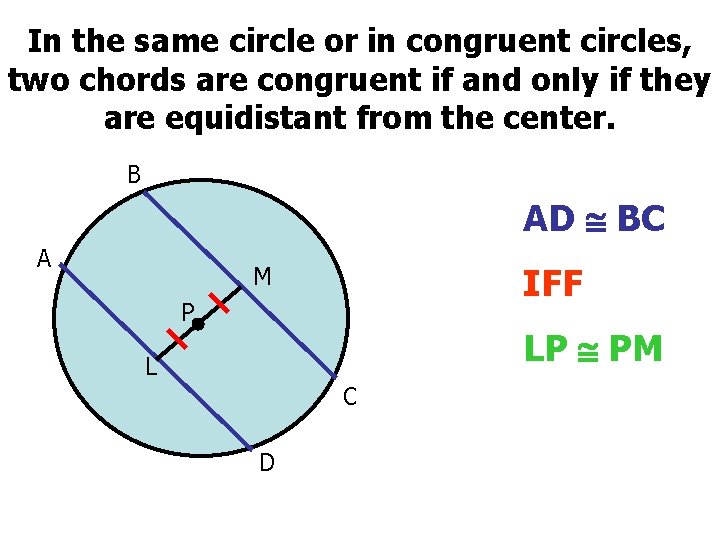
In the same circle or in congruent circles, two chords are congruent if and only if they are equidistant from the center. B AD BC A IFF M P LP PM L C D

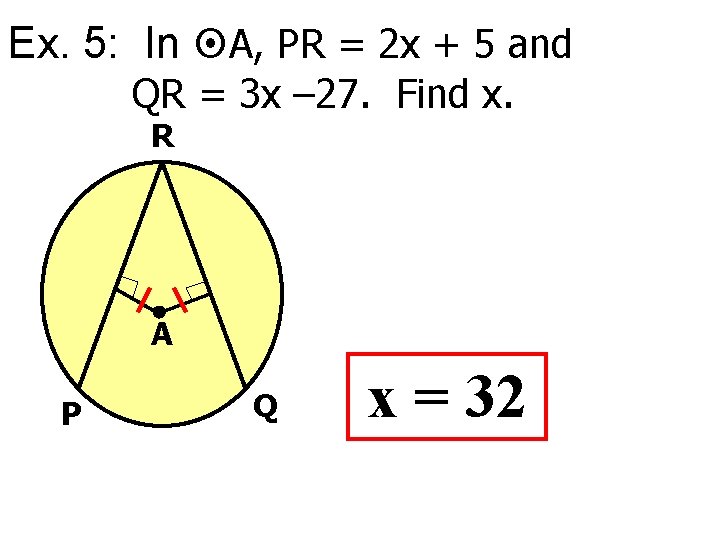
Ex. 5: In A, PR = 2 x + 5 and QR = 3 x – 27. Find x. R A P Q x = 32

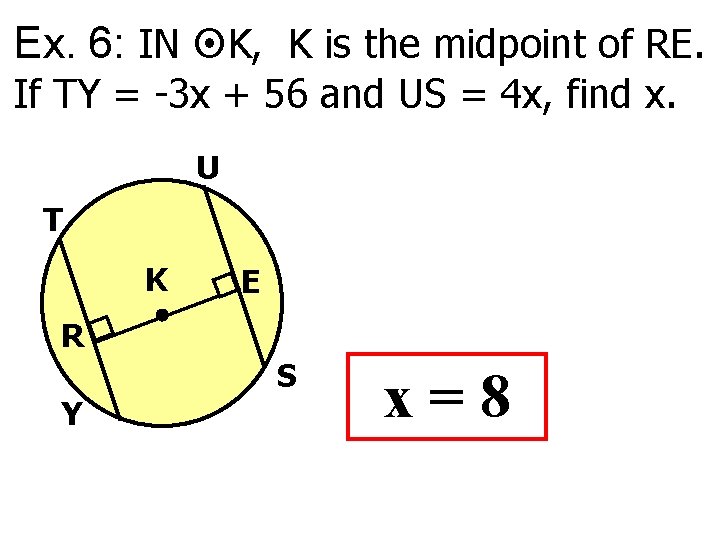
Ex. 6: IN K, K is the midpoint of RE. If TY = -3 x + 56 and US = 4 x, find x. U T K E R Y S x=8

Arcs & Chords Foldable

Practice: Finish practice work at home.