1 CSCI 104 2 3 Trees Mark Redekopp

1 CSCI 104 2 -3 Trees Mark Redekopp David Kempe

2 Properties, Insertion and Removal BINARY SEARCH TREES

3 Binary Search Tree • Binary search tree = binary tree where all nodes meet the property that: – All values of nodes in left subtree are less-than or equal than the parent’s value – All values of nodes in right subtree are greater-than or equal than the parent’s value 25 18 7 47 20 32 56 If we wanted to print the values in sorted order would you use an pre-order, in-order, or post-order traversal?

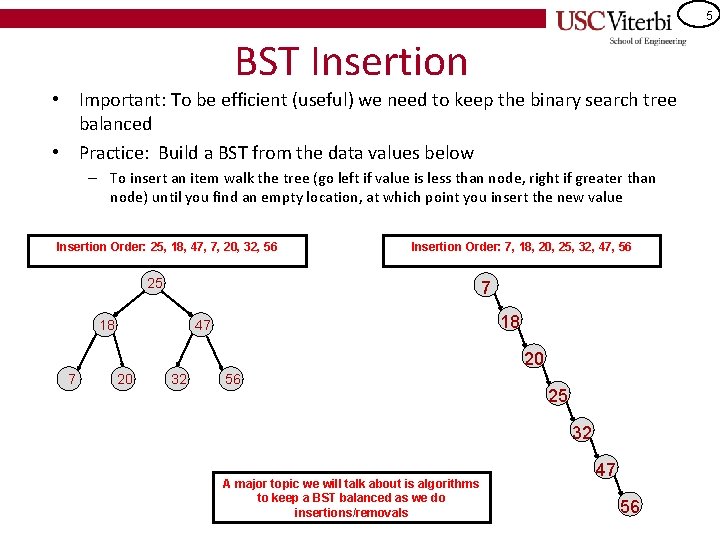
4 BST Insertion • Important: To be efficient (useful) we need to keep the binary search tree balanced • Practice: Build a BST from the data values below – To insert an item walk the tree (go left if value is less than node, right if greater than node) until you find an empty location, at which point you insert the new value Insertion Order: 25, 18, 47, 7, 20, 32, 56 Insertion Order: 7, 18, 20, 25, 32, 47, 56

5 BST Insertion • Important: To be efficient (useful) we need to keep the binary search tree balanced • Practice: Build a BST from the data values below – To insert an item walk the tree (go left if value is less than node, right if greater than node) until you find an empty location, at which point you insert the new value Insertion Order: 25, 18, 47, 7, 20, 32, 56 Insertion Order: 7, 18, 20, 25, 32, 47, 56 25 7 18 18 47 20 32 56 25 32 A major topic we will talk about is algorithms to keep a BST balanced as we do insertions/removals 47 56

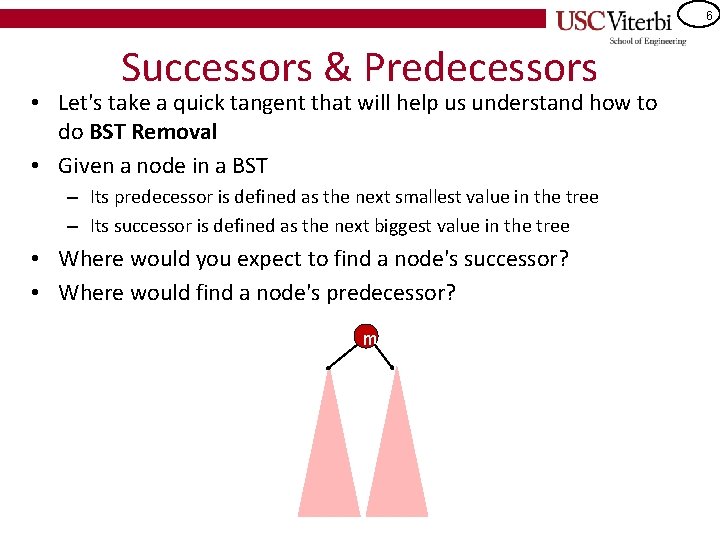
6 Successors & Predecessors • Let's take a quick tangent that will help us understand how to do BST Removal • Given a node in a BST – Its predecessor is defined as the next smallest value in the tree – Its successor is defined as the next biggest value in the tree • Where would you expect to find a node's successor? • Where would find a node's predecessor? m

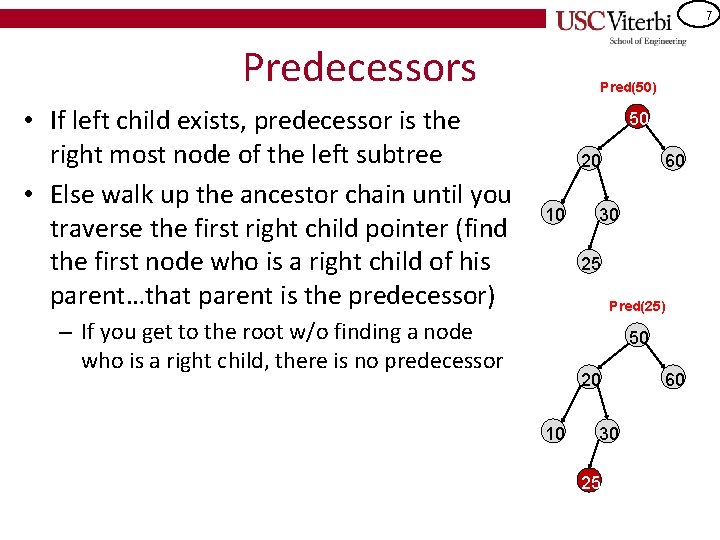
7 Predecessors • If left child exists, predecessor is the right most node of the left subtree • Else walk up the ancestor chain until you traverse the first right child pointer (find the first node who is a right child of his parent…that parent is the predecessor) Pred(50) 50 20 10 60 30 25 Pred(25) – If you get to the root w/o finding a node who is a right child, there is no predecessor 50 20 10 30 25 60

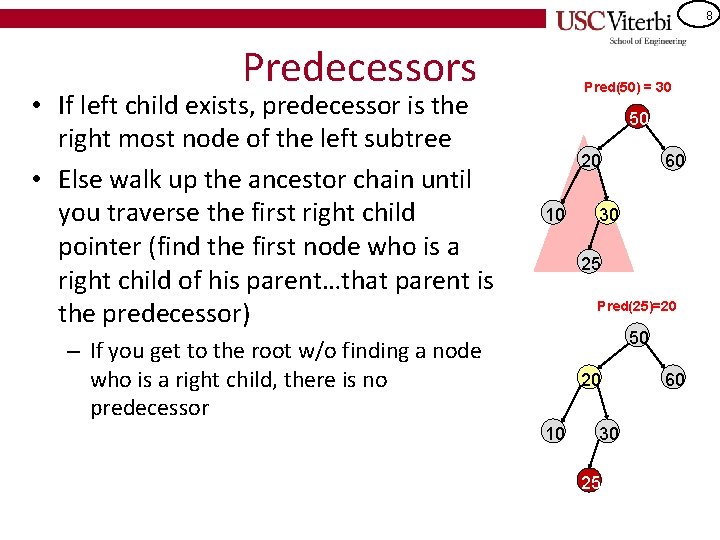
8 Predecessors • If left child exists, predecessor is the right most node of the left subtree • Else walk up the ancestor chain until you traverse the first right child pointer (find the first node who is a right child of his parent…that parent is the predecessor) Pred(50) = 30 50 20 10 60 30 25 Pred(25)=20 50 – If you get to the root w/o finding a node who is a right child, there is no predecessor 20 10 30 25 60

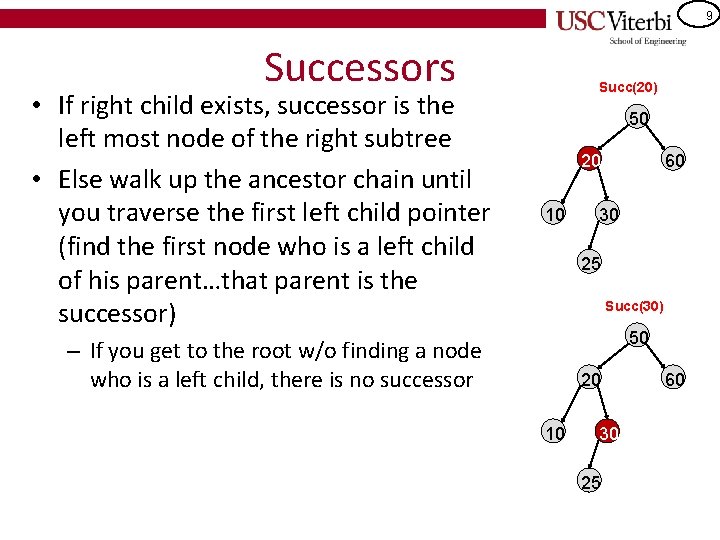
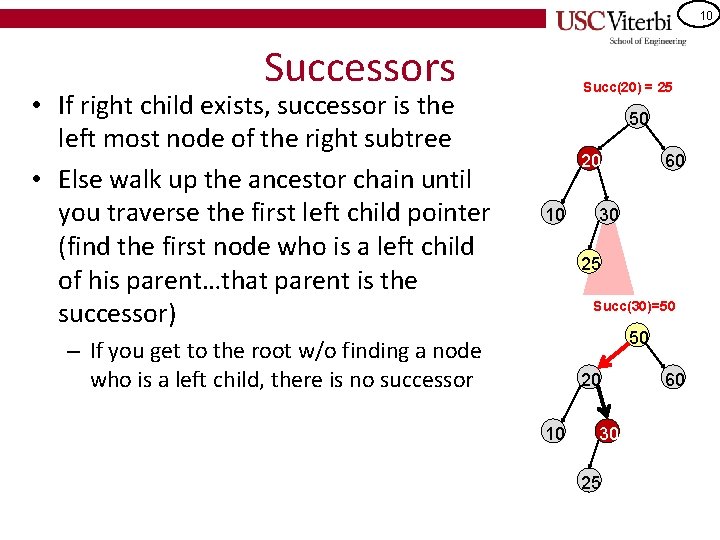
9 Successors • If right child exists, successor is the left most node of the right subtree • Else walk up the ancestor chain until you traverse the first left child pointer (find the first node who is a left child of his parent…that parent is the successor) Succ(20) 50 20 10 60 30 25 Succ(30) 50 – If you get to the root w/o finding a node who is a left child, there is no successor 20 10 30 25 60

10 Successors • If right child exists, successor is the left most node of the right subtree • Else walk up the ancestor chain until you traverse the first left child pointer (find the first node who is a left child of his parent…that parent is the successor) Succ(20) = 25 50 20 10 60 30 25 Succ(30)=50 50 – If you get to the root w/o finding a node who is a left child, there is no successor 20 10 30 25 60

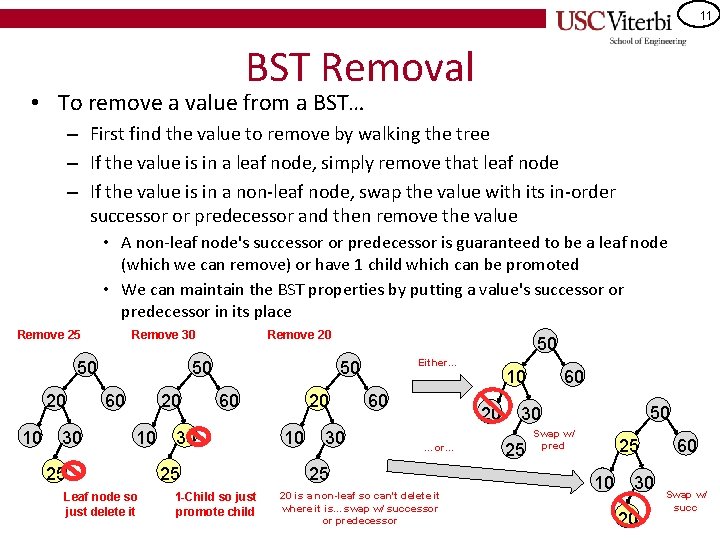
11 BST Removal • To remove a value from a BST… – First find the value to remove by walking the tree – If the value is in a leaf node, simply remove that leaf node – If the value is in a non-leaf node, swap the value with its in-order successor or predecessor and then remove the value • A non-leaf node's successor or predecessor is guaranteed to be a leaf node (which we can remove) or have 1 child which can be promoted • We can maintain the BST properties by putting a value's successor or predecessor in its place Remove 30 Remove 25 50 50 20 10 30 Remove 20 20 60 10 25 Leaf node so just delete it 50 Either… 50 60 30 25 1 -Child so just promote child 20 10 30 60 10 20 …or… 25 20 is a non-leaf so can't delete it where it is…swap w/ successor or predecessor 60 50 30 25 Swap w/ pred 25 10 30 20 60 Swap w/ succ

12 Worst Case BST Efficiency • Insertion – Balanced: _____ – Unbalanced: _____ • Removal – Balanced: ____ – Unbalanced: _____ • Find/Search – Balanced: _____ – Unbalanced: _____ #include<iostream> using namespace std; // Bin. Search Tree template <typename T> class BST { public: BTree(); ~BTree(); virtual bool empty() = 0; virtual void insert(const T& v) = 0; virtual void remove(const T& v) = 0; virtual T* find(const T& v) = 0; };

13 BST Efficiency • Insertion – Balanced: O(log n) – Unbalanced: O(n) • Removal – Balanced : O(log n) – Unbalanced: O(n) • Find/Search – Balanced : O(log n) – Unbalanced: O(n) #include<iostream> using namespace std; // Bin. Search Tree template <typename T> class BST { public: BTree(); ~BTree(); virtual bool empty() = 0; virtual void insert(const T& v) = 0; virtual void remove(const T& v) = 0; virtual T* find(const T& v) = 0; };

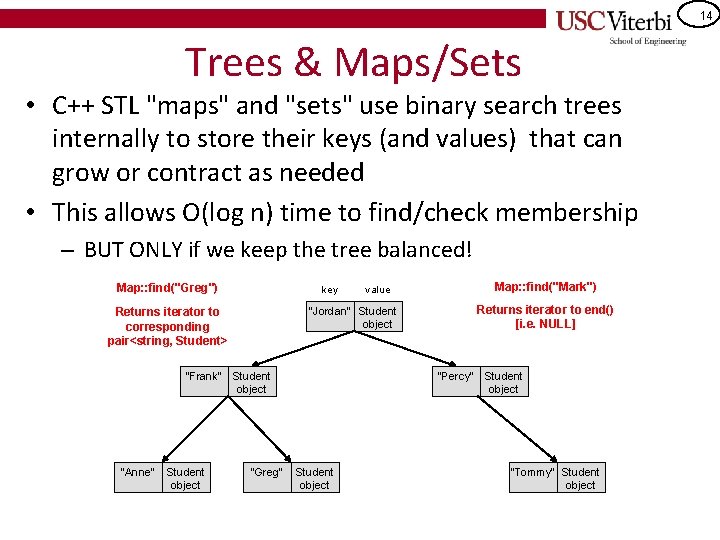
14 Trees & Maps/Sets • C++ STL "maps" and "sets" use binary search trees internally to store their keys (and values) that can grow or contract as needed • This allows O(log n) time to find/check membership – BUT ONLY if we keep the tree balanced! Map: : find("Greg") key "Anne" Student object Returns iterator to end() [i. e. NULL] "Jordan" Student object Returns iterator to corresponding pair<string, Student> "Frank" Map: : find("Mark") value Student object "Greg" "Percy" Student object "Tommy" Student object

15 An example of B-Trees 2 -3 TREES

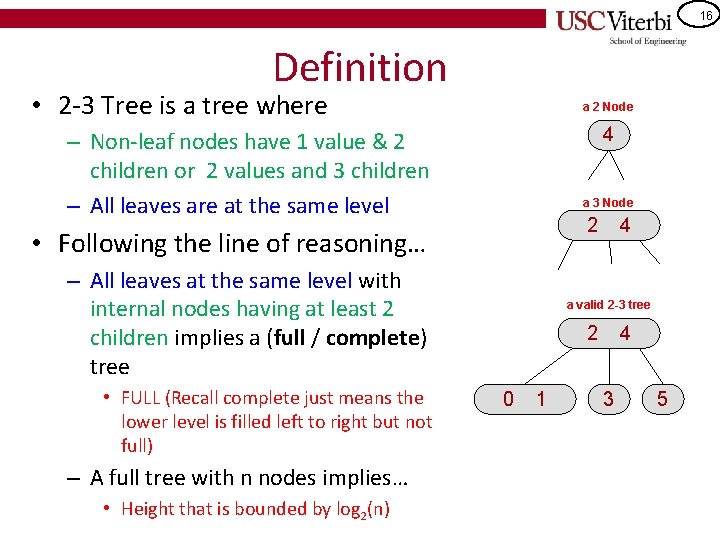
16 Definition • 2 -3 Tree is a tree where a 2 Node 4 – Non-leaf nodes have 1 value & 2 children or 2 values and 3 children – All leaves are at the same level a 3 Node 2 • Following the line of reasoning… – All leaves at the same level with internal nodes having at least 2 children implies a (full / complete) tree • FULL (Recall complete just means the lower level is filled left to right but not full) – A full tree with n nodes implies… • Height that is bounded by log 2(n) 4 a valid 2 -3 tree 2 0 1 4 3 5

17 Implementation of 2 - & 3 -Nodes • You will see that at different times 2 nodes may have to be upgraded to 3 nodes • To model these nodes we plan for the worst case…a 3 node • This requires wasted storage for 2 nodes template <typename T> struct Item 23 { T val 1; T val 2; Item 23<T>* left; Item 23<T>* mid; Item 23<T>* right; bool two. Node; }; a 2 Node _ a 3 Node _ _

18 2 -3 Search Trees • Similar properties as a BST • 2 -3 Search Tree – If a 2 Node with value, m a 2 Node • Left subtree nodes are < node value • Right subtree nodes are > node value a 3 Node m l r – If a 3 Node with value, l and r • Left subtree nodes are < l • Middle subtree > l and < r • Right subtree nodes are > r • 2 -3 Trees are almost always used as search trees, so from now on if we say 2 -3 tree we mean 2 -3 search tree < m > m m= "median" or "middle" < l >l && <r l = left r = right > r

19 2 -3 Search Tree • Binary search tree compared to 2 -3 tree • Check if 55 is in the tree? 20 10 30 25 BST 2 -3 Tree 50 20 30 60 10 25 50 60

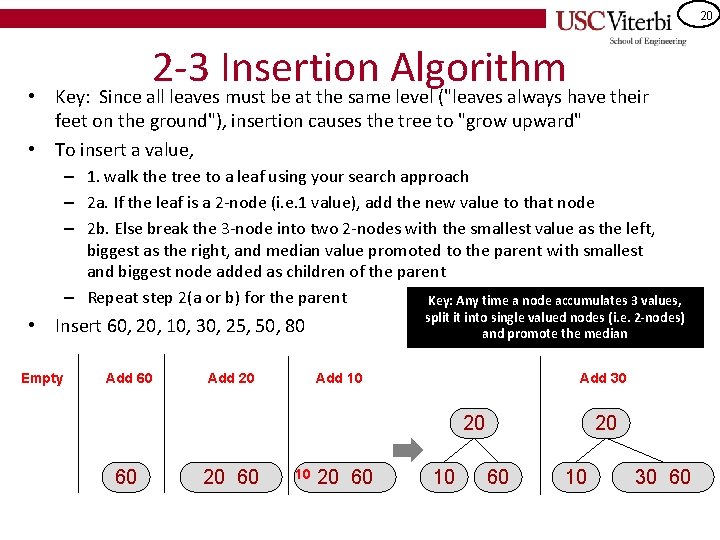
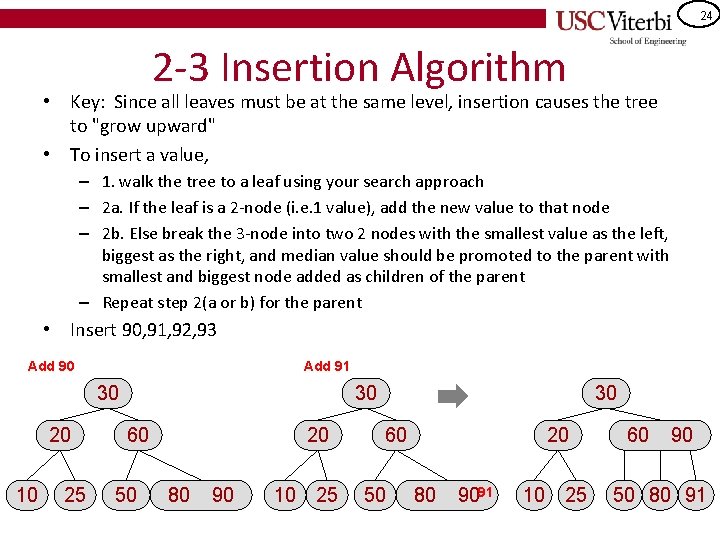
20 • 2 -3 Insertion Algorithm Key: Since all leaves must be at the same level ("leaves always have their feet on the ground"), insertion causes the tree to "grow upward" • To insert a value, – 1. walk the tree to a leaf using your search approach – 2 a. If the leaf is a 2 -node (i. e. 1 value), add the new value to that node – 2 b. Else break the 3 -node into two 2 -nodes with the smallest value as the left, biggest as the right, and median value promoted to the parent with smallest and biggest node added as children of the parent – Repeat step 2(a or b) for the parent Key: Any time a node accumulates 3 values, split it into single valued nodes (i. e. 2 -nodes) and promote the median • Insert 60, 20, 10, 30, 25, 50, 80 Empty Add 60 Add 20 Add 10 Add 30 20 60 10 30 60

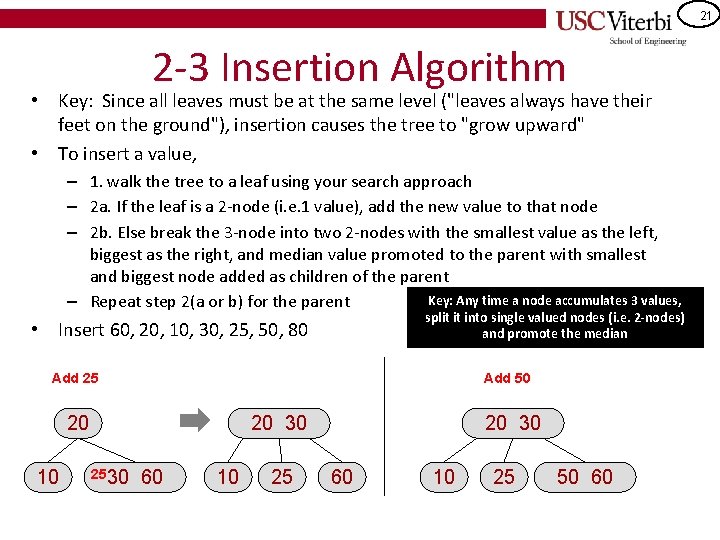
21 2 -3 Insertion Algorithm • Key: Since all leaves must be at the same level ("leaves always have their feet on the ground"), insertion causes the tree to "grow upward" • To insert a value, – 1. walk the tree to a leaf using your search approach – 2 a. If the leaf is a 2 -node (i. e. 1 value), add the new value to that node – 2 b. Else break the 3 -node into two 2 -nodes with the smallest value as the left, biggest as the right, and median value promoted to the parent with smallest and biggest node added as children of the parent Key: Any time a node accumulates 3 values, – Repeat step 2(a or b) for the parent split it into single valued nodes (i. e. 2 -nodes) and promote the median • Insert 60, 20, 10, 30, 25, 50, 80 Add 25 Add 50 20 10 20 30 2530 60 10 25 50 60

22 2 -3 Insertion Algorithm • Key: Since all leaves must be at the same level ("leaves always have their feet on the ground"), insertion causes the tree to "grow upward" • To insert a value, – 1. walk the tree to a leaf using your search approach – 2 a. If the leaf is a 2 -node (i. e. 1 value), add the new value to that node – 2 b. Else break the 3 -node into two 2 nodes with the smallest value as the left, biggest as the right, and median value promoted to the parent with smallest and biggest node added as children of the parent Key: Any time a node accumulates 3 values, – Repeat step 2(a or b) for the parent split it into single valued nodes (i. e. 2 -nodes) and promote the median • Insert 60, 20, 10, 30, 25, 50, 80 30 Add 80 20 30 10 25 20 30 50 6080 10 25 20 60 50 80 10 60 25 50 80

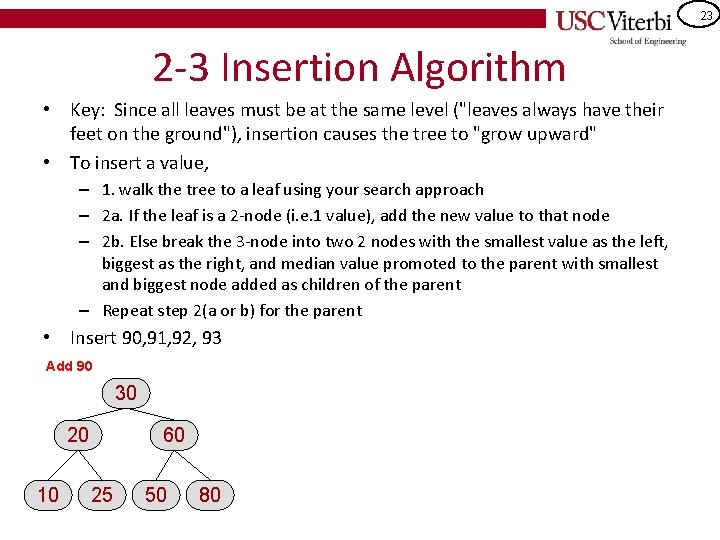
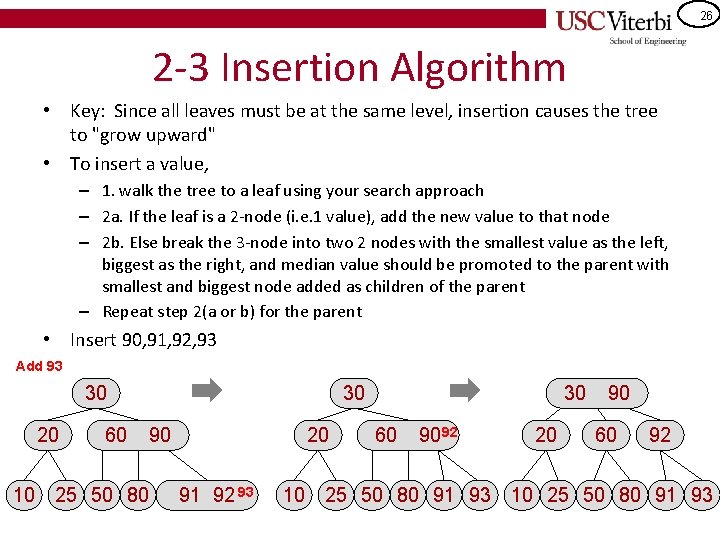
23 2 -3 Insertion Algorithm • Key: Since all leaves must be at the same level ("leaves always have their feet on the ground"), insertion causes the tree to "grow upward" • To insert a value, – 1. walk the tree to a leaf using your search approach – 2 a. If the leaf is a 2 -node (i. e. 1 value), add the new value to that node – 2 b. Else break the 3 -node into two 2 nodes with the smallest value as the left, biggest as the right, and median value promoted to the parent with smallest and biggest node added as children of the parent – Repeat step 2(a or b) for the parent • Insert 90, 91, 92, 93 Add 90 30 20 10 60 25 50 80

24 2 -3 Insertion Algorithm • Key: Since all leaves must be at the same level, insertion causes the tree to "grow upward" • To insert a value, – 1. walk the tree to a leaf using your search approach – 2 a. If the leaf is a 2 -node (i. e. 1 value), add the new value to that node – 2 b. Else break the 3 -node into two 2 nodes with the smallest value as the left, biggest as the right, and median value should be promoted to the parent with smallest and biggest node added as children of the parent – Repeat step 2(a or b) for the parent • Insert 90, 91, 92, 93 Add 90 Add 91 30 20 10 25 30 60 50 20 80 9091 10 25 60 90 50 80 91

25 2 -3 Insertion Algorithm • Key: Since all leaves must be at the same level, insertion causes the tree to "grow upward" • To insert a value, – 1. walk the tree to a leaf using your search approach – 2 a. If the leaf is a 2 -node (i. e. 1 value), add the new value to that node – 2 b. Else break the 3 -node into two 2 nodes with the smallest value as the left, biggest as the right, and median value should be promoted to the parent with smallest and biggest node added as children of the parent – Repeat step 2(a or b) for the parent • Insert 90, 91, 92, 93 Add 92 30 20 60 90 10 25 50 80 91 92

26 2 -3 Insertion Algorithm • Key: Since all leaves must be at the same level, insertion causes the tree to "grow upward" • To insert a value, – 1. walk the tree to a leaf using your search approach – 2 a. If the leaf is a 2 -node (i. e. 1 value), add the new value to that node – 2 b. Else break the 3 -node into two 2 nodes with the smallest value as the left, biggest as the right, and median value should be promoted to the parent with smallest and biggest node added as children of the parent – Repeat step 2(a or b) for the parent • Insert 90, 91, 92, 93 Add 93 30 20 60 30 90 10 25 50 80 20 91 92 93 30 60 90 92 20 90 60 92 10 25 50 80 91 93

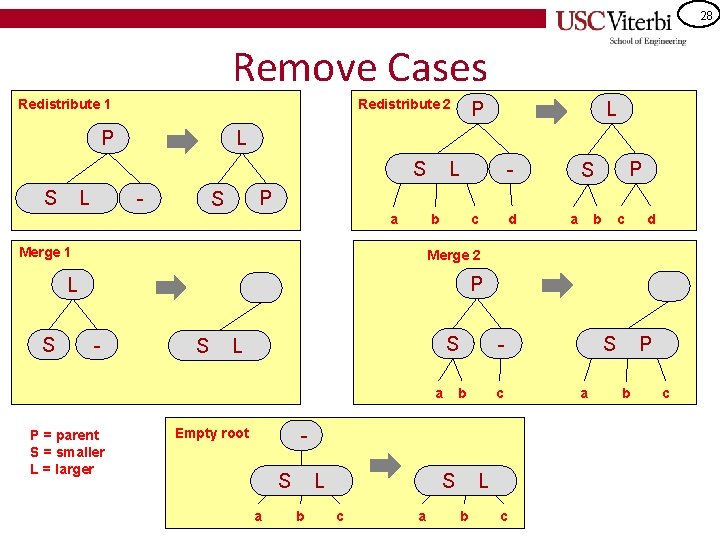
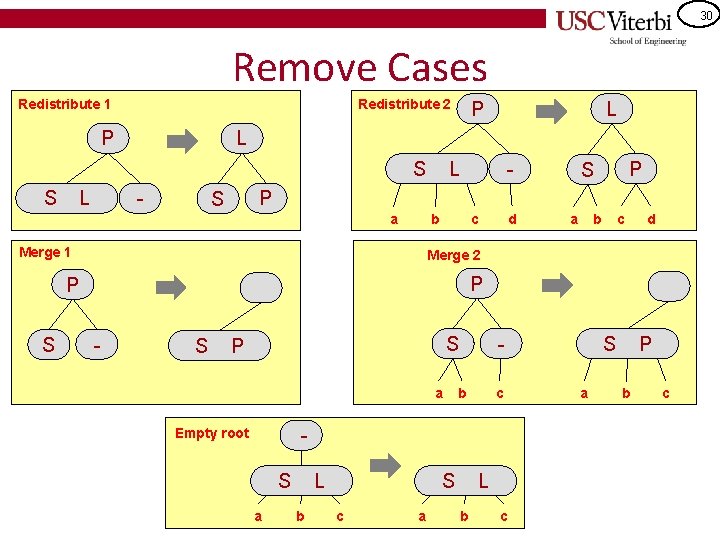
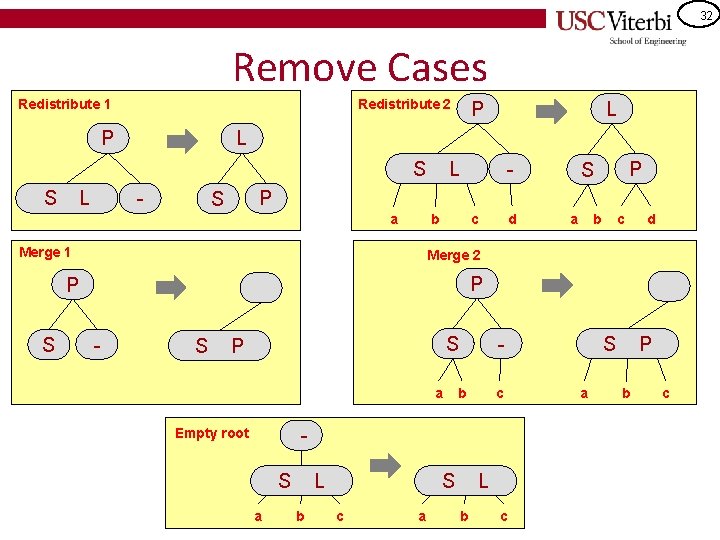
27 2 -3 Tree Removal Key: 2 -3 Trees must remain "full" (leaf nodes all at the same level) • • Remove Another key: Want to get item to remove down to a leaf and then work up the tree – 1. Find data item to remove – 2. If data item is not in a leaf node, find in-order successor (which is in a leaf node) and swap values (it's safe to put successor in your location) – 3. Remove item from the leaf node – 4. If leaf node is now empty, call fix. Tree(leaf. Node) • fix. Tree(n) – If n is root, delete root and return – Let p be the parent of n – If a sibling of n has two items • Redistribute items between n, sibling, and p and move any appropriate child from sibling to n – Else • Choose a sibling, s, of n and bring an item from p into s redistributing any children of n to s • Remove node n • If parent is empty, fix. Tree(p)

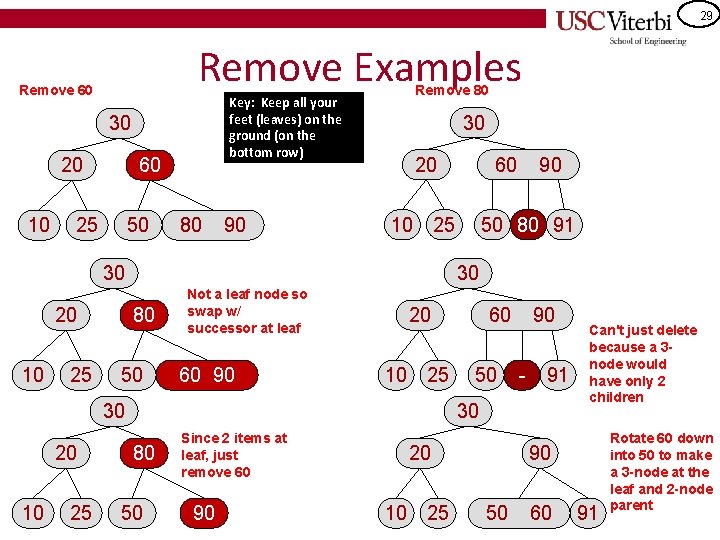
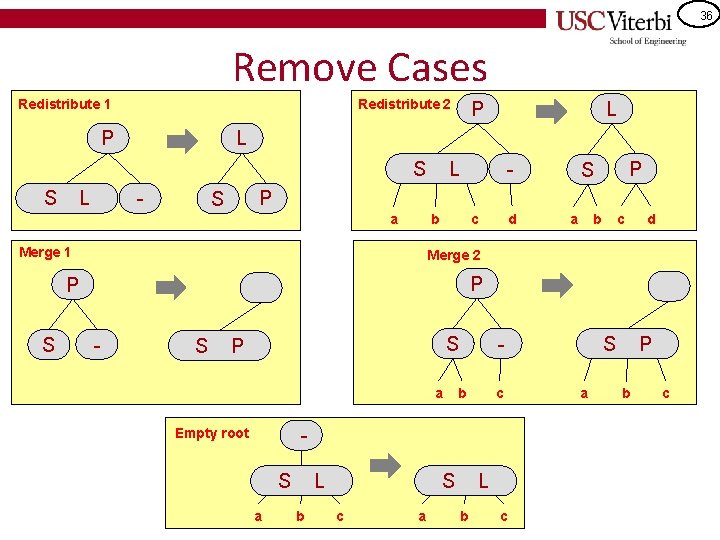
28 Remove Cases Redistribute 1 Redistribute 2 P L - P S a b Merge 1 c d a b c d Merge 2 P L S L L S S P - S a P = parent S = smaller L = larger - S L b c - Empty root S a S L b c a L b c S a P b c

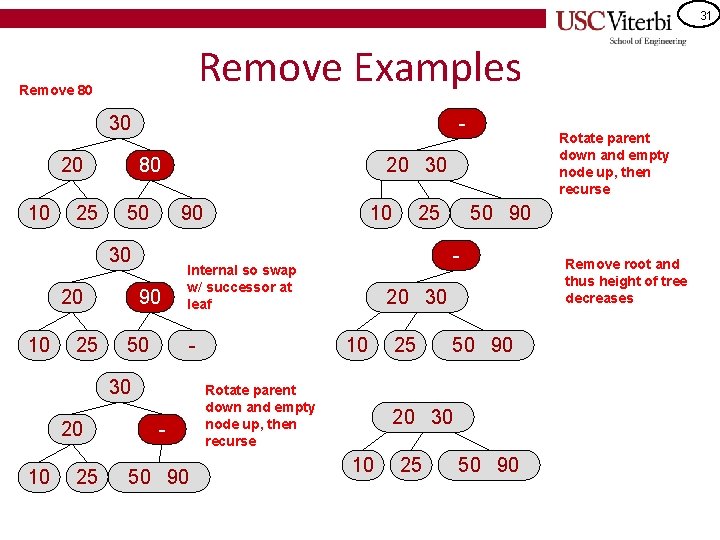
29 Remove Examples Remove 60 Key: Keep all your feet (leaves) on the ground (on the bottom row) 30 20 10 60 25 50 80 90 Remove 80 30 20 10 25 90 50 80 91 30 80 50 Not a leaf node so swap w/ successor at leaf 60 90 20 10 25 30 20 60 60 50 90 - 91 30 80 50 Since 2 items at leaf, just remove 60 90 20 10 25 Can't just delete because a 3 node would have only 2 children 90 50 60 91 Rotate 60 down into 50 to make a 3 -node at the leaf and 2 -node parent

30 Remove Cases Redistribute 1 Redistribute 2 P L - P S a b Merge 1 c d a b c d Merge 2 P P S L L S S P - S P a b c - Empty root S a S L b c a L b c S a P b c

31 Remove Examples Remove 80 30 20 10 25 80 50 20 10 25 20 30 90 50 10 25 10 - 50 90 25 50 90 - Internal so swap w/ successor at leaf 30 20 Rotate parent down and empty node up, then recurse 20 30 10 Rotate parent down and empty node up, then recurse 25 50 90 20 30 10 25 50 90 Remove root and thus height of tree decreases

32 Remove Cases Redistribute 1 Redistribute 2 P L - P S a b Merge 1 c d a b c d Merge 2 P P S L L S S P - S P a b c - Empty root S a S L b c a L b c S a P b c

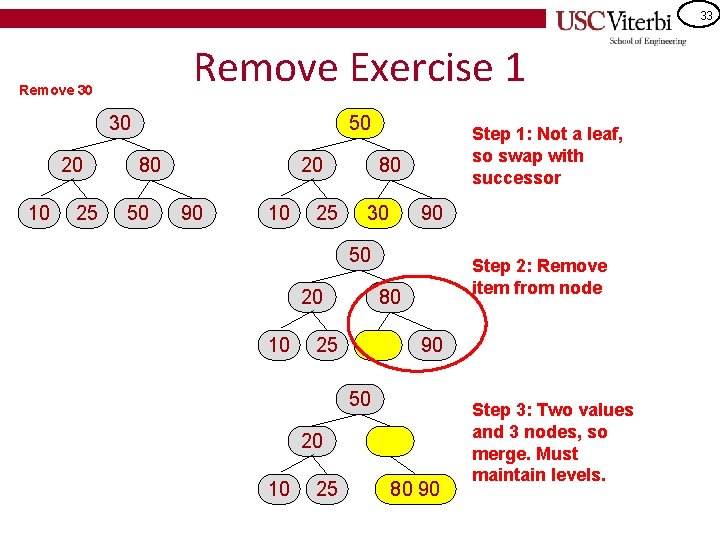
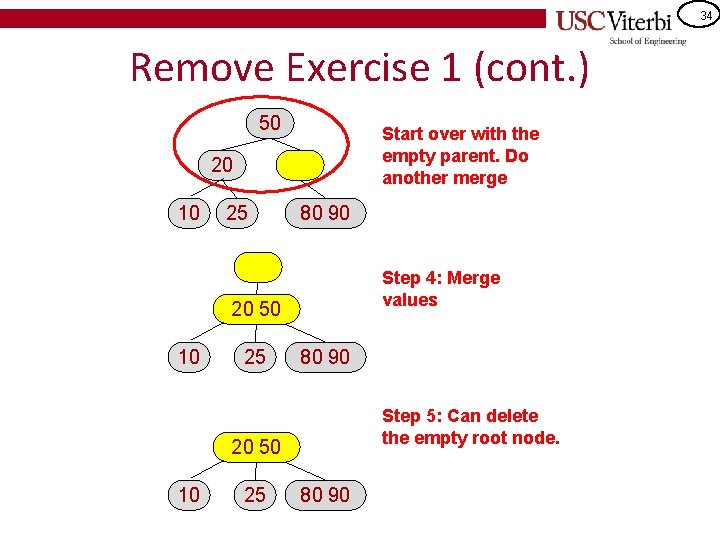
33 Remove Exercise 1 Remove 30 30 20 10 25 50 80 50 20 90 10 25 Step 1: Not a leaf, so swap with successor 80 30 90 50 20 10 Step 2: Remove item from node 80 25 90 50 20 10 25 80 90 Step 3: Two values and 3 nodes, so merge. Must maintain levels.

34 Remove Exercise 1 (cont. ) 50 Start over with the empty parent. Do another merge 20 10 25 80 90 Step 4: Merge values 20 50 10 25 80 90 Step 5: Can delete the empty root node. 20 50 10 25 80 90

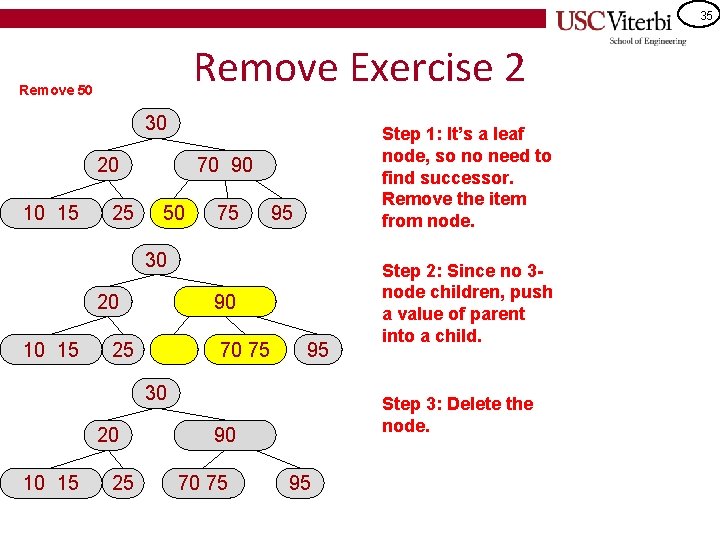
35 Remove Exercise 2 Remove 50 30 20 10 15 25 Step 1: It’s a leaf node, so no need to find successor. Remove the item from node. 70 90 50 75 95 30 20 10 15 90 25 70 75 95 30 20 10 15 25 Step 3: Delete the node. 90 70 75 Step 2: Since no 3 node children, push a value of parent into a child. 95

36 Remove Cases Redistribute 1 Redistribute 2 P L - P S a b Merge 1 c d a b c d Merge 2 P P S L L S S P - S P a b c - Empty root S a S L b c a L b c S a P b c

37 Insert 12 30 20 10 15 25 Insertion Exercise 1 70 90 50 75 95

38 Insert 23 35 Insertion Exercise 2 20 10 15 70 90 25 30 50 75 95

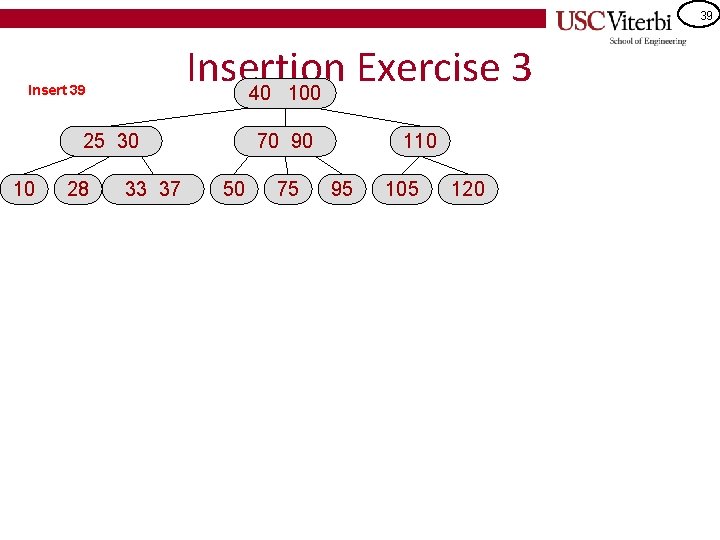
39 Insertion Exercise 3 40 100 Insert 39 25 30 10 28 33 37 70 90 50 75 110 95 105 120

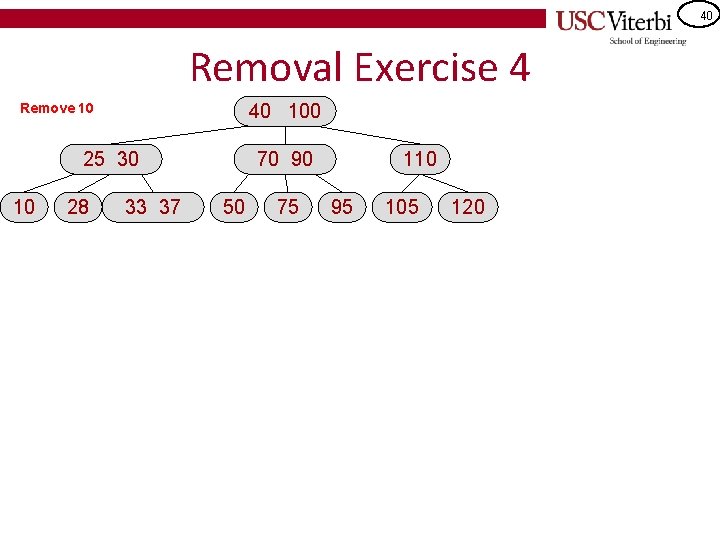
40 Removal Exercise 4 40 100 Remove 10 25 30 10 28 33 37 70 90 50 75 110 95 105 120

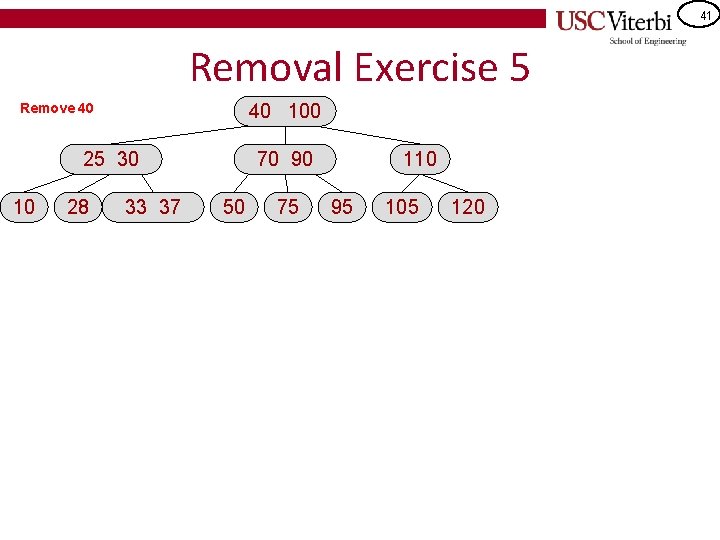
41 Removal Exercise 5 40 100 Remove 40 25 30 10 28 33 37 70 90 50 75 110 95 105 120

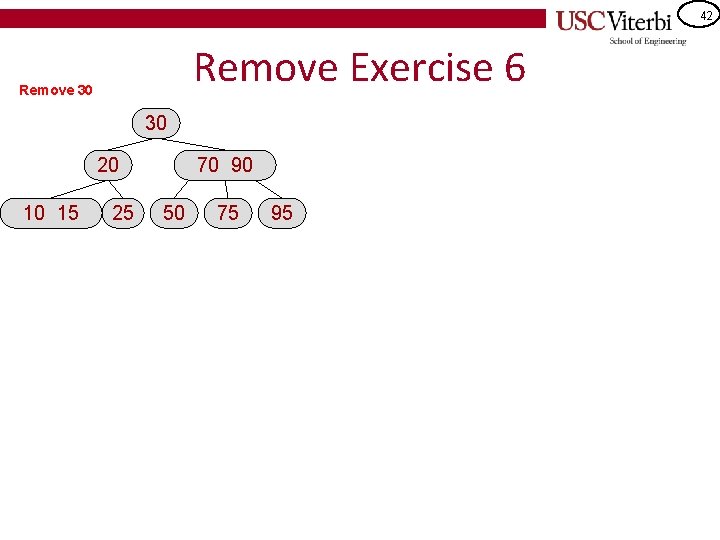
42 Remove Exercise 6 Remove 30 30 20 10 15 25 70 90 50 75 95

43 Other Resources • http: //www. cs. usfca. edu/~galles/visualization /BTree. html