1 Comp Sci 105 SS 2005 Principles of

1 Comp. Sci 105 SS 2005 Principles of Computer Science Test Tomorrow. Lecture 16: Searching and Sorting (Thursday) Lecturer: Santokh Singh

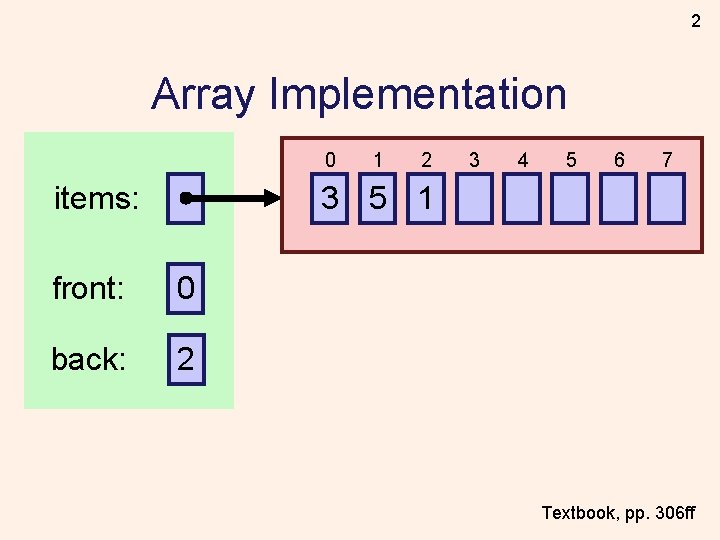
2 Array Implementation 0 items: 1 2 3 4 5 6 7 3 5 1 front: 0 back: 2 Textbook, pp. 306 ff

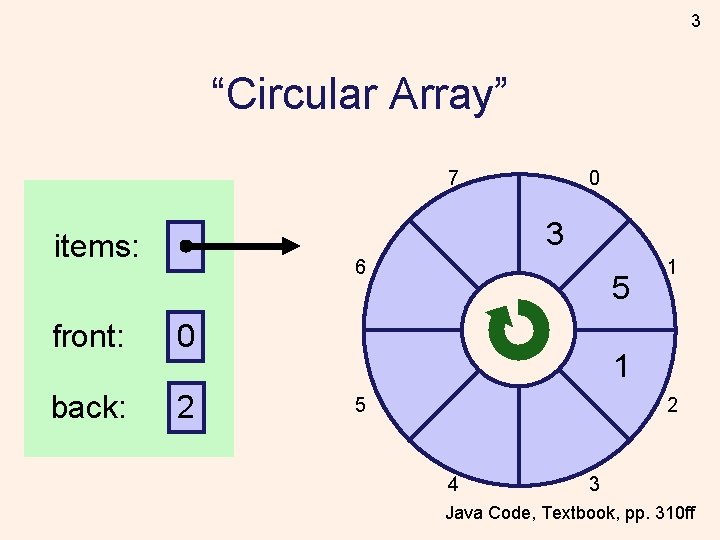
3 “Circular Array” 7 0 3 items: 6 front: 0 back: 2 5 1 1 5 2 4 3 Java Code, Textbook, pp. 310 ff

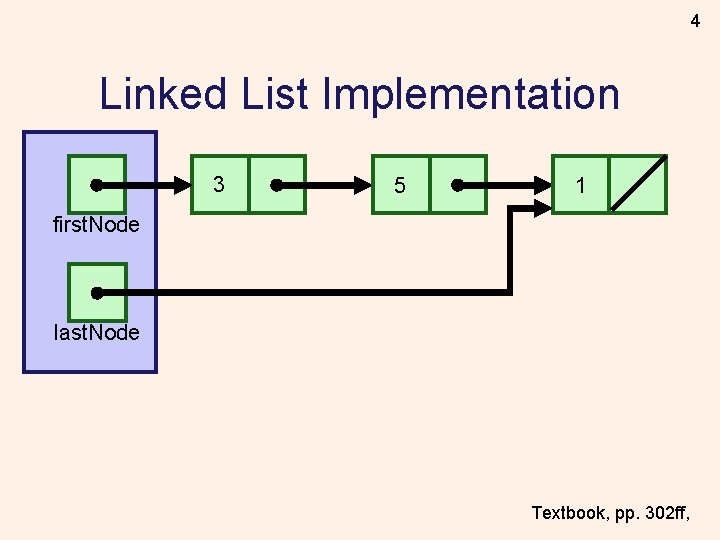
4 Linked List Implementation 3 5 1 first. Node last. Node Textbook, pp. 302 ff,

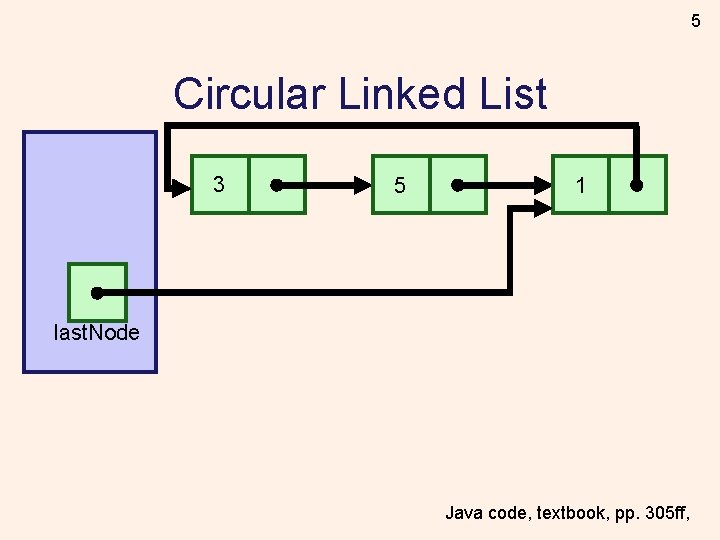
5 Circular Linked List 3 5 1 last. Node Java code, textbook, pp. 305 ff,

6 ADT List Implementation 1. 2. 3. 4. 5. 6. 1 5 3 Java Code, Textbook, pp. 263 ff

7 Algorithm Efficiency Challenges in Measuring Efficiency Counting Operations Growth Rates of Functions Big O Notation Examples General Rules

8 Algorithm Efficiency Challenges in Measuring Efficiency Counting Operations Growth Rates of Functions Big O Notation Examples General Rules

9 Node curr = head; while (curr != null ) { System. out. println( curr. get. Item() ); curr = curr. get. Next(); } Textbook, p. 374

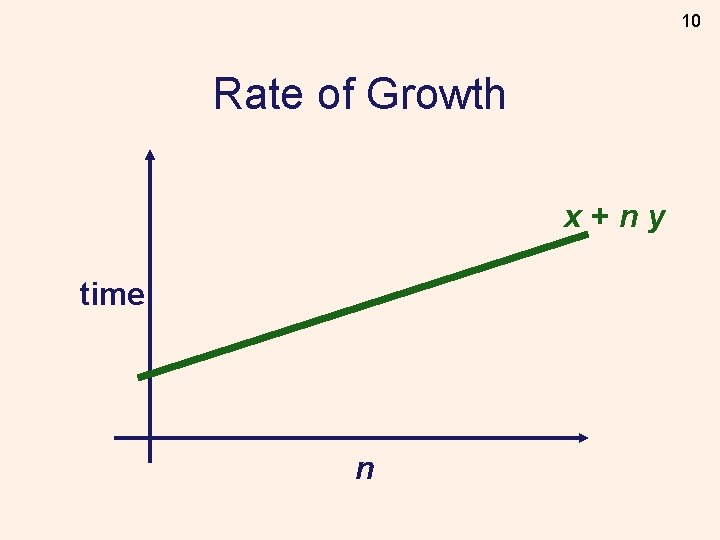
10 Rate of Growth x+ny time n

11 for ( i=1 to n ) { for ( j=1 to n ) { for ( k=1 to 5 ) { Task T } } }

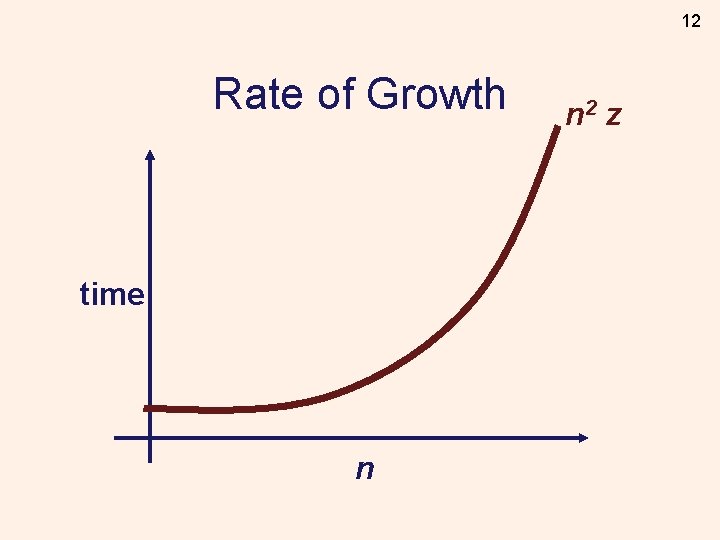
12 Rate of Growth time n n 2 z

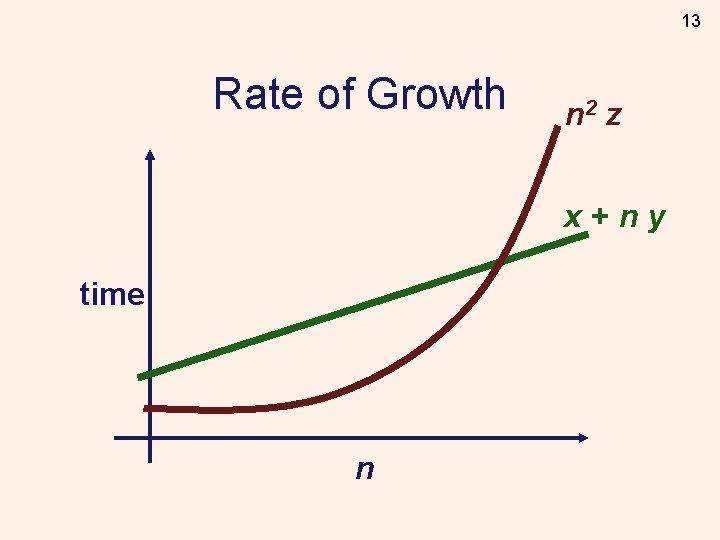
13 Rate of Growth n 2 z x+ny time n

14 Algorithm Efficiency Challenges in Measuring Efficiency Counting Operations Growth Rates of Functions Big O Notation Examples General Rules

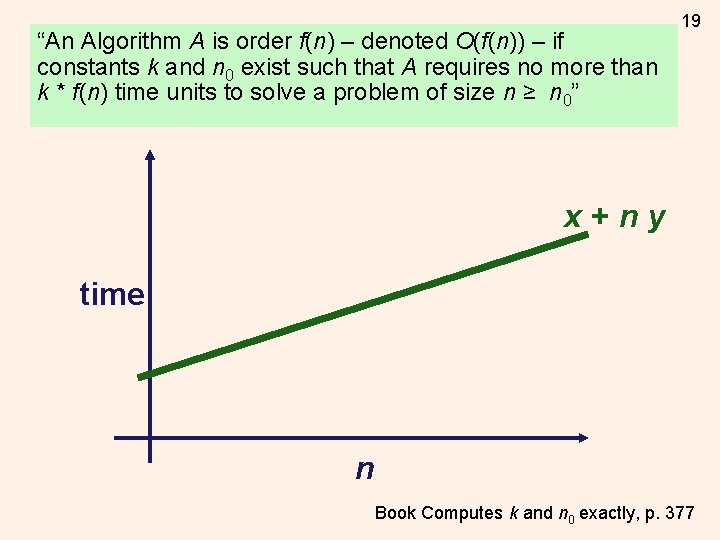
15 Big O Notation “An Algorithm A is order f(n) – denoted O(f(n)) – if constants k and n 0 exist such that A requires no more than k * f(n) time units to solve a problem of size n ≥ n 0” - Textbook, p. 376

16 Big O Notation “An Algorithm A is order f(n) – denoted O(f(n)) – if constants k and n 0 exist such that A requires no more than k * f(n) time units to solve a problem of size n ≥ n 0” - Textbook, p. 376

17 Big O Notation “An Algorithm A is order f(n) – denoted O(f(n)) – if constants k and n 0 exist such that A requires no more than k * f(n) time units to solve a problem of size n ≥ n 0” - Textbook, p. 376 Worst Case

18 Big O Notation “An Algorithm A is order f(n) – denoted O(f(n)) – if constants k and n 0 exist such that A requires no more than k * f(n) time units to solve a problem of size n ≥ n 0” - Textbook, p. 376 Worst Case Large Problems

“An Algorithm A is order f(n) – denoted O(f(n)) – if constants k and n 0 exist such that A requires no more than k * f(n) time units to solve a problem of size n ≥ n 0” Rate of Growth 19 n 2 z x+ny time n Book Computes k and n 0 exactly, p. 377

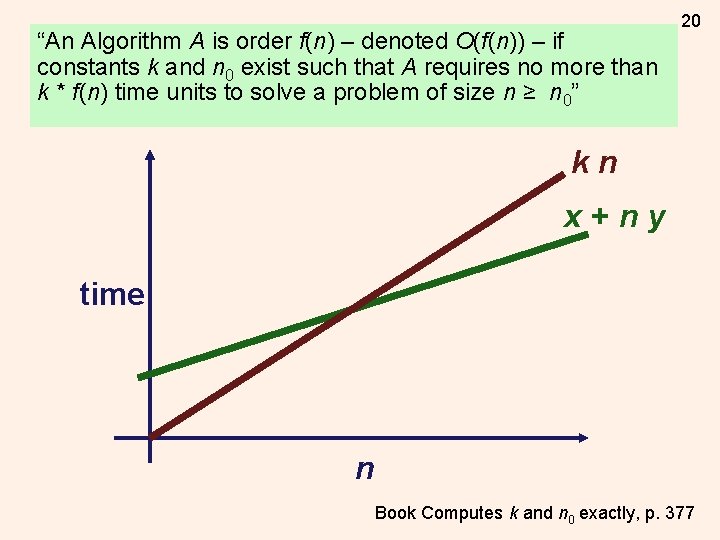
“An Algorithm A is order f(n) – denoted O(f(n)) – if constants k and n 0 exist such that A requires no more than k * f(n) time units to solve a problem of size n ≥ n 0” Rate of Growth 20 n 2 z kn x+ny time n Book Computes k and n 0 exactly, p. 377

21 for ( i=1 to n ) { for ( j=1 to n ) { for ( k=1 to 5 ) { Task T } } }

22 for ( i=1 to n ) { for ( j=1 to i ) { for ( k=1 to 5 ) { Task T } } } Textbook, p. 374 -5, 377

23 O Notation Tricks • Ignore “low-order” terms • Ignore Constants • Can combine O()’s Textbook, p. 380

24 Comparing Growth Rates O(n 2) Faster Growth O(n) Faster Code Textbook, p. 378

25 Comparing Growth Rates O(n 2) Faster Growth O(n) Faster Code O(1) Textbook, p. 378

26 Comparing Growth Rates O(2 n) O(n 2) Faster Growth O(n) Faster Code O(log n) O(1) Textbook, p. 378

27 Comparing Growth Rates O(2 n) O(n 3) O(n 2) Faster Growth O(n log n) O(n) Faster Code O(log n) O(1) Textbook, p. 378